Basic introduction to heap

Heap is a special kind of data structure in computer science.
Heap is usually an array object that can be regarded as a complete binary tree. All its elements are stored in a one-dimensional array in the order of a complete binary tree, and the value of any parent node must be less than or equal to (greater than or equal to) the value of the child node.

Two properties of heap:

• The value of a node in the heap is always not greater than or less than the value of its parent node
• Heap is always a complete binary tree.

Classification of heap:

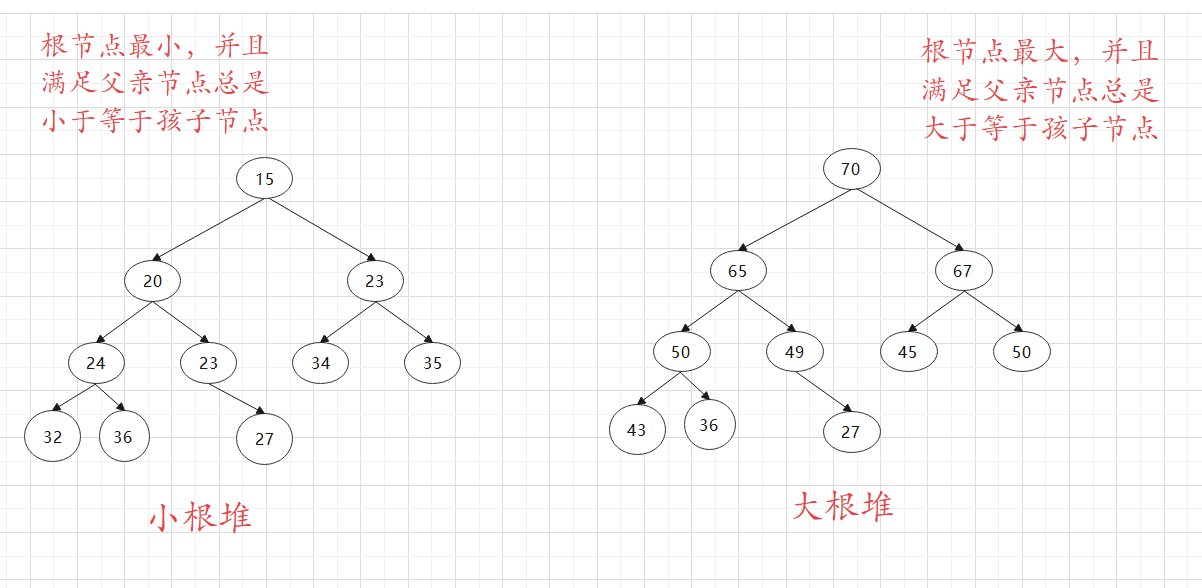
• Small root heap (small heap): the heap with the smallest root node
• Large root heap (large heap): the heap with the largest root node

Implementation of heap sorting

Since it is heap sorting, we must build a heap and sort based on the heap.

So the first thing is to build a heap. How can we make a pile of disordered numbers form a heap?

First of all, we need to understand the basic algorithm of heap sorting - downward adjustment algorithm

Heap building (downward adjustment algorithm)

First, we give an array, which is logically regarded as a complete binary tree.
int array[] = {27,15,19,18,28,34,65,49,25,37};

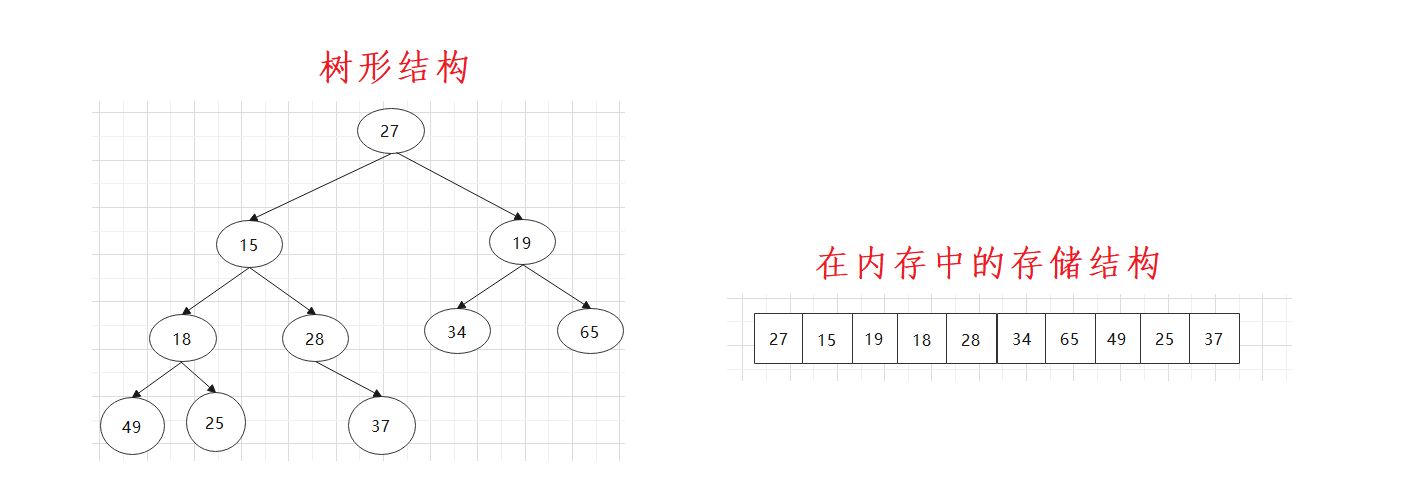
This is a special set of data, but this set of data just meets the conditions of downward adjustment algorithm

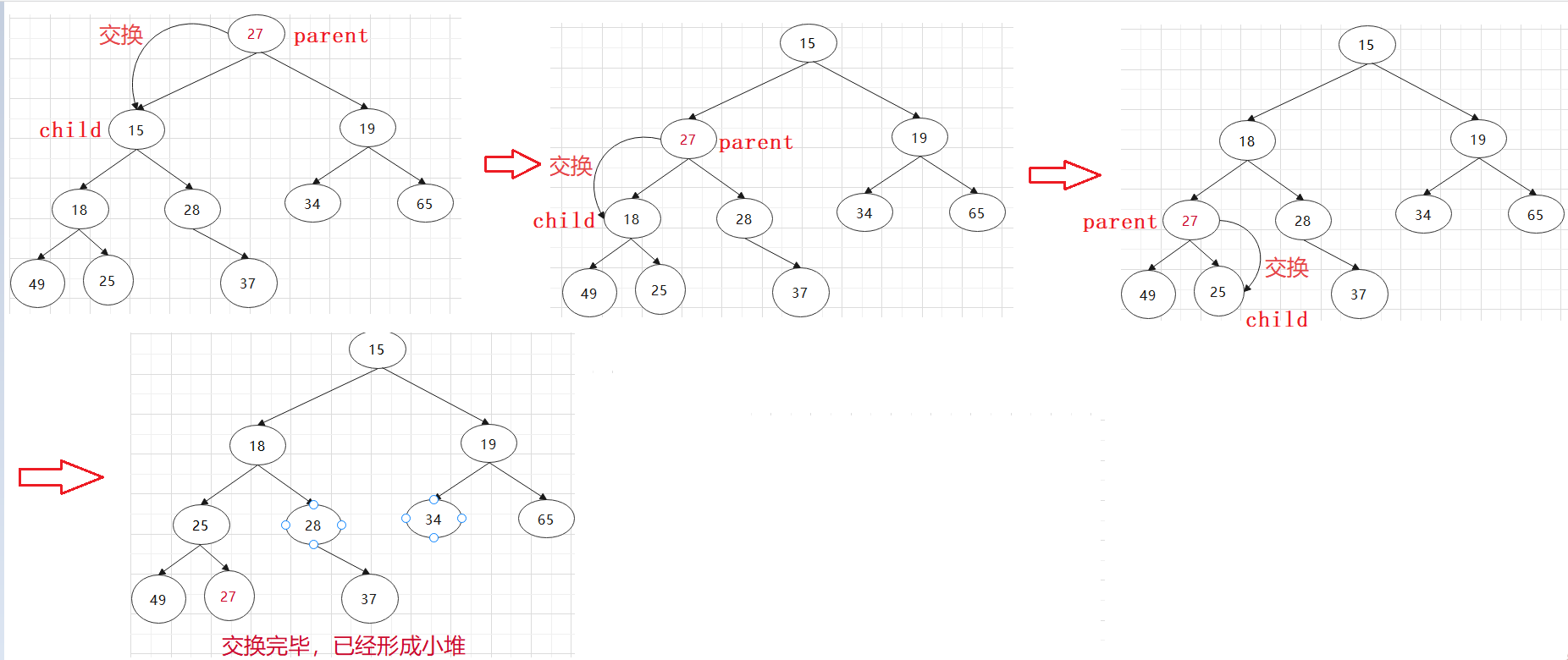
The downward adjustment algorithm has a premise: the left and right subtrees must be a heap before adjustment.

We can adjust it into a small heap through the downward adjustment algorithm starting from the root node.

By observing the data, we can find that only the data of the root node does not meet the small heap, but the left and right subtrees do. Therefore, we need to adjust step by step from the root node to form a small heap.

The adjustment is based on the small heap condition: any parent node is less than or equal to the child node.

Downward adjustment algorithm:

1. Start from the root node and adjust downward
2. Choose the younger of the left and right children to compare with the father

• If you are younger than your father, exchange with your father
• If you are older than your father, stop the exchange. At this time, it has formed a heap

3. The worst-case swap stops when the child is a leaf node

Code implementation:

//exchange
void swap(int* px, int *py)
{
	int tmp = 0;
	tmp = *px;
	*px = *py;
	*py = tmp;
}

//Adjust the algorithm downward. Condition: the left and right subtrees are heaps

//Let's assume that it is built as a small heap (modify it accordingly for a large pile)

//a is the first address of the array, n is the number of data, and parent is the parent node
void AdjustDown(int* a, int n, int parent)
{
	int child = parent * 2 + 1;//Default to left child first
	
    //The end condition is that the subscript of child is less than n. when child is a leaf node, the next child is greater than n, and the cycle ends
	while (child < n)
	{
		//Find the small child and make the child the smaller one
		if ((child + 1 < n) && (a[child + 1] < a[child]))
		{
			child++;//The right child has more subscripts by default than the left child
		}

		//1. If the younger child is younger than the father, exchange and continue to adjust downward
		//2. If the younger child is older than the father, end the adjustment

		if (a[child] < a[parent])
		{
			//exchange
			swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

The downward adjustment algorithm has been finished, but we will find that it is very weak. It can only form a heap under specific circumstances. So how to ensure that a heap can be formed under normal circumstances?

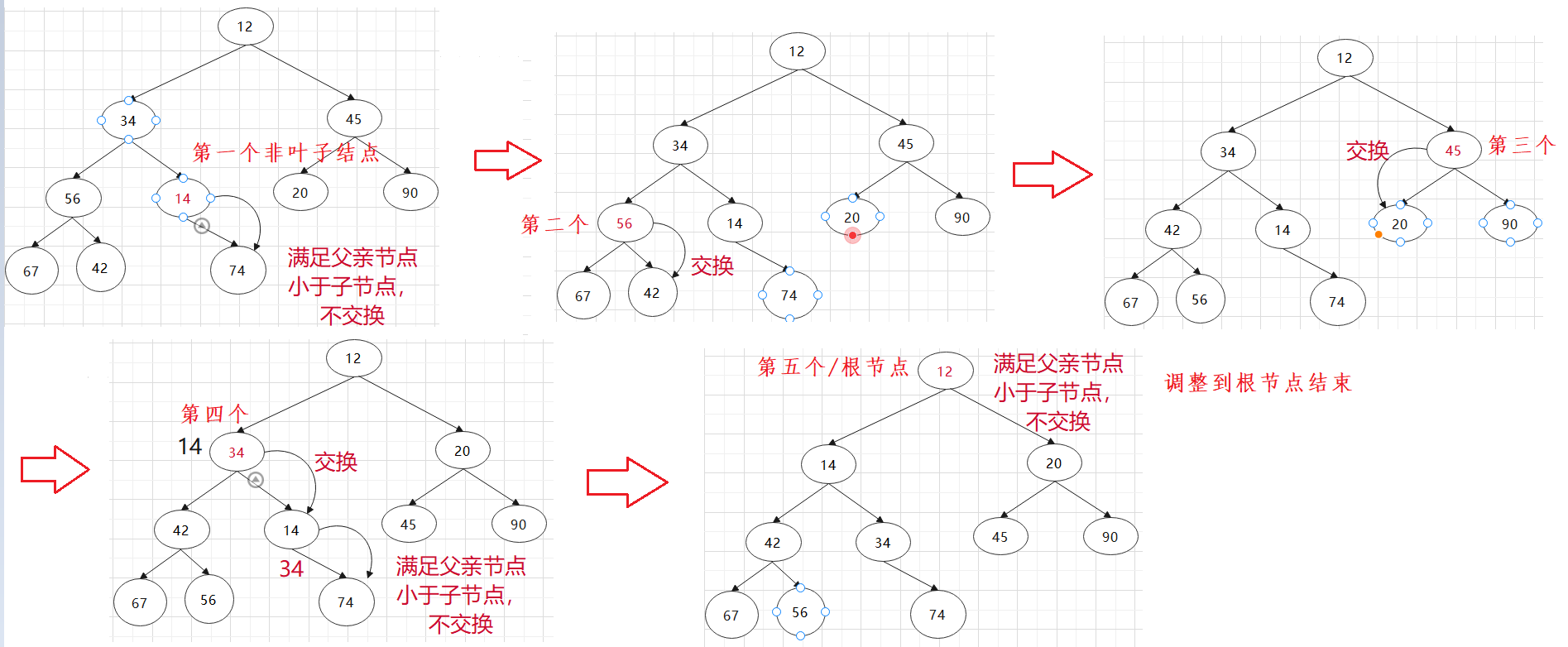
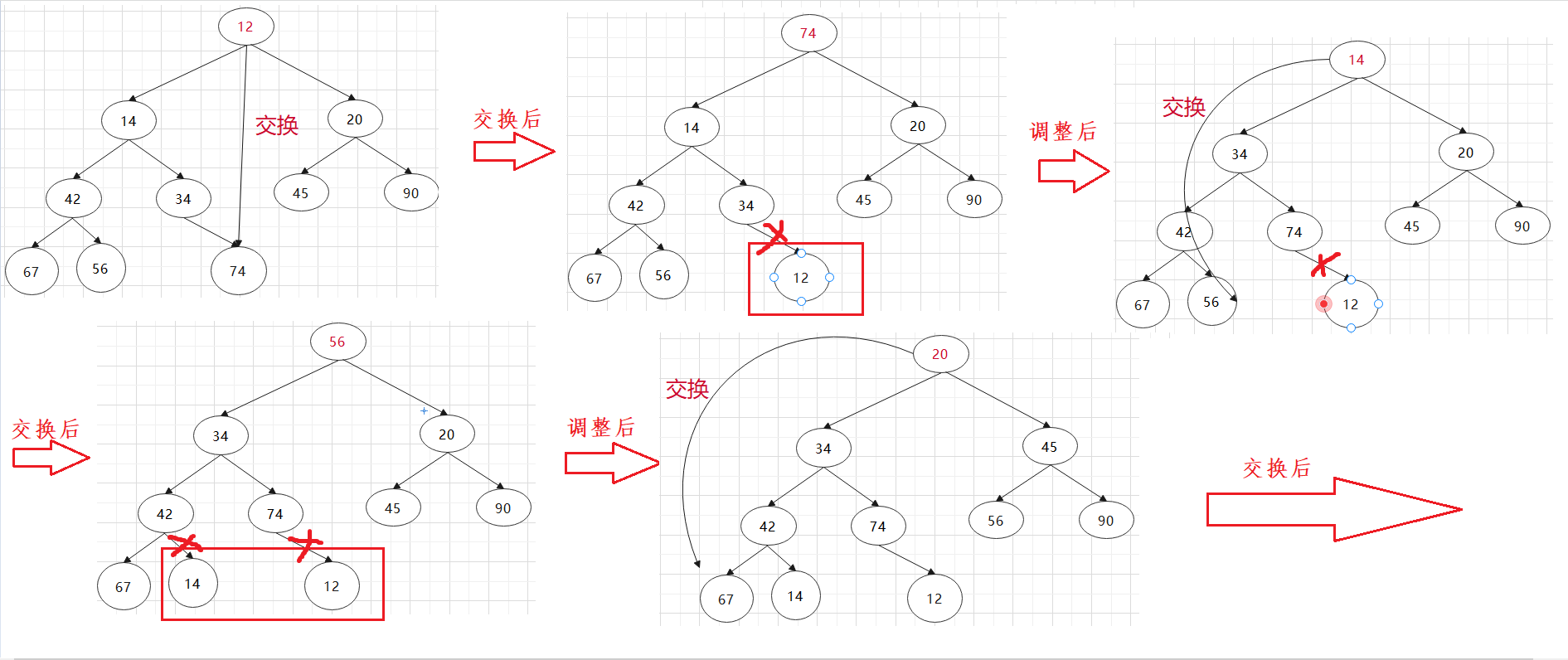
First, give a complete binary tree that does not satisfy that the left and right subtrees are stacked, int arr[] = {12, 34, 45, 56, 14, 20, 90, 67, 42, 74};
We make this complete binary tree into a small pile.

Main ideas:

1. Adjust downward from the penultimate non leaf node
2. Stop when adjusting to the root node

Code implementation:

//Build a small pile
//The initial value of i is the subscript of the first non leaf node
for (int i = (n - 1 - 1) / 2; i >= 0; i--)
{
	//Adjust downward from the penultimate non leaf node to the root node
	AdjustDown(a, n, i);
}
//After adjustment, you get a small root heap

After adjusting the algorithm downward, the general complete binary tree has formed a heap. How to sort now?

Implementation of sorting

In order to realize sorting, we should consider whether to sort in ascending order or descending order. There is a distinction between building a large pile and building a small pile. So how can we choose the best?

Ascending order: it is better to build a large pile, but it is also OK to build a small pile, which can not reflect the value brought by building a pile
Descending order: it's better to build a small pile. The same is true

So how to sort?

1. The heap has been built. The first value is the minimum (if it is a heap, the first value is the maximum). Exchange the first value with the last value and store it
2. Remove the last number, adjust it downward from the root node, repeat the operation, get the minimum value in turn, and store it until only the last number is left.

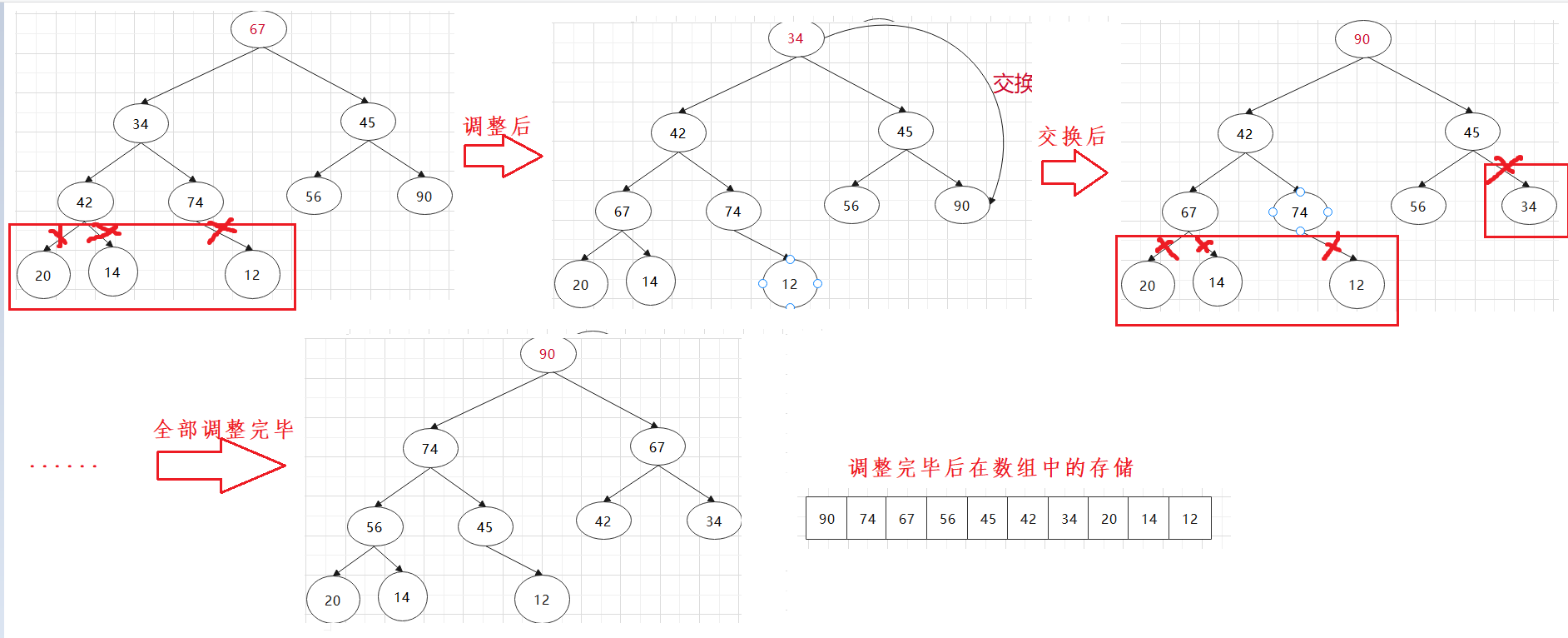
Code implementation:

int end = n - 1;
	while (end > 0)
	{
		swap(&a[0], &a[end]);//The minimum value is exchanged with the subsequent elements of the array and stored behind the array to form a descending order
		AdjustDown(a, end, 0);//Then adjust it in turn to get the minimum value
		end--;
	}

Heap sort complete code

Dynamic diagram:

code:

#include<stdio.h>

//exchange
void swap(int* px, int *py)
{
	int tmp = 0;
	tmp = *px;
	*px = *py;
	*py = tmp;
}

//Adjust the algorithm downward. Condition: the left and right subtrees are heaps

//Let's assume that it is a small heap (modify it accordingly if there is a large heap)
void AdjustDown(int* a, int n, int parent)
{
	int child = parent * 2 + 1;//Default to left child

	while (child < n)
	{
		//Find the little one around
		if ((child + 1 < n) && (a[child + 1] < a[child]))
		{
			child++;//The right child has more subscripts by default than the left child
		}

		//1. If the younger child is younger than the father, exchange and continue to adjust downward
		//2. If the younger child is older than the father, end the adjustment

		if (a[child] < a[parent])
		{
			//exchange
			swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

void HeapSort(int* a, int n)
{
	//Build a small pile
	for (int i = (n - 1 - 1) / 2; i >= 0; i--)
	{
		//Adjust downward from the penultimate non leaf node to the root node
		AdjustDown(a, n, i);
	}
	//After adjustment, you get a small root heap

	//Descending order
	int end = n - 1;
	while (end > 0)
	{
		swap(&a[0], &a[end]);//The minimum value is exchanged with the subsequent elements of the array and stored behind the array to form a descending order

		AdjustDown(a, end, 0);//Then adjust it in turn to get the minimum value

		end--;
	}
}

int main()
{
	int a[] = { 12, 34, 45, 56, 14, 20, 90, 67, 42, 74 };

	//Heap sort 
	HeapSort(a, sizeof(a) / sizeof(int));

	//print data
	for (int i = 0; i < sizeof(a) / sizeof(int); i++)
	{
		printf("%d ", a[i]);
	}
	return 0;
}

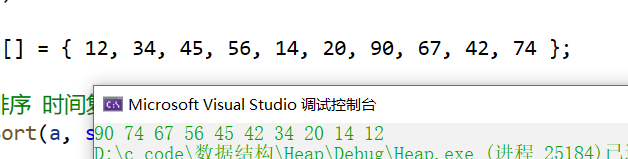
success!!!

Time complexity analysis of reactor construction

Therefore, the time complexity of heap sorting is O(N*log2N)(2 is the base)