1. Priority queue
1.1 concept
Queue is a first in first out data structure, but in some cases, the data operated may have priority. Generally, when leaving the queue, elements with high priority may be required to leave the queue. In this scenario, it is obviously inappropriate to use the queue. For example, when playing games on the mobile phone, if a call comes in, the system should process the queue first.
In this case, our data structure should provide two basic operations, one is to return the highest priority object, and the other is to add a new object. This data structure is called priority queue.
1.2 introduction to common interfaces
1.2.1 characteristics of PriorityQueue
Note about the use of PriorityQueue:
- When using, you must import the package where PriorityQueue is located, that is:
import java.util.PriorityQueue;
- The elements placed in the PriorityQueue must be able to compare the size, and cannot insert objects that cannot compare the size, otherwise classcastexpectation exception will be thrown.
- Cannot insert null object, otherwise NullPointerExpection will be thrown.
- There is no capacity limit. You can insert any number of elements, and its internal capacity can be expanded automatically.
- The time complexity of inserting and deleting elements is O ( l o g 2 N ) O(log_2N) O(log2N).
- The underlying PriorityQueue uses a heap data structure (described later).
- PriorityQueue is a small heap by default - that is, the smallest element is obtained every time.
1.2.2 introduction to common interfaces of PriorityQueue
- Construction of priority queue
Only several construction methods are listed here. For other methods, please refer to the help document.
| constructor | Function introduction |
|---|---|
| PriorityQueue() | Create an empty priority queue |
| PriorityQueue(int initialCapacity) | Create a priority queue with an initial capacity of initialCapacity. Note: initialCapacity cannot be less than 1, or an ILLegalArgumentException will be thrown |
| PriorityQueue(Collection<?extends E>c) | Use a collection to create priority queues |
public class Priority {
static void TestPriorityQueue(){
//Create an empty priority queue
PriorityQueue<Integer> p1=new PriorityQueue<>();//The default capacity is 11
//Create an empty priority queue with the underlying capacity of initialCapacity
PriorityQueue<Integer> p2=new PriorityQueue<>(100);
ArrayList<Integer> list=new ArrayList<>();
list.add(4);
list.add(3);
list.add(2);
list.add(1);
PriorityQueue<Integer> p3=new PriorityQueue<>(list);
System.out.println(p3.size());
System.out.println(p3.peek());
}
public static void main(String[] args) {
TestPriorityQueue();
}
}
Note: by default, the PriorityQueue queue is a small heap. If a large heap is required, the user needs to provide a comparator.
- User provided comparator
public class Card {
String rank;
String suit;
public Card(String rank,String suit){
this.rank=rank;
this.suit=suit;
}
}
public class CardCmp implements Comparator<Card>{
@Override
public int compare(Card o1, Card o2) {
o1.rank.compareTo(o2.rank) ;
return 0;
}
}
Verification: the elements placed in the PriorityQueue must be able to compare sizes, otherwise classcastexpectation will be thrown
public static void method3(){
PriorityQueue<Card> p=new PriorityQueue<>(new CardCmp());
p.offer(new Card("A","♠"));
p.offer(new Card("K","♠"));
}
- By default, it is a small heap. How to create a large heap---- The starting element is the largest
public static void method4(){
PriorityQueue<Integer> p=new PriorityQueue<>(new Comparator<Integer>() {
@Override
public int compare(Integer o1, Integer o2) {
return o2-o1;//o2-o1 is a large pile and o1-o2 is a small pile
}
});
p.offer(5);
p.offer(1);
p.offer(4);
p.offer(2);
p.offer(3);
}
Insert / delete / get the highest priority element
| Function name | Function introduction |
|---|---|
| boolean offer(E e) | Insert element E and return true after successful insertion. If the e object is empty, a NullPointerException exception will be thrown, which reduces the time complexity O ( l o g 2 N ) O(log_2N) O(log2 # N), note: capacity expansion will be carried out when the space is insufficient |
| E peek() | Gets the element with the highest priority. If the priority queue is empty, null is returned |
| E poll() | Remove the element with the highest priority and return it. If the priority queue is empty, return null |
| int size() | Get the number of valid elements |
| void clear() | empty |
| boolean isEmpty() | Check whether the priority queue is empty. If it is empty, return true |
public static void method2(){
PriorityQueue<Integer> p=new PriorityQueue<>();
p.offer(5);
p.offer(1);
p.offer(4);
p.offer(2);
p.offer(3);
System.out.println(p.size());
p.offer(null);//Null pointer exception
System.out.println(p.peek());//Get the top of heap element -- that is, the element with the highest or lowest priority
p.poll();
p.poll();
p.poll();
System.out.println(p.peek());
p.clear();
if(p.isEmpty()){
System.out.println("p is empty");
}else{
System.out.println("p is not empty");
}
}
The following is the capacity expansion method of PriorityQueue:
public class Test {
private static final int MAX_ARRAY_SIZE=Integer.MAX_VALUE-8;
private void grow(int minCapacity){
int oldCapacity= queue.length;
int newCapacity=oldCapacity+((oldCapacity<64)?(oldCapacity+2):(oldCapacity>>1));
if(newCapacity-MAX_ARRAY_SIZE>0){
newCapacity=hugeCapacity(minCapacity);
queue= Arrays.copyOf(queue,newCapacity);
}
}
private static int hugeCapacity(int minCapacity){
if(minCapacity<0){
throw new OutOfMemoryError();
return (minCapacity>MAX_ARRAY_SIZE)?Integer.MAX_VALUE:MAX_ARRAY_SIZE;
}
}
}
Description of priority queue expansion:
- If the capacity is less than 64, it is expanded by twice the oldCapacity.
- If the capacity is greater than 64, it is expanded by 1.5 times the oldCapacity.
- If the capacity exceeds MAX_ARRAY_SIZE, according to MAX_ARRAY_SIZE for capacity expansion.
1.3 application of priority queue
top-k: the largest or smallest top k data.
top-k problem: the minimum number of K
class Solution {
public int[] smallestK(int[] arr, int k) {
if(arr==null){
return new int[0];
}
//Construct a small heap with all the elements in the array
PriorityQueue<Integer> p=new PriorityQueue<>();
for(int i=0;i<arr.length;++i){
p.offer(arr[i]);
}
//Get the first k elements in the heap
int[] ret =new int[k];
for(int i=0;i<k;++i){
ret[i]=p.poll();
}
return ret;
}
}
2. Simulation implementation of priority queue
The underlying PriorityQueue uses the data structure of the heap, and the heap actually adjusts some elements based on the complete binary tree.
2.1 concept of reactor
If there is a key set K={
k
0
,
k
1
,
k
−
2
,
.
.
.
,
k
n
−
1
k_0,k_1,k-2,...,k_n-1
k0, k1, K − 2,..., kn − 1}, store all its elements in the order of a complete binary tree. In a one-dimensional array, if ki < = k2i + 2 (KI > = k2i + 2) I = 0,1,2... Is satisfied, it is called small heap (or large heap). The heap with the largest root node is called the maximum heap or large root heap, and the heap with the smallest root node is called the minimum heap or small root heap.
Nature of heap:
- The value of a node in the heap is always not greater than or less than the value of its parent node;
- There is always a complete binary tree in the heap;
2.2 storage mode of heap
According to the concept of heap, heap is a complete binary tree, so it can be stored in sequence according to the rules of sequence.
Note: sequential storage is not suitable for incomplete binary trees.
Reason: in order to restore the binary tree, empty nodes must be stored in the space, which will lead to low space utilization.
After the elements are stored in the array, the tree can be restored according to the nature 5 of the binary tree part. Assuming i is the subscript of the node in the array, there are:
- If I is 0, the node represented by I is the root node, otherwise the parent node of I node is (i-1)/2
- If 2i+1 is less than the number of nodes, the left child subscript of node i is 2i+1, otherwise there is no left child
- If 2i+2 is less than the number of nodes, the subscript of the right child of node i is 2i+2, otherwise there is no right child
2.3 creation of heap
2.3.1 reactor downward adjustment
How to create a heap of data in the set {27,15,19,18,28,34,65,49,25,37}?
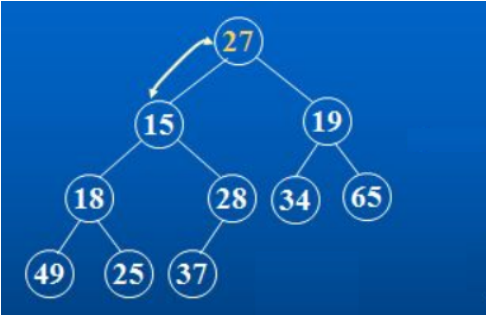
It is found from the above figure that the left and right subtrees of the root node have fully satisfied the nature of the heap, so you only need to adjust the root node downward.
Downward adjustment process:
- Let the parent mark the node to be adjusted, and the child mark the left child of the parent.
- If the left child of the parent exists, that is, child < size, perform the following operations to know that the left child of the parent does not exist
- parent whether the right child exists. Find the smallest child among the left and right children and let the child mark
- Compare the parent with the child. If the parent is larger than the child, exchange the two. If the large element in the parent moves downward, the subtree may not meet the properties, so it needs to continue to adjust downward
// Function: adjust the binary tree with parent as the root
// Premise: it must be ensured that the left and right subtrees of the parent have met the characteristics of the heap
// Time complexity: O(logN)
private void shiftDown(int parent){
// By default, let the child mark the left child first - because: the parent may have left or not right
int child = parent*2 + 1;
// The while loop condition can ensure that the left child of the parent must exist
// However, there is no guarantee that the right child of the parent exists
while(child < size){
// 1. Find the younger of the left and right children
if(child+1 < size && array[child+1] < array[child]){
child += 1;
}
// 2. The younger child has been found
// Test whether parents and children meet the characteristics of heap
if(array[parent] > array[child]){
swap(parent, child);
// If large parents go down, the subtree may not meet the characteristics of heap
// Therefore, it needs to continue to adjust downward
parent = child;
child = parent*2 + 1;
}else{
// A binary tree with a parent as the root is already a heap
return;
}
}
}
Note: when adjusting the binary tree with parent as the root, the left and right subtrees of the parent must be heap before downward adjustment.
Time complexity: from the root node to the leaf node, the number of comparisons is the height of the complete binary tree, i.e
O
(
l
o
g
2
N
)
O(log_2N)
O(log2N)
2.3.2 creation of heap
So how to adjust the ordinary sequence {1,5,3,8,7,6}, that is, the left and right subtrees of the root node do not meet the characteristics of the heap?
public MyPriorityQueue(Integer[] arr){
// 1. Copy the elements in arr to the array
array = new Integer[arr.length];
for(int i = 0; i < arr.length; ++i){
array[i] = arr[i];
}
size = arr.length;
// 2. Find the penultimate leaf node in the current complete binary tree
// Note: the penultimate leaf node is just the parent of the last node
// The number of the last node is size-1, and the index of the penultimate non leaf node is (size-1-1)/2
int lastLeafParent = (size-2)/2;
// 3. From the position of the penultimate leaf node to the position of the root node, use downward adjustment
for(int root = lastLeafParent; root >= 0; root--){
shiftDown(root);
}
}
2.3.3 time complexity of reactor construction
Because the heap is a complete binary tree, and the full binary tree is also a complete binary tree, the full binary tree is used here for simplification.
Suppose the height of the tree is h:

Note: leaf nodes do not need to be adjusted because they are adjusted from the penultimate non leaf node.
Level 1,
2
0
2^0
20 nodes, need to move down the h-1 layer;
Level 2,
2
1
2^1
21 nodes, need to move down the h-2 layer;
Level 3,
2
2
2^2
22 nodes, need to move down the h-3 layer;
Level 4,
2
3
2^3
23 nodes, need to move down the h-4 layer;
...
Layer h-1,
2
h
−
2
2^{h-2}
2h − 2 nodes, need to move down 1 layer;
The total number of steps to move the node:
T
(
n
)
=
2
0
∗
(
h
−
1
)
+
2
1
∗
(
h
−
2
)
+
2
2
∗
(
h
−
3
)
+
2
3
∗
(
h
−
4
)
+
.
.
.
+
2
h
−
3
∗
(
2
)
+
2
h
−
2
∗
(
1
)
T(n)=2^0*(h-1)+2^1*(h-2)+2^2*(h-3)+2^3*(h-4)+...+2^{h-3}*(2)+2^{h-2}*(1)
T(n)=20∗(h−1)+21∗(h−2)+22∗(h−3)+23∗(h−4)+...+2h−3∗(2)+2h−2∗(1) ------------ ①
2
T
(
n
)
=
2
1
∗
(
h
−
1
)
+
2
2
∗
(
h
−
2
)
+
2
3
∗
(
h
−
3
)
+
2
4
∗
(
h
−
4
)
+
.
.
.
+
2
h
−
2
∗
(
2
)
+
2
h
−
1
∗
(
1
)
2T(n)=2^1*(h-1)+2^2*(h-2)+2^3*(h-3)+2^4*(h-4)+...+2^{h-2}*(2)+2^{h-1}*(1)
2T(n)=21∗(h−1)+22∗(h−2)+23∗(h−3)+24∗(h−4)+...+2h−2∗(2)+2h−1∗(1) -------------②
② - ① offset subtraction:
T
(
n
)
=
1
−
h
+
2
1
+
2
2
+
2
3
+
2
4
+
.
.
.
+
2
h
−
2
+
2
h
−
1
T(n)=1-h+2^1+2^2+2^3+2^4+...+2^{h-2}+2^{h-1}
T(n)=1−h+21+22+23+24+...+2h−2+2h−1
=
2
0
+
2
1
+
2
2
+
2
3
+
2
4
+
.
.
.
+
2
h
−
2
+
2
h
−
1
−
h
=2^0+2^1+2^2+2^3+2^4+...+2^{h-2}+2^{h-1}-h
=20+21+22+23+24+...+2h−2+2h−1−h
=
2
h
−
1
−
h
=2^h-1-h
=2h−1−h
And because n=
2
h
−
1
2^h-1
2h−1,
h
=
l
o
g
2
(
n
+
1
)
h=log_2(n+1)
h=log2(n+1)
T
(
n
)
=
n
−
l
o
g
2
(
n
+
1
)
≈
n
T(n)=n-log_2(n+1)≈n
T(n)=n−log2(n+1)≈n
2.4 heap insertion and deletion
2.4.1 insertion of reactor
The insertion of the heap requires a total of two steps:
- First put the elements into the underlying space (Note: when the space is insufficient, it needs to be expanded)
- Adjust the last newly inserted node upward until it meets the nature of the heap
private void shiftUp(int child){
//Find child's parents
int parent = (child-1)/2;
while(child != 0){
if(array[child] < array[parent]){
swap(child, parent);
child = parent;
parent = (child-1)/2;
}else{
return;
}
}
}
2.4.2 deletion of heap
Note: the deletion of the heap must be the top element of the heap.
- Swap the top element with the last element
- Reduce the number of valid elements in the heap by one
- Adjust the heap top element downward
2.5 implementation of priority queue with heap simulation
public class MyPriorityQueue {
Integer[] array;
int size; // Number of valid elements
boolean offer(Integer e){
if(e == null){
throw new NullPointerException("When inserting, the element is null");
}
ensureCapacity();
array[size++] = e;
// Note: when a new element is inserted, it may destroy the nature of the heap - it needs to be adjusted upward
shiftUp(size-1);
return true;
}
// Delete the elements at the top of the heap
public Integer poll(){
if(isEmpty()){
return null;
}
Integer ret = array[0];
// 1. Exchange the top element of the heap with the last element in the heap
swap(0, size-1);
// 2. Reduce the number of effective elements in the heap by one
size--; // size -= 1;
// 3. Adjust the top element down to the proper position
shiftDown(0);
return ret;
}
public int size(){
return size;
}
public boolean isEmpty(){
return size == 0;
}
public void clear(){
size = 0;
}
public int peek(){
return array[0];
}
}
3. Application of reactor
3.1 implementation of PriorityQueue
Encapsulating priority queues with heap as the underlying structure
3.2 heap sorting
Heap sorting is sorting with the idea of heap, which is divided into two steps:
- Build pile
Ascending order: build a pile
Descending order: build small piles - Use the idea of heap deletion to sort
public static void swap(int [] array,int left,int right){
int temp=array[right];
array[right]=array[left];
array[left]=array[right];
}
public static void shiftDown(int[] array,int size, int parent){
int child =parent*2+1;
while(child<size){
//Find the older of the left and right children
if(child+1<size&&array[child+1]>array[child]){
child+=1;
}
//Parents are smaller than older children
if(array[parent]<array[child]){
swap(array,parent,child);
}
}
}
//Hypothesis: ascending order
public static void heapSort(int[] array){
//1. Build pile --- build a large pile in ascending order and a small pile in descending order
for(int root=(array.length-2)>>1;root>=0;root--){
shiftDown(array,array.length,root);
}
//2. Use the idea of heap deletion to sort - adjust down
int end=array.length-1;//Mark the last element with end
while(end!=0){
swap(array,0,end);
shiftDown(array,end,0);
end--;
}
}
3.3 Top-k problem
Top-k problem: find the first K largest or smallest elements in the data set. Generally, the amount of data is relatively large.
For the top-k problem, the easiest way to think of is sorting, but if the amount of data is very large, sorting is not very desirable. The best way is to solve it with heap. The basic idea is as follows:
- Use the first K elements in the data set to build the heap
The first K largest elements build a small heap
The first K smallest elements are built in a pile - Compare the remaining N-K elements with the heap top elements in turn. If not, replace the heap top elements
After comparing the remaining N-K elements with the top elements in turn, the remaining K elements in the heap are the first K minimum or maximum elements.