Experimental purpose
Understand the data structure and allocation algorithm used in dynamic partition allocation, and further deepen the understanding of dynamic partition storage management and its implementation process.
Experimental content
(1) The dynamic partition allocation process alloc() and the recovery process free() using the first adaptation algorithm and the best adaptation algorithm are implemented in C language. Among them, the free partition is managed through the free partition chain: when allocating memory, the system gives priority to the low-end space of the free partition.
(2) It is assumed that in the initial state, the available memory space is 640KB, and there are the following request sequences:
- Job 1 request 130KB.
- Job 2 request 60KB.
- Job 3 request 100KB.
- Job 2 releases 60KB.
- Job 4 request 200KB.
- Job 3 releases 100KB.
- Job 1 frees 130KB.
- Job 5 request 140KB.
- Job 6 request 60KB.
- Job 7 request 50KB.
- Job 6 releases 60KB.
Please use the first adaptation algorithm and the best adaptation algorithm to allocate and recycle memory blocks respectively. It is required to display the idle partition chain after each allocation and recycling.
code
Linked list implementation [sending]
I haven't worked out the experimental class all afternoon today. I didn't finish it until 7 p.m.
I wrote it by myself. I encountered several problems:
- Dynamically allocate storage
(this must be remembered. Because I didn't have dynamic allocation, I was confused at the beginning and didn't output any results)
workspace *L=new workspace; - Both algorithms traverse the linked list from beginning to end. First fit only needs to find the first empty interval, and best fit needs to find the space with the smallest difference min_minu from the target space
(I didn't understand this at the beginning, so I always added nodes at the end of the linked list) - At the beginning, there is a maximum empty section with memory of 640KB. During initialization, a t can be inserted after the header node_ T is used as this empty interval, and the head node can also be used as the maximum empty interval. I use the first. [indeed, my head node here is basically useless. It's good-looking. Users can modify it slightly]
- The code of the best adaptation method is similar to that of the first adaptation method, but the difference is that alloc dynamically applies for allocation. The best adaptation method finds the first suitable empty interval on the basis of the first adaptation, breaks the loop, traverses backward from the interval, and finds a possible interval smaller than the current empty interval. If it does not exist, the current interval is used. Pay attention to some small problems in timely break and pointer pointing.
- Problems with pointers.
Through workspace *s=t, you cannot modify the value in memory, only the address pointed to by the pointer. Here, the previous node is marked, and the next of the previous node points to a newly allocated space for memory modification. - Possible conflicts between the two algorithms.
This experiment can divide the two algorithms into two files for acceptance. It is not mandatory to write two files in the same file. A single file needs to point the header node to a NULL pointer during algorithm initialization to prevent conflicts.
#include<bits/stdc++.h>
using namespace std;
struct workspace
{
int id;
int begin;
int end;
int size;
workspace *next;
};
workspace *L=new workspace;
int work[11][3]={
{1,130,1},
{2,60,1},
{3,100,1},
{2,60,0},
{4,200,1},
{3,100,0},
{1,130,0},
{5,140,1},
{6,60,1},
{7,50,1},
{6,60,0}
};
void show()
{
cout<<"============"<<endl;
workspace *s=L;
s=L->next;
while(s->next)
{
cout<<s->id<<"->";
s=s->next;
}
cout<<s->id<<endl;
}
void firstfit()
{
workspace *s=L;
L->begin=0;
L->end=0;
L->size=0;
L->next=NULL;
workspace *t_t=new workspace;
t_t->id=0;
t_t->begin=0;
t_t->end=640;
t_t->size=640;
t_t->next=NULL;
L->next=t_t;
for(int i=0;i<11;i++)
{
if(work[i][2]==1)
{
workspace *t=new workspace;
t->id=work[i][0];
t->size=work[i][1];
s=L;
workspace *tt=s;
while(s)
{
if((s->size>=work[i][1])&&(s->id==0))
{
t->begin=s->begin;
t->end=t->begin+work[i][1];
if(s->size>work[i][1])
{
workspace *temp=new workspace;
temp->next=s->next;
temp->id=0;
temp->begin=t->end+1;
temp->end=s->end;
temp->size=s->size-work[i][1];
t->next=temp;
}
else if(s->size==work[i][1])
{
t->next=s->next;
}
tt->next=t;
break;
}
tt=s;
s=s->next;
}
}
else if(work[i][2]==0)
{
s=L;
while(s->next)
{
if(s->id==work[i][0])
{
s->id=0;
break;
}
s=s->next;
}
workspace *t;
s=L;
t=s;
while(s->next)
{
if(s->id==0)
{
if(t->id==0)
{
t->end=s->next->end;
t->size=t->size+s->next->size;
t=s->next;
}
if(s->next->id==0)
{
s->end=s->next->end;
s->size=s->size+s->next->size;
s->next=s->next->next;
}
break;
}
t=s;
s=s->next;
}
}
show();
}
cout<<endl;
cout<<"Current dynamic partitioned storage:"<<endl;
s=L->next;
while(s->next)
{
cout<<s->id<<"->";
s=s->next;
}
cout<<s->id<<endl;
}
void bestfit()
{
workspace *s=L;
L->begin=0;
L->end=0;
L->size=0;
L->next=NULL;
workspace *t_t=new workspace;
t_t->id=0;
t_t->begin=0;
t_t->end=640;
t_t->size=640;
t_t->next=NULL;
L->next=t_t;
for(int i=0;i<11;i++)
{
if(work[i][2]==1)
{
workspace *t=new workspace;
t->id=work[i][0];
t->size=work[i][1];
s=L;
workspace *tt=s;
while(s)
{
if((s->size>=work[i][1])&&(s->id==0))
{
break;//Find the first suitable node and jump out of the loop
}
tt=s;
s=s->next;
}
workspace *ttt=s;
workspace *j=s->next;
int min_minu=ttt->size-work[i][1];//Record the difference between the currently suitable node and the target partition
workspace *min_pre=s;//Record previous node
workspace *min_num=s;//Record the current minimum node
for(;j!=NULL;j=j->next)
{
if((j->size>=work[i][1])&&(j->id==0))
{
if(j->size-work[i][1]<min_minu)
{
min_pre=ttt;//Record previous node
min_num=j;
}
}
ttt=j;
}
if(s==min_num)
{
min_pre=tt;
}
t->begin=min_num->begin;
t->end=t->begin+work[i][1];
if(min_num->size>work[i][1])
{
workspace *temp=new workspace;
temp->next=min_num->next;
temp->id=0;
temp->begin=t->end+1;
temp->end=min_num->end;
temp->size=min_num->size-work[i][1];
t->next=temp;
}
else if(min_num->size==work[i][1])
{
t->next=min_num->next;
}
min_pre->next=t;
}
else if(work[i][2]==0)
{
s=L;
while(s->next)
{
if(s->id==work[i][0])
{
s->id=0;
break;
}
s=s->next;
}
workspace *t;
s=L;
t=s;
while(s->next)
{
if(s->id==0)
{
if(t->id==0)
{
t->end=s->next->end;
t->size=t->size+s->next->size;
t=s->next;
}
if(s->next->id==0)
{
s->end=s->next->end;
s->size=s->size+s->next->size;
s->next=s->next->next;
}
break;
}
t=s;
s=s->next;
}
}
show();
}
cout<<endl;
cout<<"Current dynamic partitioned storage:"<<endl;
s=L->next;
while(s->next)
{
cout<<s->id<<"->";
s=s->next;
}
cout<<s->id<<endl;
}
int main()
{
L->next=NULL;
cout<<"First adaptation algorithm:"<<endl;
firstfit();
cout<<endl;
cout<<endl;
L->next=NULL;
cout<<"Optimal adaptation algorithm:"<<endl;
bestfit();
return 0;
}
Operation results
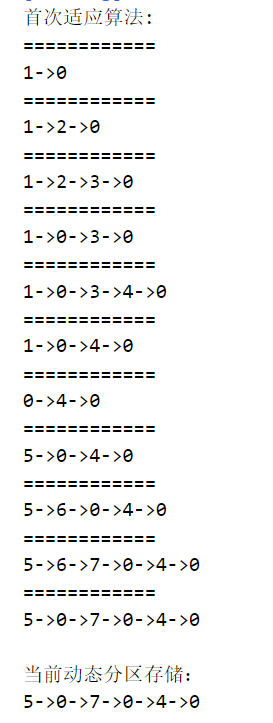

reflection
(1) What are the different effects of the first adaptation algorithm and the best adaptation algorithm on the speed of memory allocation and recovery?
The free partitions of the first adaptation algorithm are arranged in the order of increasing addresses. Each time memory is allocated, look up the free table (or free partition chain) in order to find the first free partition whose size can meet the requirements and allocate it to the process. Overall, the performance is the best and the algorithm overhead is small. Generally, there is no need to reorder the idle partition queue after recycling the partition. In order to ensure that there is a large continuous space when the "big process" arrives, the best adaptation algorithm can leave as many free areas as possible, that is, give priority to using smaller free areas. More large partitions will be retained to better meet the needs of large processes, resulting in many too small and difficult to use fragments and high algorithm overhead. After recovering partitions, it may be necessary to reorder the queue of idle partitions.
(2) How to solve the problem of memory allocation speed reduction caused by fragmentation?
Discrete allocation of memory, the introduction of discontinuous allocation, allows a program to load non adjacent memory partitions dispersedly, and requires additional space to store the indexes of scattered areas.