Experiment 4 design and implementation of neural network algorithm for handwritten digit recognition

1, Experimental purpose

By learning BP neural network technology, handwritten digits are recognized, and the recognition rate is improved by structure based recognition method and template matching method.

2, Experimental equipment

PC matlab software

3, Experimental content

According to the BP neural network design method, the two-layer BP network is selected to construct the training sample set, and form the input vector and target vector required for training. The digital original image is obtained through the drawing tool, the maximum rectangular area with image pixel 0 is intercepted, which is transformed into a 16 * 16 binary image after set transformation, and then inverse color processing is carried out, The image data feature is extracted as the input vector of neural network. Experiments show that the application of BP neural network in handwritten digit recognition has high recognition rate and reliability.

4, Experimental principle

BP algorithm consists of two processes: forward calculation of data flow (forward propagation) and back propagation of error signal. During forward propagation, the propagation direction is input layer → hidden layer → output layer, and the state of neurons in each layer only affects the neurons in the next layer. If the desired output is not obtained in the output layer, it turns to the back propagation process of error signal. Through the alternation of these two processes, The gradient descent strategy of error function is implemented in the weight vector space, and a group of weight vectors are searched dynamically and iteratively to minimize the network error function, so as to complete the process of information extraction and memory

5, Experimental steps

1. Firstly, the handwritten digital image is preprocessed, including binarization, denoising, tilt correction, normalization and feature extraction, and the input vector m and target vector target of BP neural network are generated, in which m is selected as 40 × The first to tenth columns of the matrix of 10 represent numbers from 0 to 9. The target is 9 × 10 unit matrix, each number outputs 1 at its sequential position and 0 at other positions
2. Then the training process of neural network is the basis of character recognition, which is directly related to the recognition rate. The training samples are sent to BP neural network for training, and the weight is repeatedly adjusted in the gradient direction to minimize the square sum error of the network. The learning method adopts the steepest descent method. The number of input nodes is 16 * 16 = 256, the hidden layer transfer function is sigmoid function (logsig), an output node, the output transfer function is pureline(purelin), and the number of hidden layer nodes is sqrt(256+1)+a(a=1~10), which is taken as 25. After training, the number to be identified is sent to BP neural network for simulation test.
Analyze operation results

6, Specific process of experiment

Construct training sample set. It also constitutes training input samples and target vectors. Through the drawing tool, the images of numbers 0 ~ 9 are obtained: (0, 10, 20, 30, 40, 50, 60, 70, 80, 90). Different writing methods of 0 stored in bmp, (1, 11, 21, 31, 41, 51, 61, 71, 81, 91). Different writing methods of 1 stored in bmp,... And so on, 100 images are obtained.

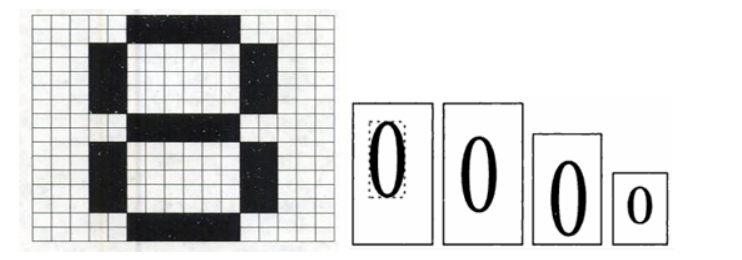
7, Experimental code

clear all;
'Generating input vector and target vector, please wait...'
for kk=0:99
    p1=ones(16,16);
    m=strcat(int2str(kk),'.bmp');
    x=imread(m,'bmp');
    bw=im2bw(x,0.5);
    [i,j]=find(bw==0);
    imin=min(i);
    imax=max(i);
    jmin=min(j);
    jmax=max(j);
    bwl=bw(imin:imax,jmin:jmax);
    rate=16/max(size(bwl));
    bwl=imresize(bwl,rate); [i,j]=size(bwl);
i1=round((16-i)/2);
 j1=round((16-j)/2);
 p1(i1+1:i1+i,j1+1:j1+j)=bwl;
 p1=-1.*p1+ones(16,16);
 %The input vector of neural network is formed from image data
 for m=0:15
p(m*16+1:(m+1)*16,kk+1)=p1(1:16,m+1);
 end
 %Form neural network target vector
 switch kk
   case{0,10,20,30,40,50,60,70,80,90}
             t(kk+1)=0;
   case{1,11,21,31,41,51,61,71,81,91}
             t(kk+1)=1;
   case{2,12,22,32,42,52,62,72,82,92}
             t(kk+1)=2;
   case{3,13,23,33,43,53,63,73,83,93}
             t(kk+1)=3;
   case{4,14,24,34,44,54,64,74,84,94}
 u            t(kk+1)=4;
   case{5,15,25,35,45,55,65,75,85,95}
             t(kk+1)=5;
   case{6,16,26,36,46,56,66,76,86,96}
             t(kk+1)=6;
   case{7,17,27,37,47,57,67,77,87,97}
             t(kk+1)=7;
   case{8,18,28,38,48,58,68,78,88,98}
             t(kk+1)=8;
   case{9,19,29,39,49,59,69,79,89,99}
             t(kk+1)=9;
  end
end
save E52PT p t;
'End of generation of input vector and target vector!'

Experimental results:

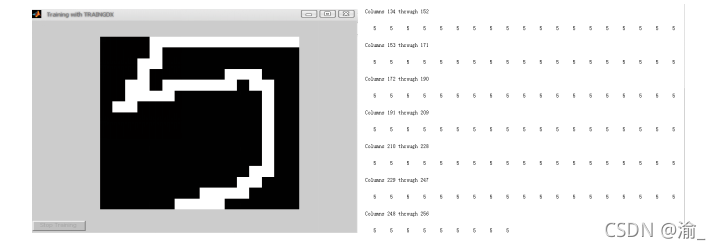
1. Image preprocessing: intercept the largest rectangular area of the digital image with prime value of 0 (black), and transform the image of this area into a 16 * 16 binary image. Then, the binary image is inversely processed to obtain the values 0 and 1 of the pixels of the image, which constitute the input vector of the neural network. All training samples and test sample images must be processed in this way.

%Example52Tr
clear all;
load E52PT p t;
%establish BP network
pr(1:256,1)=0;
pr(1:256,1)=0;
pr(1:256,2)=1;
net=newff(pr,[251],{'logsig' 'purelin'},'traingdx','learngdm');
%Set training parameters and training BP network
net.trainParam.epochs=2500;
net.trainParam.goal=0.001;
net.trainParam.show=10;
net.trainParam.lr=0.05;
net=train(net,p,t);
%Store post training BP network
save E52net net;

The results show that

1. Construct BP neural network. The number of input nodes is 16 * 16 = 256, the hidden layer transfer function is sigmoid function (logsig), an output node, the output transfer function is pureline(purelin), and the number of hidden layer nodes is sqrt(256+1)+a(a=1~10), which is taken as 25. The learning method adopts the steepest descent method.

%Example52Sim
clear all;
p(1,256,1)=1;
p1=ones(16,16);
load E52net net;
test=input('Please input a test image:','s');
x=imread(test,'bmp');
bw=im2bw(x,0.5);
[i,j]=find(bw==0);
imin=min(i);
imax=max(i);
jmin=min(j);
jmax=max(j);
bw1=bw(imin:imax,jmin:jmax);
rate=16/max(size(bw1));
bw1=imresize(bw1,rate);
[i,j]=size(bw1);
i1=round((16-i)/2);
j1=round((16-j)/2);
p1(i1+1:i1+i,j1+1:j1+j)=bw1;
p1=-1.*p1+ones(16,16);
for m=0:15
   p(m*16+1:(m+1)*16,1)=p1(1:16,m+1);
end
[a,Pf,Af]=sim(net,p);
imshow(p1);
a=round(a)

The results show that

8, Analysis of experimental results:

As above, the program can well realize the handwritten numeral recognition function.