catalogue
2. Introduce my understanding of the implementation of prim algorithm code in books
3. If you want the source code, look directly here
1. Topic introduction
After finishing, I lost several hairs. It is estimated that nearly 200 lines of code were written. As a result, I submitted it to the OJ system and said that it was not completely right. I really can't see what went wrong with such a long code
Come and help me find out what's wrong, woo woo (the example given in the title can be output without error. I don't know where there's still a problem...)
Let's start with the topic , It is convenient to understand and reflect the algorithm more intuitively
Title Description
Creates an undirected net based on input. Prim algorithm and Kruskal algorithm are used to construct the minimum spanning tree. (assume that the minimum spanning tree of input data is unique.)
Input:
Number of vertices n
n vertices
Number of sides m
m edge information, format: vertex 1 Vertex 2 weight
Starting point of Prim algorithm v
Output:
Output the sum of the weights of the minimum spanning tree
For the two algorithms, the edge information is output according to the growth order of the tree (the edge vertices in Kruskal are output in ascending order of the array number)
sample input
6
v1 v2 v3 v4 v5 v6
10
v1 v2 6
v1 v3 1
v1 v4 5
v2 v3 5
v2 v5 3
v3 v4 5
v3 v5 6
sample output
15
prim:
v1 v3 1
v3 v6 4
v6 v4 2
v3 v2 5
v2 v5 3
kruskal:
v1 v3 1
v4 v6 2
v2 v5 3
v3 v6 4
v2 v3 5
One topic covers two algorithms, and also completes the construction of adjacency matrix
It's mainly the prim algorithm. It's really hard to understand what's in the books. I really follow my own ideas step by step, and then do it in combination with what's in the books
I can only understand the book (big talk data structure) Code meaning of
------------------------------------------------------------------------------------------------
2. Introduce my understanding of the implementation of prim algorithm code in books
Let's talk about prim algorithm first, and put the function of prim part
void prim(int** Map, int vnum, int s, int Enum, string* vertax) {
edgeifo* primEdge = new edgeifo[vnum - 1]; //It is used to store the boundary information of prim algorithm at the time of output
int locate = 0;//The primedge above the tag store
int* lowcost = new int[vnum];//Save all path weights between related vertices
int* adjvex = new int[vnum];//Save the vertex corresponding to the weight of the relevant path
int sum = 0, cal = 0;
int row = s;
for (int i = 0; i < vnum; i++)
{
lowcost[i] = Map[row][i]; // Assign all path weights of the starting point to lowcast
adjvex[i] = s;
}
while (cal++ < vnum - 1) {
int min = infinity;
for (int i = 0; i < vnum; i++) //Find the column where the minimum value is located
{
if (lowcost[i] != 0 && lowcost[i] < min)
{
min = lowcost[i];
row = i;
}
}
sum += min;
//Store the currently generated information (in fact, it can be output here, but it is affected by the subject requirements)
primEdge[locate].head = vertax[adjvex[row]];
primEdge[locate].tail = vertax[row];
primEdge[locate].power = min;
locate++;
//cout << vertax[adjvex[row]] << ' '<<vertax[row] <<" " <<min<< endl;
lowcost[row] = 0;//Indicates that the task has been completed at this point
for (int i = 0; i < vnum; i++) // Assign the vertex row data of the minimum value to lowcast
{
if (lowcost[i] != 0 && Map[row][i] < lowcost[i]) {
lowcost[i] = Map[row][i];
adjvex[i] = row; //Used to indicate which point the weight of the position comes from
}
}
}
}1. Function of lowcast array
The general principle of prim algorithm is actually well understood, that is, starting from the current point, list all path weights of the current point (this is equivalent to listing all elements of this row in the adjacency matrix, that is, put them in the lowcast array),
After listing, find the minimum value min, then go to the next point (that is, get a new row), and then get all the path weights of the next point. Note that at this time, the unexplored path of the previous point should be included (I think the code here is very clever)
How to implement the previous step in code,
Every time you go to a new point, that is, to a new row of the adjacency matrix, traverse all the elements of the row, corresponding to the array in lowcast
For each element in the, if the element of the new row corresponding to the new point is larger than the element of the current lowcast, replace it. So
You can keep the path in the original point. Of course, if each element in the new line is larger than the corresponding lowcast element
Small, then all the paths of the original points will be replaced, which is very flexible.
2. Function of adjvex array
I think this array is the most abstract and difficult to understand. I didn't understand it when I knocked it according to the code idea at the beginning
What exactly does adjvex stand for (useful is definitely useful, but I can't figure out what role it plays)
So I wrote a prim algorithm according to my own understanding, and found that I couldn't use the array of adjvex at all. I thought at the beginning
It's so simple. Hee hee, after inputting the sample, I was stupid and didn't understand why I reported an error.
In the following while loop code, you can see that row changes its value every time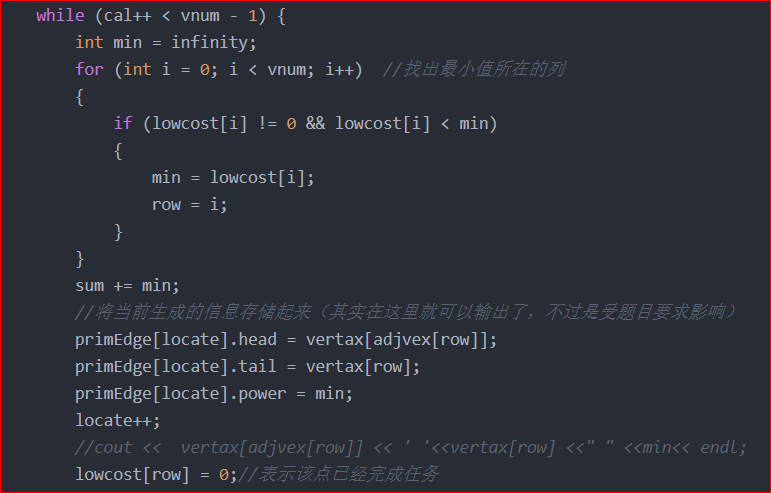
If you can understand the code here, you will know that row will change in the middle because of the change of the minimum value min, that is, at the beginning of each cycle, row refers to the original vertex, and after the for cycle, when the minimum value is found, row will change, that is, the next new vertex to go, Well, I think the row I want to output is the row at the beginning and the row after the update
So I output in this way. As a result, some vertices are wrong. The initial row is often not what I want. If I output in my way, the first point in the fourth line of the following output example should be v4, but the actual output is v3. I can't figure it out
v1 v3 1
v3 v6 4
v6 v4 2
v4 v2 5
v2 v5 3
Later, I thought over my code ideas again before I finally understood the meaning of the adjvex array. This array is used to solve the above problems. According to my above practice, I can only go to black and output continuously. For example, the output vertex of one line must be the input vertex of the next line, but it is not necessarily the case in practice, because I said earlier
Finding the next point does not mean that the original unexplored paths can be removed, and I made this mistake
And don't know it, so adjvex comes in handy at this time hhhh
for (int i = 0; i < vnum; i++) // Assign the vertex row data of the minimum value to lowcast
{
if (lowcost[i] != 0 && Map[row][i] < lowcost[i]) {
lowcost[i] = Map[row][i];
adjvex[i] = row; //Used to indicate which point the weight of the position comes from
}
}In fact, only here in the prim algorithm needs to assign a value to adjvex. In fact, this is to tell you what the current path is
If the new path is not overwritten, will the current adjvex keep the path
With the information of the original point
Therefore, when outputting data, I only need to make some changes. Originally, I used row as the input vertex at the beginning of the whole big cycle, but now
Change to the vertex corresponding to adjvex, and the subsequent output vertex is also the row after being updated. This is done
Although there are so many BBS above, I still don't think anyone can understand what I'm talking about. I'll try to make it clear when I'm free
However, the prim algorithm does not have many steps, but the code is abstract and difficult to understand. I deduce it according to my own ideas
I think it is very helpful to understand prim algorithm
-----------------------------------------------------------------------------------------------
-------------------------------------------------------
3.kruskal algorithm
kruskal algorithm is relatively intuitive and easy to understand. The code implementation is simpler than prim. My code is also encapsulated with functions.
kruskal arranges the weights of all edges from small to large from a God's perspective, and then selects the path from small to large
The sample can well construct the minimum spanning tree of the graph. It should be noted that a Find function needs to be written to determine whether a loop will be formed and lead
To build is not a minimum spanning tree
3. If you want the source code, look directly here
#include<iostream>
#include<cstring>
using namespace std;
#define infinity 65535;
typedef struct edgeifo
{
string head;
string tail;
int power;
};
int** MakeGraph(int num, int Enum, string* vertax, edgeifo* edge, char Gtype)
{
int** matrix = new int* [num]; //Open up space
for (int i = 0; i < num; i++)
{
matrix[i] = new int[num];
for (int j = 0; j < num; j++)
{
if (i == j)
matrix[i][j] = 0;
else
matrix[i][j] = infinity; //Initialize array
}
}
for (int j = 0; j < Enum; j++)
{
int row, column;
for (int i = 0; i < num; i++)
{
if (vertax[i] == edge[j].head)
{
row = i;
}
}
for (int i = 0; i < num; i++)
{
if (vertax[i] == edge[j].tail)
{
column = i;
}
}
matrix[row][column] = edge[j].power;
if (Gtype == 'U')
matrix[column][row] = edge[j].power;
}
//Output the array
return matrix;
}
void prim(int** Map, int vnum, int s, int Enum, string* vertax) {
edgeifo* primEdge = new edgeifo[vnum - 1]; //It is used to store the boundary information of prim algorithm at the time of output
int locate = 0;//The primedge above the tag store
int* lowcost = new int[vnum];//Save all path weights between related vertices
int* adjvex = new int[vnum];//Save the vertex corresponding to the weight of the relevant path
int sum = 0, cal = 0;
int row = s;
for (int i = 0; i < vnum; i++)
{
lowcost[i] = Map[row][i]; // Assign all path weights of the starting point to lowcast
adjvex[i] = s;
}
while (cal++ < vnum - 1) {
int min = infinity;
for (int i = 0; i < vnum; i++) //Find the column where the minimum value is located
{
if (lowcost[i] != 0 && lowcost[i] < min)
{
min = lowcost[i];
row = i;
}
}
sum += min;
//Store the currently generated information (in fact, it can be output here, but it is affected by the subject requirements)
primEdge[locate].head = vertax[adjvex[row]];
primEdge[locate].tail = vertax[row];
primEdge[locate].power = min;
locate++;
//cout << vertax[adjvex[row]] << ' '<<vertax[row] <<" " <<min<< endl;
lowcost[row] = 0;//Indicates that the task has been completed at this point
for (int i = 0; i < vnum; i++) // Assign the vertex row data of the minimum value to lowcast
{
if (lowcost[i] != 0 && Map[row][i] < lowcost[i]) {
lowcost[i] = Map[row][i];
adjvex[i] = row; //Used to indicate which point the weight of the position comes from
}
}
}
//output
cout << sum << endl << "prim:" << endl;
for (int i = 0; i < vnum - 1; i++)
{
cout << primEdge[i].head << " " << primEdge[i].tail << " " << primEdge[i].power << endl;
}
}
int Find(int* parent,int f) {
while (parent[f] > 0) {
f = parent[f]; //Keep looking for points that have not been connected
}
return f;
}
void kruskal(int** Map, int vnum, int Enum ,edgeifo* edge,string* vertax) {
//Get the edge set array first
cout << "kruskal:" << endl;
edgeifo* Earr = new edgeifo[Enum];
memcpy(Earr, edge, sizeof(struct edgeifo)*Enum);//Copy structure array
for (int i = 0; i < Enum - 1; i++) //Sort by weight from small to large
{
for (int j = 0; j < Enum - i -1; j++)
{
if (Earr[j].power > Earr[j + 1].power) {
edgeifo tp;
tp = Earr[j];
Earr[j] = Earr[j + 1];
Earr[j + 1] = tp;
}
}
}
int* parent = new int[Enum]; //It is used to store boundary information and judge whether a loop is formed
for (int i = 0; i < Enum; i++)
{
parent[i] = 0; //initialization
}
for (int i = 0; i < Enum; i++) //Traverse each edge
{
int begin, end;
for (int j = 0; j < vnum; j++)
{
if (Earr[i].head == vertax[j])
begin = j;
if (Earr[i].tail == vertax[j])
end = j;
}
int m, n;
n = Find(parent,begin);
m = Find(parent,end);
if (n != m)
{
parent[n] = m; //Indicates that the nth vertex is connected with the m vertex
cout << Earr[i].head << ' ' << Earr[i].tail << ' ' << Earr[i].power << endl;
}
}
}
void MatrixIfo(int num, char Gtype) {
int Enum; string* vertax = new string[num];
//cout << "please enter each vertax :" << endl
//Input vertex
for (int i = 0; i < num; i++)
{
cin >> vertax[i];
}
//cout << "enter the edge number:" << endl;// Enter the number of edges and information
cin >> Enum;
edgeifo* edge = new edgeifo[Enum];
for (int i = 0; i < Enum; i++) {
cin >> edge[i].head;
cin >> edge[i].tail;
cin >> edge[i].power;
}
string start; int startNum;
cin >> start;
for (int i = 0; i < num; i++)
{
if (start == vertax[i])
startNum = i;
}
//Boundary information input completed
//Return adjacency matrix
int** Map = MakeGraph(num, Enum, vertax, edge, Gtype);
prim(Map, num, startNum, Enum, vertax); //prim algorithm
kruskal(Map, num, Enum,edge,vertax); //kruskal Algorithm
}
int main() {
char Gtype = 'U';//Directly indicate that it is an undirected graph
int num;
cin >> num;
MatrixIfo(num, Gtype);
}
Rookies write questions and don't like welcome spray