What is the fast power of a matrix?
- Fast power is a fast method to solve the power of a number by using binary.
The principle of fast power will be briefly explained later. If you still don't understand it, please Baidu yourself.
I believe that many young friends are new to college and may not have studied linear algebra (such as me), so they almost don't know what matrix is. I recommend a website to see how matrix multiplication works. Here is the website link: (how to this website is really a cow. There are tutorials on everything, and the quality is high! 😂)
Calculation method of matrix multiplication
So how to use code to represent the matrix and its multiplication?
In fact, it is very simple, that is, three-layer cycle control.
For example, here is the overloaded operator of C + +. Matrix is a class defined by me.
Matrix& operator*(Matrix& b){
assert(b.date!=NULL && date!=NULL && m==b.n);
ll tmp[n][b.m];
for(int i=0;i<n;i++){
for(int j=0;j<b.m;j++){
ll sum = 0;
for(int k=0;k<m;k++){
sum = (sum + date[i][k]*b.date[k][j])%MOD;
}
tmp[i][j] = sum;
}
}
this->m = b.m;
for(int i=0;i<n;i++){
for (int j = 0; j < m; ++j) {
date[i][j] = tmp[i][j];
}
}
return *this;
}
How to calculate the fast power of matrix?
About how to fast power a matrix, let's first look at the simple fast power.
Fast power is to realize fast same number multiplication through bit operation.
Briefly describe the principle of fast power:
The principle is that if the third power of X is required, it can be transformed into the second power of x*x, and it is very simple to find the 2^n power of a number. For example, if x *= x once, we will get the quadratic power of X. if x *= x again, we will get the fourth power, and if we continue, we can get 8 / 16... In short, it is the time of log2N.
The code is as follows:
int QuickPow(int x,int n){
int c = n;
int res = 1;
while(c!=0){
if(c&1!=0){
res *= x;
}
c >>= 1;
x *= x;
}
return res;
}
- So how does the fast power of the matrix proceed?
Replacing the above int type with a self-defined matrix is the fast power of the matrix.
I directly pasted the fast power writing method of the class after the overloaded operator implemented in C + +:
quickPow here represents a member function of a class, so you can directly use the data in this matrix for operations. This represents the pointer to this object. init() member function represents initialization to the identity matrix.
void quickPow(ll c){
if(c==1||c<0)return;
if(c==0){
init();
return;
}
Matrix tmp(*this);
init();
while (c){
if(c&1){
*this = *this * tmp;
}
c >>= 1;
tmp = tmp*tmp;
}
}
Why do you suddenly want to write this template?
It's mainly because I recently did several fast power problems, and I was badly hurt. Then I suddenly wanted to design a template, mainly my_tiny_stl This warehouse hasn't been updated for a long time 😂
subject
How did I get trapped
- First, I got this question, and I immediately started to implement the simple O(n) recursive method, then submitted it, and then timed out..
When I fixed my eyes, the amount of data turned out to be so large!
After thinking about it, it must be the fast power of the matrix. First come up with the recursive formula of the following matrix:
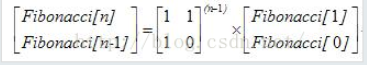
Then the problem can be solved.
Then I simply encapsulated a matrix class with C + + classes, which overloaded the multiplication and quickpow methods, and then leisurely prepared to submit. Before submitting, I encountered the syntax traps of C + +
Syntax trap (non-C + + party detour recommended)
Because classes use heap memory, I wrote destructors. The problem I encountered was that when I overloaded multiplication, I returned an lvalue, and I did not overload '=', so '=' is a direct copy of member variables. As a result, the date s of the two objects point to the same memory space, and the previous memory space is leaked, and The latter two objects will certainly call the destructor, which leads to the destructor calling twice!
- How to solve this problem? If it is C++98, this problem is very big. Basically, there are two methods to solve it:
- To avoid the problem, the left operand of multiplication must be the current assignment object, so as to avoid the direct change of the pointer in the original object by the last assignment statement.
- The most direct way to solve this kind of problem, whether C++11 or C++98, is to overload the '=' number. The implementation of the overload '=' number is carried out according to the specific situation. For the specific implementation of the overload of assignment, we need to consider two things: first, we need to reduce the application and use of memory as much as possible (specifically, judge whether the pointers of two objects point to the same space, even if they are not the same space. In order to increase space utilization, you can also judge whether the two spaces are the same size, and then copy). Second, if it is a temporary object, you need to set its pointer to null (prevent the compiler from not optimizing the destructor of temporary variables, so that the destructor is called to destruct the same memory multiple times).
- Since C++11 began to have the right value reference and its supporting mobile assignment constructor, it can directly call the temporary variable to the mobile constructor into a named object, and then operate. Generally, it is to transfer its pointer ownership, and then set its pointer to null to prevent parsing errors. In my understanding, the emergence of right value reference is to capture anonymous objects After that, the appropriate performance optimization operation is given to the programmer. Before there is no right value reference, the memory of the anonymous object can not be used at all. It can only be used after simple assignment and copy operation, which consumes memory. After the right value reference appears, we can capture the anonymous object through the right value reference, and then operate its underlying memory. There is also a big problem Memory related updates have a nullptr keyword, which makes null pointers no longer ambiguous, so delete nullptr is safe. Therefore, to prevent errors from deleting the same space multiple times, you can assign it nullptr.
- So how to solve the problem based on C++11? The solution is just as good as C++98, which is more convenient for memory management. If there is an R-value on the right of the equal sign, it must be a temporary object, so we can directly use its memory in the overload of '=' and set its pointer to null. If there is no R-value type For line capture, the compiler will also optimize temporary objects by default, and can prevent the generation of assignment copies of multiple objects, but it can only be optimized during object initialization! At other times, the destructor will still be called. At this time, if the '=' overload generated by the compiler by default will be used, the pointer of the space to be parsed will be assigned, The assignment overload of our R-value reference version is aimed at this phenomenon. In this way, it is convenient for memory management to separate the R-value and l-value. The R-value is a temporary variable, which only takes a while, so it can directly take its memory to continue to use without affecting the program logic. The l-value is different, and it still needs to survive for a long time, so I We need to create another space to copy.
Special reminder: if you are doing algorithm problems, you don't need to consider memory management at all, and don't write destructors. After all, you only need a single call, and the object can exist for a while at most.
Problem trap
Don't be reluctant to open long long when necessary!!!!
The data quantity of this problem, whether to the power of power or the data of the whole recording process, should be long long!!!
I've been trapped by this trap countless times, and this time it's no different 😅
After I started writing this class, I passed the first five, and then the last five reported errors. I thought there was a problem with the class I designed, and I specially wrote several ordinary C language versions 😂 Finally, I found that the old one didn't open long long. The following is the code version after changing long long. I wrote several versions with macro definitions...
The design of this Matrix class is still not considered in place in many places. For example, the problem of the previous trap is only solved through method 1 without overloading the assignment operator... So learn from the past and design a more available Matrix class!
- The efficiency is fast and slow, which mainly depends on whether the compiler is optimized.

//
// Created by Alone on 2021/11/19.
//
#include <bits/stdc++.h>
using namespace std;
//#define ELSE_MAIN
#define MY_MAIN
#define MAT
#ifdef MAT
typedef long long ll;
class Matrix{
ll** date;
int m;
int n;
public: static const int MOD;
public:
Matrix(ll** rec,int n,int m):date(rec),n(n),m(m){}//C style initialization
Matrix():date(NULL),m(0),n(0){} //default
Matrix(Matrix& b):n(b.n),m(b.m){//copy construction
assert(b.date!=NULL && b.n>0 && b.m>0);
date = new ll*[n];
copy(b.date,b.date+n,date);
for(int i=0;i<n;i++){
date[i] = new ll[m];
copy(b.date[i],b.date[i]+m,date[i]);
}
}
~Matrix(){//Destructor implementation
assert(date!=NULL && n>0 && m>0);
for (int i = n-1; i >=0 ; --i) {
delete [] date[i];
}
delete[] date;
}
Matrix& operator*(Matrix& b){
assert(b.date!=NULL && date!=NULL && m==b.n);
ll tmp[n][b.m];
for(int i=0;i<n;i++){
for(int j=0;j<b.m;j++){
ll sum = 0;
for(int k=0;k<m;k++){
sum = (sum + date[i][k]*b.date[k][j])%MOD;
}
tmp[i][j] = sum;
}
}
this->m = b.m;
for(int i=0;i<n;i++){
for (int j = 0; j < m; ++j) {
date[i][j] = tmp[i][j];
}
}
return *this;
}
void init(){//Reinitialize to identity matrix
assert(date!=NULL && n>0 && m>0);
for (int i = 0; i < n; ++i) {
for (int j = 0; j < m; ++j) {
if(i==j)date[i][j] = 1;
else date[i][j] = 0;
}
}
}
void quickPow(ll c){
if(c==1||c<0)return;
if(c==0){
init();
return;
}
Matrix tmp(*this);
init();
while (c){
if(c&1){
*this = *this * tmp;
}
c >>= 1;
tmp = tmp*tmp;
}
}
void print(){
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
cout<<date[i][j]<<' ';
}
cout<<endl;
}
}
int get(int x,int y){
assert(date!=NULL && x<n && y<m);
return date[x][y];
}
};
const int Matrix::MOD = 1e9+7;
#endif
#ifdef MY_MAIN
int main(){
ll c;
cin>>c;
ll** matrix = new ll*[2];
matrix[0] = new ll[2]{1,1};
matrix[1] = new ll[2]{1,0};
Matrix mat(matrix,2,2);
mat.quickPow(c-1);
//mat.print();
ll** res = new ll*[2];
res[0] = new ll[1];
res[1] = new ll[1];
res[0][0] = res[1][0] = 1;
Matrix fib(res,2,1);
//There is a memory allocation error. mat*fib returns an lvalue, while = does not overload the default direct assignment member variable.
//As a direct result, fib loses its previous variable ownership and shares a memory space with mat, resulting in the same space being free twice
//Overload the = sign to prevent rebinding the same piece of memory without releasing the direct memory
Matrix ret(mat*fib);
cout<<ret.get(0,0);
return 0;
}
#endif
#ifdef TEST_MAIN
typedef long long ll ;
const int MOD = 1e9+7;
ll a[2][2]{{1,1},{1,0}};ll b[2]{1,1};
void selfMut(){
ll tmp[2][2];
for(int i=0;i<2;i++){
for(int j=0;j<2;j++){
ll sum = 0;
for(int k=0;k<2;k++){
sum = (sum+a[i][k]*a[k][j])%MOD;
}
tmp[i][j] = sum;
}
}
for(int i=0;i<2;i++){
memmove(a[i],tmp[i],sizeof(tmp[i]));
}
}
void difMut(){
ll tmp[2];
for(int i=0;i<2;i++){
ll sum = 0;
for(int k=0;k<2;k++){
sum = (sum + a[i][k]*b[k])%MOD;
}
tmp[i] = sum;
}
b[0] = tmp[0];
b[1] = tmp[1];
}
void Mut(ll _a[2][2],ll _b[2][2],int n1,int m1,int n2,int m2){
if(m1!=n2)
return ;
int tmp[n1][m2];
for(int i=0;i<n1;i++){
for(int j=0;j<m2;j++){
ll sum = 0;
for(int k=0;k<m1;k++){
sum = (sum+_a[i][k]*_b[k][j])%MOD;
}
tmp[i][j] = sum;
}
}
for(int i=0;i<n1;i++){
for(int j=0;j<m2;j++){
_a[i][j] = tmp[i][j];
}
}
}
void quickPow(int k){
ll tmp[2][2]{{1,0},{0,1}};
while (k){
if(k&1){
Mut(tmp,a,2,2,2,2);
}
k>>=1;
selfMut();
}
for(int i=0;i<2;i++){
memmove(a[i],tmp[i],sizeof(tmp[i]));
}
}
int main(){
int c;
cin>>c;
quickPow(c-1);
for(int i=0;i<2;i++){
for(int j=0;j<2;j++){
printf("%d ",a[i][j]);
}
cout<<endl;
}
difMut();
cout<<b[0];
}
#endif
#ifdef ELSE_MAIN
const long long int p = 1000000007;
struct Mat
{
long long int m[2][2];
};
Mat ans, base;
Mat Mul(Mat x, Mat y)
{
Mat c;
for(int i = 0; i < 2; i++)
{
for(int j = 0; j < 2; j++)
{
c.m[i][j] = 0;
for(int k = 0; k < 2; k++)
{
c.m[i][j] = (c.m[i][j] + x.m[i][k] * y.m[k][j]) % p;
}
}
}
return c;
}
int Qpow(long long int n)
{
for(int i = 0; i < 2; i++)
{
for(int j = 0; j < 2; j++)
{
if(i == j)
{
ans.m[i][j] = 1;
}
else
{
ans.m[i][j] = 0;
}
if(i == 1 && j == 1)
{
base.m[i][j] = 0;
}
else
{
base.m[i][j] = 1;
}
}
}//In this section, in order to initialize ans as an identity matrix, initialize base as a matrix of the required n-power
while(n)
{
if(n & 1)
{
ans = Mul(ans, base);
}
base = Mul(base, base);
n >>= 1;
}
return ans.m[0][0];
}
int main()
{
long long int n = 0;
cin >> n;
cout << Qpow(n);
return 0;
}
#endif
Teach you to design Matrix classes
How to design a class?
Structure:
- Internal data abstraction: operation data storage of objects
- The two-level pointer date is used for memory management of the two-dimensional space of the matrix, and n and m represent the row height and column width of the matrix.
- Behavior abstraction: a description of the behavior of an object
- Constructor (default, custom, copy, move) and destructor (call destory member function).
- Setters and getter s. Provide function interface to set and get data.
- Function functions: for example, overloaded multiplication operators and fast power functions are all function functions.
Property abstraction of object:
- Whether the data and behavior are external or not. The significance of encapsulating data externally is to prevent the destruction of the object behavior description. A behavior that is open to the outside world usually requires repeated calls from multiple internal functions. At this time, the public and private keywords need to be used for modification.
- Whether the data and behavior can be inherited. For some behaviors (functions), we don't want to be called externally, but it is very useful for subclasses. At this time, we can use the protect keyword to modify them.
- Whether the data and behavior can be reused. In order to save unnecessary memory overhead, general functions that do not need to generate specific objects can be designed and modified with the static keyword. This can avoid that I have to apply for a piece of irrelevant memory space before I want to use a function, and the data of an object can also be modified with static, In this way, the data does not need to be applied and assigned during the creation of the object.
Next, let's determine the properties of the behavior (function). The data must not be private, otherwise object-oriented will be meaningless.
- Constructors and destructors are the key to the creation and destruction of objects, so if you don't want objects not to be created or destroyed, you should use public decoration.
- Setters and getter s. Obviously, it is an open interface function, so it must also be a public modification.
- Function function: matrix fast power function. Obviously, we want to set a general-purpose case. At this time, it should be called without creating an object, so it's best to modify it with static (this is generally an external general-purpose interface, and a convenient class calling version needs to be implemented internally, which is also very simple. Just call the function by directly passing parameters), Overloaded multiplication must also be external, so it needs public modification. The destroy function is used to deal with memory recycling. Obviously, this is an internal general function, but the outside world doesn't need it at all! So set it to the private property.
The above is the design idea of the whole class. Of course, when you really design, you also need to be specific to the function parameters and return value types, because this involves the specific syntax of C + +. For example, what type should I return when overloading multiplication? It is best to return an R-value! The overloaded assignment operator is better to return an lvalue. Generally, when considering the choice of return value type, the most difficult thing is whether I should return an l-value or an R-value if I return an object.
After writing C + + for so long, I feel that the feature of Java shielding overloaded operators written in C + + is that there are too many processes to consider when overloading operators. C + + chicken (I'm a rookie) 😂) Write extremely inefficient and unsafe code, and only old birds can write elegant and efficient code.
Concrete abstract structure of class (concrete planning diagram of code)
Each part of the class is classified according to attributes. After all, attributes basically represent the usage scenario of this method.
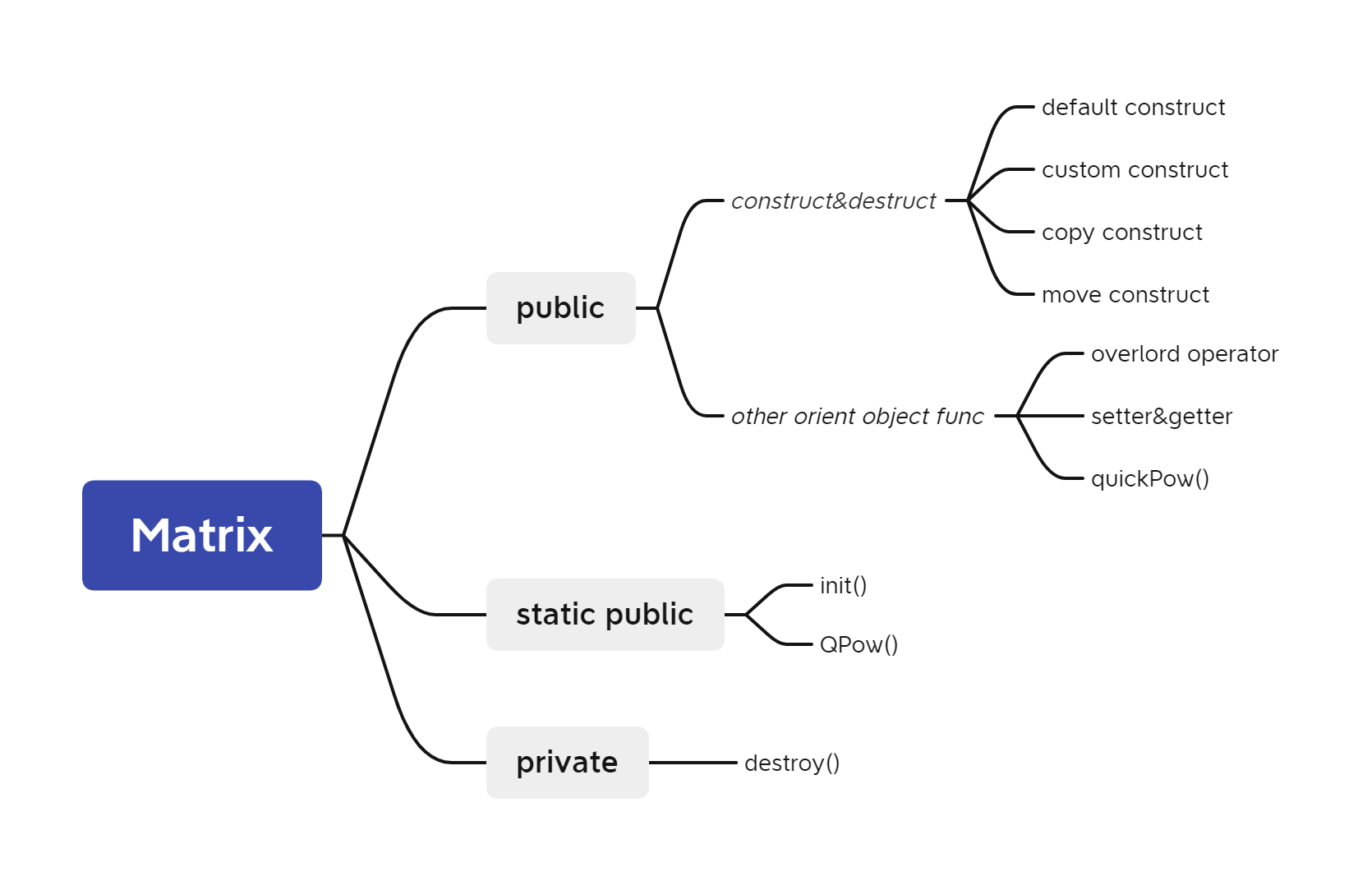
- Finally, basic assertions or exceptions can be used to make the code more robust, making it easier to locate the location and cause of the error.
Implementation matrix generic template class
Source code implementation
I first draw a plan for implementation, and then in the process of implementation, I find that some features can be added, such as overloading the subscript operator, such as printing it with the print function for verification.
In the specific implementation process, in order to easily locate possible errors, a large number of assertions are used for assertion checking. If you want to make the code more robust, you can use the method of throwing exceptions.
GitHub warehouse address corresponding to source code: Warehouse link, and the implementation of more templates, including a small amount of STL
Better source code reading experience: Source code online reading
It is not easy to read the following code directly. It is recommended to check the source code in GitHub1s above.
//
// Created by L_B__ on 2021/11/20.
//
#ifndef LQTEST_MATRIX_H
#define LQTEST_MATRIX_H
#include <cassert>
#include <algorithm>
#include <iostream>
#define _MOD
template<typename T>
class Matrix {
/*Type define*/
typedef T data_t;
typedef int ssize_t;
/*data source*/
data_t **data;
ssize_t n;
ssize_t m;
public:
static const data_t MOD;
public:
/*default construct*/
Matrix() : m(0), n(0), data(nullptr) {}
/*custom construct*/
Matrix(data_t **mat, ssize_t n, ssize_t m) : data(mat), n(n), m(m) {}//External request memory passed into internal
Matrix(ssize_t n, ssize_t m) : data(nullptr), n(n), m(m) {//You can specify the rows and columns of the matrix externally, and the memory initialization is performed internally
assert(n > 0 && m > 0);
data = new data_t *[n];
for (int i = 0; i < n; i++) {
data[i] = new data_t[m];
}
init(data, n, m);
}
/*copy construct*/
Matrix(Matrix &src) : data(nullptr), n(src.n), m(src.m)//Const & reference type can also be used, but in this way, many right value cases will not call the move construct
{
assert(n > 0 && m > 0);
data = new data_t *[n];
for (int i = 0; i < n; ++i) {
data[i] = new data_t[m];
std::copy(src.data[i], src.data[i] + m, data[i]);
}
}
/*move construct*/
Matrix(Matrix<data_t> &&src) : n(src.n), m(src.m), data(nullptr) {
assert(src.data != nullptr && n > 0 && m > 0);
data = src.data;
src.data = nullptr;
src.n = src.m = 0;
}
/*destruct*/
~Matrix() {
destroy();
}
/*overload*/
//Plus a special version of MOD
#ifdef _MOD
Matrix operator*(const Matrix<data_t> &src)//It is recommended to return the right value. There are many subsequent pits that return the left value. The parameter const & can accept both the left value and the right value
{
assert(data != nullptr && src.data != nullptr && m == src.n && m > 0 && n > 0 && src.m > 0);//Necessary conditions for matrix multiplication
data_t **tmp = new data_t *[n]; //Request dynamic memory for tmp because it is an outgoing parameter
for (int i = 0; i < n; ++i) {
tmp[i] = new data_t[m];
}
for (int i = 0; i < n; ++i)//Start updating tmp
{
for (int j = 0; j < src.m; ++j) {
data_t sum = 0;
for (int k = 0; k < m; ++k) {
sum = (sum + data[i][k] * src.data[k][j]) % MOD;
}
tmp[i][j] = sum;
}
}
//Directly construct anonymous object return
return Matrix(tmp, n, src.m);;
}
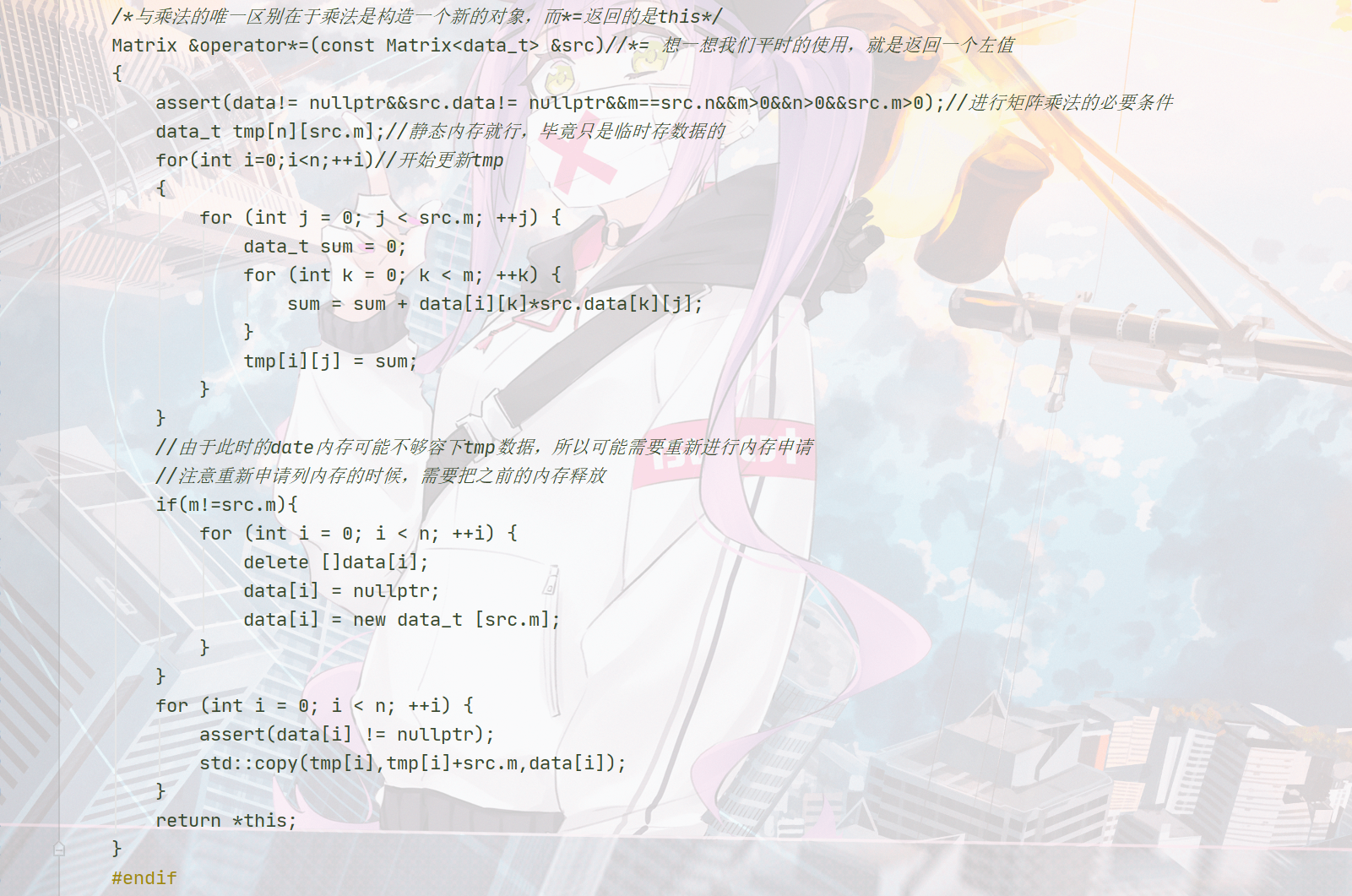
Matrix &operator*=(const Matrix<data_t> &src)//*=Think about our usual use, which is to return an lvalue
{
assert(data != nullptr && src.data != nullptr && m == src.n && m > 0 && n > 0 && src.m > 0);//Necessary conditions for matrix multiplication
data_t tmp[n][src.m];//Static memory is OK. After all, it is only used to store data temporarily
for (int i = 0; i < n; ++i)//Start updating tmp
{
for (int j = 0; j < src.m; ++j) {
data_t sum = 0;
for (int k = 0; k < m; ++k) {
sum = (sum + data[i][k] * src.data[k][j]) % MOD;
}
tmp[i][j] = sum;
}
}
//Since the date memory may not be enough for tmp data at this time, it may be necessary to re apply for memory
//Note that when re applying for column memory, you need to release the previous memory
if (m != src.m) {
for (int i = 0; i < n; ++i) {
delete[]data[i];
data[i] = nullptr;
data[i] = new data_t[src.m];
}
}
for (int i = 0; i < n; ++i) {
assert(data[i] != nullptr);
std::copy(tmp[i], tmp[i] + src.m, data[i]);
}
return *this;
}
#endif
#ifndef _MOD
Matrix operator*(const Matrix<data_t>&src)//It is recommended to return the right value. There are many subsequent pits that return the left value. The parameter const & can accept both the left value and the right value
{
assert(data!= nullptr&&src.data!= nullptr&&m==src.n&&m>0&&n>0&&src.m>0);//Necessary conditions for matrix multiplication
data_t** tmp = new data_t *[n]; //Request dynamic memory for tmp because it is an outgoing parameter
for (int i = 0; i < n; ++i) {
tmp[i] = new data_t [m];
}
for(int i=0;i<n;++i)//Start updating tmp
{
for (int j = 0; j < src.m; ++j) {
data_t sum = 0;
for (int k = 0; k < m; ++k) {
sum = sum + data[i][k]*src.data[k][j];
}
tmp[i][j] = sum;
}
}
//Directly construct anonymous object return
return Matrix (tmp,n,src.m);
}
/*The only difference from multiplication is that multiplication constructs a new object, while * = returns this*/
Matrix &operator*=(const Matrix<data_t> &src)//*=Think about our usual use, which is to return an lvalue
{
assert(data!= nullptr&&src.data!= nullptr&&m==src.n&&m>0&&n>0&&src.m>0);//Necessary conditions for matrix multiplication
data_t tmp[n][src.m];//Static memory is OK. After all, it is only used to store data temporarily
for(int i=0;i<n;++i)//Start updating tmp
{
for (int j = 0; j < src.m; ++j) {
data_t sum = 0;
for (int k = 0; k < m; ++k) {
sum = sum + data[i][k]*src.data[k][j];
}
tmp[i][j] = sum;
}
}
//Since the date memory may not be enough for tmp data at this time, it may be necessary to re apply for memory
//Note that when re applying for column memory, you need to release the previous memory
if(m!=src.m){
for (int i = 0; i < n; ++i) {
delete []data[i];
data[i] = nullptr;
data[i] = new data_t [src.m];
}
}
for (int i = 0; i < n; ++i) {
assert(data[i] != nullptr);
std::copy(tmp[i],tmp[i]+src.m,data[i]);
}
return *this;
}
#endif
//The overload of assignment number needs to separate the left and right values to achieve copy: the deep is the deep, and the shallow is the shallow
Matrix &operator=(Matrix &src)//If the right is an lvalue, a deep copy (without copying the pointer) is required
{
assert(src.data != nullptr && src.n > 0 && src.m > 0);
destroy();//Clear memory before copying
n = src.n;
m = src.m;
data = new data_t *[n];
for (int i = 0; i < n; ++i) {
assert(data[i] != nullptr);//In fact, it is not necessary, because the bad_alloc exception will be thrown if the new application fails
data[i] = new data_t[m];
std::copy(src.data[i], src.data[i] + m, data[i]);
}
return *this;
}
Matrix &operator=(Matrix &&src)//If the right is an R-value, a shallow copy is made
{
assert(src.data != nullptr && src.n > 0 && src.m > 0);
destroy();//Clear memory before copying
n = src.n;
m = src.m;
data = src.data;
src.data = nullptr;
src.n = src.m = 0;
return *this;
}
data_t *&operator[](ssize_t i) {
assert(i >= 0 && i < n);
return data[i];
}
/*Fast implementation, object-oriented interface*/
void quickPow(data_t c) {
QPow(*this, c);
}
/*setter And getter implementation*/
void set(ssize_t x, ssize_t y, data_t src) {
assert(x >= 0 && x < n && y >= 0 && y < m);
data[x][y] = src;
}
data_t &get(ssize_t x, ssize_t y) {
//Return a reference, which can be modified directly in the outside world. Of course, the outside world should also use a reference to catch it, otherwise it is just a copy
assert(x >= 0 && x < n && y >= 0 && y < m);
return data[x][y];
}
void print() {
for (int i = 0; i < n; ++i) {
for (int j = 0; j < m; ++j) {
std::cout << data[i][j] << ' ';
}
std::cout << std::endl;
}
}
public:
static void init(data_t **data, ssize_t n, ssize_t m) {
assert(data != nullptr && n > 0 && m > 0);
for (int i = 0; i < n; ++i) {
for (int j = 0; j < m; ++j) {
if (i == j)data[i][j] = 1;
else data[i][j] = 0;
}
}
}
static void QPow(Matrix &_Dest, data_t n) {
assert(n >= 0);
Matrix tmp(_Dest);//Make a copy for multiplication
init(_Dest.data, _Dest.n, _Dest.m);//Initialize to identity matrix
if (n == 0)
return;
while (n) {
if (n & 1) {
_Dest *= tmp;
}
tmp *= tmp;
n >>= 1;
}
}
private:
void destroy() {
if (data == nullptr)
return;
for (int i = 0; i < n; i++) {
if (data[i] == nullptr)//If there is nullptr in this memory, it indicates that it has been delete d before
return;
delete[] data[i];
data[i] = nullptr;
}
delete[] data;
data = nullptr;
}
};
#endif //LQTEST_MATRIX_H
usage method
- Instructions for use: two sets of multiplication codes are implemented internally through macro definition. One set does not take the module of MOD, and the other is to take the module, but the initial value of MOD must be assigned externally first.
End use example:
We only need to care about two points: 1. The construction and initialization of matrix class 2. The use of basic member functions
1, Construction and initialization of matrix class
Because it is a template class, you need to specify the type of template
#include "Matrix.h"
//The dataType below is the data type of each element of the matrix you need, which you need to pass in yourself
int main(){
Matrix<dataType> a;//Default Constructor
Matrix<dataType> b(3,3);//Get the matrix with three rows and three columns. The default is the identity matrix
int** ret = new ...//Omitted here, in short, is to apply for two-dimensional memory
Matrix<dataType> c(ret,m,n);//The outside world applies for memory and assigns an initial value, and then initializes the class
Matrix<dataType> d(c);or Matrix d = c;//Initializing d objects with existing classes (creating new memory)
Matrix<dataType> e(c*d);or Matrix e = c*d;//Initialization through temporary objects (no new memory is created)
}
Corresponding source code:

2, Use of basic member functions
Of course, multiplication has been overloaded, so as long as the two matrices can be multiplied, the result can be obtained directly.
#include "Matrix.h"
int main(){
//Initialize a matrix as {{1,1}, {1,0}
Matrix<long long > a(2,2);
a[0][0] = a[1][0] = a[0][1] = 1;
a[1][2];
int c; cin>>c;
//Call the fast power to update the data of the matrix to the power of c
a.quickPow(c);
a[0][0];or a.get(0,0);//An element that can access the (0,0) position of a
a.print() //Print out the current value of the matrix
//For example, a is now {1,1} {1,0}
// Print:
//1 1
//1 0
}
If you want to get the fast power result of modular MOD, you need to add a macro definition _modin front of the Matrix file, and then use it as follows:
#include "Matrix.h"
template<> const long long Matrix<long long>::MOD = 1e9+7;//Initialize the value of MOD
int main(){
Matrix<long long > a(2,2);
a[0][0] = a[1][0] = a[0][1] = 1;
a[1][2];
Matrix<long long> b(2,1);
b[0][0] = b[1][0] = 1;
long long c;
std::cin>>c;
a.quickPow(c-1);
b = a*b;
std::cout<<b[0][0];
}
Corresponding source code:
MOD version:

Non MOD version:

k fast power realization: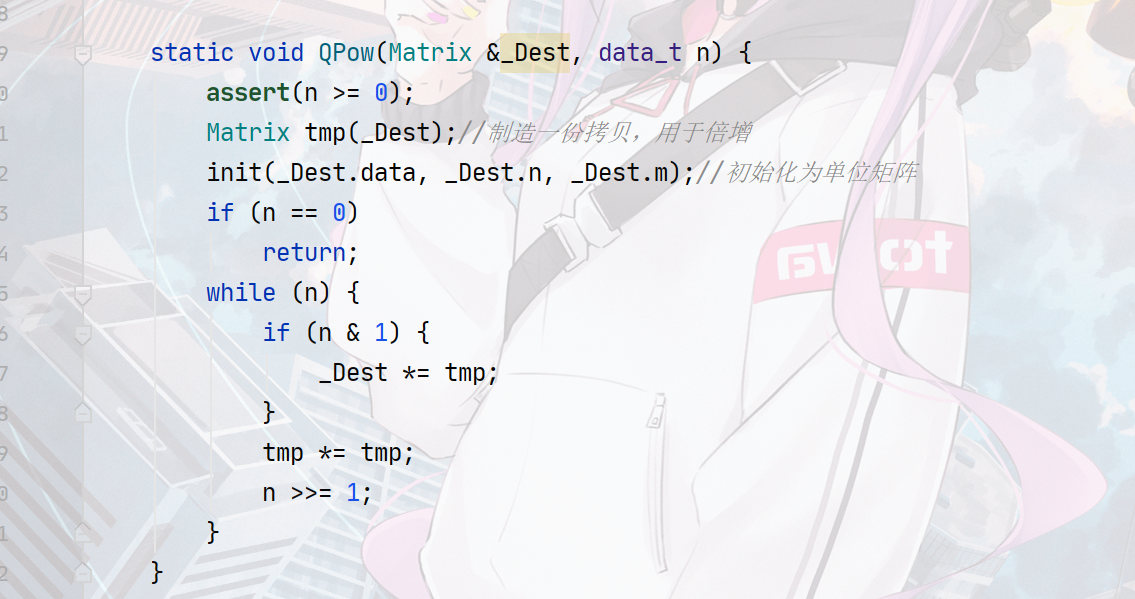

3, Problem solving verification
- Because lanqiao network does not support C++11, I directly input test cases locally for testing.
First measure a simple:

The following measurements were made:

A little bigger (it should be the limit of long long)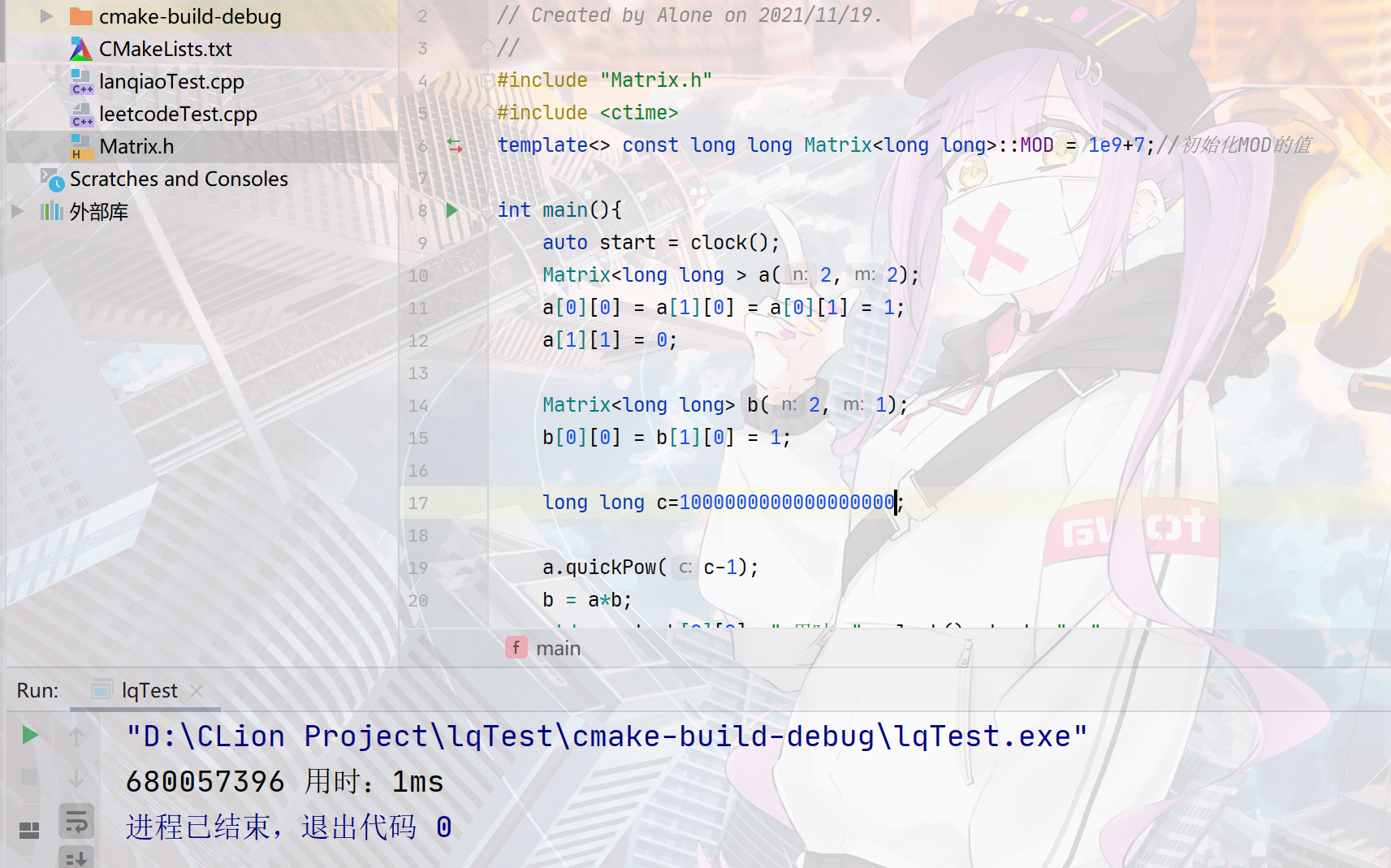
Still stable for about 1ms!!!! I can only say two words: excellent!
summary
Because it is a template class implemented with the syntax of C++11, compilers lower than this version cannot be used normally. I consulted relevant materials. In fact, C++11 can be used in the Blue Bridge Cup, and acm needless to say, C++11 can be used long ago.
Simple redo:
To implement such a class, you can mainly learn the following points:
- Class design skills.
- Have a deeper understanding of the left and right values of C + +.
- The design and implementation of various constructors have reached the level of perfection.
