sort

The concept and application of sorting

Sorting concept

==Sorting: = = the so-called sorting is the operation of arranging a string of records incrementally or decrementally according to the size of one or some keywords.
==Stability: = = if there are multiple records with the same keyword in the record sequence to be sorted, the relative order of these records remains unchanged after sorting, that is, in the original sequence, r[i]=r[j], and r[i] is before r[j], but in the sorted sequence, r[i] is still before r[j], then this sorting algorithm is said to be stable; Otherwise, it is called unstable.
==Internal sorting: = = sorting in which all data elements are placed in memory.
==External sorting: = = too many data elements can not be placed in memory at the same time. According to the requirements of sorting process, the sorting of data can not be moved between internal and external memory.

Sorting application

Come to Jingdong

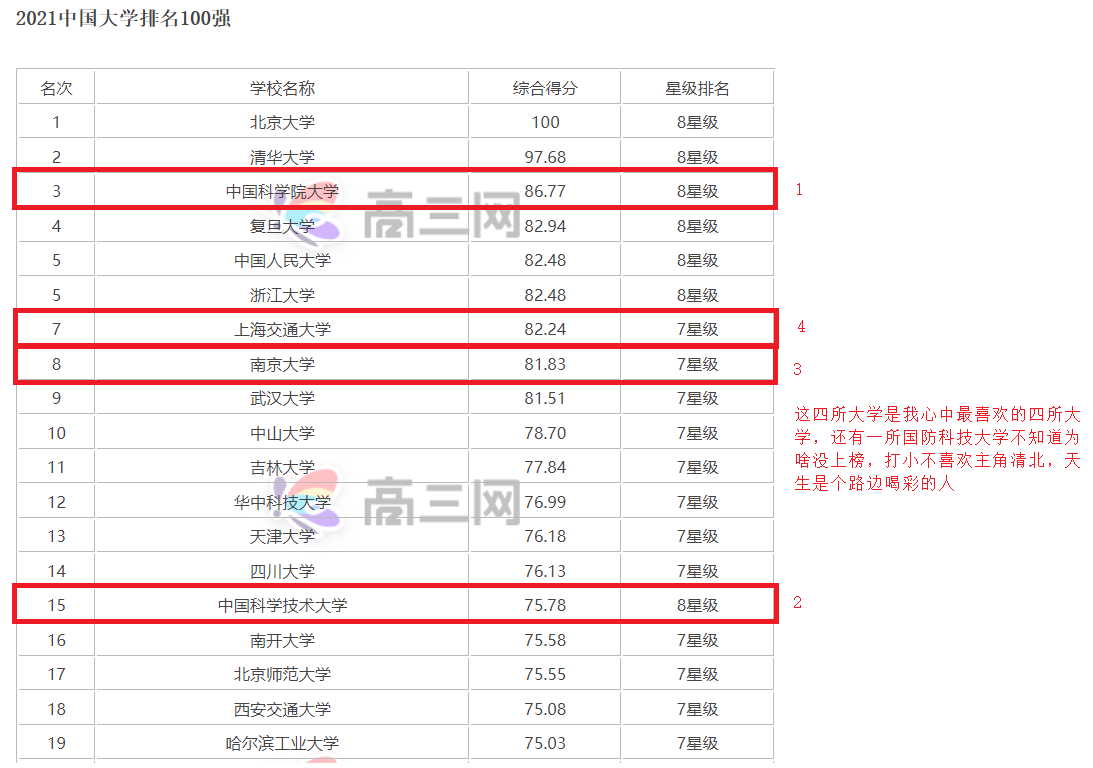
University Ranking

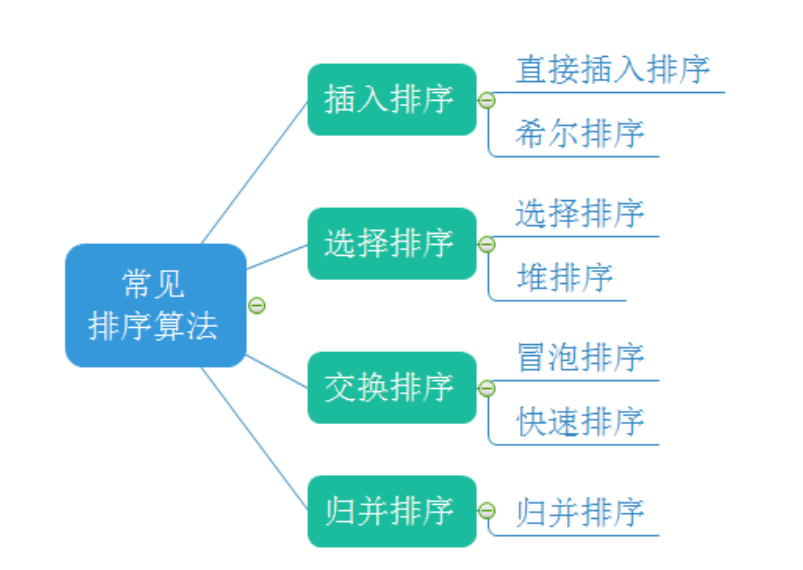
Common sorting algorithms

Implementation of common sorting algorithms

Insert sort

basic thought

Direct insertion sort is a simple insertion sort method. Its basic idea is to insert the records to be sorted into an ordered sequence one by one according to the size of their key values, until all records are inserted, and a new ordered sequence is obtained.

In practice, when we play cards, we use the idea of insertion sorting

But the array is definitely not ordered, so we have to order the array first

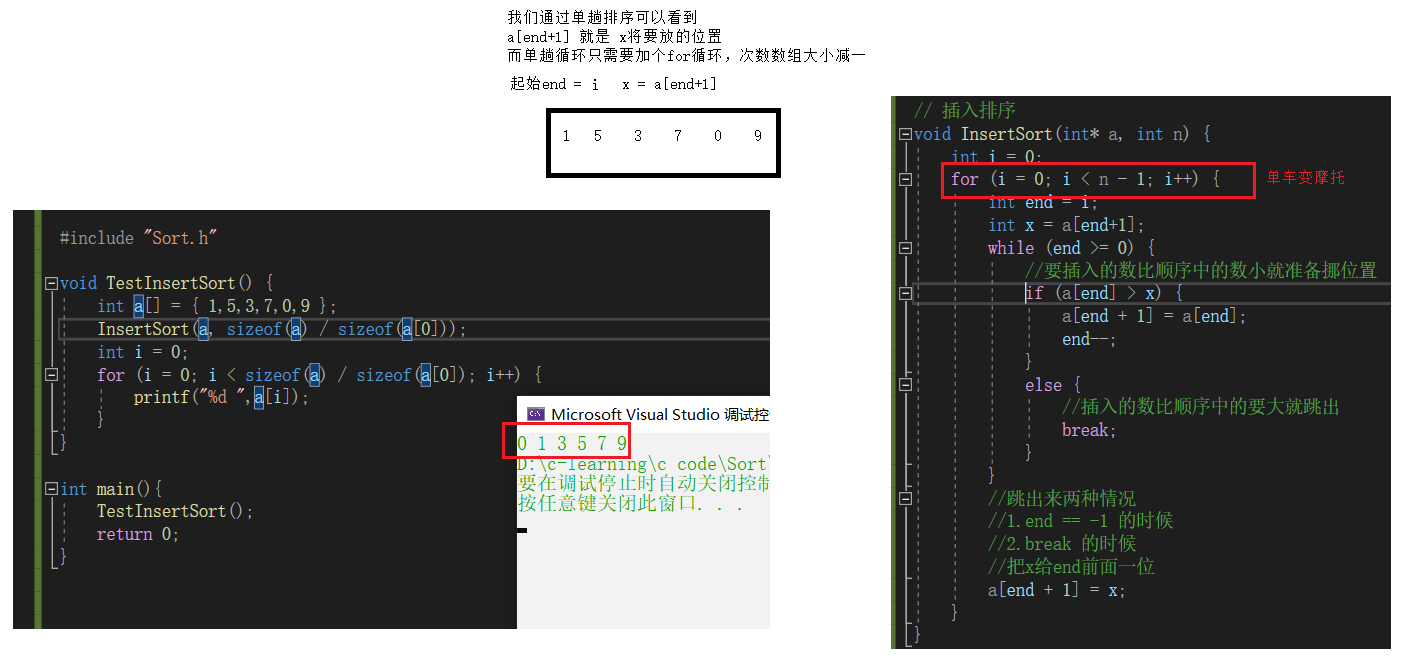
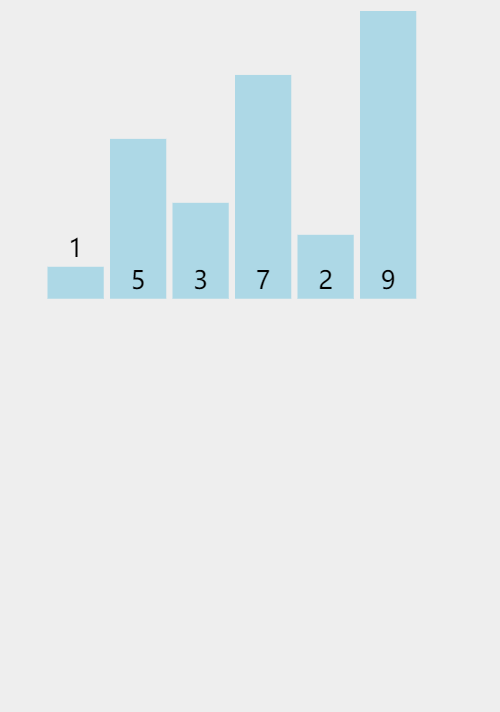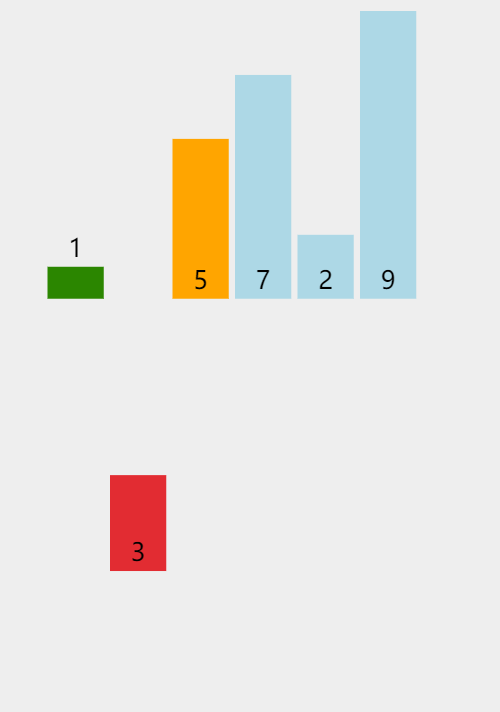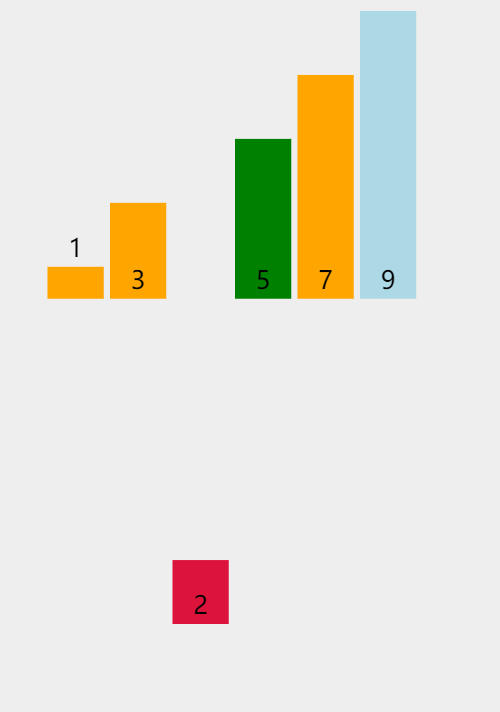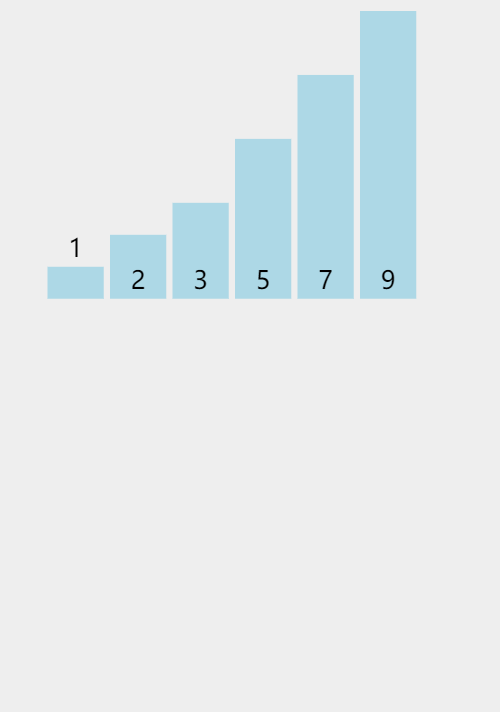
First peel out the print array

// Print array
void PrintArray(int* a, int n) {
	assert(a);
	int i = 0;
	for (i = 0; i < n; i++) {
		printf("%d ", a[i]);
	}
	printf("\n");
}

Insert sort

// Insert sort
void InsertSort(int* a, int n) {
	assert(a);
	int i = 0;
	for (i = 0; i < n - 1; i++)	{
		int end = i;
		int x = a[end+1];
		while (end >= 0) {
			//If the number to be inserted is smaller than the number in the sequence, prepare to move the position
			if (a[end] > x) {
				a[end + 1] = a[end];
				end--;
			}
			else {
				//If the number inserted is larger than that in the sequence, it will jump out
				break;
			}
		}
		//Jump out of two situations
		//1.end == -1
		//2.break
		//Give x to the one in front of end
		a[end + 1] = x;
	}
}

Time complexity of insertion sort: O(N2)

Best: O(N) - sequential (near sequential)

Worst case: O(N2) - reverse order

Space complexity of insert sort: O(1)

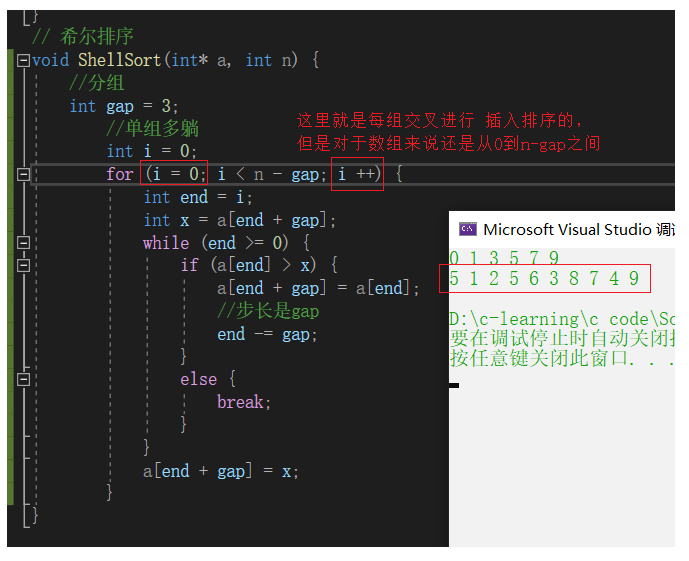
Hill sort (reduced incremental sort) (Hill's force anyway)

Hill sort is optimizing direct insertion sort, and the effect is super obvious. Why optimization? Because we know that direct insertion sort will be very fast when it is close to order. Then I will create such an order to make its time complexity close to O(N). We know that the best time complexity of sorting is O(N), and our approach to O(N) is quite great, Almost close to the ceiling

Hill ranking method is also known as reduced incremental method. The basic idea of hill sorting method is to select an integer first, divide all records in the file to be sorted into groups, divide all records with distance into the same group, and sort the records in each group. Then, take and repeat the above grouping and sorting. When arrival = 1, all records are arranged in a unified group.

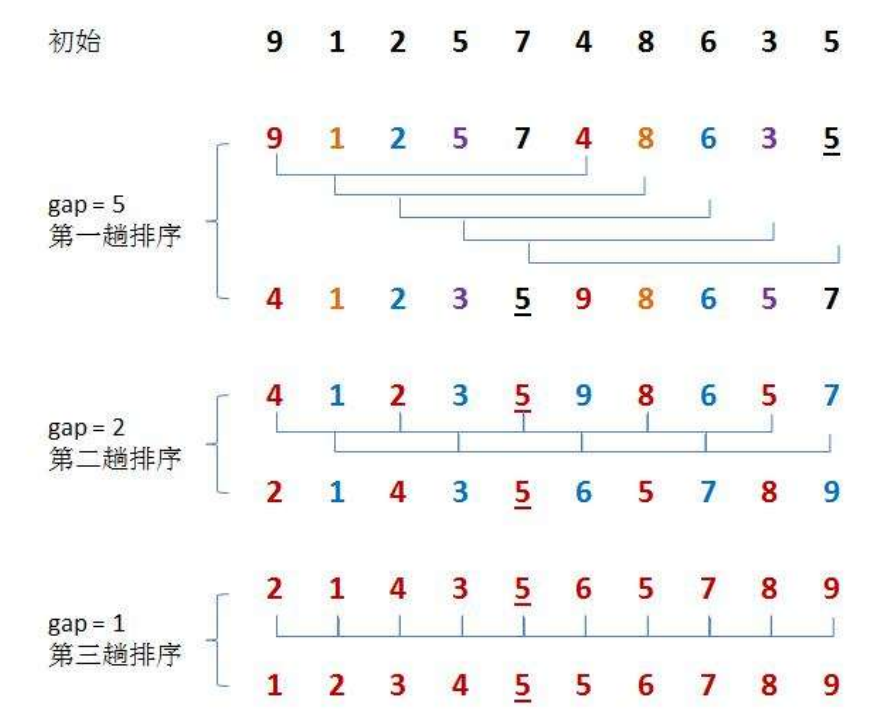
Hill sort step

1. Group pre sorting - the array is close to order

Group by gap, insert and sort the grouping values, and divide them into gap groups

2. The direct insertion sort array is close to order, and the time complexity of direct insertion is O(N)

Single group multi lying

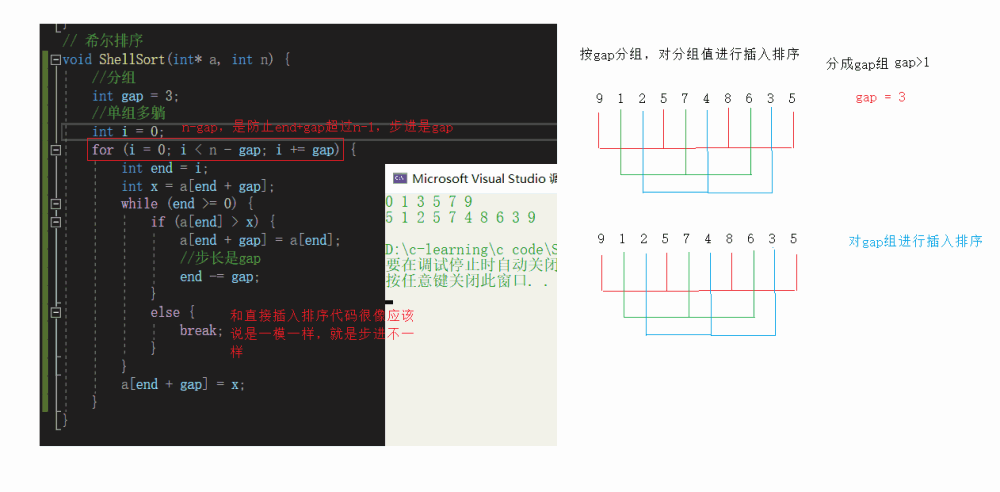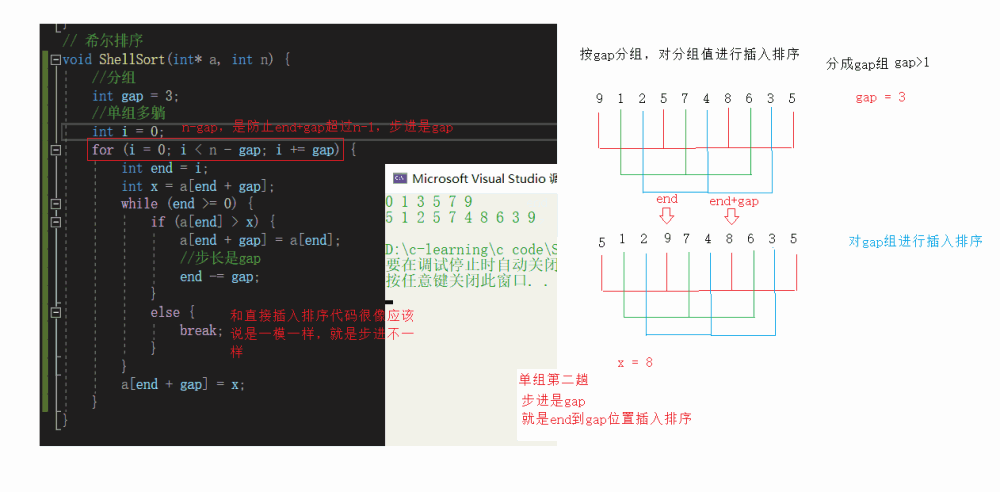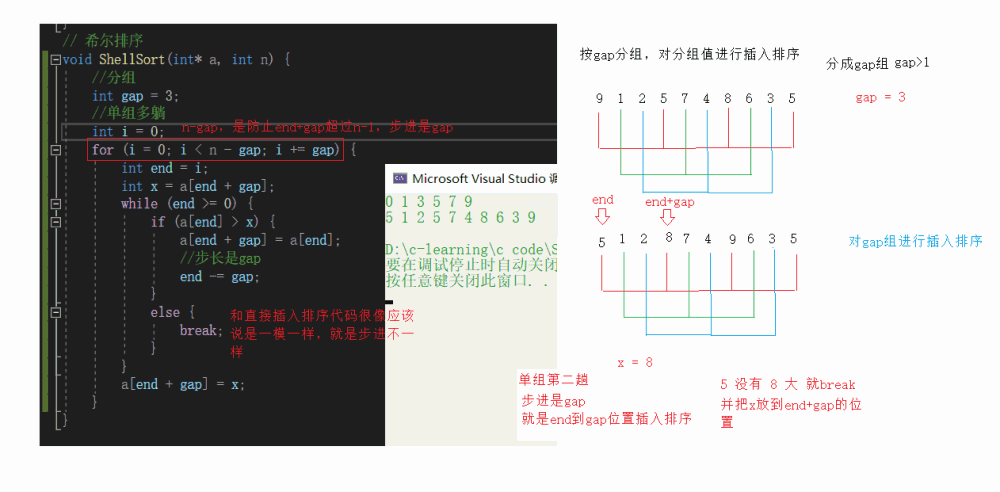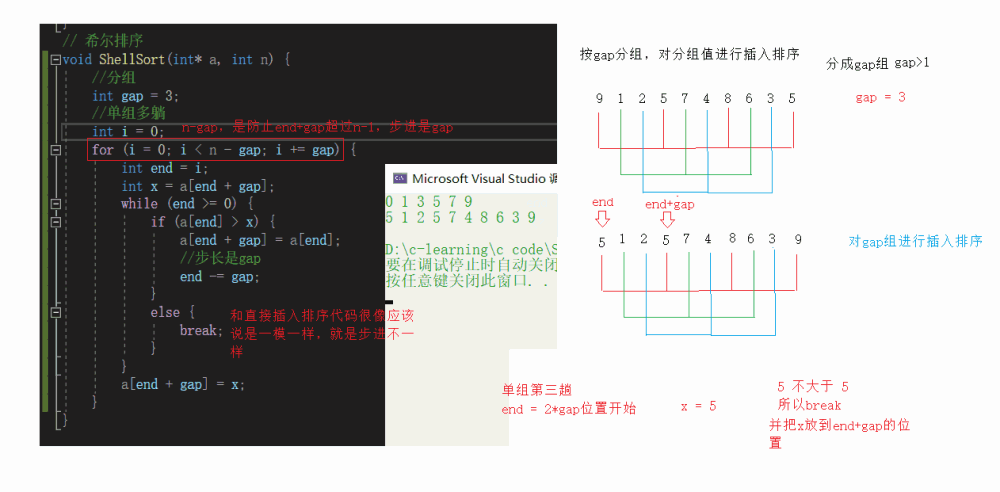
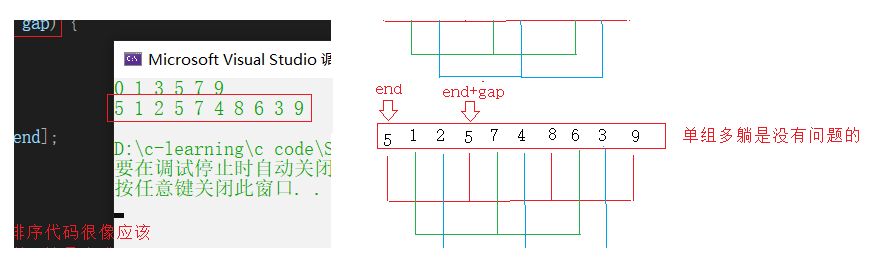
Multi group insertion

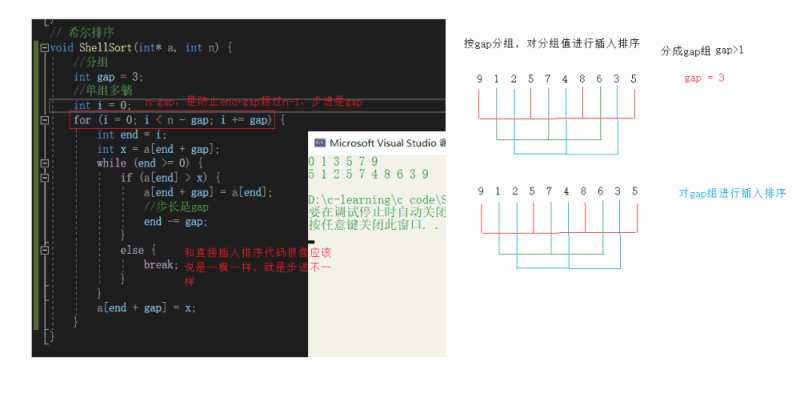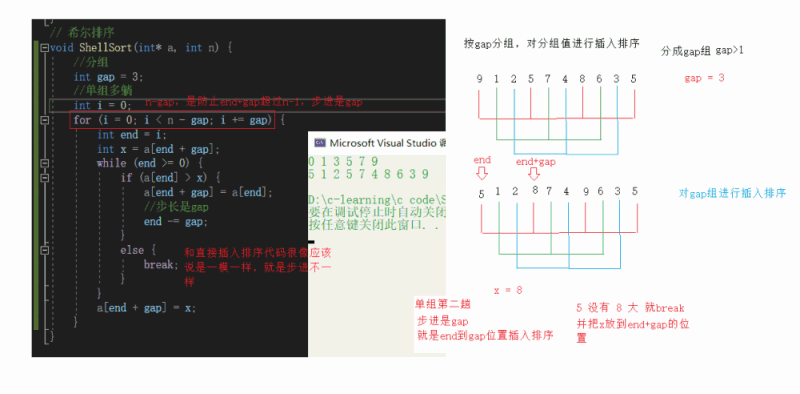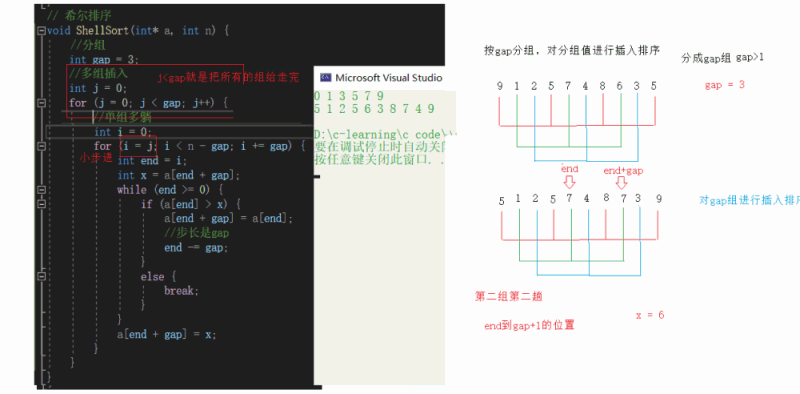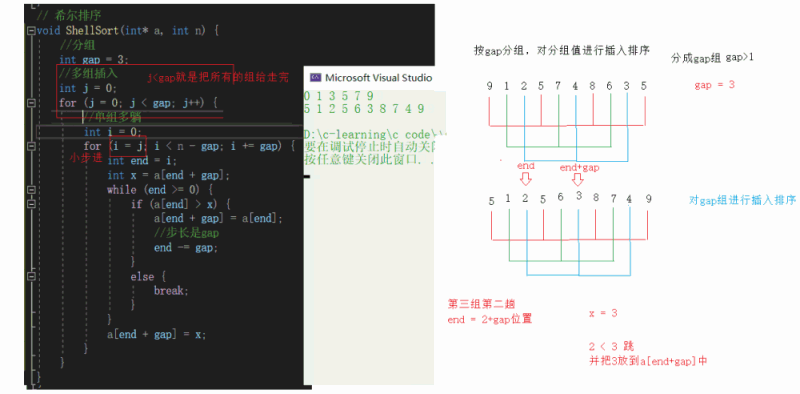
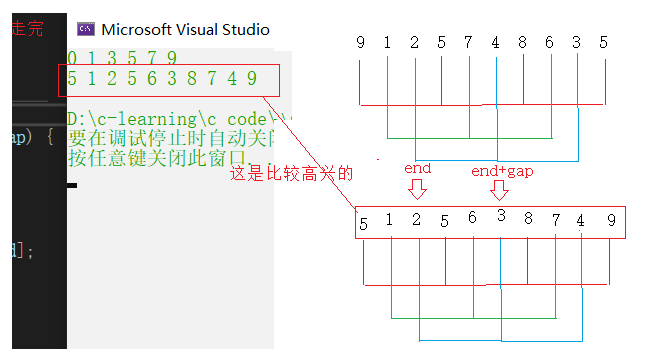
Time complexity O(gap*(1 +... + N/gap))

Best: O(N)

Best: O(N)

Worst case: O(gap*(1 +... + N/gap))

The larger the gap, the faster the pre scheduling, and the less ordered the pre scheduling

The smaller the gap, the slower the pre scheduling, and the closer to order after pre scheduling

Stew in one pot in multiple groups (we can also stew in one pot if it's troublesome to insert in groups)

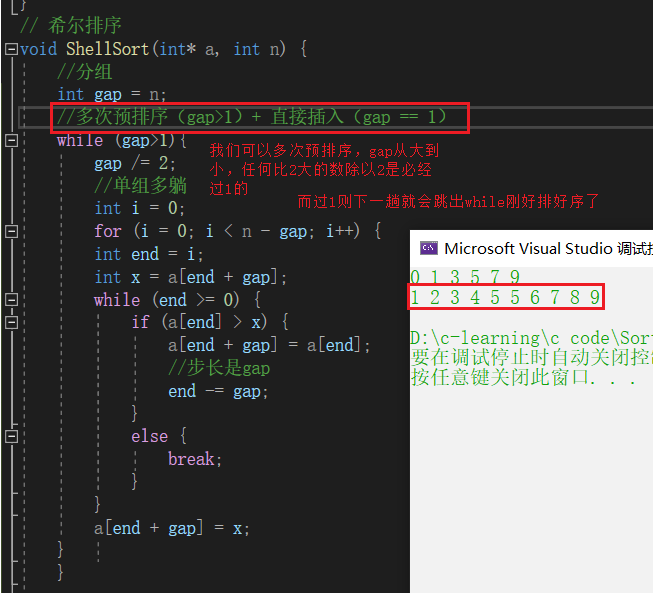
Multiple pre sorting (gap > 1) + direct insertion (gap == 1)

gap/2

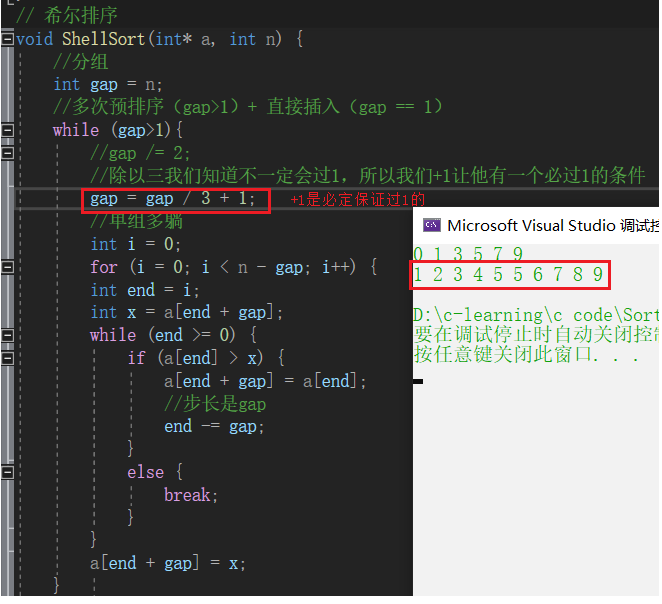
gap/3

Time complexity O(N1.3) just remember. Anyway, remember that hill is very powerful, and Hill sorting is very fast

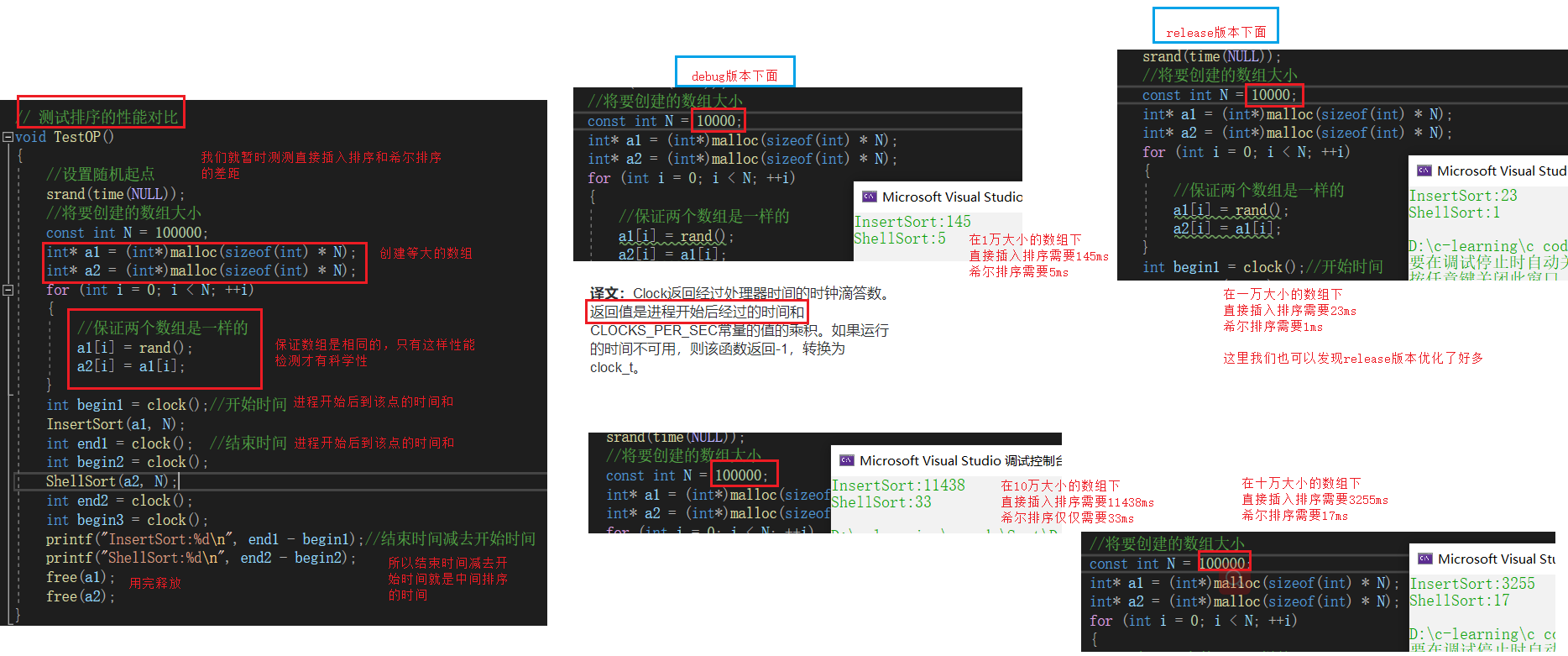
Test the performance of direct insertion sort and Hill sort (let's see what Hill sort is)

code

Sort.h

#pragma once
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <time.h>

// Interface for sorting implementation
// Print array
extern void PrintArray(int* a, int n);
// Insert sort
extern void InsertSort(int* a, int n);
// Shell Sort 
extern void ShellSort(int* a, int n);
// Select sort
extern void SelectSort(int* a, int n);
// Heap sort
extern void AdjustDwon(int* a, int n, int root);
extern void HeapSort(int* a, int n);
// Bubble sorting
extern void BubbleSort(int* a, int n);
// Recursive implementation of quick sort
// Quick sort hoare version
extern int PartSort1(int* a, int left, int right);
// Quick sequencing excavation method
extern int PartSort2(int* a, int left, int right);
// Quick sort before and after pointer method
extern int PartSort3(int* a, int left, int right);
extern void QuickSort(int* a, int left, int right);
// Non recursive implementation of quick sort
extern void QuickSortNonR(int* a, int left, int right);
// Recursive implementation of merge sort
extern void MergeSort(int* a, int n);
// Non recursive implementation of merge sort
extern void MergeSortNonR(int* a, int n);
// Count sort
extern void CountSort(int* a, int n);

Sort.c

#define _CRT_SECURE_NO_WARNINGS 1

#include "Sort.h"

// Print array
void PrintArray(int* a, int n) {
	assert(a);
	int i = 0;
	for (i = 0; i < n; i++) {
		printf("%d ", a[i]);
	}
	printf("\n");
}
// Insert sort
void InsertSort(int* a, int n) {
	assert(a);
	int i = 0;
	for (i = 0; i < n - 1; i++)	{
		int end = i;
		int x = a[end+1];
		while (end >= 0) {
			//If the number to be inserted is smaller than the number in the sequence, prepare to move the position
			if (a[end] > x) {
				a[end + 1] = a[end];
				end--;
			}
			else {
				//If the number inserted is larger than that in the sequence, it will jump out
				break;
			}
		}
		//Jump out of two situations
		//1.end == -1
		//2.break
		//Give x to the one in front of end
		a[end + 1] = x;
	}
}
// Shell Sort 
void ShellSort(int* a, int n) {
	//grouping
	int gap = n;
	//Multiple pre sorting (gap > 1) + direct insertion (gap == 1)
	while (gap>1){
		//gap /= 2;
		//Divided by three, we know that we don't have to pass 1, so we + 1 let him have a condition that he must pass 1
		gap = gap / 3 + 1;
		//Single group multi lying
		int i = 0;
		for (i = 0; i < n - gap; i++) {
		int end = i;
		int x = a[end + gap];
		while (end >= 0) {
			if (a[end] > x) {
				a[end + gap] = a[end];
				//The step size is gap
				end -= gap;
			}
			else {
				break;
			}
		}
		a[end + gap] = x;
	}
	}	
}

test.c

#define _CRT_SECURE_NO_WARNINGS 1

#include "Sort.h"

// Performance comparison of test sorting
void TestOP()
{
	//Set random start point
	srand(time(NULL));
	//The size of the array to be created
	const int N = 100000;
	int* a1 = (int*)malloc(sizeof(int) * N);
	int* a2 = (int*)malloc(sizeof(int) * N);
	for (int i = 0; i < N; ++i)
	{
		//Ensure that the two arrays are the same
		a1[i] = rand();
		a2[i] = a1[i];
	}
	int begin1 = clock();//start time
	InsertSort(a1, N);
	int end1 = clock();  //End time
	int begin2 = clock();
	ShellSort(a2, N);
	int end2 = clock();
	int begin3 = clock();
	printf("InsertSort:%d\n", end1 - begin1);//End time minus start time 
	printf("ShellSort:%d\n", end2 - begin2);
	free(a1);
	free(a2);
}
//Test insert sort
void TestInsertSort() {
	int a[] = { 1,5,3,7,0,9 };
	InsertSort(a, sizeof(a) / sizeof(a[0]));	
	PrintArray(a, sizeof(a) / sizeof(a[0]));
}
//Test Hill sort
void TestShellSort() {
	int a[] = { 9,1,2,5,7,4,8,6,3,5 };
	ShellSort(a, sizeof(a) / sizeof(a[0]));
	PrintArray(a, sizeof(a) / sizeof(a[0]));
}
int main(){
	//TestInsertSort();
	//TestShellSort();
	TestOP();
	return 0;
}