What is an algorithm?

At ordinary times, children who study computer often hear the word algorithm. What is an algorithm?
There is no clear definition of the algorithm. According to my personal understanding, the algorithm is to solve a specific problem and describe the ideas and steps of solving the problem.

In fact, there are many articles on the top ten algorithms on the Internet. The leaders write very well. The leaders have a high level, so the articles are relatively deep. I am a newcomer. This article is also especially suitable for newcomers who have just started learning. Let's start with it.

Top ten sorting algorithms

🎈 Bubble sorting

analysis

Bubble ranking is the most basic exchange ranking, just like the coke we usually drink, from the bottom to the top. The specific implementation method is to move to one side bit by bit according to the size of the number. If you move the small number from the right to the left in the order from small to large.
For example: sort the five numbers in 3.2.5.8.1 from small to large

1. The first step is to start the comparison from the right, move the small number to the left, compare 1 with 8 first, so 1 and 8 exchange positions.

2. In the second step, 1 is compared with 5, or 1 is smaller and 5 is interchanged.

3. Similarly, until all comparisons are made, 1 is the smallest in the first position

4. Then start the comparison again. 8 is bigger than 5, so you don't need to move. Then compare 2 with 5, 5 doesn't need to move, 2 and 3 compare, 2 and 3 exchange positions, 2 and 1 don't need to move, and then compare from right to left. The final result is 1.2.3.5.8

code implementation

function bubbleSort(arr) {
    var len = arr.length;
    for (var i = 0; i < len - 1; i++) {
        for (var j = 0; j < len - 1 - i; j++) {
            if (arr[j] > arr[j+1]) {        // Pairwise comparison of adjacent elements
                var temp = arr[j+1];        // Element exchange
                arr[j+1] = arr[j];
                arr[j] = temp;
            }
        }
    }
    return arr;
}

Examples

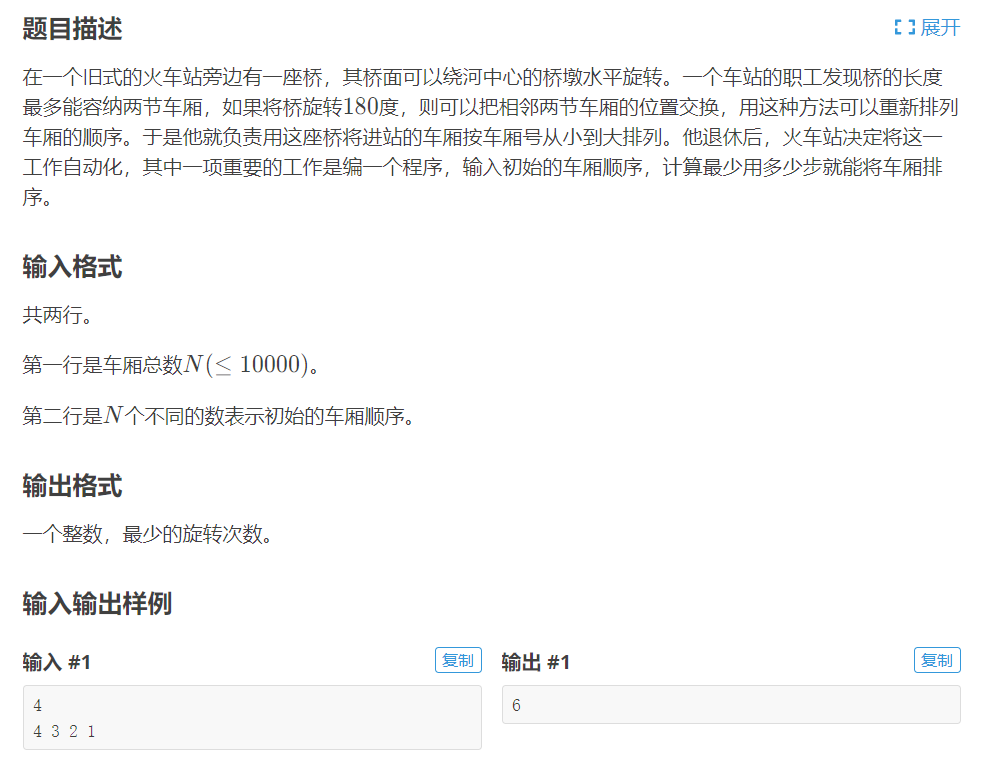
Bubble sorting is used in this topic. If the previous number is larger than the latter, ans will add 1

#include<stdio.h>
int main()
{
	int n;
	scanf("%d",&n);
	int a[n+1],ans;
	ans=0;
	for(int i=1;i<=n;i++)
		scanf("%d",&a[i]);
	for(int i=1;i<=n;i++)
		for(int j=1;j<=i;j++)
			if(a[i]<a[j])
				ans++;
	printf("%d",ans);
}

🎈 Select sort

analysis

As the name suggests, select a minimum (large) from all elements and place it at the beginning of the sequence, and then select a minimum (large) from the remaining queue and place it at the second position.
For example: sort the five numbers in 3.2.5.8.1 from small to large
1. Step 1: first select the smallest number from all queues. The smallest number is 1, and then put it at the top of the sequence

2. Step 2: find the smallest of the remaining four numbers and put it in the second position. The smallest is 2

3. Step 3: similarly, sort it down in order, and finally

code implementation

function selectionSort(arr) {
    var len = arr.length;
    var minIndex, temp;
    for (var i = 0; i < len - 1; i++) {
        minIndex = i;
        for (var j = i + 1; j < len; j++) {
            if (arr[j] < arr[minIndex]) {     // Find the smallest number
                minIndex = j;                 // Save the index of the smallest number
            }
        }
        temp = arr[i];
        arr[i] = arr[minIndex];
        arr[minIndex] = temp;
    }
    return arr;

Examples

I feel that this question is "tailor-made" for selection and sorting. The first number is the largest, the second number is the smallest, and the third number is the largest from the remaining numbers.

#include<iostream>
using namespace std;
int main(){
	int n=0;
	long int a[1000]={0};
	cin>>n;
	for(int i=0; i<n; i++) cin>>a[i];
	for(int i=0; i<n-1; i++) {
		int min_index = i;
		for(int j=i; j<n; j++) if(a[j] > a[min_index]) min_index = j;//Find the position of the smallest number i
		swap(a[i],a[min_index]);//Place the smallest number i in position i; If it happens, you don't have to exchange
		i++;
		for(int j=i; j<n; j++) if(a[j] < a[min_index]) min_index = j;//Find the position of the smallest number i
		swap(a[i],a[min_index]);//Place the smallest number i in position i; If it happens, you don't have to exchange
}
for(int i=0; i<n; i++) cout<<a[i]<<endl;
}

🎈 Insert sort

analysis

The idea of insertion sort is divided into ordered sequence and unordered sequence. The numbers in unordered sequence are inserted into ordered sequence until all numbers are inserted.
For example: sort the five numbers in 3.2.5.8.1 from small to large
1. Step 1: 3 is an ordered sequence, 2.5.8.1 is an unordered sequence,

2. Take out the first number of the unordered sequence and insert it into the ordered sequence

3. Then insert 5 of the unordered sequence into the ordered sequence

4. Similarly

5. The final result is

code implementation

function insertionSort(arr) {
    var len = arr.length;
    var preIndex, current;
    for (var i = 1; i < len; i++) {
        preIndex = i - 1;
        current = arr[i];
        while (preIndex >= 0 && arr[preIndex] > current) {
            arr[preIndex + 1] = arr[preIndex];
            preIndex--;
        }
        arr[preIndex + 1] = current;
    }
    return arr;
}

Examples

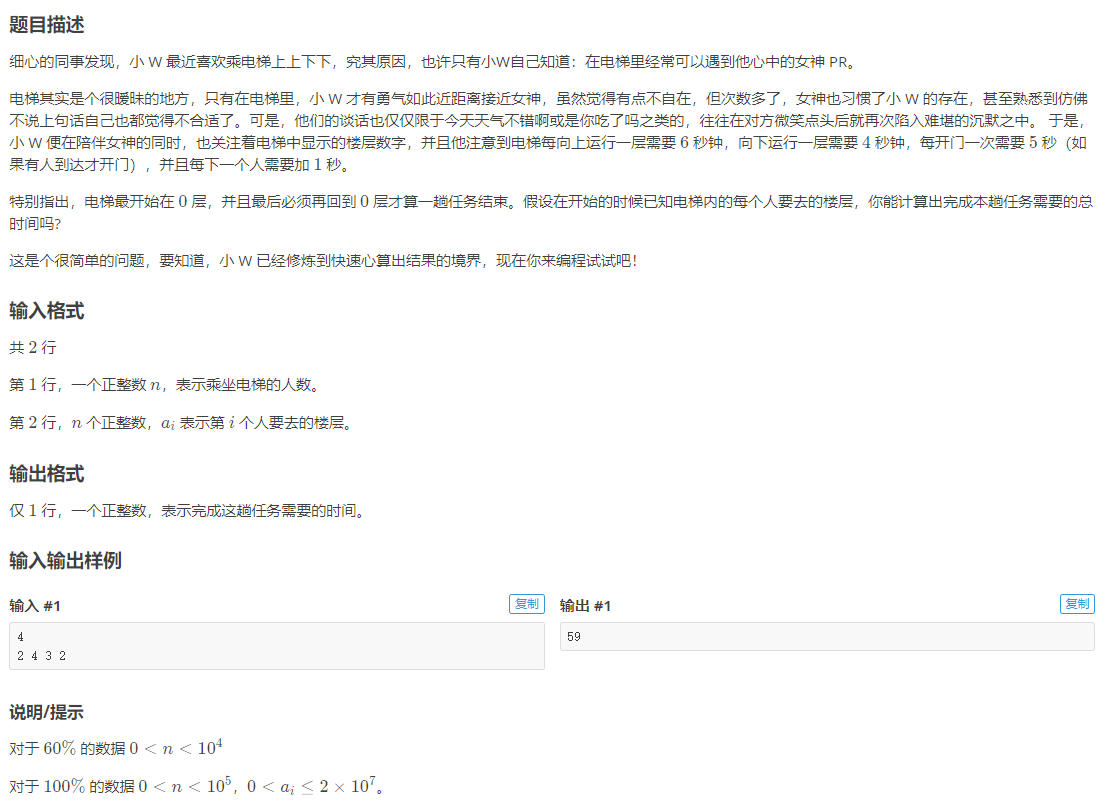
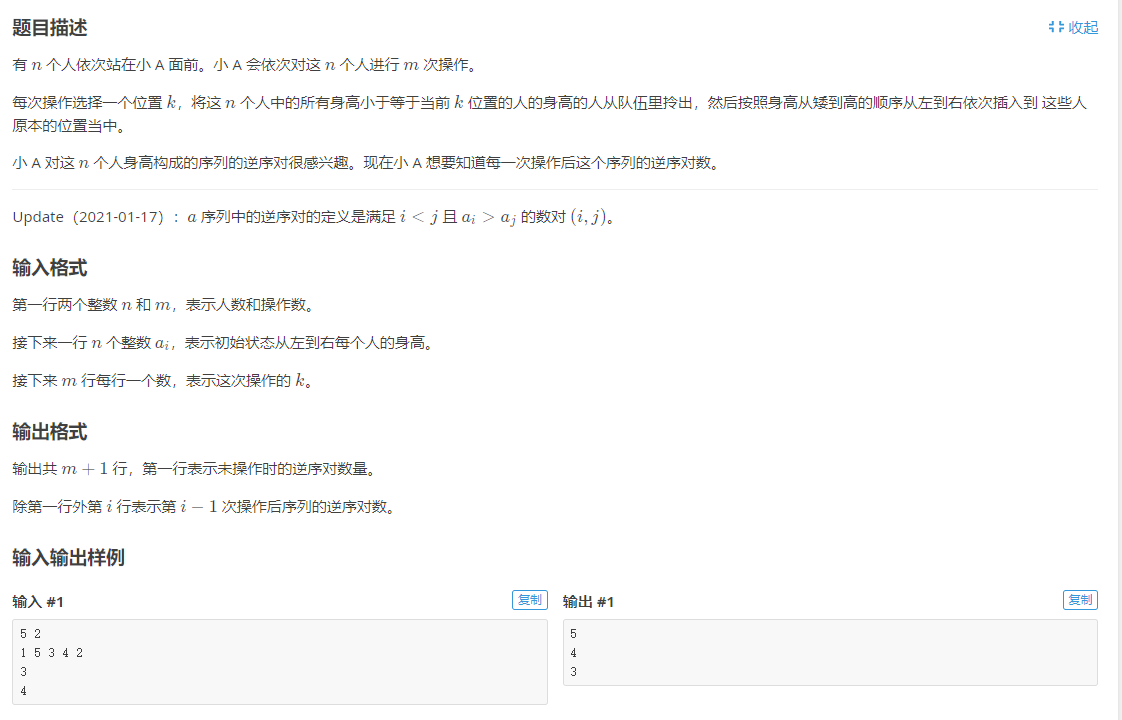
Title Description
After the end of the final examination of Tsinghua affiliated primary school, the scores of 30 students will be input in the order of student number by mathematics, Chinese and English. The head teacher wants to know the highest and lowest scores of the three courses, as well as the numbers of the two students who have obtained the highest and lowest scores. (the input data shall ensure that there is no same division, and the number shall be from 1 to 30)
Enter description
In the first line, enter the math scores of 30 students numbered 1-30, separated by spaces; The second line is the Chinese score, and the third line is the English score
Output description
Output four numbers, which are the highest total score, the lowest total score, the number of students who get the highest score and the number of students who get the lowest score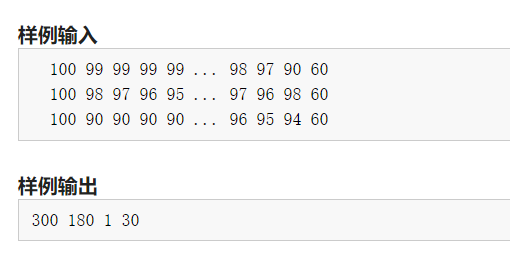

#include <iostream>

#include <stdlib.h>
using namespace std;
int main() {
int*math = new int[3];
int*chinese = new int[3];
int*english = new int[3];
for (int n = 0; n < 3; n++) {
cin >> math[n];
}
for (int n = 0; n < 3; n++) {
cin >> chinese[n];
}
for (int n = 0; n < 3; n++) {
cin >> english[n];
}
int*sum= new int[3];
int*order = new int[3];
for (int n = 0; n < 3; n++) {
sum[n] = math[n] + chinese[n] + english[n];
}  
for (int n = 0; n <= 2; n++) {
order[n] = sum[n];
}
for (int n = 1; n <=2; n++){
int now = sum[n], space = 0;
while (now > sum[space])
space++;
for (int i = n; i > space; i--)
sum[i] = sum[i - 1];
sum[space] = now;
}
int max, min;
for (int n = 0; n <= 2; n++) {
if (order[2] == sum[n])
max = n;
if (order[0] == sum[n])
min = n;
}
cout << sum[2] << endl;
cout << sum[0] << endl;
cout << max<<endl;
cout << min<<endl;
system("pause");  
return 0;
}

🎈 Shell Sort

analysis

The main idea of Hill sort is to group the data, and then insert sort each group of data. After each group of data is in order, all groups are sorted by insert sort for the last time. It can be said that it is an upgraded version of insertion sorting, which can speed up the sorting by reducing the number of data exchanges.
For example: sort the six numbers in 3.2.5.8.1.6 from small to large
1. Step 1: grouping is based on two groups, six numbers are divided into three groups, the first and fourth groups, the second and fifth groups, and the third and sixth groups.
2. Step 2: compared with 3 and 8, compared with 2 and 1, compared with 5 and 6, the small row is in front of the large row

3. Step 3: then divide into 3 / 2 = 1 groups and directly insert and sort all data

code implementation

function shellSort(arr) {
    var len = arr.length;
    for (var gap = Math.floor(len / 2); gap > 0; gap = Math.floor(gap / 2)) {
        // Note: This is different from the dynamic diagram. The dynamic diagram is executed in groups, and the actual operation is that multiple groups are executed alternately
        for (var i = gap; i < len; i++) {
            var j = i;
            var current = arr[i];
            while (j - gap >= 0 && current < arr[j - gap]) {
                 arr[j] = arr[j - gap];
                 j = j - gap;
            }
            arr[j] = current;
        }
    }
    return arr;
}

Examples

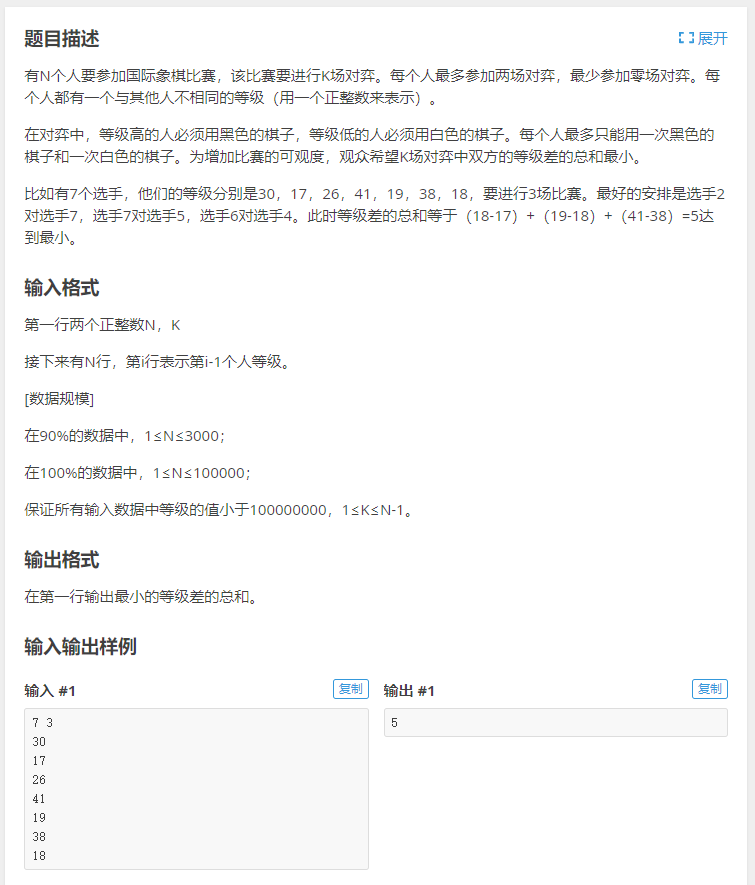
#include<iostream> 
#include<cstdio> 
#include<algorithm> 
using namespace std; 
int main()
{
    int n,k,i,a[100001],b[100001],ans=0;
    scanf("%d%d",&n,&k);
    for(i=1;i<=n;i++)
    scanf("%d",&a[i]);
    sort(a+1,a+n+1);//Sort sort from small to large 
    for(i=1;i<=n-1;i++)
    b[i]=a[i+1]-a[i];//Calculate the difference of players at all levels 
    sort(b+1,b+n);//Sort sort from small to large 
    for(i=1;i<=k;i++)
    ans+=b[i];//Find the sum of the first K grade differences 
    printf("%d",ans);//output 
    return 0;
}

🎈 Merge sort

analysis

The main idea of merging and sorting is to divide the elements of the whole sequence into half groups layer by layer, then compare and sort from the smallest group, merge into a large group, and carry out layer by layer. Finally, all elements are orderly.
For example: sort the six numbers in 3.2.5.8.1.6 from small to large
1. Step 1: first, divide into groups by half layer by layer. Two groups are divided into three groups.

2. Step 2: then sort each group

3. Step 3: then merge layer by layer, from small to large.

4. Step 4: sort and merge

A dynamic diagram is inserted here for your understanding

code implementation

function mergeSort(arr) {
    var len = arr.length;
    if (len < 2) {
        return arr;
    }
    var middle = Math.floor(len / 2),
        left = arr.slice(0, middle),
        right = arr.slice(middle);
    return merge(mergeSort(left), mergeSort(right));
}
 
function merge(left, right) {
    var result = [];
 
    while (left.length>0 && right.length>0) {
        if (left[0] <= right[0]) {
            result.push(left.shift());
        } else {
            result.push(right.shift());
        }
    }
 
    while (left.length)
        result.push(left.shift());
 
    while (right.length)
        result.push(right.shift());
 
    return result;
}

Examples

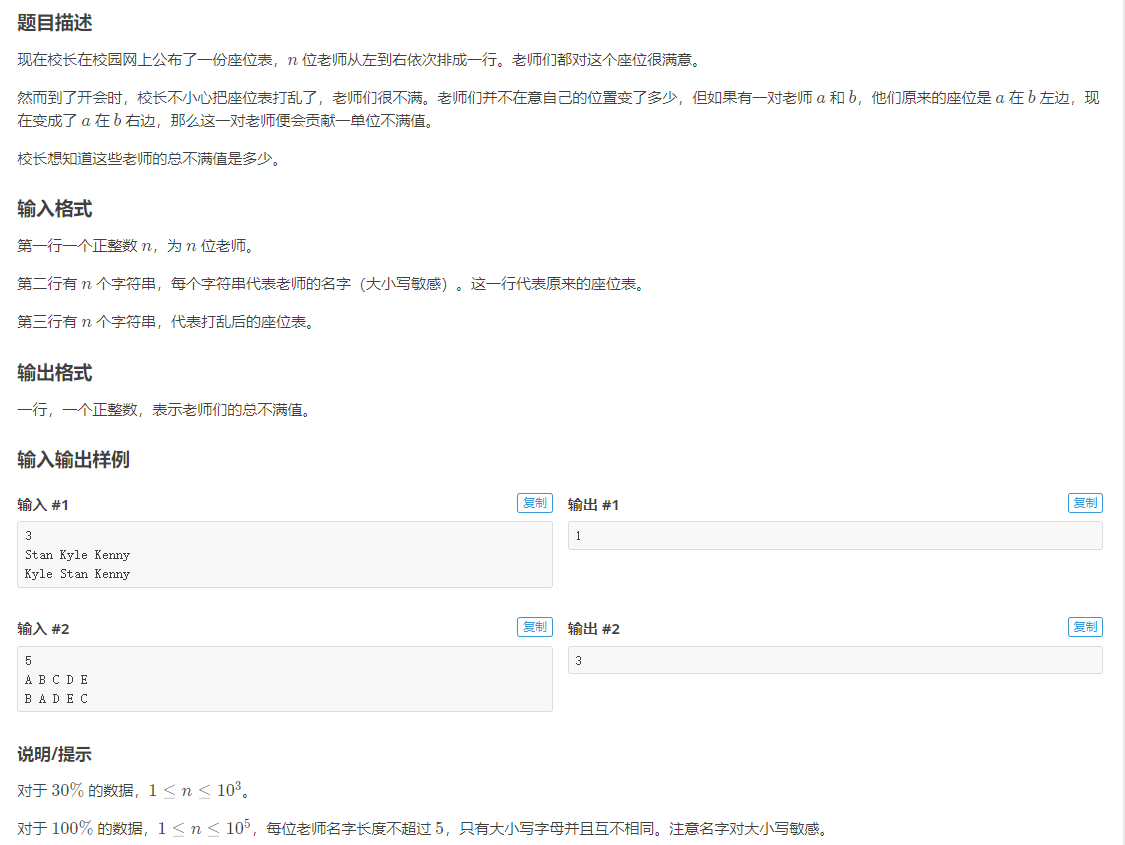
#include<iostream>
#include<cstdio>
#include<cmath>
#include<map>
using namespace std;
string s;
map<string,int>nmsl;
int n;
long long ans=0;
int c[1000001],d[1000001];
void qsort(int a,int b)
{	
    if(a==b)return;
	int mid=(a+b)>>1;
	int i=a,j=mid+1,k=a;
    qsort(a,mid),qsort(mid+1,b);
    while(i<=mid&&j<=b)
	if(c[i]<=c[j])
	  {
	  	d[k++]=c[i++];
	  }
	else 
	  {
	  	d[k++]=c[j++];
	  	ans+=mid-i+1;
	  }
	while(i<=mid)
	  	d[k++]=c[i++];
	while(j<=b)
	    d[k++]=c[j++];
	for(int l=a;l<=b;l++)
	    c[l]=d[l];
}
int main()
{
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
	   {
	   	cin>>s;
	   	nmsl[s]=i;
	   }
	int j=0;
	for(int i=1;i<=n;i++)
	{
		 cin>>s;
		 c[++j]=nmsl[s];
	}
	qsort(1,n);
	printf("%lld",ans);
	return 0;
}

🎈 Quick sort

analysis

Quick sort is to take a number from the sequence as the benchmark number. The partitioning process is to put all numbers larger than this number on its right, and all numbers less than or equal to it on its left, and then repeat the second step for the left and right intervals until there is only one number in each interval
For example: sort the six numbers in 3.2.5.8.1.6 from small to large
1. Step 1: take 3 as the benchmark, move the larger one to the right and the smaller one to the left

2. Step 2: then sort the left side of 3 based on 2

3. Step 3: sort the right side of 3 based on 8

code implementation

function quickSort(arr, left, right) {
    var len = arr.length,
        partitionIndex,
        left = typeof left != 'number' ? 0 : left,
        right = typeof right != 'number' ? len - 1 : right;
 
    if (left < right) {
        partitionIndex = partition(arr, left, right);
        quickSort(arr, left, partitionIndex-1);
        quickSort(arr, partitionIndex+1, right);
    }
    return arr;
}
 
function partition(arr, left ,right) {     // Partition operation
    var pivot = left,                      // Set reference value (pivot)
        index = pivot + 1;
    for (var i = index; i <= right; i++) {
        if (arr[i] < arr[pivot]) {
            swap(arr, i, index);
            index++;
        }       
    }
    swap(arr, pivot, index - 1);
    return index-1;
}
 
function swap(arr, i, j) {
    var temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}

Examples

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<bits/stdc++.h>
int n;
int ans=0;
int i,j,k;
int a[100010];
using namespace std;
int main(){
    cin>>n;
    j=0;
    for(i=1;i<=n;i++)
    cin>>a[i];
    sort(a,a+n+1);//Sort from small to large
    ans=n+a[n]*10;//The time needed by everyone and the time for getting up and down the elevator
    for(i=1;i<=n;i++){
        if(a[i]!=a[i-1]){//From the beginning of the loop, the default initial value of the array is 0 to avoid missing all on the same floor
            ans=ans+5;//The elevator needs a switch
        }
    }
    cout<<ans;
    return 0;
}

🎈 Count sort

analysis

Counting sorting is a non comparison based sorting algorithm. Its core is to convert the input data values into keys and store them in the additional array space to achieve the sorting effect
For example: sort the six numbers in 3.2.5.8.1.6 from small to large
1. Step 1: first determine the maximum number and minimum number of all elements to be sorted

2. Step 2: then open up a new array space. The minimum value is 1 and the maximum value is 8

3. Then arrange the elements in the new array space from small to large

Insert a dynamic diagram for everyone to understand

code implementation

function countingSort(arr, maxValue) {
    var bucket = new Array(maxValue + 1),
        sortedIndex = 0;
        arrLen = arr.length,
        bucketLen = maxValue + 1;
 
    for (var i = 0; i < arrLen; i++) {
        if (!bucket[arr[i]]) {
            bucket[arr[i]] = 0;
        }
        bucket[arr[i]]++;
    }
 
    for (var j = 0; j < bucketLen; j++) {
        while(bucket[j] > 0) {
            arr[sortedIndex++] = j;
            bucket[j]--;
        }
    }
 
    return arr;
}

Examples

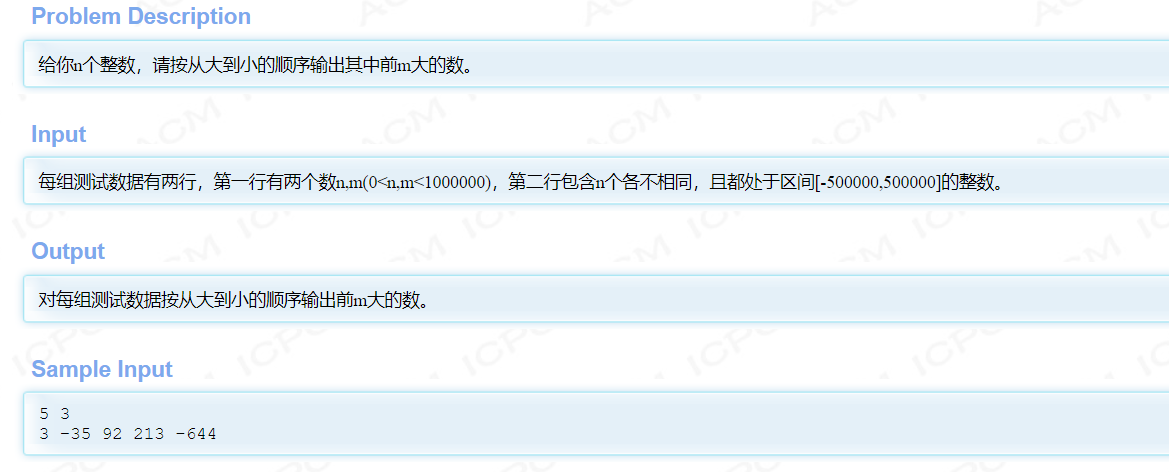
#include <iostream>
#include <cstdio>
#include <cstring>
#include <sstream>
#include <string>
#include <algorithm>
#include <list>
#include <map>
#include <vector>
#include <queue>
#include <stack>
#include <cmath>
#include <cstdlib>
using namespace std;
int  const maxk = 1000005,maxn = 1000005;
//Interface: a[i] original array. ranked[i] ordered array, number of maxn arrays, range of maxk numbers
//Call jishusport (n, maxk)// N represents the size of the array
int a[maxn],ranked[maxn],cnt[maxk];//cnt[i] number less than or equal to I
 
void jishusort(int n,int k)//The size of the n array and the range of numbers in the k array
{
    for(int i = 0; i < n; i ++)
    {
         cnt[a[i] + 500000] ++;
    }
    for(int i = 1; i < k; i ++)
    {
        cnt[i] += cnt[i - 1];
    }
    for(int i = n -1 ; i >= 0; i --)
    {
        ranked[--cnt[a[i]+ 500000]] = a[i];
    }
}
 
int main()
{
	//freopen("in.txt","r",stdin);
	int n,m;
	while(scanf("%d%d",&n,&m)!= EOF){
            memset(cnt,0,sizeof(cnt));
	for(int i = 0; i < n; i ++)
    {
        scanf("%d",&a[i]);
 
    }
    jishusort(n,maxk);
    for(int i = n - 1; i > n  - m; i --)
    {
        printf("%d ",ranked[i]);
    }
    printf("%d\n",ranked[n  - m]);
 
 
	}
 
	return 0;
}
//Forgot multiple sets of data
//Forgot to empty

🎈 Cardinality sort

analysis

Cardinality sorting is to unify each element of the sequence to be sorted into elements with the same bit length. If the bit length is short, the length is consistent by supplementing 0, and then carry out stable counting sorting from the lowest or highest bit, and finally form an ordered sequence. Cardinal sorting is mainly used to sort integers. Because integers can also represent strings or floating-point numbers in a specific format, other data types that can be expressed by integers can also be sorted by cardinality.
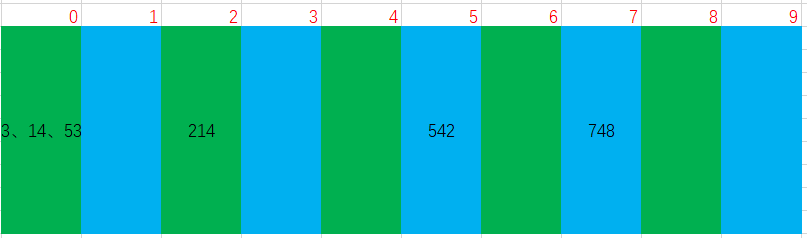
For example, the array {53, 3, 542, 748, 14, 214} is sorted in ascending order using cardinality.
Round 1 sort [sort by bit]:
Note: prepare 10 arrays (10 buckets) in advance, and 0-9 respectively correspond to 0-9 digits
(1) Put each number into the corresponding array according to the bit size
(2) Then take out from 0-9 arrays / buckets in the order of adding elements
After the first round of sorting: 542 53 3 14 214 748

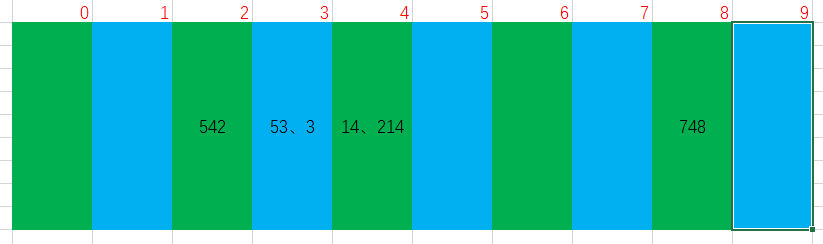
Round 2 [sort by tens]
(1) Put each number into the corresponding array according to the size of ten bits
(2) Then take out from 0-9 arrays / buckets in the order of adding elements
After the second round of sorting: 3 14 214 542 748 53

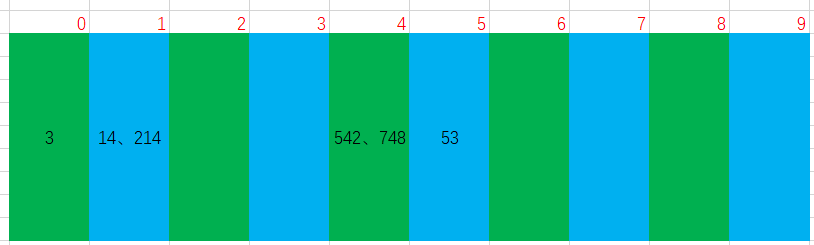
Round 3 [sort by hundredth]
(1) Put each number into the corresponding array according to the size of hundreds
(2) Then take out from 0-9 arrays / buckets in the order of adding elements
After the third round of sorting: 3 14 53 214 542 748 (the order we want is obtained)

code implementation

var counter = [];
function radixSort(arr, maxDigit) {
    var mod = 10;
    var dev = 1;
    for (var i = 0; i < maxDigit; i++, dev *= 10, mod *= 10) {
        for(var j = 0; j < arr.length; j++) {
            var bucket = parseInt((arr[j] % mod) / dev);
            if(counter[bucket]==null) {
                counter[bucket] = [];
            }
            counter[bucket].push(arr[j]);
        }
        var pos = 0;
        for(var j = 0; j < counter.length; j++) {
            var value = null;
            if(counter[j]!=null) {
                while ((value = counter[j].shift()) != null) {
                      arr[pos++] = value;
                }
          }
        }
    }
    return arr;
}

Examples

#include <cstdio>
#include <algorithm>
#define int long long

struct node {
	int id, v;
	inline bool operator < (const node x) const {return v < x.v;}
} b[300005];
inline bool operator < (const int x, const node y) {return x < y.v;}
int a[300005], c[300005], s[300005], n, N;
inline void update(const int x) {
	for (int i(x); i <= n; i += (i & ~i + 1)) ++ c[i];
}
inline int query(const int x) {
	int sum(0);
	for (int i(x); i; i -= (i & ~i + 1)) sum += c[i];
	return sum;
}

signed main() {
	int m, last(0);
	scanf("%lld%lld", &n, &m);
	for (int i(1); i <= n; ++ i) scanf("%lld", &b[i].v), b[i].id = i;
	std::sort(b + 1, b + n + 1);
	a[b[1].id] = 1;
	for (int i(2); i <= n; ++ i)
	a[b[i].id] = (b[i].v != b[i - 1].v) + a[b[i - 1].id];
	for (int i(n); i >= 1; -- i)
		s[a[i]] += query(a[i]), update(a[i]);
	N = a[b[n].id];
	for (int i(2); i <= N; ++ i) s[i] += s[i - 1];
	printf("%lld\n", s[N]);
	a[0] = -0x3fffffff;
	while (m --) {
		int k;
		scanf("%lld", &k);
		if (a[k] < a[last]) k = last;
		last = k;
		printf("%lld\n", s[N] - s[a[k]]);
	}
	return 0;
}

🎈 Heap sort

analysis

Heap sorting is a selective sorting algorithm that uses the concept of binary heap to sort. It is divided into two types:
Ascending sort: sort using the largest heap
Descending sort: sort using the smallest heap
For example: add a dynamic diagram to make it clearer for everyone

code implementation

var len;    // Because multiple functions declared need data length, set len as a global variable
 
function buildMaxHeap(arr) {   // Build large top reactor
    len = arr.length;
    for (var i = Math.floor(len/2); i >= 0; i--) {
        heapify(arr, i);
    }
}
 
function heapify(arr, i) {     // Heap adjustment
    var left = 2 * i + 1,
        right = 2 * i + 2,
        largest = i;
 
    if (left < len && arr[left] > arr[largest]) {
        largest = left;
    }
 
    if (right < len && arr[right] > arr[largest]) {
        largest = right;
    }
 
    if (largest != i) {
        swap(arr, i, largest);
        heapify(arr, largest);
    }
}
 
function swap(arr, i, j) {
    var temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}
 
function heapSort(arr) {
    buildMaxHeap(arr);
 
    for (var i = arr.length - 1; i > 0; i--) {
        swap(arr, 0, i);
        len--;
        heapify(arr, 0);
    }
    return arr;
}

Examples

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<queue>
using namespace std;
typedef long long ll;
priority_queue<ll,vector<ll>,greater<ll> > a;//The priority queue is called directly here
#define in(t) freopen("t.in","r",stdin)
#define out(t) freopen("t.out","w",stdout)
#define m(a) memset(a,0,sizeof(a))
int main(){
    long long ans=0,n,t;//ans, be careful to turn on long long, or it will explode
    scanf("%lld",&n);
    for(int i=1;i<=n;i++){
        scanf("%lld",&t);
        a.push(t);
    }
    for(int i=1;i<=n-1;i++){
        int c,d;
        c=a.top();
        a.pop();
        d=a.top();
        a.pop();//Take the minimum two numbers each time
        ans+=c+d;//Add energy
        a.push(c+d);
}//Like the merged fruit, you can refer to the problem solution of the merged fruit for details
    printf("%lld",ans);

    return 0;

}

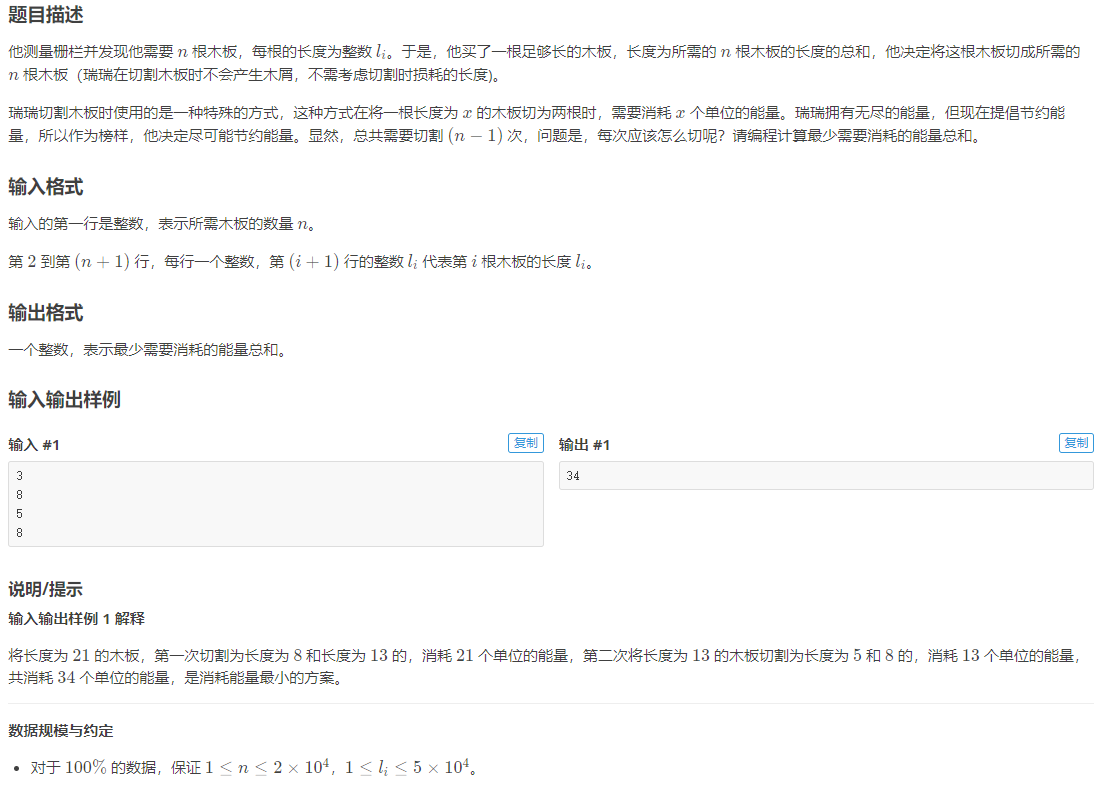
🎈 Bucket sorting

analysis

Bucket sorting is an upgraded version of counting sorting algorithm, which divides the data into a limited number of buckets, and then sorts each bucket separately
give an example:

code implementation

function bucketSort(arr, bucketSize) {
    if (arr.length === 0) {
      return arr;
    }
 
    var i;
    var minValue = arr[0];
    var maxValue = arr[0];
    for (i = 1; i < arr.length; i++) {
      if (arr[i] < minValue) {
          minValue = arr[i];                // Minimum value of input data
      } else if (arr[i] > maxValue) {
          maxValue = arr[i];                // Maximum value of input data
      }
    }
 
    // Initialization of bucket
    var DEFAULT_BUCKET_SIZE = 5;            // Set the default number of buckets to 5
    bucketSize = bucketSize || DEFAULT_BUCKET_SIZE;
    var bucketCount = Math.floor((maxValue - minValue) / bucketSize) + 1;  
    var buckets = new Array(bucketCount);
    for (i = 0; i < buckets.length; i++) {
        buckets[i] = [];
    }
 
    // The mapping function is used to allocate the data to each bucket
    for (i = 0; i < arr.length; i++) {
        buckets[Math.floor((arr[i] - minValue) / bucketSize)].push(arr[i]);
    }
 
    arr.length = 0;
    for (i = 0; i < buckets.length; i++) {
        insertionSort(buckets[i]);                      // Sort each bucket. Insert sort is used here
        for (var j = 0; j < buckets[i].length; j++) {
            arr.push(buckets[i][j]);                     
        }
    }
 
    return arr;
}

Examples

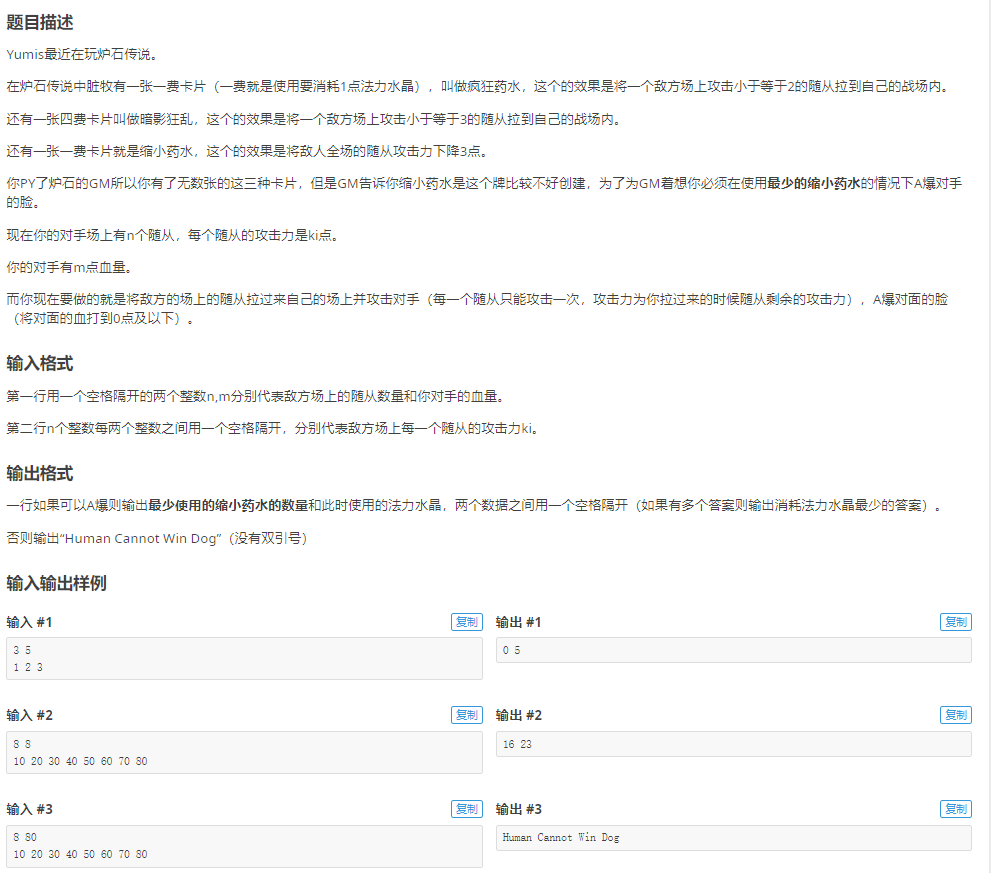
#include <bits/stdc++.h>
const int MAXN=5000005;
int n,m,i,j,k=3,x,y,a[MAXN],b[MAXN];
//x is the quantity of "reducing potions", y is the minimum cost, and b is used for bucket sorting 
inline void read(int &x)   //Read quickly 
{
	short negative=1;
    x=0;
    char c=getchar();
    while(c<'0' || c>'9')
    {
    	if(c=='-')
			negative=-1;
		c=getchar();
	}
    while(c>='0' && c<='9')
        x=(x<<3)+(x<<1)+(c^48),c=getchar();
    x*=negative;
}
inline void print(int x)   //Lose 
{
    if (x<0)
        putchar('-'),x=-x;
    if (x>9)
        print(x/10);
    putchar(x%10+'0');
}
signed main(void)
{
	read(n),read(m);
	for (i=1;i<=n;i++)
		read(a[i]),b[a[i]]++;
	for (i=1;i<=30000;i++)   //Bucket sorting 
		while (b[i])
			a[++j]=i,b[i]--;
	for (i=1;i<=n;i++)
	{
		bool f=false;
		while (a[i]>k)    //When you have to use "shrink potion" 
		{
			if (m<=0) //Try to give full play to the effect of "reducing potion", and exit at the end of one time, rather than when m is less than or equal to 0 
			{
				f=true;
				break;
			}
			x++,y++,k+=3;   //Use the shrink potion once
		}
		if (f)
			break;
		y+=(a[i]<k)?1:4;    //Judge whether it's 1 fee or 4 fee 
		m-=(a[i]%3)?(a[i]%3):3;    //Here, the buckle is directly from m 
	}
	if (m>0)   //Pulled all the attendants or A didn't storm it 
		return printf("Human Cannot Win Dog"),0;
	for (i=1;i<=n && m<0;i++)
		if (a[i]%3==0 && a[i]<=k && m+3<=0)
			y-=4,m+=3;
	for (i=1;i<=n && m<0;i++)
		if (a[i]%3==1 && a[i]<=k && m+1<=0)
			y-=1,m+=1;
	for (i=1;i<=n && m<0;i++)
		if (a[i]%3==2 && a[i]<=k && m+2<=0)
			y-=1,m+=2;
	//First 3, then 2, and finally 1
	print(x),putchar(' '),print(y);
	return 0;
} 

Time complexity of top ten sorting algorithms

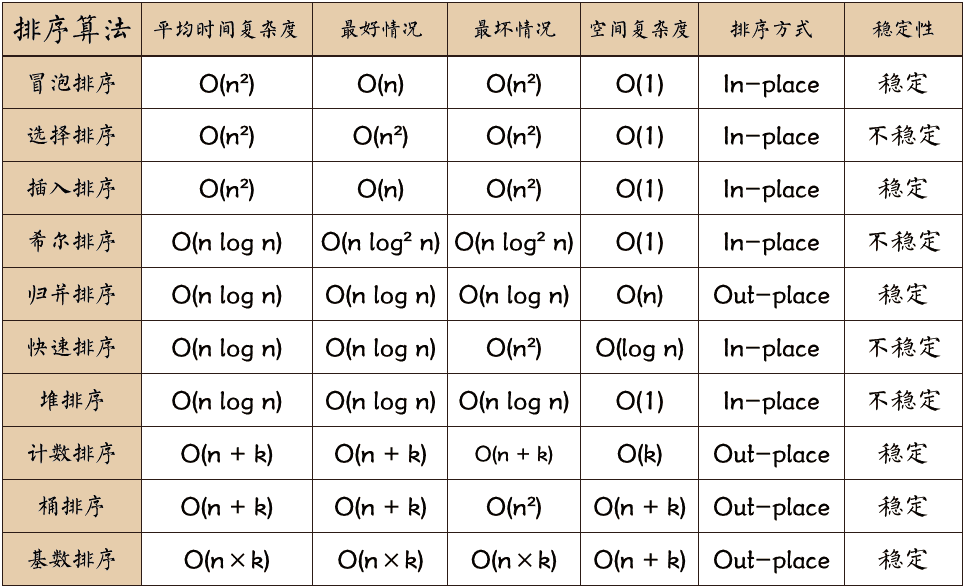
Conclusion:

Due to my limited ability, if there are errors in the article, please comment and correct. If this article is helpful to you, I hope to leave some praise and support. Thank you!