Foreword: in the last article, we learned the sequence table and found that we have a certain grasp of the concept of the sequence table, but after learning the sequence table, we found that there are some places that we can't do better or difficult to do, so we have a linked list. This article will take you into the study of the linked list!

Each picture:

Rush

1, Linked list

For some tasks and shortcomings that cannot be realized in the sequential list, we can implement or improve them in the linked list.

1. Concept and structure of linked list

Linked list is a discontinuous storage structure in physical storage structure. The logical order of data elements is realized through the reference link order in the linked list.

In practice, the structure of linked list is very diverse:
1. Unidirectional and bidirectional
2. Take the lead or not
3. Circulation and non circulation

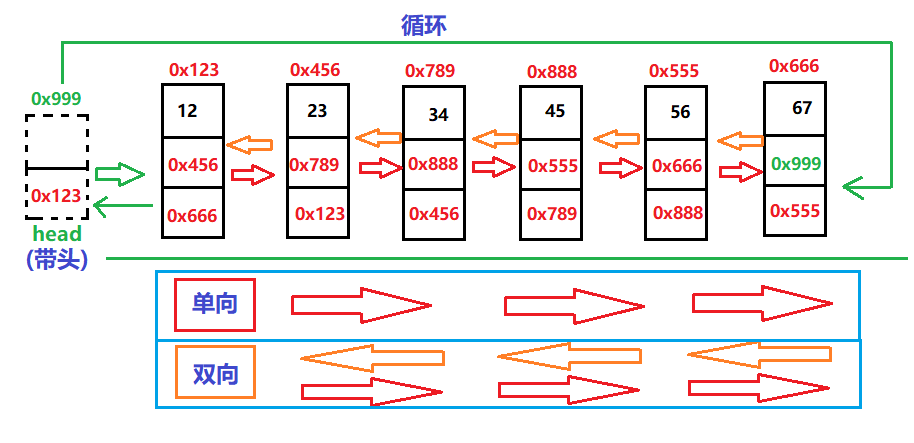
Combined with the above, there are 8 linked list structures:

one-way	two-way
Unidirectional head cycle	Bidirectional head cycle
Unidirectional non leading cycle	Bidirectional non leading cycle
Unidirectional non cyclic	Bidirectional non cyclic
Unidirectional acyclic	Bidirectional acyclic

For these eight linked list structures, here we only learn one-way non leading non cyclic and two-way non leading non cyclic, because these two are the most commonly used, including examinations and interviews.

So what is one-way, two-way, take the lead, do not take the lead, do not follow the cycle, let's explain one by one:

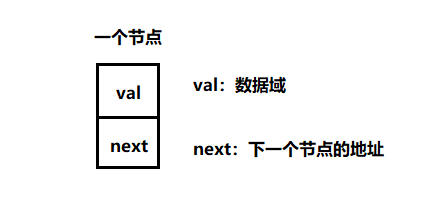
First of all, as for the linked list, it is composed of something called a node.

One way non leading acyclic linked list:

For a one-way linked list, each node will have two fields, one is the val data field and the other is next, which stores the address of the next node.

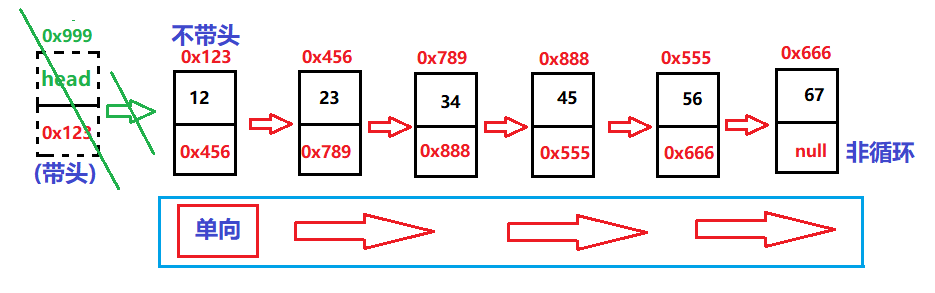
Then the linked list is composed of multiple nodes, so let's assume that some data form a linked list, and the linked list is one-way, not acyclic.

From here we can learn:

One way or two-way, in fact, depends on the next field of the linked list. When it flows in only one direction, it is one-way, and two are two-way.

Taking the lead and not taking the lead depends on whether the first node is a fixed head node and a fixed head node that cannot be moved. When we insert a node, it will still be in the first place. If we do not take the lead, we can insert it arbitrarily. If there is no fixed node, it will not take the lead.

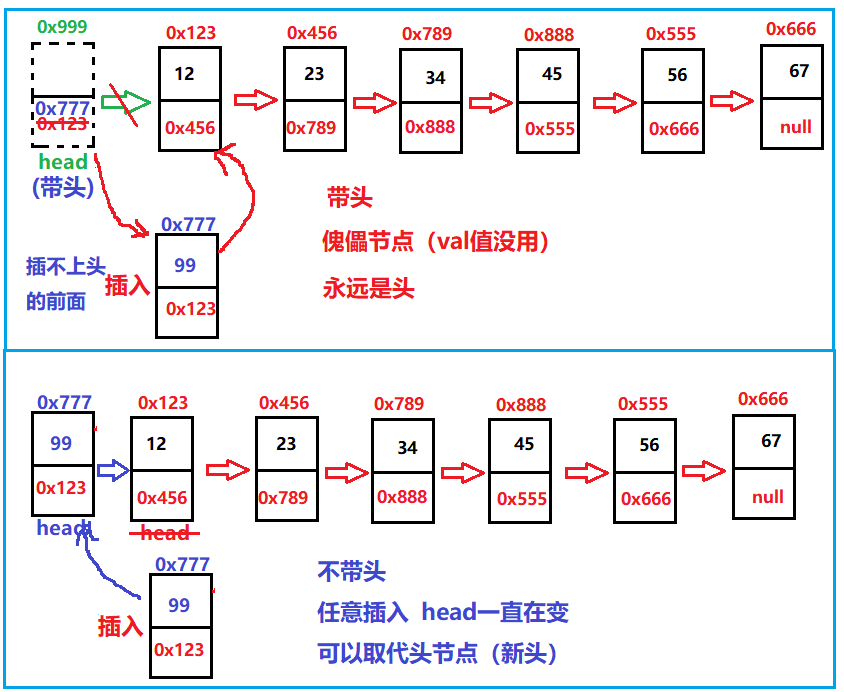
When we define a one-way non leading acyclic linked list, we have some nodes and storage addresses that are more convenient for us to use:

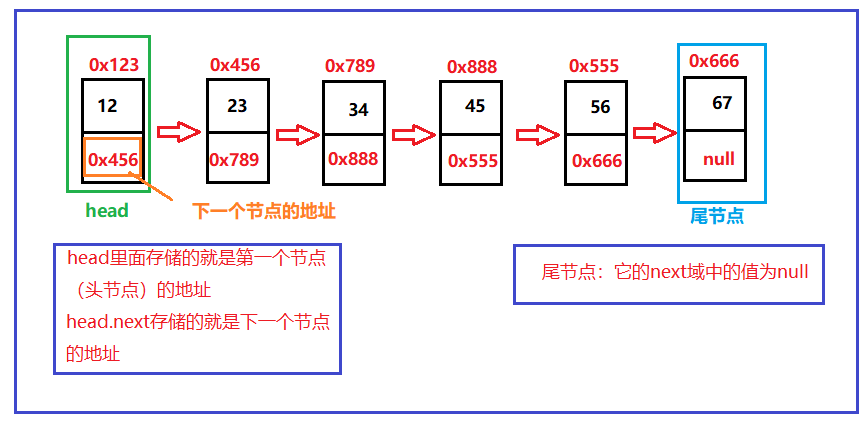
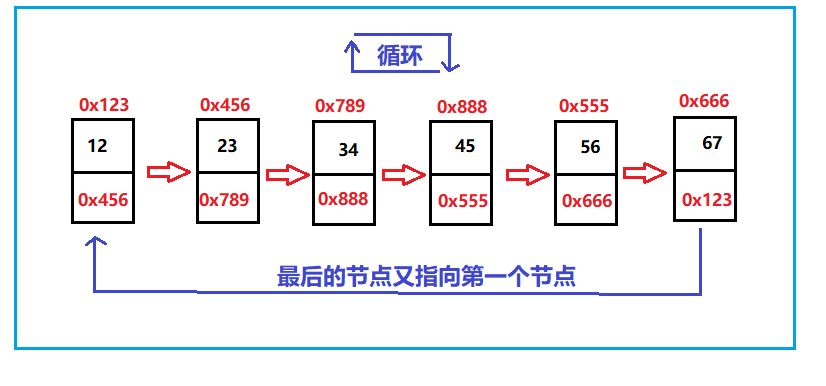
Loop and acyclic are the same. Let's see whether the address of the head node is stored in the next field of the last node in the linked list. If it is not or null, it is acyclic.

When we implement it in code, it is like this: create a new Java calss called TestDemo (hereinafter referred to as test), and a MyLinkedlist (hereinafter referred to as list). Test is used to store test cases, and list is used to write code for test:

//In TestDemo
public class TestDemo {
      ListNode listNode = new ListNode();
      //Create a new linked list
}

//In MyLinkedlist

class ListNode{
//Create a node class
    int val;//val domain
    ListNode next;//next domain

    public  ListNode(int val){
        this.val = val;//Construct a method to transfer the input in test to val
    }

    public ListNode head;//Head node
 
 public static void main(String[] args) {
        ListNode listNode = new ListNode(12);
        //Create a node. The val value is 12. next is not initialized. It is null by default
    }
     
}

This is the structure of the linked list and the initialization of nodes.

2. Implementation of linked list

For us, the nodes in the linked list will be created, so how to connect them? That is, list them one by one like the figure above, and then realize the function.

a) One way non leading linked list

Then, we also make a list of the functions we want to realize without taking the lead in the one-way linked list (of course, you can also add the functions you want to realize to it).

public class SingleLinkedList {
     //Print single linked list
     public void display();
     
     //Empty linked list
     public void clear();
     
     //Find out whether the keyword is included and whether the key is in the single linked list
     public boolean contains(int key);
     
     //Delete the node whose keyword is key for the first time
     public void remove(int key);
     
     //Delete all nodes with the value of key
     public void removeAllKey(int key);
     
     //Get the length of the single linked list
     public int size();
    
     
     //Head insertion
     public void addFirst(int data);
     
     //Tail interpolation
     public void addLast(int data);
     
     //Insert at any position, and the first data node is subscript 0
     public boolean addIndex(int index,int data);
     
     
 }

Next, we explain and implement one by one.

① Create linked list

We use the exhaustive method, which is not recommended, but it is easy to understand, so let's list it first with the exhaustive method to let you understand the linked list structure, and then we will write some methods to create it.

We can write a method to create nodes in the list class, enumerate them one by one, and then reference their next after creation, and assign the address of the next node to next. Then set the first node as the head node.

 public void createList() {
            //Create node 
            ListNode listNode1 = new ListNode(12);
            ListNode listNode2 = new ListNode(23);
            ListNode listNode3 = new ListNode(34);
            ListNode listNode4 = new ListNode(45);
            ListNode listNode5 = new ListNode(56);
            ListNode listNode5 = new ListNode(67);
            //Link node
            listNode1.next = listNode2;
            listNode2.next = listNode3;
            listNode3.next = listNode4;
            listNode4.next = listNode5;
            listNode5.next = listNode6;
            //listNode6 itself is null
            this.head = listNode1;//Set header node
    }

② Print linked list val value

Then, after the creation, we want to see what to do. Let's write a method called display, whose function is to print the val value of our linked list.

 public void display() {
        
        ListNode cur = this.head;//Instead of head node traversal
        while (cur != null) {
        //When cur is not null, it means that the linked list has not reached the end
            System.out.print(cur.val+" ");
            //Print val value
            cur = cur.next;
            //Jump to the next node
        }
        System.out.println();
    }

Don't worry. We have a diagram. For cur = cur.next, this is the key of the whole code. Jump to the next node by referring to the value of the next node stored by yourself, and then traverse and print:

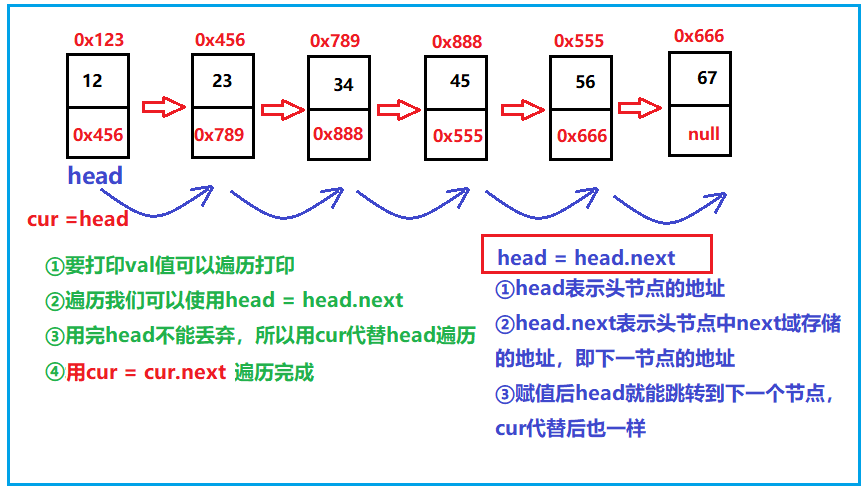
This is the val value of the print linked list.

③ Find whether the keyword key is included

We can also use cur to traverse whether to find the keyword key. If there is this value, we will return true and end. If not, false will be returned after traversal.

Code implementation:

 //Find out whether the keyword is included and whether the key is in the single linked list
    public boolean contains(int key){
        ListNode cur = this.head;//Get header node address
        
        while (cur != null) {
        //Loop traversal
            if(cur.val == key) {
            //Return true if any
                return true;
            }
            cur = cur.next;
            //Find the next one
        }
        return false;
         //Return false if no
    }

In this way, you can directly query whether the value of key exists.

④ Get the length of the single linked list

The length of the single linked list is the same, that is, traverse cur and record it every time, that is, set a variable every time + +, end when cur is empty, and finally return.

  //Get the length of the single linked list
    public int size(){
        int count = 0;
        ListNode cur = this.head;
        while (cur != null) {
            count++;
            cur = cur.next;
        }
        return count;
    }

⑤ Head insertion

We have implemented several simple functions. I believe you are familiar with the linked list. Here we write a method to add (insert) nodes - header insertion. Head interpolation, as the name suggests, is to put nodes from the beginning. If there are no nodes, we should also consider this problem. Then, if there is no node, it means that we are starting to create a linked list, so with this method, we can give up the above exhaustive method (of course, you can also use it if you like).

For the head insertion method, the node is inserted into the head. We should pay attention to how the new node is associated with the linked list and how the new node becomes the head.

Next, implement it directly with code:

 public void addFirst(int data){
        ListNode node = new ListNode(data);
        node.next = this.head;//Node gets the address of the next node
        this.head = node;//Node becomes the new head node
    }

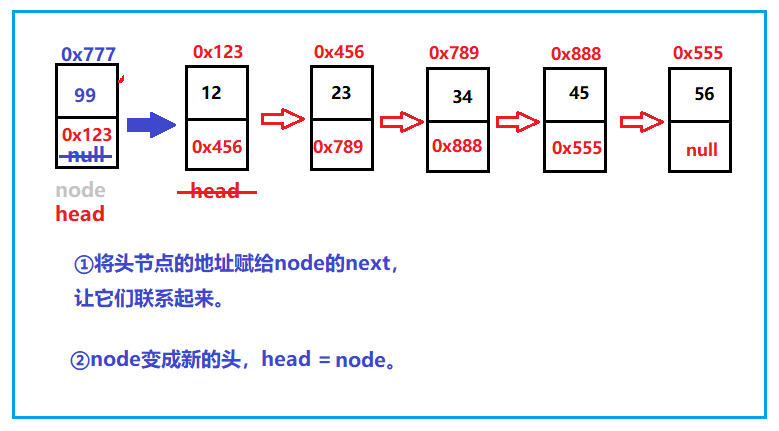
In fact, two situations are considered at the beginning. The first is to add a node when there is a node. Just like the above, the second is to add no node. When adding the first node, you need to judge whether there is no next node address. In fact, when there is no node, the obtained head is also null, and the head will become a node, So you can combine two pieces of code:

 public void addFirst(int data){
         if(this.head == null) {
            this.head = node;
         }else {
           node.next = this.head;
           this.head = node;
}

⑥ Tail interpolation

A head has a tail, so we also have tail insertion. Let's learn the tail interpolation method.

The tail interpolation method is also similar to the head interpolation method, that is, you need to find the tail node first, and then assign the address of the added node to the tail node.

Code implementation:

    public void addLast(int data){
        ListNode node = new ListNode(data);//New node

        if(this.head == null){
            //Determine whether the linked list is empty
            this.head=node;
        }
        else{
            ListNode cur = this.head; 
            while(cur.next != null){
                cur = cur.next;
            }
            cur.next = node;
        }
        
    }

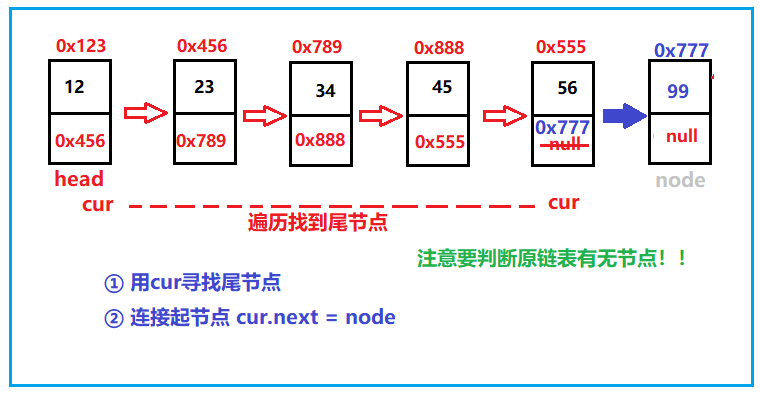
⑦ Insert at any position, and the first data node is subscript 0

If we insert it casually here, we have more things to consider. Because it is a random insertion, we should also consider the two cases of head insertion and tail insertion, and then there is the middle insertion method. But we have written these two methods before, so we can call the methods written above directly.

To find the node location, we can first write a method to make the code easier to read and write:

//Find a node before insertion
public ListNode findIndex(int index) {
                       //Enter find location
        ListNode cur = this.head;//cur works instead of head
        while (index-1 != 0) {
              //First position
            cur = cur.next;//No, just next
            index--;//Minus one digit
        }
        return cur;//Return to find the previous node before inserting
    }

Then there is the inserted code. Let's review the logic:

1. Judge whether the index is within the range (we can use the previous method to calculate the length of the linked list)
2. Judge whether it is head insertion and tail insertion (you can use our previous method)
3. Change the address if it's not clear (see the following code and view)

//Insert at any position, and the first data node is subscript 0
    public void addIndex(int index,int data){
        if(index < 0 || index > size()) {
        //Judge whether the location is legal
            System.out.println("index Illegal location!");
            return;
        }
        if(index == 0) {
        //Is it a head plug
            addFirst(data);
            return;
        }
        if(index == size()) {
        //Is it tail insertion
            addLast(data);
            return;
        }
        //It's not just transposition
        ListNode cur = findIndex(index);//Find previous node location
        ListNode node = new ListNode(data);//Node address to be inserted
        node.next = cur.next;//Insert the next address to the node
        cur.next = node;//The address of the inserted node is given to the previous node
        //So we can collude
    }

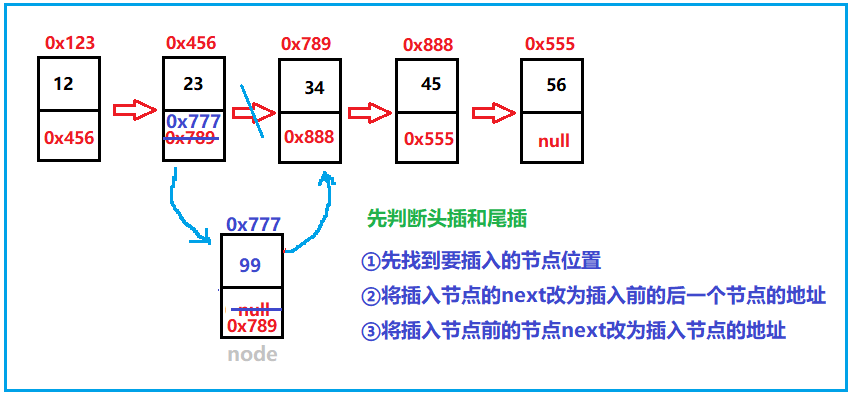
This is random insertion.

⑧ Delete the node with the value of key for the first time

We can add, but delete. In fact, for deletion, we only need to skip the node to be deleted, that is, give the next value of the node to be deleted to the previous node, and the previous node directly skips the deleted node and points to the next node.

Then we first find the previous node of the deleted node, so we also write a code searchPerv method to find the precursor of the keyword to be deleted:

public ListNode searchPerv(int key) {
        ListNode cur = this.head;//
        while (cur.next != null) {
        //Ergodic loop
            if(cur.next.val == key) {
                //When the next val value of the node finds the key
                return cur;//Return cur
            }
            cur = cur.next;//If it cannot be found, go to the next node
        }
        return null;
    }

Then, after finding it, it's about changing the next value. But before deleting, we should also consider the status of the linked list. First, whether it is empty. If it is empty, we can't delete it. Then see if it is a head node, because it is a head node that needs to change its head. Then it can't be deleted without this node. The last is the deletion operation.

Code implementation:

//Delete the node whose keyword is key for the first time
    public void remove(int key){
        if(this.head == null) {
        //It is empty and cannot be deleted!
            System.out.println("The single linked list is empty and cannot be deleted!");
            return;
        }
        if(this.head.val == key) {
        //Is the deletion of the header node
            this.head = this.head.next;
            return;
        }
        ListNode cur = searchPerv(key);
        if(cur == null) {
        //Without this node
            System.out.println("There is no node you want to delete!");
            return;
        }
        //The instructions have been considered from implementation to implementation, so they can be deleted.
        ListNode del = cur.next;
        cur.next = del.next;
    }

⑨ Delete all nodes with the value of key

Since the deletion of one key is done, how can we implement the method of deleting multiple keys? Is it a circular deletion method? It's OK, but the time complexity of the code is too large. What we want is to complete the circular deletion at one time.

First, let's consider the deletion of multiple nodes:

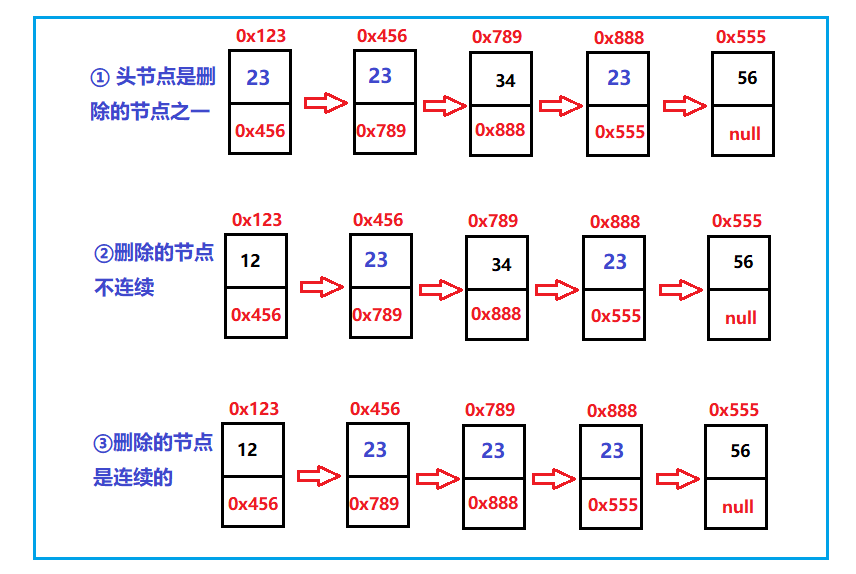
Why? First of all, if the head node needs to change its head, the deletion of one above has also been considered. Then, if it is discontinuous, just like the single deletion above, just take the address of the next field directly, while for continuous deletion, you need to jump to the address all the time. And some linked lists are empty.

When deleting the address, we first create two references, prev and cur. Prev is used to retain the previous address and cur is used to explore the way:

analysis:

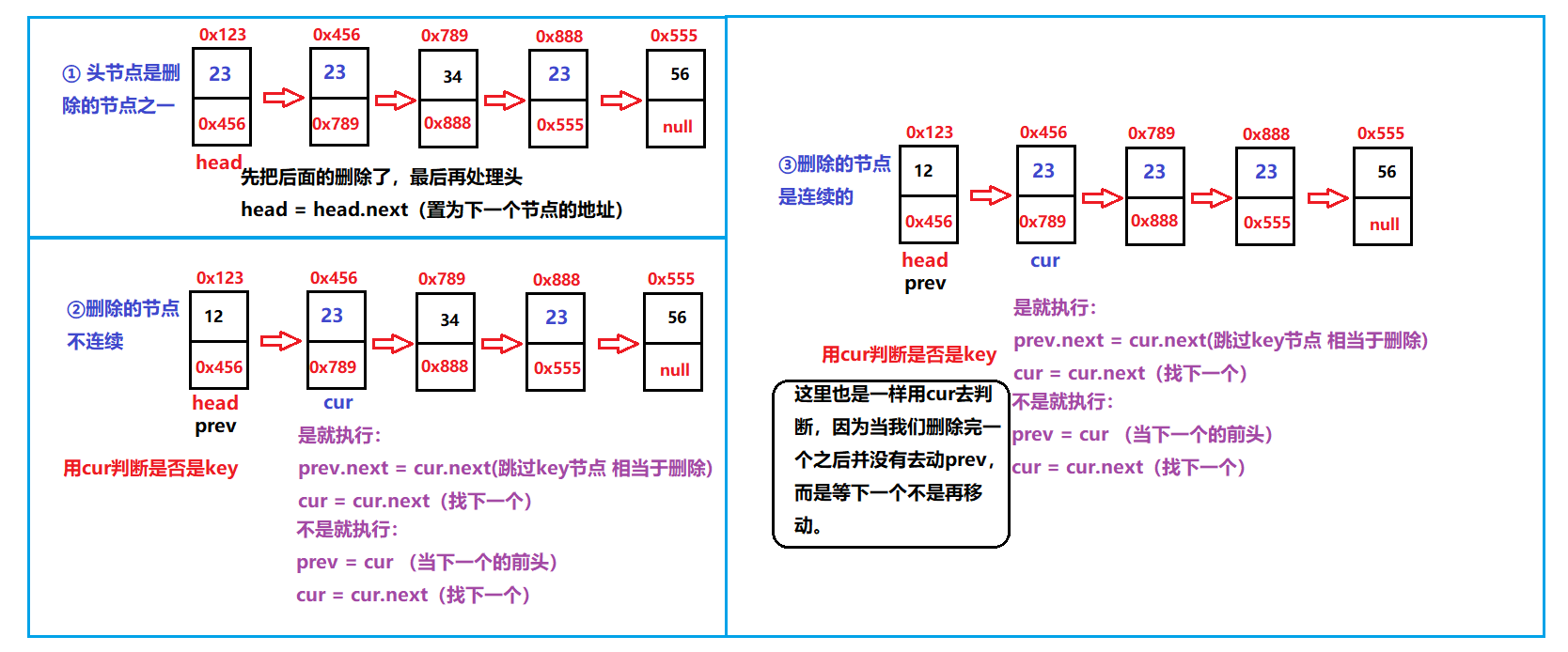
So we get the following code:

 //Delete all nodes with the value of key
    public ListNode removeAllKey(int key){
        if(this.head == null) return null;
        //It's empty. Don't delete it
        ListNode prev = this.head;
        ListNode cur = this.head.next;
        while (cur != null) {
        //Loop traversal
            if(cur.val == key) {
            //If yes, delete it
                prev.next = cur.next;
                cur = cur.next;
            }else {
            //No, just next
                prev = cur;
                cur = cur.next;
            }
        }
        //Final processing head
        if(this.head.val == key) {
            this.head = this.head.next;
        }
        return this.head;
    }

This is to delete all key s.

⑩ Empty linked list

The last code is to clear the linked list. Here we have a rough method. Don't we start from the first node when we enter the linked list? Then I directly set the head node to empty and disconnect all the links of the following nodes, which is equivalent to clearing the linked list.

code:

public void clear(){
       this.head == null;    
    }

But we can also be less rude. Don't we want to empty the linked list? How do we start and end, and restore them back to separate nodes so that they have no contact. However, once we set null, we will be disconnected from the following ones, so we should take precautions first, then write a reference, point to the front first, set null, and then catch up.

Code implementation:

public void clear(){
        while (this.head != null) {
        //You can use the head directly here. Anyway, delete the library and run away
            ListNode curNext = head.next;//a guide
            this.head.next = null;//Set null
            this.head = curNext;//keep pace with
        }
    }

2, The difference and relation between sequential list and linked list

In short:

Sequence table: a white cover a hundred ugly

White: continuous space, support random access
Ugly: the insertion and deletion time complexity of the middle or front part is O(N), and the cost of capacity expansion is relatively large.

Linked list: one (fat black) destroys all

Fat black: it is stored in nodes and does not support random access
All: 1. The time complexity of inserting and deleting at any position is O (1). 2. There is no capacity increase problem. Insert one to open up a space.

This is the whole content of the drawing in Java that takes you from the sequence list to the linked list 1. If you think it's good or helpful to you, you might as well like to pay attention to one key three links. In the next article, let's go to the question bank and touch the OJ linked list questions!!! Welcome to pay attention. Study together and work together! You can also look forward to the next blog of this series.

Link: It's all here! Java SE takes you from zero to a series

There is another thing: