subject

Problem solving ideas

Firstly, the idea of two-dimensional to one-dimensional is discussed.
Convert each point to abscissa multiplied by N + ordinate. It seems that it can be realized, but this problem needs four points, so 3 and 4 are implicitly connected. So it will be Wa.

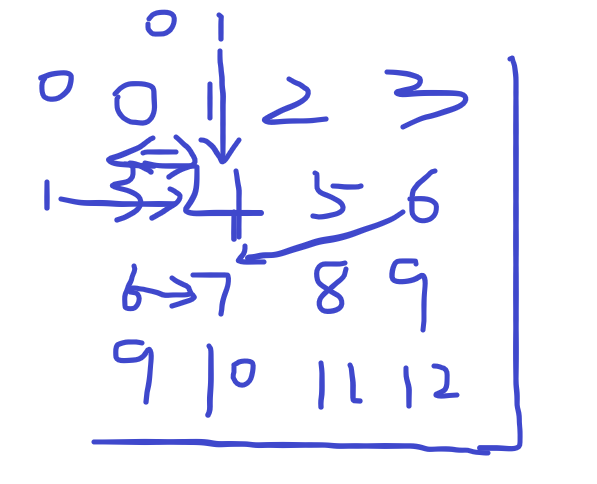
When we first increase N by 1, each available XY will not have the above implicit connection. (TIPS)

Then back to this question, when a 1 becomes 0, the surrounding 1 will also become 0, that is, the chain reaction.
So we can connect each point with this relationship into a block.
If you want to change all 1 to 0, you must press one of each connected block.
Suppose there are N connected blocks, and each connected block has A1, A2... an points.
This choice is N!a1a2*a3…*an.
Select one connected block at a time, and then select a point from the connected block.

In this way, we can preprocess the current answer.

Then deal with the modification problem.

First, changing 1 to 1 does not affect the answer. Direct output.

Changing 0 to 1 may connect several connected blocks together or add only one connected block.
If the classification is discussed, the code will become very complex and long.
It's better to consider generality, connect one and change the answer once.
When it changes from 0 to 1, first set cnt + +, and then update the answer (multiply by the new number). (that is, suppose he just adds a block.)
Then, for each connected one, divide the number first, then divide the product, and finally multiply it back to the sum according to the above formula. Then connect the connected blocks.
Because the previous answer may be modular (factorial is terrible), but division cannot guarantee modular congruence. So we're going to use the inverse element to turn division into multiplication.
Final output.

This is a good topic and I have learned a lot.

AC code

#include <bits/stdc++.h>
//#include <unordered_map>
//priority_queue
#define PII pair<int,int>
#define ll long long

using namespace std;

const  int  INF =  0x3f3f3f3f;
const  int mod = 1e9 + 7 ;
const  int N = 510 ; 

int n ;
int cnt = 0 ;
char mp[N][N] ; 
int a[N*N] ; 
int sz[N*N] ; 
int dx[4] = {0,0,-1,1} ;
int dy[4] = {1,-1,0,0} ;

long long qsm(long long a, long long b)
{
    long long ans = 1, t = a;
    while(b)
    {
        if (b & 1) ans = ans *t % mod;
        t = t * t % mod;
        b >>= 1;
    }
    return ans % mod;
}
long long ni(long long x )
{
    return qsm(x,mod-2) ; 
}
int find(int x )
{
    if (a[x] != x ) a[x] = find(a[x]);
    return a[x] ; 
}
void uio(int x ,int y )
{
    int fx = find(x) ;
    int fy = find(y) ; 
    if (fx != fy )
    {
        a[fy] = fx  ;
        sz[fx] += sz[fy] ; 
    }
}

int main()
{
    ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
    int n ;
    cin >> n ;
    for (int i = 1 ; i <= n ; i++ )
        cin >> mp[i] + 1 ;
    for (int i = 0 ; i <= n*n ; i++ )
    {
        a[i] = i ;
        sz[i] = 1 ; 
    }
    for (int i = 1 ; i <= n ; i++ )
    {
        for (int j = 1 ; j <= n ; j++ )
        {
            if (mp[i][j] == '1')
            {
                if (mp[i-1][j] == '1')
                    uio(i*n+j,(i-1)*n+j);
                if (mp[i][j-1] == '1')
                    uio(i*n+j,i*n+j-1);
                if (mp[i+1][j] == '1')
                    uio(i*n+j,(i+1)*n+j);
                if (mp[i][j+1] == '1')
                    uio(i*n+j,i*n+j+1);
            }
        }
    }
    long long  cnt = 0 ; 
    long long ans = 1 ; 
    for (int i = 1 ; i <= n ; i++ )
    {
        for (int j = 1 ; j <= n ; j++ )
        {
            if (a[i*n+j] == i*n+j && mp[i][j] == '1' )
            {
                cnt ++ ; 
                ans = (sz[i*n+j]*ans )% mod  ; 
            }
        }
    }
    for (int i = 1 ; i <= cnt ; i++ )
    {
        ans = (ans * i) %mod ; 
    }
    int k ;
    cin >> k ;
    for (int i = 1 ; i <= k ; i++ )
    {
        int  t1 , t2 ;
        cin >> t1 >> t2 ; 
        t1++,t2++;
        if (mp[t1][t2] == '1')
        {
            cout << ans << "\n" ; 
            continue ;
        }
        cnt ++ ;
        ans = ans * cnt % mod ; 
        mp[t1][t2] = '1' ;
        for (int j = 0 ; j < 4 ; j++ )
        {
            int fx = t1 + dx[j] ;
            int fy = t2 + dy[j] ; 
            if (mp[fx][fy] == '1')
            {
                int k1 = find(fx*n+fy) ;
                int k2 = find(t1*n+t2) ; 
                if (k1 != k2 )
                {
                    ans = ans*ni(cnt) % mod ; 
                    ans = ans*ni(sz[k1]) % mod ; 
                    ans = ans*ni(sz[k2]) % mod ; 
                    ans = ans*(sz[k1]+sz[k2]) %mod ;
                    cnt--;
                    uio(k1,k2) ;
                }
            }
        }
        cout << ans << "\n" ; 
    }
    
    return 0 ;
}