Bubble sorting

Start from the first element of the sequence to be sorted, constantly compare the values of adjacent elements, exchange if it is found that the reverse order, and gradually move the elements with larger values from front to back.

Every time the maximum value of the sequence to be sorted is found, the maximum value is fixed at the tail of the sequence to be sorted. Every time a maximum value of the sequence to be sorted is found, it needs to be cycled once, and N values need to be cycled n times. However, the last value does not need to be compared, it actually needs to be cycled n-1 times, that is, I < arr.length - 1.

public void bubbleSort (int[] arr) {
    for (int i = 0; i < arr.length - 1; i++) {
        for (int j = 0; j < arr.length - i - 1; j++) {
            if (arr[j] > arr[j + 1]) {
                int temp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = temp;
            }
        }
    }
}

Of course, this method can also be optimized.

Define a boolean variable flag to mark whether each round has been exchanged. Set flag to false at the beginning of each round of traversal. If the current round is not exchanged, that is, the flag is still false, it indicates that the array has been arranged in ascending order. At this time, the outer loop exits directly and the sorting ends.

public void bubbleSort (int[] arr) {
    boolean flag = false;
    for (int i = 0; i < arr.length - 1; i++) {
        flag = false;
        for (int j = 0; j < arr.length - i - 1; j++) {
            if (arr[j] > arr[j + 1]) {
                int temp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = temp;
                flag = true; //The round is swapped
            }
        }
        if (!flag) {
            break; //Array already ordered
        }
    }
}

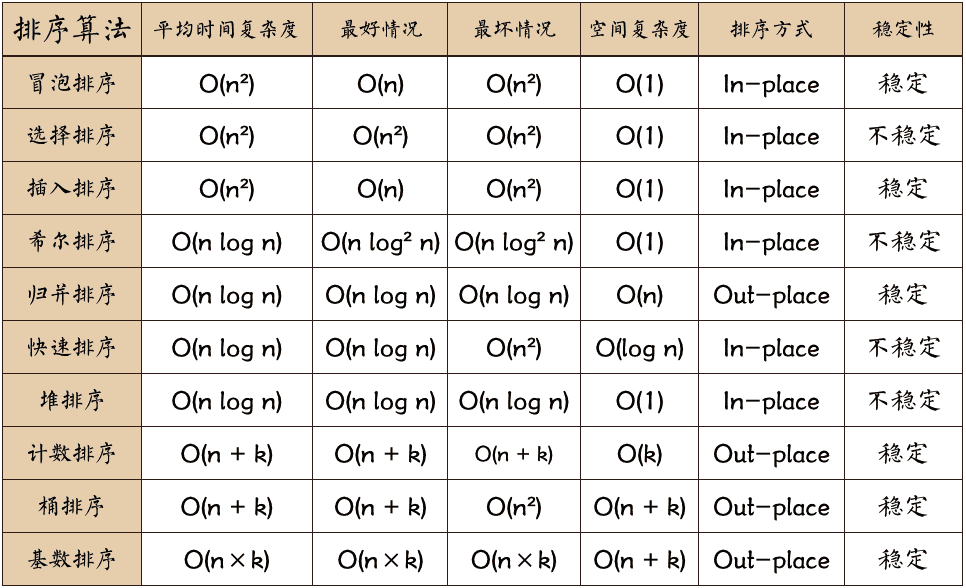
Complexity analysis:

• Time complexity O(n^2)
• Space complexity O(1)
• stable

Select sort

Selecting sorting will find the smallest element from the unordered interval each time and put it at the end of the sorted interval. Similarly, selecting sorting also needs to compare n - 1 rounds, and there is no need to compare the last round.

public void selectSort (int[] arr) {
    for (int i = 0; i < arr.length - 1; i++) {
        int minIndex = i; //Initialize minimum index
        for (int j = i + 1; j < arr.length; j++) {
            if (arr[j] < arr[minIndex]) {
                minIndex = j;
            }
        }
        if (minIndex != i) {
            int temp = arr[i];
            arr[i] = arr[minIndex];
            arr[minIndex] = temp;
        }
    }
}

Complexity analysis:

• Time complexity O(n^2)
• Space complexity O(1)
• instable

Direct insert sort

The n elements to be sorted are regarded as an ordered table and an unordered table. At the beginning, the ordered table contains only one element, and the unordered table contains n-1 elements. In the sorting process, the first element is taken out from the unordered table every time, compared with the elements in the ordered table, and inserted into the appropriate position in the ordered table to make it a new ordered table.

public void insertSort (int[] arr) {
    for (int i = 1; i < arr.length; i++) {
        int temp = arr[i]; //Record the value to be sorted
        int j = i;
        while (j > 0 && arr[j - 1] > temp) {
            arr[j] = arr[j - 1];
            j--;
        }
        if (j != i) {
            arr[j] = temp;
        }
    }
}

Complexity analysis:

• Time complexity O(n^2)
• Space complexity O(1)
• stable

Shell Sort

Hill sort, also known as decreasing incremental sort, is an improved version of direct insertion sort. Possible problems in simple insertion sorting: when the number of inserts is small, the number of backward moves increases significantly, which has an impact on the efficiency.

public void shellSort(int[] arr) {
    int length = arr.length;
    for (int step = length / 2; step >= 1; step /= 2) {
        for (int i = step; i < length; i++) {
            int temp = arr[i];
            int j = i - step;
            while (j >= 0 && arr[j] > temp) {
                arr[j + step] = arr[j];
                j -= step;
            }
            arr[j + step] = temp;
        }
    }
}

Complexity analysis:

• Time complexity O(nlogn)
• Space complexity O(1)
• instable

Merge sort

The core idea of merging and sorting is divide and conquer, which divides a complex problem into several sub problems to solve.

The idea of merging sorting algorithm is to divide the array into two sub arrays from the middle, and recursively divide the sub array into smaller arrays. Sequences with a length of 1 are ordered, so they should be decomposed recursively until there is only one element in the subarray. The sorting method is to merge two elements in size order. Then return in recursive order, and continue to merge the ordered arrays until the whole array is ordered.

public static void mergeSort(int[] source, int[] temp, int left, int right) {
    if (left >= right) {
        return;
    }
    int mid = (left + right) / 2;
    mergeSort(source, temp, left, mid);
    mergeSort(source, temp, mid + 1, right);
    int i = left, j = mid + 1, k = 0;
    while (i <= mid && j <= right) {
        if (source[i] <= source[j]) {
            temp[k++] = source[i++];
        } else {
            temp[k++] = source[j++];
        }
    }
    while (i <= mid) {
        temp[k++] = source[i++];
    }
    while (j <= right) {
        temp[k++] = source[j++];
    }
    for (i = left, j = 0; i <= right; i++, j++) {
        source[i] = temp[j];  //Copy back to the original array
    }
}

public static void main(String[] args) {
    int[] arr = {12, 3, 15, 55, 97, 6, 11, 41, 88, 12};
    int[] temp = new int[arr.length];
    mergeSort(arr, temp, 0, arr.length - 1);
    for (int i = 0; i < arr.length; i++) {
        System.out.println(arr[i]);
    }
}

Complexity analysis:

• Time complexity O(nlogn)
• Spatial complexity O(logn)
• stable

Quick sort

Quick sort also adopts the idea of divide and conquer. If merge sort is to split and then sort, then quick sort is to sort and then divide.

The basic idea of quick sort is: firstly, select a record from the waiting sequence, which is called hub, and divide the sequence of waiting sequence into two subsequences before and after the hub through the comparison between keywords and hub, in which all keywords of the subsequence before the hub are not greater than the hub, and all keywords of the subsequence after the hub are not less than the hub; At this time, the hub is in place, and then the two subsequences are recursively sorted in the same way, so as to make the whole sequence orderly.

public void quickSort(int[] arr, int left, int right) {
    if (left >= right) {
        return;
    }
    int pivot = arr[left];
    int i = left, j = right;
    while (i < j) {
        while (i < j && arr[j] >= pivot)
            j--;
        arr[i] = arr[j];
        while (i < j && arr[i] <= pivot)
            i++;
        arr[j] = arr[i];
    }
    arr[i] = pivot;
    quickSort(arr, left, i - 1);
    quickSort(arr, j + 1, right);
}

Complexity analysis:

• Time complexity O(nlogn)
• Spatial complexity O(n)
• instable

Heap sort

Heap sort is a sort algorithm designed by using heap data structure. Heap is a kind of complete binary tree with the following characteristics:

Large top heap: the value of each node is greater than or equal to the value of its left and right child nodes

Small top heap: the value of each node is less than or equal to the value of its left and right child nodes

[the external chain picture transfer fails. The source station may have an anti-theft chain mechanism. It is recommended to save the picture and upload it directly (img-swnhy2hv-16365585870113) (D: \ technical books and notes pictures \ notes pictures \ data structures and algorithms \ size top heap. png)]

Basic steps of heap sorting:

1. The array to be sorted is constructed into a large top heap, that is, the sinking operation is carried out from right to left and from bottom to top. At this point, the maximum value of the whole sequence is the root node at the top of the heap. Generally, large top pile is used in ascending order and small top pile is used in descending order
2. Swap it with the end element, where the end is the maximum.
3. The remaining n-1 elements are then adjusted and reconstructed into a heap. Then exchange the top element with the end element, and execute it repeatedly to get an ordered sequence.

The algorithm is distinguished by whether the index of the first element of the array is 0 or 1. The algorithm has the following two versions:

• The index of the first element of the array is 1

//Array cannot have element at position 0
public void heapSort(int[] arr) {
    int N = arr.length - 1;
    //Construction of large top reactor
    for (int i = N / 2; i > 0; i--) {
        sink(arr, i, N);
    }
    while (N > 1) {
        swap(arr, 1, N--);  //The heap top and tail nodes are exchanged, and the heap length is reduced by 1
        sink(arr, 1, N);  //Filter new heap top nodes
    }
}

private void sink(int[] arr, int pos, int N) {
    while (pos <= N / 2) {
        int j = 2 * pos;
        if (j < N && arr[j] < arr[j + 1]) {
            j++;    // j is the priority position of left and right children
        }
        if (arr[j] < arr[pos]){
            return;
        }
        swap(arr, pos, j);
        pos = j;
    }
}

private void swap(int[] arr, int i, int j) {
    int temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}

• The index of the first element of the array is 0

//There is an element at position 0 of the array
public static void heapSort(int[] arr) {
    int N = arr.length;
    //Construction of large top reactor
    for (int i = N / 2 - 1; i >= 0; i--) {
        sink(arr, i, N);
    }
    while (N > 1) {
        swap(arr, 0, --N);  //The heap top and tail nodes are exchanged, and the heap length is reduced by 1
        sink(arr, 0, N);  //Filter new heap top nodes
    }
}
//sink
private static void sink(int[] arr, int pos, int N) {
    while (pos <= N / 2 - 1) {
        int j = 2 * pos + 1;
        if (j < N - 1 && arr[j] < arr[j + 1]) {
            j++;    // j is the priority position of left and right children
        }
        if (arr[j] < arr[pos]){
            return;
        }
        swap(arr, pos, j);
        pos = j;
    }
}

private static void swap(int[] arr, int i, int j) {
    int temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}

Complexity analysis:

• Time complexity O(nlogn)
• Space complexity O(1)
• instable

Heap sort is an in place sort that does not take advantage of additional space.

Quicksort is the fastest general-purpose sorting algorithm. It has few inner loop instructions, and it can also use cache because it always accesses data sequentially. Modern operating systems rarely use heap sorting because it cannot cache using the principle of locality, that is, array elements are rarely compared and exchanged with adjacent elements. Using three-dimensional segmentation quick sorting, some distributed inputs that may appear in practical application can reach the linear level, while other sorting algorithms still need linear logarithmic time.

Count sort

The difference between comparison and non comparison

Common quick sort, merge sort, heap sort and bubble sort belong to comparative sort. In the final result of sorting, the order between elements depends on the comparison between them. Each number must be compared with other numbers to determine its position.
In bubble sort, the problem scale is n, and because it needs to be compared n times, the average time complexity is O(n) ²). In sorting such as merge sort and quick sort, the problem scale is reduced to logN times by divide and conquer, so the time complexity is O(nlogn) on average.
The advantage of comparative sorting is that it is suitable for data of all sizes and does not care about the distribution of data. It can be said that comparative sorting is applicable to all situations that need sorting.

Count sort, cardinality sort and bucket sort belong to non comparison sort. Non comparative sorting is to sort by determining how many elements should be before each element. For array arr, calculate the number of elements before arr[i], and uniquely determine the position of arr[i] in the sorted array.
Non comparative sorting can be solved by determining the number of existing elements before each element, and all traversals can be solved at one time. Algorithm time complexity O(n).
Non comparative sorting has low time complexity, but it takes up space to determine the unique location. Therefore, there are certain requirements for data scale and data distribution.

The core of counting sorting is to convert the input data values into keys and store them in the additional array space. As a sort with linear time complexity, count sort requires that the input data must be integers with a certain range.

Applicable conditions: counting and sorting takes up a lot of space. It is only applicable to the situation where the data is relatively concentrated, such as [0100], the scores of students in the college entrance examination.

//When the input element is n integers between 0 and k
public void countSort(int[] arr) {
    int maxValue = arr[0];
    //Get maximum
    for (int num : arr) {
        if (maxValue < num) {
            maxValue = num;
        }
    }
    int[] bucket = new int[maxValue + 1];
    for (int num : arr) {
        bucket[num]++;
    }
    for (int i = 0, j = 0; i <= maxValue; i++) {
        while (bucket[i]-- > 0) {
            arr[j++] = i;
        }
    }
}

Of course, the above is the most basic count sorting, and there can be optimization. For example, the length of the bucket array can be the difference between the maximum value and the minimum value + 1. It is not necessary that the data must start from 0.

Complexity analysis:

• Time complexity O(N+k)
• Spatial complexity O(k)
• stable

Bucket sorting

Bucket sorting is an upgraded version of counting sorting. It makes use of the mapping relationship of the function. The key to efficiency lies in the determination of the mapping function. In order to make bucket sorting more efficient, we need to do these two things:

1. Increase the number of barrels as much as possible with sufficient additional space
2. The mapping function used can evenly distribute the input N data into K buckets

At the same time, for the sorting of elements in the bucket, it is very important to choose a comparative sorting algorithm for the performance.

When is the fastest:

When the input data can be evenly distributed to each bucket.

When is the slowest:

When the input data is allocated to the same bucket.

public void bucketSort(int[] arr){
    // Calculate maximum and minimum values
    int max = arr[0];
    int min = arr[0];
    for(int num : arr){
       if (num > max) {
           max = num;
       } else if (num < min) {
           min = num;
       }
    }
    // Calculate the number of barrels
    int bucketNum = (max - min) / arr.length + 1;
    List<List<Integer>> bucketArr = new ArrayList<>(bucketNum);
    for(int i = 0; i < bucketNum; i++){
        bucketArr.add(new ArrayList<Integer>());
    }
    // The mapping function is used to allocate the data to each bucket
    for(int i = 0; i < arr.length; i++){
        int hash = (arr[i] - min) / (arr.length);
        bucketArr.get(hash).add(arr[i]);
    }
    // Sort each bucket
    for(int i = 0; i < bucketArr.size(); i++){
        Collections.sort(bucketArr.get(i));
    }
    // Assign the elements in the bucket to the original sequence
    int index = 0;
    for(int i = 0; i < bucketArr.size(); i++){
        for(int j = 0; j < bucketArr.get(i).size(); j++){
            arr[index++] = bucketArr.get(i).get(j);
        }
    }
}

Complexity analysis:

• Time complexity O(N)
• Space complexity O(N)
• stable

Cardinality sort

Cardinal sorting is a non comparative sorting algorithm. Its principle is to cut integers into different numbers according to the number of bits, and then compare them according to each number of bits.

Unify all values to be compared into the same digit length, and fill zero in front of the shorter digit. Then, start from the lowest order and sort once in turn. In this way, the sequence becomes an ordered sequence from the lowest order to the highest order.

public void radixSort(int[] arr) {
    //Define an array of buckets. There are 10 buckets in total. Each bucket is a one-dimensional array
    int[][] bucket = new int[10][arr.length];
    //Number of elements per bucket
    int[] bucketCount = new int[10];
    int maxValue = arr[0];
    //Get maximum
    for (int num : arr) {
        if (num > maxValue) {
            maxValue = num;
        }
    }
    //Get maximum number of digits
    int maxLength = (maxValue + "").length();
    //Sort on corresponding bits
    for (int digit = 0, n = 1; digit < maxLength; digit++, n*= 10) {
        for (int i = 0; i < arr.length; i++) {
            //Gets the value of the corresponding bit of the element
            int value = arr[i] / n % 10;
            bucket[value][bucketCount[value]++] = arr[i];
        }
        int index = 0;
        //Put the data in the bucket back into the original array
        for (int j = 0; j < 10; j++) {
            for (int k = 0; k < bucketCount[j]; k++) {
                arr[index++] = bucket[j][k];
            }
            bucketCount[j] = 0; // Clear 0
        }
    }
}

Complexity analysis:

• Time complexity O(N)
• Space complexity O(N)
• stable

Cardinality sort vs count sort vs bucket sort

These three sorting algorithms all use the concept of bucket, but there are obvious differences in the use of bucket:

• Counting and sorting: only one key value is stored in each bucket;
• Bucket sorting: each bucket stores a certain range of values;
• Cardinality sorting: allocate buckets according to each number of the key value;

summary

• When the data size is small, you can use direct insertion sorting.
• When the array is basically ordered at the beginning, you can use direct insertion sorting and bubble sorting.
• When the data scale is large, you can consider using quick sort, which is the fastest. When recording random distribution, the average time of quick sorting is the shortest.
• Heap sort requires less auxiliary space than quicksort, and there is no worst-case scenario for quicksort. Both sorts are unstable.
• If the sorting is required to be stable, merge sorting can be selected.