Thank you very much for reading this article~
Welcome[ 👍 [like][ ⭐ Collection][ 📝 [comments]~
It's not hard to give up, but it must be cool to insist~
I hope all of us can make a little progress every day~
This paper consists of White hat of the second leader: https://le-yi.blog.csdn.net/ Blog originality~
Sword finger Offer II 054. Sum of all values greater than or equal to nodes | 538. Convert binary search tree to accumulation tree | 1038. Convert binary search tree to accumulation tree:
Given a binary search tree, replace the value of each node with the sum of all node values greater than or equal to the node value in the tree.
Remind me that the binary search tree meets the following constraints:
- The left subtree of a node contains only nodes whose key is less than the node key.
- The right subtree of a node contains only nodes whose key is greater than the node key.
- The left and right subtrees must also be binary search trees.
Example 1
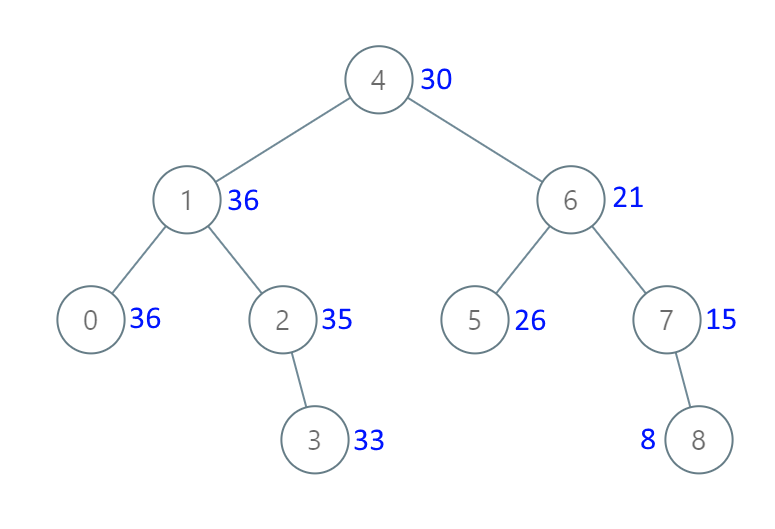
Input: root = [4,1,6,0,2,5,7,null,null,null,3,null,null,null,8] Output: [30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]
Example 2
Input: root = [0,null,1] Output: [1,null,1]
Example 3
Input: root = [1,0,2] Output: [3,3,2]
Example 4
Input: root = [3,2,4,1] Output: [7,9,4,10]
Tips
- The number of nodes in the tree is between 0 and 104.
- The value of each node is between - 104 and 104.
- All values in the tree are different from each other.
- The given tree is a binary search tree.
analysis
- This algorithm problem needs to be translated and easy to understand.
- Binary tree, you should be familiar with, is generally positive order traversal, medium order traversal, post order traversal, and then some simple logic in the process of traversal.
- Binary search tree is a special binary tree. The problem has been explained.
- Because the value of each node should be replaced by the sum of all node values greater than or equal to the node value in the tree, according to the characteristics of binary search tree, in fact, it is to replace the value of each node with its own value and accumulate the sum of the values of the right subtree.
- First of all, you need to traverse each node, but the order is the key. You will find that the normal positive order traversal, medium order traversal and post order traversal are not smooth.
- According to the meaning of the topic, it is obvious that the best order is to traverse the right subtree, then the root node, and then the left subtree. This is the most smooth. Only one variable needs to continuously accumulate the node value, accumulate the value of which node to traverse, and then assign it to this node. This is just the opposite of the middle order traversal, that is, the reverse middle order traversal.
- Traversing this doll structure is generally recursion or loop (using stack data structure). Recursion is relatively simple, but limited by the call stack. Loop actually simulates the call stack with a data structure such as stack, which is basically the same, but the number of calls can be more, because the space of the call stack is generally limited and the heap space is much larger, However, to achieve the same function, it is logically more complex.
- Whether you use recursion or stack data structure to cycle, you need additional memory space corresponding to the tree structure. There is a very clever traversal method called Morris traversal, which can reduce the space complexity of non recursive traversal to O (1). The specific implementation of the second leader has been annotated in detail. You can also go to the Encyclopedia for in-depth understanding.
Problem solution
java
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public TreeNode convertBST(TreeNode root) {
int sum = 0;
TreeNode cur = root;
while (cur != null) {
if (cur.right == null) {
// No child is worth more than himself
// It's your turn to deal with yourself
sum += cur.val;
cur.val = sum;
// I have traversed it myself, so I should traverse a smaller one than myself
cur = cur.left;
} else {
// On the far left of the right child, the youngest child older than himself
// That is, the last traversal node in front of you, and the next one should be yourself
TreeNode leftmostOfRight = cur.right;
while (leftmostOfRight.left != null
&& leftmostOfRight.left != cur) {
leftmostOfRight = leftmostOfRight.left;
}
if (leftmostOfRight.left == null) {
// No association has been done. It means that the current node is associated for the first time to ensure that it is your turn after traversing the smallest node larger than yourself
leftmostOfRight.left = cur;
cur = cur.right;
} else {
// The second traversal here shows that the larger ones are traversed
// Dissolve the relationship and restore the tree structure
leftmostOfRight.left = null;
// It's your turn to deal with yourself
sum += cur.val;
cur.val = sum;
// I have traversed it myself, so I should traverse a smaller one than myself
cur = cur.left;
}
}
}
return root;
}
}
c
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
struct TreeNode* convertBST(struct TreeNode* root){
int sum = 0;
struct TreeNode *cur = root;
while (cur != NULL) {
if (cur->right == NULL) {
// No child is worth more than himself
// It's your turn to deal with yourself
sum += cur->val;
cur->val = sum;
// I have traversed it myself, so I should traverse a smaller one than myself
cur = cur->left;
} else {
// On the far left of the right child, the youngest child older than himself
// That is, the last traversal node in front of you, and the next one should be yourself
struct TreeNode *leftmostOfRight = cur->right;
while (leftmostOfRight->left != NULL
&& leftmostOfRight->left != cur) {
leftmostOfRight = leftmostOfRight->left;
}
if (leftmostOfRight->left == NULL) {
// No association has been done. It means that the current node is associated for the first time to ensure that it is your turn after traversing the smallest node larger than yourself
leftmostOfRight->left = cur;
cur = cur->right;
} else {
// The second traversal here shows that the larger ones are traversed
// Dissolve the relationship and restore the tree structure
leftmostOfRight->left = NULL;
// It's your turn to deal with yourself
sum += cur->val;
cur->val = sum;
// I have traversed it myself, so I should traverse a smaller one than myself
cur = cur->left;
}
}
}
return root;
}
c++
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* convertBST(TreeNode* root) {
int sum = 0;
TreeNode *cur = root;
while (cur != nullptr) {
if (cur->right == nullptr) {
// No child is worth more than himself
// It's your turn to deal with yourself
sum += cur->val;
cur->val = sum;
// I have traversed it myself, so I should traverse a smaller one than myself
cur = cur->left;
} else {
// On the far left of the right child, the youngest child older than himself
// That is, the last traversal node in front of you, and the next one should be yourself
TreeNode *leftmostOfRight = cur->right;
while (leftmostOfRight->left != nullptr
&& leftmostOfRight->left != cur) {
leftmostOfRight = leftmostOfRight->left;
}
if (leftmostOfRight->left == nullptr) {
// No association has been done. It means that the current node is associated for the first time to ensure that it is your turn after traversing the smallest node larger than yourself
leftmostOfRight->left = cur;
cur = cur->right;
} else {
// The second traversal here shows that the larger ones are traversed
// Dissolve the relationship and restore the tree structure
leftmostOfRight->left = nullptr;
// It's your turn to deal with yourself
sum += cur->val;
cur->val = sum;
// I have traversed it myself, so I should traverse a smaller one than myself
cur = cur->left;
}
}
}
return root;
}
};
python
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def convertBST(self, root: TreeNode) -> TreeNode:
total = 0
cur = root
while cur:
if not cur.right:
# No child is worth more than himself
# It's your turn to deal with yourself
total += cur.val
cur.val = total
# I have traversed it myself, so I should traverse a smaller one than myself
cur = cur.left
else:
# On the far left of the right child, the youngest child older than himself
# That is, the last traversal node in front of you, and the next one should be yourself
leftmostOfRight = cur.right
while leftmostOfRight.left and leftmostOfRight.left != cur:
leftmostOfRight = leftmostOfRight.left
if not leftmostOfRight.left:
# No association has been done. It means that the current node is associated for the first time to ensure that it is your turn after traversing the smallest node larger than yourself
leftmostOfRight.left = cur
cur = cur.right
else:
# The second traversal here shows that the larger ones are traversed
# Dissolve the relationship and restore the tree structure
leftmostOfRight.left = None
# It's your turn to deal with yourself
total += cur.val
cur.val = total
# I have traversed it myself, so I should traverse a smaller one than myself
cur = cur.left
return root
go
/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func convertBST(root *TreeNode) *TreeNode {
sum := 0
cur := root
for cur != nil {
if cur.Right == nil {
// No child is worth more than himself
// It's your turn to deal with yourself
sum += cur.Val
cur.Val = sum
// I have traversed it myself, so I should traverse a smaller one than myself
cur = cur.Left
} else {
// On the far left of the right child, the youngest child older than himself
// That is, the last traversal node in front of you, and the next one should be yourself
leftmostOfRight := cur.Right
for leftmostOfRight.Left != nil && leftmostOfRight.Left != cur {
leftmostOfRight = leftmostOfRight.Left
}
if leftmostOfRight.Left == nil {
// No association has been done. It means that the current node is associated for the first time to ensure that it is your turn after traversing the smallest node larger than yourself
leftmostOfRight.Left = cur
cur = cur.Right
} else {
// The second traversal here shows that the larger ones are traversed
// Dissolve the relationship and restore the tree structure
leftmostOfRight.Left = nil
// It's your turn to deal with yourself
sum += cur.Val
cur.Val = sum
// I have traversed it myself, so I should traverse a smaller one than myself
cur = cur.Left
}
}
}
return root
}
rust
// Definition for a binary tree node.
// #[derive(Debug, PartialEq, Eq)]
// pub struct TreeNode {
// pub val: i32,
// pub left: Option<Rc<RefCell<TreeNode>>>,
// pub right: Option<Rc<RefCell<TreeNode>>>,
// }
//
// impl TreeNode {
// #[inline]
// pub fn new(val: i32) -> Self {
// TreeNode {
// val,
// left: None,
// right: None
// }
// }
// }
use std::rc::Rc;
use std::cell::RefCell;
impl Solution {
pub fn convert_bst(root: Option<Rc<RefCell<TreeNode>>>) -> Option<Rc<RefCell<TreeNode>>> {
let mut sum = 0;
let mut cur = root.clone();
while cur.is_some() {
if cur.as_ref().unwrap().borrow().right.is_none() {
// No child is worth more than himself
// It's your turn to deal with yourself
sum += cur.as_ref().unwrap().borrow().val;
cur.as_ref().unwrap().borrow_mut().val = sum;
// I have traversed it myself, so I should traverse a smaller one than myself
cur = cur.unwrap().borrow().left.clone();
} else {
// On the far left of the right child, the youngest child older than himself
// That is, the last traversal node in front of you, and the next one should be yourself
let mut leftmostOfRight = cur.as_ref().unwrap().borrow().right.clone();
while leftmostOfRight.as_ref().unwrap().borrow().left.is_some()
&& leftmostOfRight.as_ref().unwrap().borrow().left != cur {
leftmostOfRight = leftmostOfRight.unwrap().borrow().left.clone();
}
if leftmostOfRight.as_ref().unwrap().borrow().left.is_none() {
// No association has been done. It means that the current node is associated for the first time to ensure that it is your turn after traversing the smallest node larger than yourself
leftmostOfRight.unwrap().borrow_mut().left = cur.clone();
cur = cur.unwrap().borrow().right.clone();
} else {
// The second traversal here shows that the larger ones are traversed
// Dissolve the relationship and restore the tree structure
leftmostOfRight.unwrap().borrow_mut().left = Option::None;
// It's your turn to deal with yourself
sum += cur.as_ref().unwrap().borrow().val;
cur.as_ref().unwrap().borrow_mut().val = sum;
// I have traversed it myself, so I should traverse a smaller one than myself
cur = cur.unwrap().borrow().left.clone();
}
}
}
root
}
}