Recommended blog and video explanation

Heap sort (heap rebuild + insert + delete detailed explanation) UP Master: bald girl Wang pushed

Forward citation

I didn't get up until 10 o'clock today. I really don't know why I got up late. Of course, it's also the weekend, but I still have to do things when I got up so late. In the daily three-way test, I found that the second one was hand tearing heap sorting. It's too ashamed. The original data structure was super confident. I wrote it from scratch for a long time this time, sobbing

Just finished the topic AC, which means that this article ends our heap sorting. Seriously sort out the heap sorting. After writing later, we have to supplement the non recursive traversal of the pre order, middle order and post order of the binary tree

By the way, when EDG plays DK tonight, I actually want to finish heap sorting + binary tree traversal in the afternoon and look at the results of B and B + trees in the evening. Forget it, things still have to be done one by one. Let's start
I just realized that I only knew how to build a heap before, but I didn't know how to sort the heap. That's what I just learned --

Heap introduction

In this part, let's talk about the concept. The establishment of the minimum heap and the maximum heap is the same truth. Below, we take the minimum heap as an example

In heap sorting, instead of rebuilding an array binary tree, we can maintain a heap on the original array. Our heap can be similar to a complete binary tree, but its nature is not similar to our binary search tree. The left and right sides are smaller than our nodes, and the other side is greater than No

The following figure is not Heapify stacked. I also marked it with serial number. Looking at the figure is actually an array. If we subtract 1 from the black, it will be the array subscript above


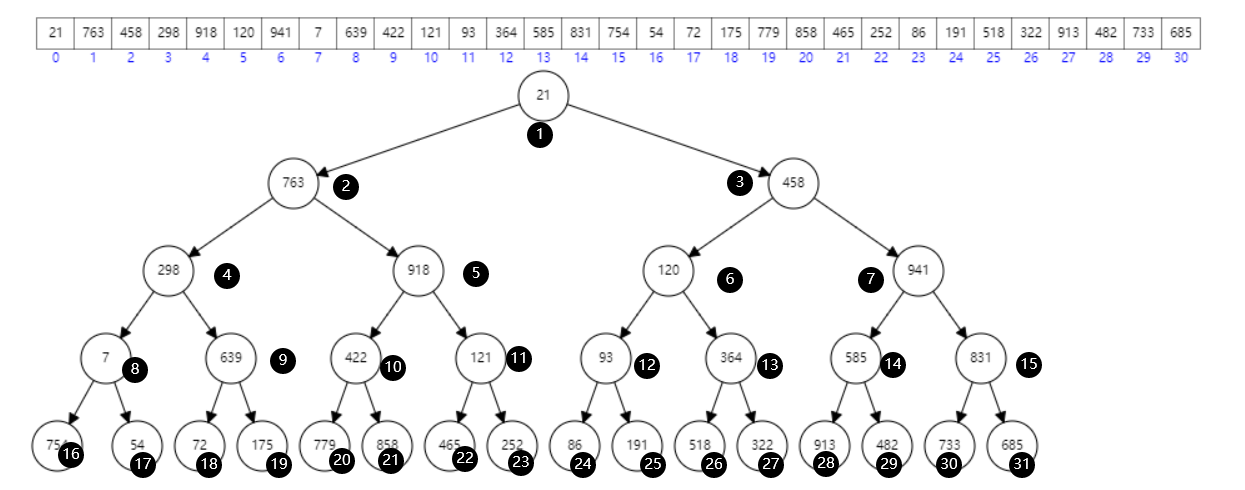
The following is the minimum heap. Let's take a closer look according to the following figure. After observation, we will directly enter the part of AdjustHeap

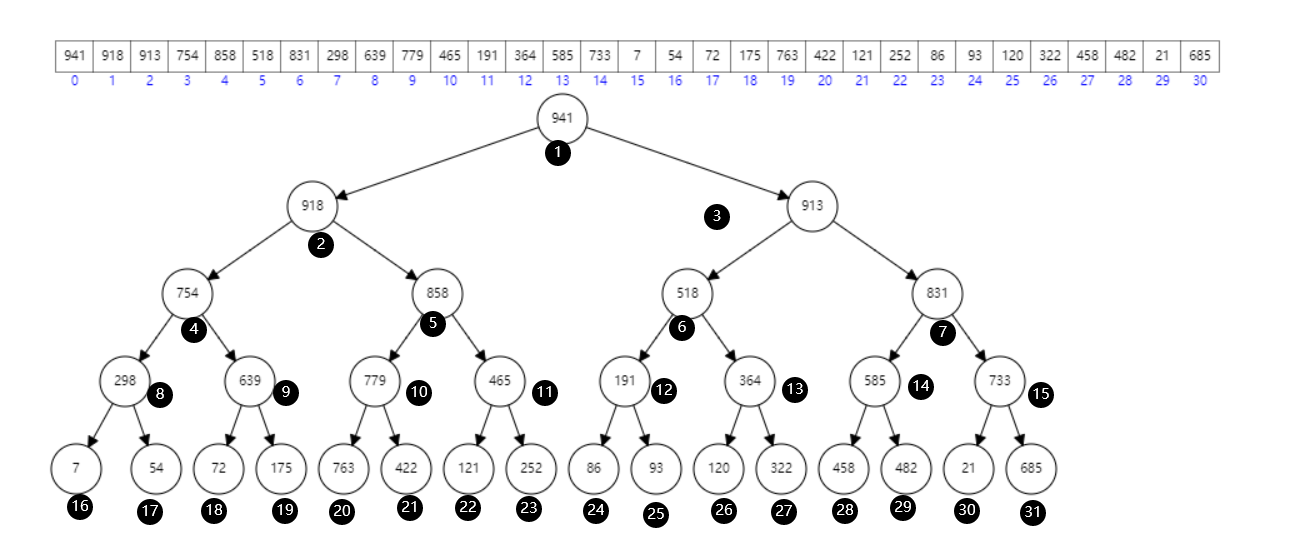
1. heapify (rebuild heap)

Haha, the first time I saw the name of this function was heapify. I wanted to use it, but I thought that the deletion operation also needs this function, so I changed it to adjustheap. I think it's more appropriate. Let's go on

In fact, our heap binary tree requirements are not high. What we need is that any of our parent nodes requires its adjacent child nodes. If it is the smallest heap, the parent node is required to be smaller than their two child nodes
As shown in the figure below, it has been pasted above. You can carefully observe that this is indeed the case

How can we complete such adjustment? I believe you have seen the video and should have some ideas. Next, you need to remind that if the subscript of the array starts with 0, the first non leaf node is (n-1)/2) and if the subscript starts with 1, it is n/2. In fact, you don't need to start the non leaf node at the beginning of the adjustment heap, but the useless adjustment time costs more

The following code is the code to initialize the heap. If there is no array initialization at the beginning, we fill in numbers one by one. The inserted data will be written later

class minheap
{
public:
    vector<int> heap;
    minheap() {heap.clear();}
	minheap(vector<int>& v)
	{ 
	    heap = v; //Initialize heap array
	    for(int i = (heap.size() - 1) / 2;i >= 0;--i)
	        adjustheap(heap,i); //Heap starts with non leaf nodes
	}
	
	void adjustheap(vector<int>& heap,int pos)
	{
	    if(heap.empty() || pos == heap.size()-1) //The heap is empty or has reached the leaf node
	        return;
	
	    int val = heap[pos];  //Initial node value
	    int maxpos = heap.size() - 1; //Maximum subscript of heap to prevent out of bounds
	    for(int i = pos*2+1;i <= maxpos;i = pos*2+1) //Next level node
	    {
	        //Compare the left and right child nodes I < maxpos to prevent cross-border
	        if(i < maxpos && heap[i+1] < heap[i])   ++i; 
	        if(val <= heap[i])  break; //If the conditions have been met, exit the adjustment
	
	        heap[pos] = heap[i];       // Assign the value of the lower sub node to the current position
	        pos = i;				   // Continue to adjust the downward iteration until it cannot be adjusted or the conditions are met
	    }
	    heap[pos] = val;              // Put our original value in the heap, that is, assign it to a suitable position
	}
};

2. push (insert data)

This part is simpler than the previous one. Let's look at the code directly

In this part, we insert the data directly into the tail of the array, and then start floating. If it cannot float up, it means that it has found its own position, then stop floating up and end the insertion

void push(int val)
{
    int pos = heap.size();
    heap.emplace_back(val);
    for(;val < heap[(pos - 1)/2];pos = (pos - 1)/2)
    {
        heap[pos] = heap[(pos - 1) / 2]; // If it is smaller than the previous one, it floats up
        if(pos == 0)    break; //Note that when pos is finally equal to 0, it will enter an endless loop. We must set this condition to exit
    }
    heap[pos] = val;
}

3. pop (delete data)

The idea of Pop is that we directly place the last bit of data in the header and then call our adjustheap to let it find its own location, because the tail of our array has found its own location again, and the tail of the last pop array can see the code.

int pop()
{
    int ret = heap[0]; //Return value saved in advance
    heap[0] = heap.back(); //The last bit directly covers the head, because our head will eventually return, which is about equal to pop
    heap.pop_back();
    adjustheap(heap,0); //Let it adjust to its own position
    return ret;
}

Minimum heap code implementation

Let's look at the code directly. This code is also Leetcode 912. The answer to sorting array is a sorting array. The code is as follows

class Solution {
public:
    class minheap
    {
    public:
        vector<int> heap;
        minheap() {heap.clear();}
        minheap(vector<int>& v)
        { 
            heap = v;
            for(int i = (heap.size() - 1) / 2;i >= 0;--i)
                adjustheap(heap,i);
        }

        void adjustheap(vector<int>& heap,int pos)
        {
            if(heap.empty() || pos == heap.size()-1)
                return;

            int val = heap[pos];
            int maxpos = heap.size() - 1;
            for(int i = pos*2+1;i <= maxpos;i = pos*2+1)
            {
                if(i < maxpos && heap[i+1] < heap[i])   ++i;
                if(val <= heap[i])  break;

                heap[pos] = heap[i];
                pos = i;
            }
            heap[pos] = val;
        }

        void push(int val)
        {
            int pos = heap.size();
            heap.emplace_back(val);
            for(;val < heap[(pos - 1)/2];pos = (pos - 1)/2)
            {
                heap[pos] = heap[(pos - 1) / 2];
                if(pos == 0)    break;
            }
            heap[pos] = val;
        }

        int pop()
        {
            int ret = heap[0];
            heap[0] = heap.back();
            heap.pop_back();
            adjustheap(heap,0);
            return ret;
        }

        bool empty()
        {
            return !heap.size();
        }

    };

    vector<int> sortArray(vector<int>& nums) {
        minheap heap(nums);
        vector<int> ret;

        while(!heap.empty())
            ret.emplace_back(heap.pop());
        return ret;
    }
};

Minimum heap example link

The following link is Leetcode 912. Sorting array link. You can verify whether there is a problem with your implementation. This blog will be written here first
912. Sort array
Love 6 brush record blog Leetcode 912. Sort array