preface
This chapter describes in detail the use and related operations of linked list, a linear data structure.
In fact, many people can't understand the link between the nodes and the link before the nodes. It will be very difficult to learn, because I was like this at the beginning. I figured it out later. In fact, it is the following idea:
For example, "temp.next", which sometimes represents a node and sometimes a pointer, is easy to understand as long as the concept is distinguished and brought into the code for understanding.
Single linked list
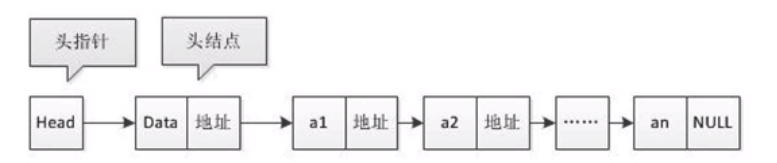
As shown in the figure, the linked list is connected by one node after another, and each node has a data field and a pointer field.
The data field is the data of this node, and the pointer field points to the address space of the next node.
This one needs xdm a little bit of foundation. If you really can't understand it, just look at the code and find more things to learn. It's over and you'll get on the road slowly. I directly give the implementation method here. You can find relevant videos or books to learn, because I feel that I use words to link the list, which is certainly not as clear as others use videos, and the comments in my code are very complete, which can be referred to and should be well understood.
Code implementation:
package Linked list;
public class LinkedListTest {
public static void main(String[] args) {
//test
//Create node
Node n1 = new Node(5);
Node n2 = new Node(4);
Node n3 = new Node(10);
Node n4 = new Node(6);
//Create single linked list
singleLinkedList list = new singleLinkedList();
//Add node
list.add(n1);
list.add(n2);
list.add(n3);
list.add(n4);
//Print single linked list
list.show(); //Output 5 4 10 6
//Delete function test: we delete 5
list.delete(5); //Output 4 10 6
list.show();
//Insert function test, we insert 88 after 4,
//The subscript here has the same meaning as the subscript value of the array
//That is, the parameters passed in should be index=1 and newNode.data=88
Node n5 = new Node(88);
list.insert(1,n5);
list.show(); //Output 4 88 10 6
//Test the update function. We update 88 to 99
list.update(88,99);
list.show(); //Output 4 99 10 6
}
}
//Define single linked list
class singleLinkedList{
//Initialize a head node. The head node does not move because it is the head of the whole linked list and does not store data
Node headNode = new Node(0);
//Return header method
public Node getHeadNode(){
return headNode;
}
//--------------------------------------------------------------------
//Method to add a new node to a single linked list: add
//Thinking, when the order is not considered
//1. Find the last node of the current linked list
//2. Mount the node to be added on the last node
//That is, let the pointer field of the last node point to the new node
public void add(Node newNode){
//First, create a working pointer to traverse the head node instead of the head node, so as not to change the position of the head node
//Because if the header pointer is used to traverse, the original address of the header pointer will change
Node temp = headNode;
while (true){
if(temp.next == null) break; //When temp traverses a node and the next field is null, it indicates that the tail node is reached
//If the tail node is not reached, the pointer moves back and continues to traverse the next node
temp = temp.next;
}
//When exiting the loop, it is proved that we have reached the last node and hang up our new node
temp.next = newNode;
}
//--------------------------------------------------------------------
//Method of inserting new nodes into single linked list: insert
//Idea:
//1. Use a counter cnt to calculate the number of positions traversed
//2. Start traversing from the first node, and insert a new node newNode when cnt = = the location index we want to insert
public void insert(int index,Node newNode){
Node temp = headNode; //Working pointer
int cnt = 0; //Counter
while(true){
if(temp.next == null) break; //After traversal, exit the loop
if(cnt == index){ //Find the target location and insert it
newNode.next = temp.next;
temp.next = newNode;
break;
}
temp = temp.next; //Pointer backward
cnt++;
}
}
//--------------------------------------------------------------------
//Method for deleting a node in a single linked list: delete
public void delete(int target){ //target: element to delete
Node temp = headNode;
while (true){
//To prevent null pointer exceptions, the judgment that the value ends when it is null should be placed on the first line
if(temp.next == null) break;
if(temp.next.data == target){ //Find the previous node of the node to be deleted before we can delete the node
temp.next = temp.next.next;
break;
}
temp = temp.next; //Pointer backward
}
}
//--------------------------------------------------------------------
//Method for updating a node in a single linked list: update
//srcData: the target element value in the linked list to be updated, and newData: the element value to replace
public void update(int srcData,int newData){
Node temp = headNode;
while (true){
if(temp.next == null) break; //After traversal, exit the loop
if(temp.data == srcData){ //If the target element value is found
temp.data = newData; //Replace data field with
break;
}
temp = temp.next; //Pointer backward
}
}
//--------------------------------------------------------------------
//How to traverse the output linked list: show
public void show(){
System.out.print("The single linked list data is:");
Node temp = headNode;
while (true){
if(temp.next == null) break;
temp = temp.next;
System.out.print(temp.data+" ");
}
System.out.println();
}
}
//Define node
class Node{
public int data; //Data domain
//Pointer field, pointing to the position of the next Node, because the next Node is also of Node type
//Therefore, the data type of this next is also Node
public Node next;
//The data field of the node is directly declared in the construction method
public Node(int data){
this.data = data;
}
//Print node information
@Override
public String toString() {
return "Node{" +
"data=" + data +
'}';
}
}
Linked list implementation stack data structure
The data structure of stack has been mentioned in the chapter of array. It will not be repeated here. It will be directly applied to the source code:
Code implementation:
package Linked list;
public class LinkedStack {
public static void main(String[] args) {
//test
//Create node
Node n1 = new Node(5);
Node n2 = new Node(4);
Node n3 = new Node(10);
Node n4 = new Node(6);
//Create stack
linkedListStack stack = new linkedListStack();
//Test stack function
stack.push(n1);
stack.show(); //Output 5
stack.push(n2);
stack.push(n3);
stack.push(n4);
stack.show(); //Output 5 4 10 6
//Test out stack function
stack.pop();
stack.show(); //Output 5 4 10
stack.pop();
stack.pop();
stack.show(); //Output 5
//Reentry stack
stack.push(n2);
stack.push(n3);
stack.show(); //Output 5 4 10
}
}
//Define stack
class linkedListStack {
//Define header node
Node headNode = new Node(0);
//Return header node
public Node getHeadNode() {
return headNode;
}
//--------------------------------------------------------
//Stack method push
public void push(Node newNode) {
//Working pointer
Node temp = headNode;
while (true) {
if (temp.next == null) break;
temp = temp.next;
}
temp.next = newNode;
}
//--------------------------------------------------------
//Stack out method pop
public int pop() {
Node temp = headNode;
while (true) {
if (temp.next.next == null) break;
temp = temp.next;
}
//When exiting the loop, temp is located at the penultimate node of the linked list
int element = temp.next.data; //Take out the value of the last node and return it later
//The last node pops up, that is, delete the last node
temp.next = null;
return element;
}
//--------------------------------------------------------
//Traversal stack
public void show(){
Node temp = headNode;
System.out.print("Stack data is:");
while (true){
if(temp.next == null) break;
temp = temp.next;
System.out.print(temp.data + " ");
}
System.out.println();
}
}
//Define node
class Node{
public int data; //Data domain
//Pointer field, pointing to the position of the next Node, because the next Node is also of Node type
//So this
public Node next;
//Directly declare a node in the constructor
public Node(int data){
this.data = data;
}
//Print node information
@Override
public String toString() {
return "Node{" +
"data=" + data +
'}';
}
}
The linked list implements the queue data structure
The queue is also introduced in the chapter of array, and the source code is given directly here.
Code implementation:
package Linked list;
public class LinkedListQueue {
public static void main(String[] args) {
//test
//Create node
Node n1 = new Node(5);
Node n2 = new Node(4);
Node n3 = new Node(10);
Node n4 = new Node(6);
//Create queue
LinkedQueue queue = new LinkedQueue();
//Test in queue
queue.put(n1);
queue.show(); //Output 5
queue.put(n2);
queue.put(n3);
queue.put(n4);
queue.show(); //Output 5 4 10 6
//Test out queue
queue.out();
queue.show(); //Output 4 10 6
queue.out();
queue.show(); //Output 10 6
}
}
class LinkedQueue{
//Define header node
Node headNode = new Node(0);
//Return header node
public Node getHeadNode(){ return headNode; }
//---------------------------------------------
//Queue
public void put(Node newNode){
Node temp = headNode;
while (true){
if(temp.next == null) break;
temp = temp.next;
}
temp.next = newNode;
}
//---------------------------------------------
//Out of queue
public int out(){
//The queue is one in and one out, because we added it at the end of the queue
//So we should go out of the queue at the head of the queue, so we can operate directly with the head node
//No working pointer is required
int element = headNode.next.data; //Take out the element of the team head and return later
headNode = headNode.next;
return element;
}
//---------------------------------------------
//Traversal queue
public void show(){
Node temp = headNode;
System.out.print("The queue data is:");
while (true){
if(temp.next == null) break;
temp = temp.next;
System.out.print(temp.data+" ");
}
System.out.println();
}
}
//Define node
class Node{
public int data; //Data domain
//Pointer field, pointing to the position of the next Node, because the next Node is also of Node type
//So this
public Node next;
//Directly declare a node in the constructor
public Node(int data){
this.data = data;
}
//Print node information
@Override
public String toString() {
return "Node{" +
"data=" + data +
'}';
}
}
Realize bidirectional linked list
Why is there a two-way linked list?
Because of the problems with the single linked list:
1. For one-way linked lists, the search direction can only be one direction, while two-way linked lists can search forward or backward.
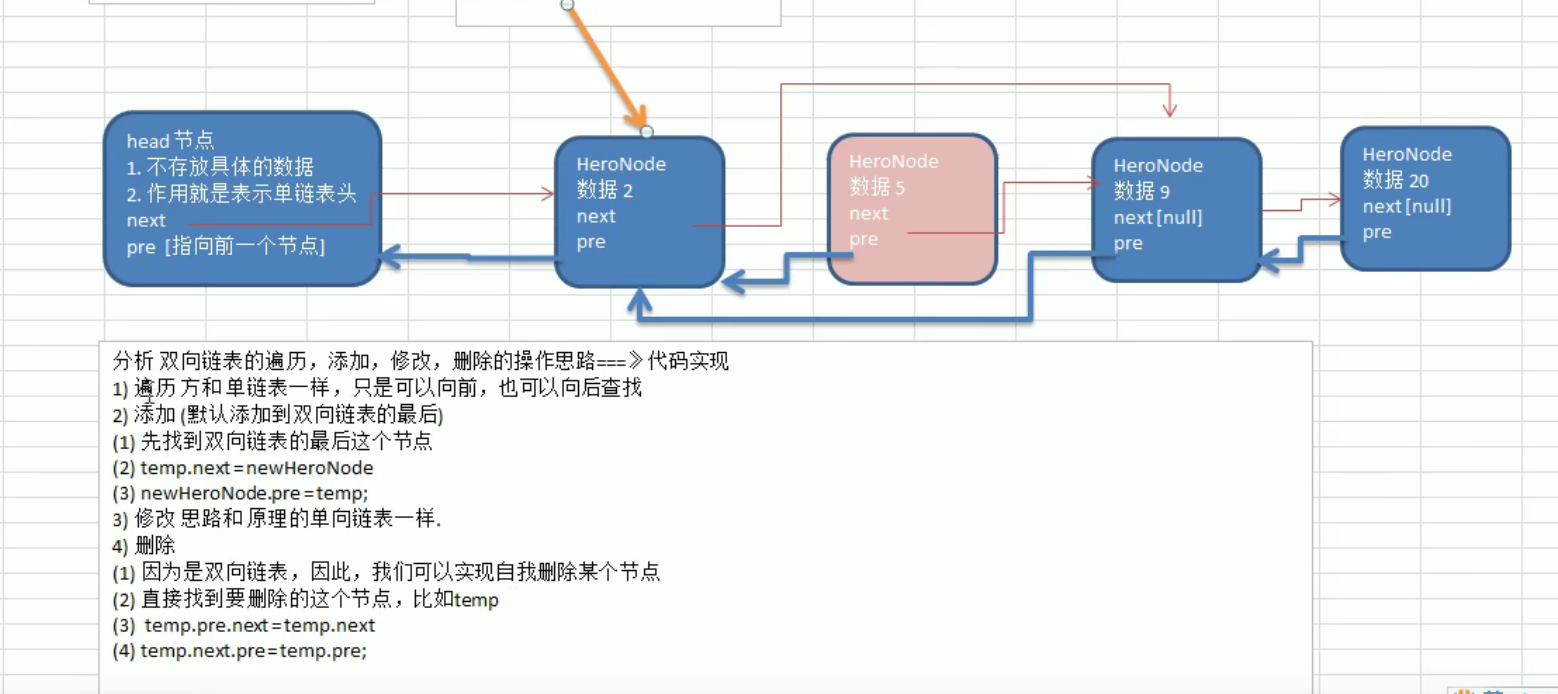
2. A one-way linked list cannot be deleted by itself. It needs to rely on auxiliary nodes, while a two-way linked list can be deleted by itself. Therefore, when deleting a node in the previous single linked list, we always find temp. Temp is the previous node of the node to be deleted. We use it to delete the node we want to delete.
In fact, the two-way linked list is not complicated, that is, it has one more precursor pointer pre than the original single linked list.
The idea of adding, deleting, modifying and querying a two-way linked list is as follows:
Code implementation:
package Linked list;
public class DoubleLinked {
public static void main(String[] args) {
//test
//Create node
Node n1 = new Node(5);
Node n2 = new Node(4);
Node n3 = new Node(10);
Node n4 = new Node(6);
//Create a two-way linked list
doubleLinkedList list = new doubleLinkedList();
//Add function test
list.add(n1);
list.show(); //Output 5
list.add(n2);
list.add(n3);
list.add(n4);
list.show(); //Output 5 4 10 6, 6 4 10 5
//Test of deletion function: we delete 5
list.delete(5);
list.show(); //Output 4 10 6, 6 4 10
//Test of update method: we update 4 to 88
list.update(4,88);
list.show();//Output 88 10 6, 6 10 88
//Test of insertion method: we insert 99 after 88, that is, insert 99 in the second position
//That is, index=2, newNode.data=99
Node n5 = new Node(99);
list.insert(2,n5);
list.show(); //Output 99 88 10 6, 6 10 88 99
}
}
//Define bidirectional linked list
class doubleLinkedList{
//Define header node
Node headNode = new Node(0);
//Return header node
public Node getHeadNode(){ return headNode; }
//-----------------------------------------------
//Add node
//Nothing special, just add it at the end by default
public void add(Node newNode){
Node temp = headNode;
while (true){
if(temp.next == null) break;
temp = temp.next;
}
temp.next = newNode;
newNode.pre = temp;
}
//-------------------------------------------------
//Delete delete
public void delete(int target){ //Target delete target value
Node temp = headNode;
boolean flag = false; //Flag whether the last node is deleted
//If the last node is deleted, we should change the operation
while (true){
if(temp.next == null) {
flag = true; //The last node is deleted
break;
}
if(temp.data == target){
//The precursor pointer of the next node of temp points to the previous node of temp node
temp.next.pre = temp.pre;
//The subsequent pointer of the previous node of temp points to the next node of temp node
temp.pre.next = temp.next;
break; //Exit loop
}
temp = temp.next; //Pointer backward
}
if(flag == true){
//Because the last node is deleted, and temp represents the last node
//Then we first set the subsequent pointer of the previous node of temp to null
temp.pre.next = null;
//Then set the precursor pointer of temp to null
temp.pre= null;
}
}
//---------------------------------------------
//insert elements: insert
//index: where to insert. newNode: insert a new node
public void insert(int index,Node newNode){
Node temp = headNode;
int cnt = 0; //Counter, which node position does the count traverse to
while (true){
if(temp == null) break;
if(cnt == index){ //Find insertion location
//The subsequent pointer of the previous node of temp points to the new node
temp.pre.next = newNode;
//The precursor pointer of the new node points to the previous node of temp
newNode.pre = temp.pre;
//The precursor pointer of temp points to the new node
temp.pre = newNode;
//The subsequent pointer of the new node points to temp
newNode.next = temp;
break;
}
temp = temp.next;
cnt++;
}
}
//---------------------------------------------
//Update method update
//srcData, target element to update, targetData: data element to replace
public void update(int srcData,int targetData){
Node temp = headNode;
while (true){
if(temp == null) break;
if(temp.data == srcData){
temp.data = targetData;
break;
}
temp = temp.next;
}
}
//---------------------------------------------
//Traversal queue
public void show(){
Node temp = headNode;
System.out.print("The backward traversal data is:");
while (true){
if(temp.next == null) break;
//The pointer moves successively and then outputs the value to avoid the data value in the header node
//Because our default header node does not put values
temp = temp.next;
System.out.print(temp.data+" ");
}
System.out.println();
System.out.print("The forward traversal data is:");
while (true){
if(temp.pre == null) break;
//This is also to avoid the data value in the header node
//It's written differently because it's traversed from back to front
System.out.print(temp.data+" ");
temp = temp.pre;
}
System.out.println();
}
}
//Define node
class Node{
public int data; //Data domain
public Node next; //next is a pointer to the following node
public Node pre; //pre is a pointer to the previous node
//Directly declare a node in the constructor
public Node(int data){
this.data = data;
}
//Print node information
@Override
public String toString() {
return "Node{" +
"data=" + data +
'}';
}
}
Ring linked list to solve Joseph Ring problem
Why is there a one-way circular linked list?
Look at the problem of losing handkerchiefs:

Logic diagram of ring linked list:

The circular linked list also involves the very classic Joseph Ring:

for instance:
Now there are five children (n = 5), and then start counting from the first person (i.e. k = 1). When the number is 2 (m = 2), the child will be out of the queue.
The schematic diagram is as follows:
At the beginning, there were five children. They were in the state of a circular linked list:

It can be seen from the meaning of the question that the first person starts counting, and the person whose check-in number is 2, that is, No. 2, leaves the queue. After deleting the node, the situation is as follows:

Then start counting from 3, because it is the first person behind No. 2 who has just left the queue, so node 2 is the fourth person, so he leaves the queue. The node is deleted, that is, the current order of leaving the queue is 2 - > 4. The following analysis logic is the same. It is worth noting that when there is only one node left at the end of deletion, it can also form a closed loop:

Implementation of one-way ring linked list:
Idea of creating circular linked list:
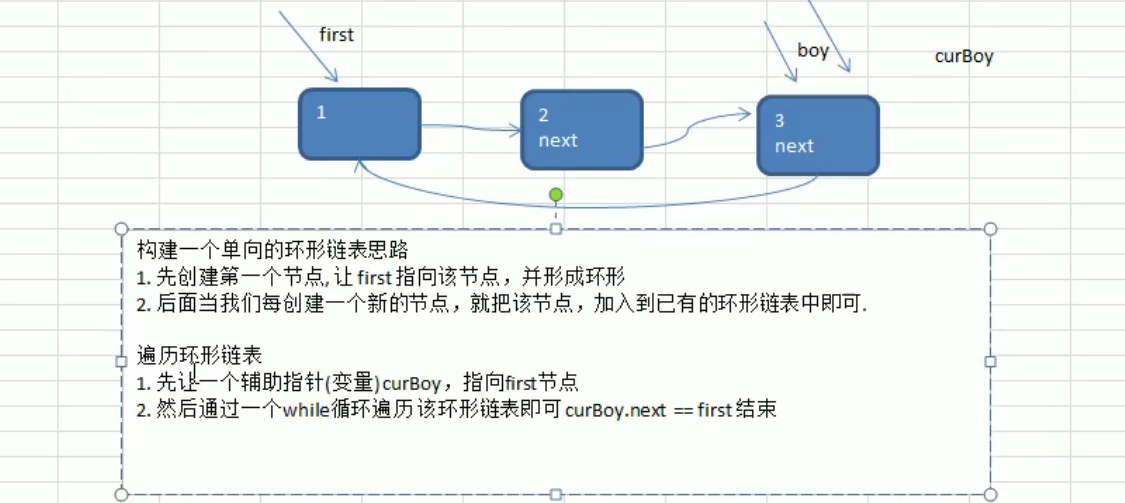
Idea of out of queue sequence method:
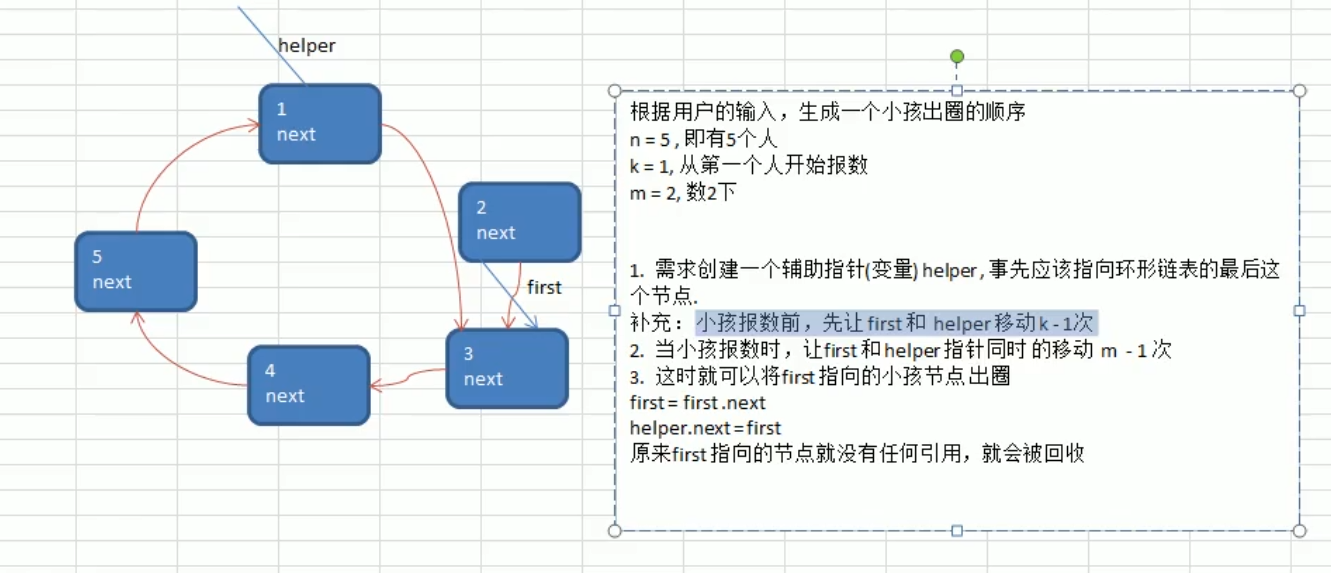
There are three pointer variables. One is first, which points to the first node (i.e. the first person) of the current ring linked list. It will not change and always points to the first person. Then there are two pointers, boy and curBoy. Where curBoy is an auxiliary pointer, pointing to our current boy node (currentBoy), which is used to help build our ring linked list. The boy pointer represents each of our boy nodes. There are detailed comments in the code. Some abstractions are described here.
package Linked list;
public class Josepfu {
public static void main(String[] args) {
//test
//Create circular linked list
CircleSingleLinkedList list = new CircleSingleLinkedList();
//We created a circular linked list with five children
list.addBoy(5);
//Test traversal function
list.showBoy(); //Output 1,2,3,4,5
//Now let's test the circle order
list.countBoy(1,2,5);//Output 2,4,1,5,3
}
}
//Create circular linked list
class CircleSingleLinkedList{
//Create a new first node to represent the first Boy node. You can have no value first, because we are not sure about the number
public Boy first = null;
//-------------------------------------------------------------
//We provide an addBoy method to receive the number of nodes in the ring
//Then create the corresponding ring linked list
public void addBoy(int n){
Boy curBoy = null; //Auxiliary pointer, used to help build a ring linked list
//Use the for loop to create a circular linked list
for (int i = 1; i <= n; i++) {
//According to the number, a boy node is created every cycle
Boy boy = new Boy(i);
if(i == 1){ //It means meeting the first child
//Then we point the first pointer to it, and the first will not move after that
first = boy;
first.next = first; //Point to yourself and form a ring
curBoy = first; //Let curBoy point to the first child
}else{ //This indicates that it is not the first boy node
//curBoy points to the first node. The following sentence points the next field of the first node to the new boy node
curBoy.next = boy;
//The next field of the new boy node should point to the head node first to form a loop
boy.next = first;
//Our auxiliary pointer should also point to the second node, not to the first node
curBoy = boy;
//The following nodes 2, 3, 4... Are added with this logic
}
}
}
//--------------------------------------------------------
//Traverse the current circular linked list
public void showBoy(){
//Determine whether the linked list is empty
if(first == null) {
System.out.println("No children, Ow");
return;
}
//Because the first header pointer cannot move, we still use an auxiliary pointer for traversal
Boy curBoy = first;
while (true){
System.out.printf("The child's number is %d \n",curBoy.no);
if(curBoy.next == first) { //It indicates that the traversal has reached the head again. The traversal is over
break;
}
curBoy = curBoy.next; //curBoy pointer moves back
}
}
//-------------------------------------------------------
//According to the user's input, calculate the order of the child's circle
//startNo: indicates the number of children to start counting
//countNum: indicates how many times to count
//Num: indicates how many children are in the circle
public void countBoy(int startNo,int countNum,int nums){
//First, create an auxiliary traversal helper
Boy helper = first;
//Make it point to the last node in the linked list
while (true){
if(helper.next == first) break; //Traverse to the last node and exit the loop
helper = helper.next;
}
//Before the child counts off, let the first and helper move startNo-1 times, minus once because they only need to move once between two points
//It means to make these two pointers ready before moving, because the first point must be the first child to count first
//Pay attention to drawing and understanding, otherwise it will be a little abstract
for (int i = 0; i < startNo-1; i++) {
first = first.next;
helper = helper.next;
}
//Loop out of the loop until there is only one node left in the last loop
while (true){
if(helper == first) break; //If there is only the last node in the circle, exit the loop
//When the child counts off, let the helper and first pointer move countNum-1 times at the same time
//That is, how many times to report and move
for (int i = 0; i < countNum-1; i++) {
first = first.next;
helper = helper.next;
}
//After the move, it indicates that the counting is completed, and the boy node pointed to by first is circled
System.out.printf("No %d Children out of the circle \n",first.no);
//At this time, point first to its next node and make the node to which first currently points out of the circle
first = first.next;
helper.next = first;
//If the node pointed to by the original first does not have any reference, it will be recycled by GC
}
//Now, you can complete all the operations by turning the last child out of the circle
System.out.printf("The number of the last child out of the circle is:%d \n",first.no);
}
}
//Create a Boy class to represent a node
class Boy{
public int no; //Number, which can be understood as data field
public Boy next; //Pointer field, pointing to the next node
//When constructing a new Boy instance, assign the value of the data field to the node
public Boy(int no){
this.no = no;
}
//Print node information
@Override
public String toString() {
return "Boy{" +
"no=" + no +
'}';
}
}