1, Problem description

Problem Description: the n queen problem studies how to place n queens in n × N's chessboard, and the Queens can't attack each other. Give you an integer n and return the solution of all different N Queen problems. Each solution contains a different chess placement scheme for the n-queen problem, in which 'Q' and '.' represent the queen and the vacancy respectively. Queens cannot attack each other, that is, no two Queens can be in the same horizontal, vertical or diagonal line.
The following is the result model of the 4 queen problem:

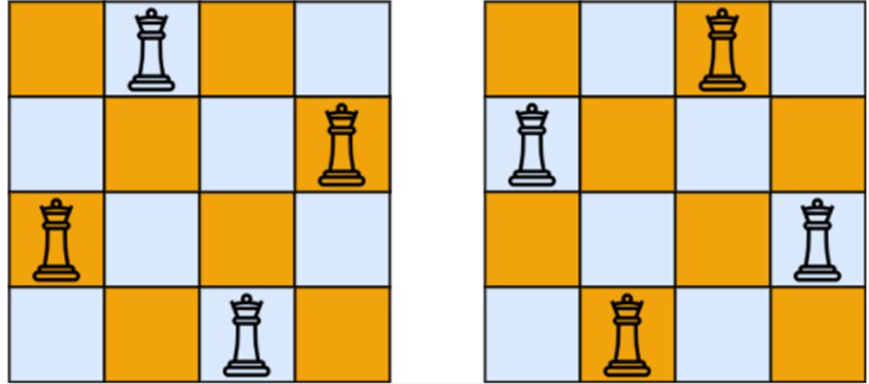
Input: n = 4
Output: [". Q...,"... Q "," q..., "... Q.], ["... Q. "," q..., "... Q",".Q...]]
Explanation: 4 there are two different solutions to the queen problem

Input: n = 1
Output: ["Q"]]
Explanation: 1. There is only one solution to the queen problem

2, Problem analysis

This problem requires putting n queens in one n × N on the chessboard, so that any two Queens can't go together, can't be in the same column, and can't be on the same diagonal. Solve it with the idea of backtracking: because each queen must occupy a row, our problem is to assign an appropriate column to the queen of each row.
When n=1,2,3, the problem is very simple, so we start with n=4. The solution process is as follows:
The figure below shows an empty chessboard model of 4 queens problem,

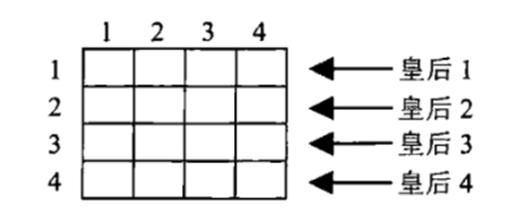
We start with an empty chessboard. First, put queen 1 in the first possible position of its row (the first column at this time), that is, the coordinates of Queen 1 are (1,1); For Queen 2, try to fill it in the first column to check whether it meets the rules. If it fails, the second column also fails, and the third column meets the requirements, that is, Queen 2 is filled in (2,3); Then find the first possible position of queen 3 according to the rules, but it is found that none of the four positions match, so backtrack the algorithm, put queen 2 on the next possible position, that is, (2, 4), so that queen 3 can be placed on (3,2), find out whether queen 4 can be placed, and then find the position that does not match, and then backtrack to queen 3. Queen 3 has no position to try again, There is no place to try back to Queen 2. Go back to Queen 1, put queen 1 on (1,2), then follow the same steps to put queen 2 on (2,4), queen 3 on (3,1), and queen 4 on (4,3). This is a solution when n=4, and then go back again to find the remaining solutions.

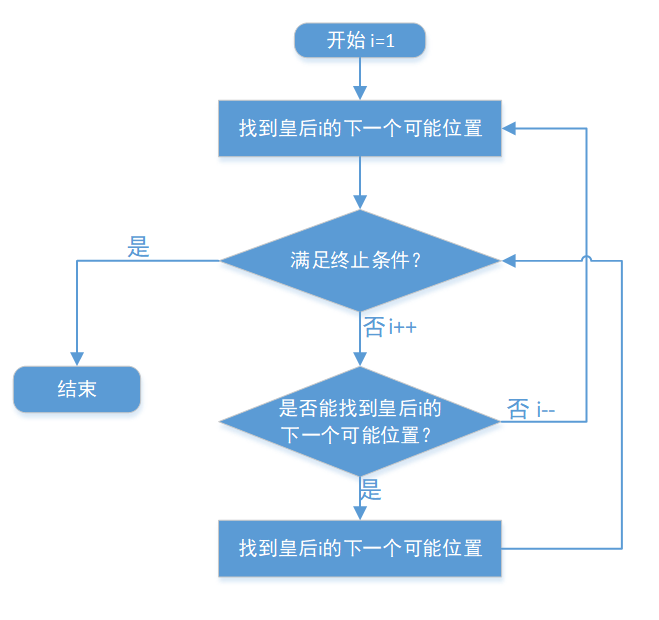
3, Algorithm flow chart

4, Source code

class Solution {
    List<List<String>> res = new ArrayList<>();
    public List<List<String>> solveNQueens(int n) {
        char[][] chessboard = new char[n][n];
        for (char[] c : chessboard) {
            Arrays.fill(c, '.');
        }
        backTrack(n, 0, chessboard);
        return res;
    }

    public void backTrack(int n, int row, char[][] chessboard) {
        if (row == n) {
            res.add(Array2List(chessboard));
            return;
        }
        for (int col = 0;col < n; ++col) {
            if (isValid (row, col, n, chessboard)) {
                chessboard[row][col] = 'Q';
                backTrack(n, row+1, chessboard);
                chessboard[row][col] = '.';
            }
        }
    }

    public List Array2List(char[][] chessboard) {
        List<String> list = new ArrayList<>();
        for (char[] c : chessboard) {
            list.add(String.copyValueOf(c));
        }
        return list;
    }

    public boolean isValid(int row, int col, int n, char[][] chessboard) {
        // Check column
        for (int i=0; i<row; ++i) { // Equivalent to pruning
            if (chessboard[i][col] == 'Q') {
                return false;
            }
        }

        // Check the 45 degree diagonal
        for (int i=row-1, j=col-1; i>=0 && j>=0; i--, j--) {
            if (chessboard[i][j] == 'Q') {
                return false;
            }
        }

        // Check the 135 degree diagonal
        for (int i=row-1, j=col+1; i>=0 && j<=n-1; i--, j++) {
            if (chessboard[i][j] == 'Q') {
                return false;
            }
        }
        return true;
    }
}

5, Complexity

The time complexity is: O(N!)
Analysis: use an array to record the column subscript of the queen placed in each row, and place a queen in each row in turn. Every time a newly placed queen cannot attack an already placed Queen: that is, the newly placed queen cannot be in the same column and on the same slash as any already placed queen, and update the queen column subscript of the current row in the array. When N queens are placed, a possible solution is found. When a possible solution is found, the array is converted into a list representing the chessboard state, and the list of the chessboard state is added to the return list.
Since each queen must be in a different column, no other queen can be placed in the column where the queen has been placed. The first queen has N columns to choose from, the second queen has at most N − 1 columns to choose from, and the third queen has at most N-2 columns to choose from (if considering that it cannot be on the same slash, the number of possible choices is less), so all possible situations will not exceed N! The time complexity of traversing these cases is O(N!).