
🍉 Linear table
A linear list is a finite sequence of n data elements with the same characteristics. Linear table is a data structure widely used in practice. Common linear tables: sequential table, linked list, stack, queue, string
A linear table is logically a linear structure, that is, a continuous straight line. However, the physical structure is not necessarily continuous. When the linear table is stored physically, it is usually stored in the form of array and chain structure.

🍉 Sequence table
Sequential table is a linear structure in which data elements are stored in sequence with a storage unit with continuous physical addresses. Generally, array storage is used. Complete the addition, deletion, query and modification of data on the array.
🌵 Concept and structure of sequence table
The sequence table can generally be divided into:
Static sequential table: use fixed length array storage.
Dynamic sequential table: use dynamic array storage.
Static sequence table is suitable for determining the scene where you know how much data you need to save
The fixed length array of static sequence table leads to large N, waste of space and insufficient space
In contrast, dynamic sequential tables are more flexible and dynamically allocate space as needed
Next, the implementation of dynamic sequence table is explained in detail
🍌 Implementation of sequence table interface (comments are very detailed, I 👴👴 Can understand)
First write the member properties and constructors of this sequence table class

Then, implement the next interfaces
🍈 Print sequence table
It's very simple here. Just like traversing an array, you can traverse the sequence table once
// Print sequence table
public void display() {
for (int i = 0; i < this.usedSize; i++) {//Traverse and print valid elements
System.out.print(this.elem[i]+" ");
}
System.out.println();
}
🍈 Add new element in pos position
The idea here is divided into the following steps:
- ① Judge whether pos is legal
- ② Judge whether the sequence table is full or not (an additional judgment method isFull() needs to be written here). If it is full, the capacity of Arrays.copyOf() needs to be expanded
- ③ The elements after pos move back one position in turn
- ④ Put the target element data into this pos position
//Determine whether the sequence table is full
public boolean isFull() {//The judgment method is to compare the number of effective elements with the length of the array
if (usedSize==elem.length)//If the two are equal, the array is full
return true;
else
return false;
}
// Add new element in pos position
public void add(int pos, int data) {
if (pos>=0 && pos<=usedSize){ //First, make sure pos is legal
if (isFull()){//Determine whether the capacity is full
this.elem = Arrays.copyOf(this.elem,this.elem.length+1);//Full capacity expansion
}
for (int i = usedSize-1 ; i >= pos ; i--){
//To move from back to front, not from back to back, so that the value of the previous position moves to the value of the next position,
//Then the value in the latter position will be overwritten, resulting in all the values behind becoming the same as the first moving value
elem[i+1] = elem[i];//Move 1 bit backward from all elements after the new element position
}
this.elem[pos] = data;//Insert data into pos location
this.usedSize++;//Effective element + 1
}
else
System.out.println("Illegal location");
}
🍈 Get sequence table length
This is very simple. Just get the effective length useSize of the member property
// Gets the valid data length of the sequence table
public int size() {
return this.usedSize;
}
🍈 Determine whether an element is included
Pass in the elements to be found, and then find them in turn among all valid elements
// Determines whether an element is included
public boolean contains(int toFind) {
for (int i =0 ; i<usedSize ; i++){//Find the valid elements in turn
if (elem[i]==toFind)
return true;
}
return false;
}
🍈 Find the location of an element
Here you can use traversal of valid elements. As above, I just want to review binary search, because binary search is also a kind of traversal, but it can improve the efficiency of traversal
// Find the corresponding position of an element (review the binary search)
public int search(int toFind) {
int left = 0; //Set a left subscript
int right = elem.length-1;//Set another right subscript, and the value is array length - 1
while (left <= right) {//Circular search, the condition is left subscript < = right subscript
//=Don't forget the number, or you will miss a case (where the checked value is the last element)
int mid=(left+right)/2;//Set an intermediate value to halve the elements to be traversed to improve efficiency
if (elem[mid]<toFind){//If the intermediate value is less than the target value, the next element of the intermediate value is set as the left value
left = mid+1;
}//Same as above
else if (elem[mid]>toFind){
right = mid-1;
}
else//If the intermediate value is neither greater than nor less than the target value, then the intermediate value is the target value to find, and just return its subscript
return mid;
}
System.out.println("There is no such number");
return -1;
}
🍈 Gets the element of the pos location
If you pass in a location, first judge whether the location is legal. If it is legal, just return the elements in the location directly
// Gets the element of the pos location
public int getPos(int pos) {
if (pos>=0 && pos<=usedSize)//Judge whether the location is legal
return elem[pos];
else
return -1;//If the location is illegal, return - 1 to indicate that the location is illegal
}
🍈 Set the element of pos position to value
Still, first judge whether the location is legal. If it is legal, directly assign value to this location to overwrite the original data
// Set the element of pos position to value
public void setPos(int pos, int value) {//Pass in the location and the value you want to assign
if (pos>=0 && pos<=usedSize){//Judge whether it is legal
elem[pos]=value;
}
else
System.out.println("pos illegal");
}
🍈 Delete the first occurrence of data
First call the search interface written above to determine whether there is this data. If so, start from this data and successively overwrite the next data of the current data with the current data to realize the deletion function. Don't forget the effective element - 1
//Delete the keyword key that appears for the first time
public void remove(int toRemove) {
if (-1==this.search(toRemove)){
System.out.println("There is no such element");
}
else{
int index = this.search(toRemove);//Get the location of the data to delete (subscript)
for (int i = index ; i<usedSize-1 ; i++)//Starting from this data, the next data of the current data will be overwritten with the current data to realize the deletion function
elem[i]=elem[i+1];
usedSize--;//Note that after deleting an element, the valid elements of the whole sequence table should also be - 1
}
}
🍈 Empty sequence table
Here we use the most brutal method to directly clear the number of effective elements. In fact, it doesn't matter whether the array elements become 0 or not, because new data will be overwritten the next time we use it
// Empty sequence table
public void clear() {
this.usedSize = 0;
}
🍌 Defects of sequence table
- 1. Insert and delete the middle / header of the sequence table, with a time complexity of O(N)
- 2. Capacity increase requires applying for new space, copying data and releasing old space. There will be a lot of consumption.
- 3. The capacity increase is generally double, which is bound to waste some space. For example, if the current capacity is 100 and the capacity is increased to 200 when it is full, we continue to insert 5 data, and there is no data to insert later, then 95 data spaces are wasted.
Will the linked list have the above problems? Please look down 👇👇
🍉 Linked list
🌵 Concept and structure of linked list
Linked list is a discontinuous storage structure in physical storage structure. The logical order of data elements is realized through the reference link order in the linked list.
The linked list structure is very diverse. There are 8 linked list structures in the following cases:
- Unidirectional and bidirectional
- Take the lead, don't take the lead
- Cyclic and non cyclic
We focus on the following two linked lists
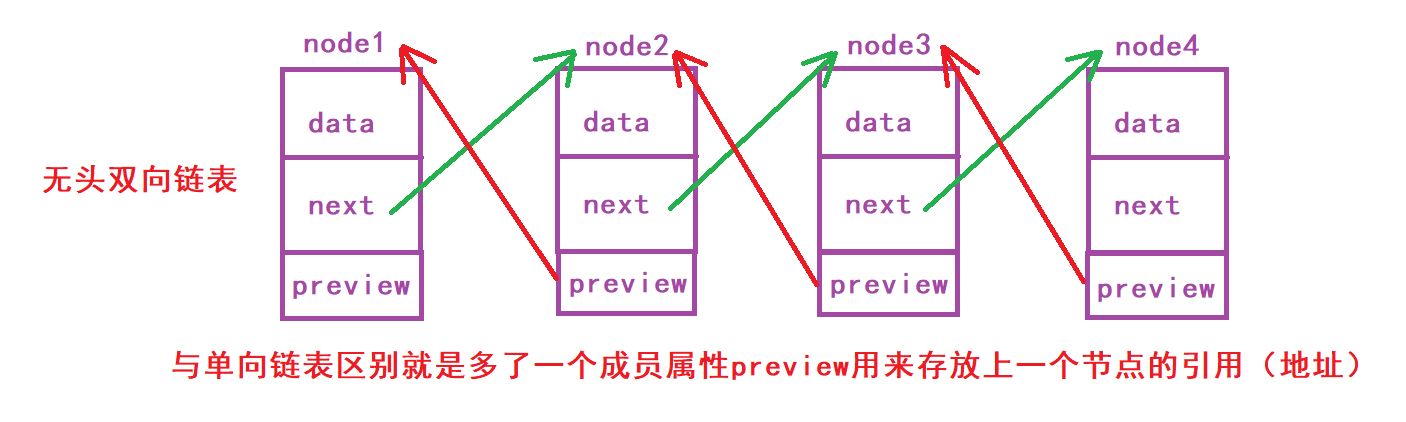
🍌 Implementation of headless one-way acyclic linked list interface (notes are very detailed, I 👴👴 Can understand)
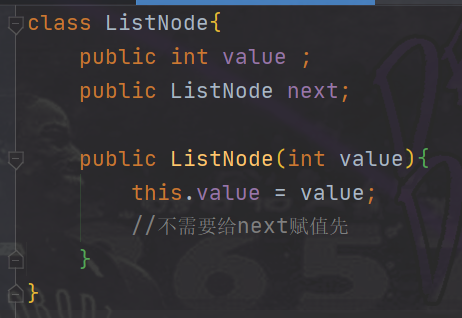
First write two classes, one is the linked list class (including a variable header node and interfaces to realize various functions. Because it is a headless linked list, the header node is variable), and the other is the node class (the member attributes are value and next)

The following interfaces are written in the linked list class. Because the linked list is an object, we want to realize all the functions of a linked list object
🍈 Print linked list
Printing a linked list is actually similar to printing a sequential list. It's good to traverse the linked list, but pay attention to one point. Here, you need to introduce a local variable cur to traverse instead of the head node, because the head node is fixed before adding or deleting nodes. Don't let the head node change
//Print linked list
public void display(){
ListNode cur = this.head;//Create a local variable cur instead of head, so that the head node will not change
while (cur!=null) {//The traversal condition is that the reference (address) of the next node is not null
System.out.print(cur.value+" ");
cur = cur.next;//Find next node
}
System.out.println();
}
🍈 Head insertion
As the name suggests, the header insertion method is to insert a node from the header to make the newly created node a new header node. Here, an additional point needs to be considered, that is, whether the header node exists (whether the linked list is empty), but the following code can deal with the case where the header node is empty (note that the address of the original head node should be stored in the new node first, and then the new node reference should be assigned to the original head node to become a new head node)
//Head insertion
public void addFirst(int data){
ListNode node = new ListNode(data);//Create a new node and initialize the data of the node
node.next = this.head;//Save the current header node address to the next of the new node
this.head = node;//Change the newly created node into a head node
//These two lines of code include the case that the header node is null
}
🍈 Tail insertion
The tail interpolation method is different from the head interpolation method. You must first judge whether the linked list is empty (judge whether the head node is null), and then introduce the local variable cur to traverse the linked list until cur.next is empty, indicating that the tail node is found. At this time, cur is the tail node
//Tail interpolation
public void addLast(int data){
//Find the tail. cur.next is null, indicating that this is the tail node
ListNode node = new ListNode(data);//Create a new node and initialize the data of the node
if (this.head == null){ //For the first time of tail interpolation, you must judge whether the head node is empty
this.head = node;//If it is the first insertion, the new node is the head node
}
ListNode cur = this.head; //The local variable cur is introduced to traverse the linked list
while(cur.next != null){ //If next equals null, it will jump out of while
cur = cur.next;//Find next node
}
cur.next = node;
}
🍈 Find out whether the keyword key is included in the single linked list
Pass in the keyword key and still introduce the local variable cur to traverse the linked list. The value of which node is equal to the key indicates that there is this keyword in the linked list. Return true, otherwise return false
//Find out whether the keyword is included and whether the key is in the single linked list
public boolean contains(int key){
ListNode cur = this.head;//Introduce local variable cur traversal
while(cur != null){//The loop condition is that the node reference is not null
if (key == cur.value)
return true;//If found, return true
cur = cur.next;//Find next node
}
return false;
}
🍈 Get the length of the single linked list
The local variable cur is still used to traverse the linked list, and an additional local variable size is set to count. As long as the node is not null, the size will be + 1. Finally, the returned value of size is the length of the linked list
//Get the length of the single linked list
public int size(){
int size=0;//Introduce local variables to count
ListNode cur = this.head;
while(cur != null){//Traverse and count
size++;//Node is not null, counter + 1
cur = cur.next;//Find next node
}
return size;//Return linked list length
}
🍈 Insert at any position, and the first data node is subscript 0
First, you have to judge whether the location you want to insert is legal. Then, you need to write an additional method findIndex() to find the node before the insertion location, which is used to insert the node and the insertion principle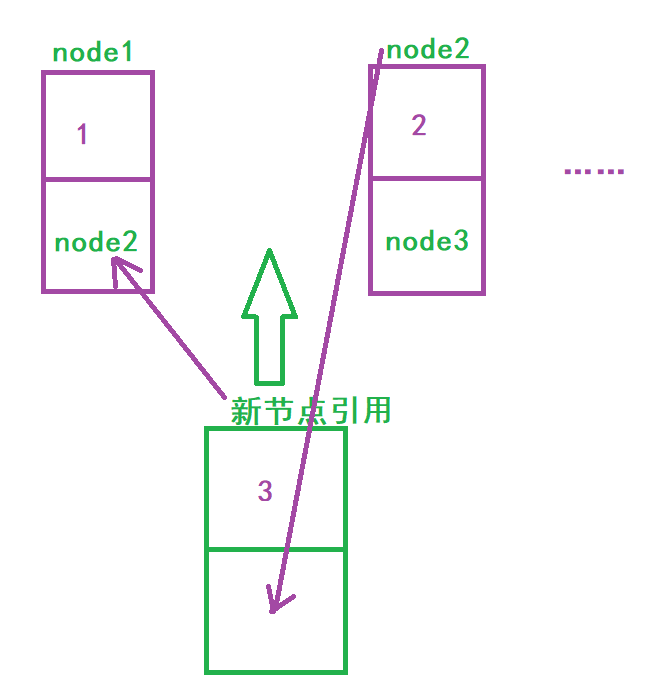
//Find the previous node according to the passed in index and return the address
public ListNode findIndex(int index){
ListNode cur = this.head;//Introduce local variables to traverse to the node before index
while (index-1 != 0){//The stop condition is that index-1 is equal to 0
//That is to say, it traverses to a node at the index position
cur = cur.next;//Backward traversal
index--;//index minus 1 for every backward node
}
return cur;//Returns the previous node reference of index
}
//Insert at any position, and the first data node is subscript 0
public void addIndex(int index,int data){//You need to create a function to find the node before the index position
if (index > 0 && index < size()) {//Determine whether the insertion position is legal
ListNode node = new ListNode(data);//Create a new node and initialize the data of the node
node.next = findIndex(index).next;//Assign the next node reference of the previous node in the index position to the next node of the newly inserted node through the search method written above
findIndex(index).next = node;//Save the reference of the new node to the next of the found node to achieve the link effect
}
else if (index==0) {//If the insertion position is 0, the head insertion method is used directly
addFirst(data);
return;
}
else if(index==size()) {//If the insertion position is the length value of the linked list, the tail insertion method is used directly
addLast(data);
return;
}
else
System.out.println("Illegal location!");
return;
}
🍈 Delete the node whose keyword is key for the first time
First, judge whether the head node is null (whether the linked list is empty), and then there are two cases
① Keyword in head node: set the next node of the head node as a new head node
② Keyword is not in the header node: assign the next node reference of the node with keyword to the next node of the previous node with keyword
//Delete the node whose keyword is key for the first time
public void remove(int key){
if (this.head == null){//Determine whether the linked list is empty
System.out.println("The linked list is empty and cannot be deleted");
return;
}
ListNode cur = this.head;
while(cur.next != null){//Traversal linked list
if(cur.value == key) {//① Keyword in head node: set the next node of the head node as a new head node
head = cur.next;
return;
}
else if(cur.next.value == key) {//② Keyword is not in the header node: assign the next node reference of the node with keyword to the next node of the previous node with keyword
cur.next = cur.next.next;
return;
}
cur = cur.next;
}
System.out.println("There are no nodes you want to delete");
}
🍈 Delete all nodes with the value of key
It is similar to deleting the key for the first time, except that return is changed to continue. In addition, a local variable size needs to be set. After the deletion process, if the size value set before deletion does not change, it means that the node has not been deleted
//Delete all nodes with the value of key
public void removeAllKey(int key){
int size = size();
if (this.head == null){
System.out.println("The linked list is empty and cannot be deleted");
return;
}
ListNode cur = this.head;
while(cur.next != null){
if(cur.value == key) {
head = cur.next;
continue;//Don't return after deletion. Continue to traverse
}
else if(cur.next.value == key) {
cur.next = cur.next.next;
continue;//Don't return after deletion. Continue to traverse
}
cur = cur.next;
}
if(size()==size) {//If the size set before deletion is equal to the value returned by the size() method after deletion, it indicates that deletion has not been performed
System.out.println("There are no nodes you want to delete");
}
}
🍈 Empty linked list
Violent emptying, directly empty the head node, so that the whole linked list can not be found
//Empty linked list
public void clear(){
this.head = null;
}
The difference and relation between sequential list and linked list
Sequence table
Sequence table: a white cover a hundred ugly
White: continuous space, support random access
Ugly: 1. The insertion and deletion time complexity of the middle or front part is O (n). 2. The cost of capacity expansion is relatively large.
Linked list
Linked list: one (fat black) destroys all
Fat black: it is stored in nodes and does not support random access
All: 1. The time complexity of inserting and deleting at any position is O (1). 2. There is no capacity increase problem. Insert one to open up a space.
🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙
❤ Originality is not easy. If there is any error, please leave a message in the comment area. Thank you very much ❤
❤ If you think the content is good, it's not too much to give a three company~ ❤
❤ I'll pay a return visit when I see it~ ❤
🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙