1. Bracket matching problem

LeetCode link: [20. Valid brackets]

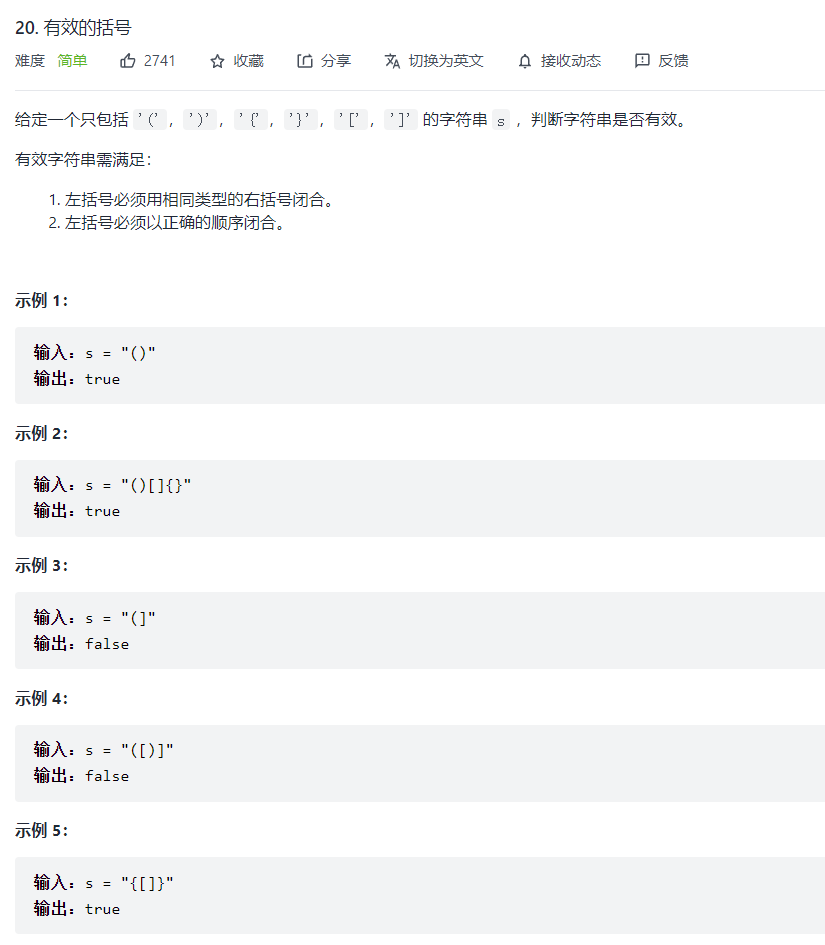
This problem is a classic example of using stack to solve problems; The idea is as follows:
Traverse the string. If it meets the inverted left parenthesis, it will be put on the stack. If it meets the inverted right parenthesis, it will take the element at the top of the stack to match and get the element at the top of the stack. If it matches, it will continue. If it does not match, it will return false.
However, it should be noted that this can only be done when the number of left and right parentheses is equal. What if the number of left and right parentheses is not equal?

• If there are more left parentheses than right parentheses, and they all match after traversal, this situation is not exactly matched, because there are elements left in the stack; Therefore, after traversing the string, add a to judge whether the stack is empty. As long as the stack is empty, all matches are completed and there is no remaining. For example: "[[[[(())"
• If the right parenthesis is more than the left parenthesis, the stack may be empty, and there are no elements in the stack to take, which is also mismatched. Therefore, before taking the top element of the stack, add a to judge whether the stack is empty. If the stack is empty, it means that the right parenthesis is more than the left parenthesis, which is mismatched. For example: "(([[]]]]]]“

The code implementation is as follows:

//There is no stack in C language. Let's implement a stack first
//The build stack is as follows:
typedef char STDataType;
struct Stack
{
	STDataType* a;
	int top;
	int capacity;
};
typedef struct Stack ST;

//Initialization stack
void StackInit(ST* ps);
//Destroy stack
void StackDestory(ST* ps);
//Push 
void StackPush(ST* ps, STDataType x);
//Out of stack
void StackPop(ST* ps);
//Gets the number of elements in the stack
int StackSize(ST* ps);
//Gets the element at the top of the stack
STDataType StackTop(ST* ps);
//Determine whether the stack is empty
bool StackEmpty(ST* ps);

void StackInit(ST* ps)
{
	ps->a = NULL;
	ps->capacity = 0;
	ps->top = 0;
}

void StackDestory(ST* ps)
{
	free(ps->a);
	ps->a = NULL;
	ps->capacity = ps->top = 0;
}

void StackPush(ST* ps,STDataType x)
{
	assert(ps);
	if (ps->capacity == ps->top)
	{
		ps->capacity = ps->capacity > 0 ? ps->capacity * 2 : 2;
		STDataType* tmp = 
		(STDataType*)realloc(ps->a, ps->capacity * sizeof(STDataType));
		if (tmp == NULL)
		{
			return;
		}
		else
		{
			ps->a = tmp;
		}
	}

	ps->a[ps->top] = x;
	ps->top++;
}

void StackPop(ST* ps)
{
	assert(ps);
	assert(ps->top > 0);
	ps->top--;
}

int StackSize(ST* ps)
{
	assert(ps);
	assert(ps->top > 0);
	return ps->top;
}

STDataType StackTop(ST* ps)
{
	assert(ps);
	assert(ps->top > 0);
	return ps->a[ps->top - 1];
}

bool StackEmpty(ST* ps)
{
	assert(ps);
	return ps->top == 0;
}



bool isValid(char * s){
    ST st;
    StackInit(&st);
    while(*s!='\0')
    {
        switch(*s)
        {
            //Stack pressing
            case '(':
            case '[':
            case '{':
            StackPush(&st,*s);
            s++;
            break;
            //Take the data at the top of the stack for matching
            case ')':
            case ']':
            case '}':
            //Out of the stack, take parentheses from the stack. The elements in the stack cannot be empty,
            //Prevent too many right parentheses, resulting in no elements in the stack, which is also a mismatch
            if(StackEmpty(&st))
            {
                return false;
            }
            //Compare the data and characters at the top of the stack
            char top=StackTop(&st);
            StackPop(&st);
            if(top=='(' && *s==')' || 
               top=='[' && *s==']' ||
               top=='{' && *s=='}'
            )
            {
                s++;
            }
            else
            {
                return false;
            }
        }
    }
     
     //Finally, determine whether the stack is empty
     //If the stack is empty, the description will match completely. If there are more left parentheses, it will not match
    if(StackEmpty(&st))
    {
        return true;
    }
    else
    {
        return false;
    }

}

2. Implement stack with queue

LeetCode link: [225. Implement stack with queue]

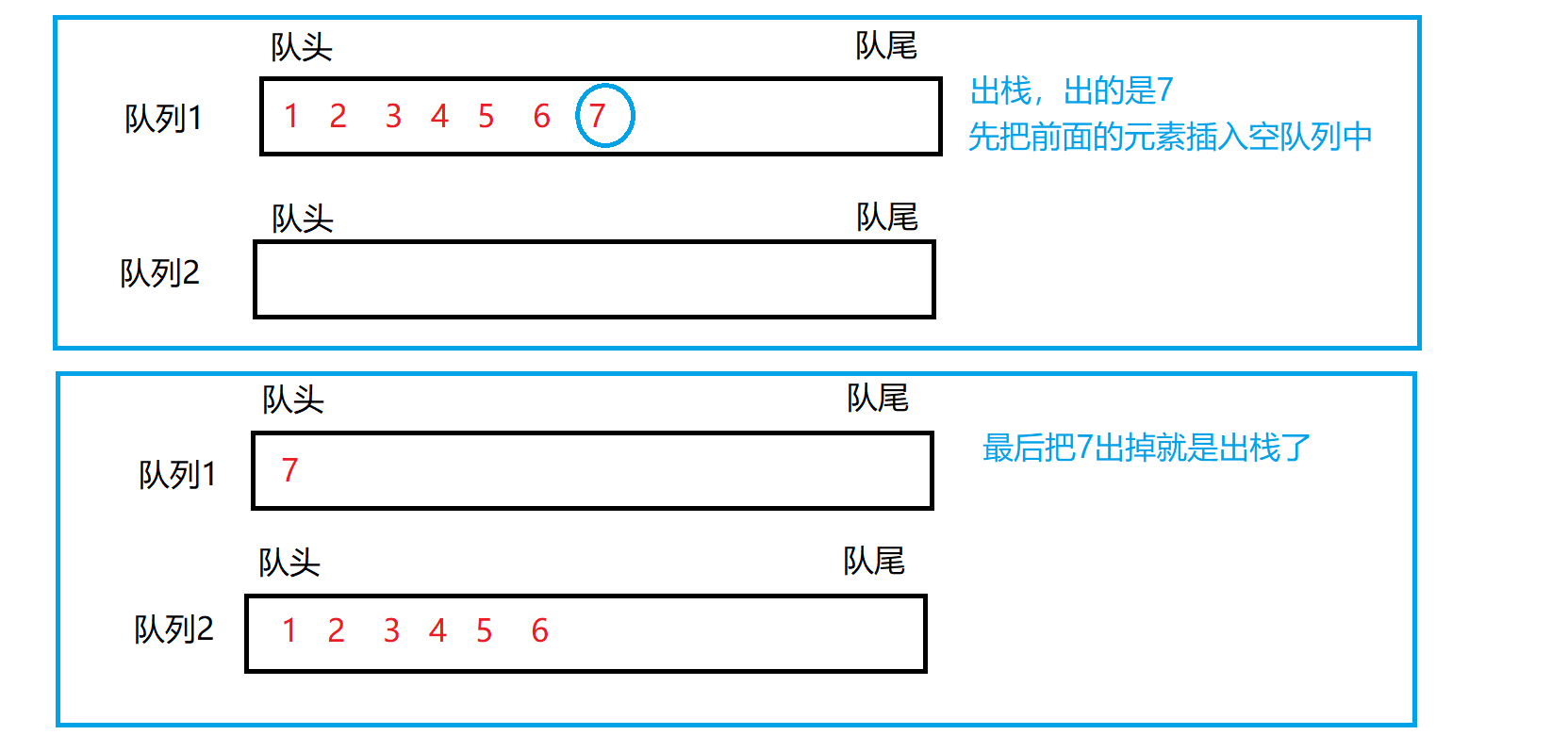
Idea: This requires us to use the nature of queue to realize stack. The nature of queue is first in first out, while the nature of stack is last in first out;
Therefore, we use two queues to realize the stack, one is an empty queue and the other is not an empty queue; entering the stack: entering the non empty queue, and exiting the stack is: only the last element of the non empty queue is retained, and the previous elements are inserted into the empty queue; then exiting the last element is exiting the stack.

The code implementation is as follows:

//There is no queue in C language. Let's build various interfaces of a queue first
//The queue implementation is as follows:
typedef int DataType;
typedef struct Node
{
	struct Node* next;
	DataType data;
}Node;

typedef struct Queue
{
	Node* phead;
	Node* tail;
}Queue;

//Initialize queue
void QueueInit(Queue* pq);  
//Destroy queue
void QueueDestroy(Queue* pq);
//Queue insert data
void QueuePush(Queue* pq,DataType x);
//Queue out data
void QueuePop(Queue* pq);
//Fetch tail data
DataType QueueBack(Queue* pq);
//Fetch header data
DataType QueueFront(Queue* pq);
//Get the number of elements in the queue
int QueueSize(Queue* pq);
//Determine whether the queue is empty
bool QueueEmpty(Queue* pq);

void QueueInit(Queue* pq)
{
	assert(pq);
	pq->phead = NULL;
	pq->tail = NULL;
}

void QueuePush(Queue* pq, DataType x)
{
	Node* tmp = (Node*)malloc(sizeof(Node));
	if (tmp == NULL)
	{
		perror("malloc ");
		exit(-1);
	}
	tmp->data = x;
	tmp->next = NULL;
	if (pq->tail == NULL)
	{
		pq->phead = tmp;
		pq->tail = tmp;
	}
	else
	{
		pq->tail->next = tmp;
		pq->tail = tmp;
	}
}

void QueuePop(Queue* pq)
{
	assert(pq);
	assert(pq->phead);
	// One node
	if (pq->phead->next == NULL)
	{
		free(pq->phead);
		pq->phead = NULL;
		pq->tail = NULL;
	}
	//Multiple nodes
	else
	{
		Node* tmp = pq->phead->next;
		free(pq->phead);
		pq->phead = tmp;
	}
}

int QueueSize(Queue* pq)
{
	assert(pq);
	int count = 0;
	Node* cur = pq->phead;
	while (cur != NULL)
	{
		cur = cur->next;
		count++;
	}
	return count;
}

bool QueueEmpty(Queue* pq)
{
	assert(pq);
	return pq->phead == NULL;
}

DataType QueueFront(Queue* pq)
{
	assert(pq);
	assert(pq->phead);
	return pq->phead->data;
}

DataType QueueBack(Queue* pq)
{
	assert(pq);
	assert(pq->phead);
	return pq->tail->data;
}

void QueueDestroy(Queue* pq)
{
	assert(pq);
	Node* tmp = pq->phead;
	while (tmp != NULL)
	{
		Node* next = tmp->next;
		free(tmp);
		tmp = next;
	}
	pq->phead = pq->tail = NULL;
}
//The above is to implement various interfaces of the queue

//The following is a stack implementation using two queues
//Two queues are used to realize the stack, and the elements of the two queues can be continuously inverted
typedef struct {
    Queue q1;
    Queue q2;
} MyStack;


MyStack* myStackCreate() {
    MyStack* tmp=(MyStack*)malloc(sizeof(MyStack));
    if(tmp==NULL)
    {
        perror("erron ");
        exit(-1);
    }
    QueueInit(&tmp->q1);
    QueueInit(&tmp->q2);
    return tmp;
}

//Insert data into a queue that is not empty. If both queues are empty, either one will do
void myStackPush(MyStack* obj, int x) {
    Queue* empty=&obj->q1;
    Queue* nonempty=&obj->q2;
    if(QueueEmpty(&obj->q2))
    {
        Queue* empty=&obj->q2;
        Queue* nonempty=&obj->q1;
    }
    QueuePush(nonempty,x);
  

}

//First, pour the data from the non empty queue into the empty queue until there is only one element left
//The last element of the queue that is not empty is the element at the top of the stack. Just drop it
int myStackPop(MyStack* obj) {
    Queue* empty=&obj->q1;
    Queue* nonempty=&obj->q2;
    if(QueueEmpty(&obj->q2))
    {
         empty=&obj->q2;
         nonempty=&obj->q1;
    }
    while(QueueSize(nonempty)>1)
    {
        QueuePush(empty,QueueFront(nonempty));
        QueuePop(nonempty);
    }
    //The last element is the element at the top of the stack
    //Just exit to ensure that there is an empty queue in the queue
    int tmp=QueueBack(nonempty);
    QueuePop(nonempty);
    return tmp;

}

//Just take the tail element of the queue that is not empty
int myStackTop(MyStack* obj) {
   Queue* empty=&obj->q1;
   Queue* nonempty=&obj->q2;
   if(QueueEmpty(&obj->q2))
    {
        empty=&obj->q2;
        nonempty=&obj->q1;
    }
    return QueueBack(nonempty);
}

bool myStackEmpty(MyStack* obj) {
    //If both queues are empty, the stack is empty
    return QueueEmpty(&obj->q1)  && QueueEmpty(&obj->q2);
}

void myStackFree(MyStack* obj) {
    QueueDestroy(&obj->q1);
    QueueDestroy(&obj->q2);
    free(obj);
}

3. Implement queue with stack

LeetCode link: [232. Implement queue with stack]

The train of thought is analyzed as follows:

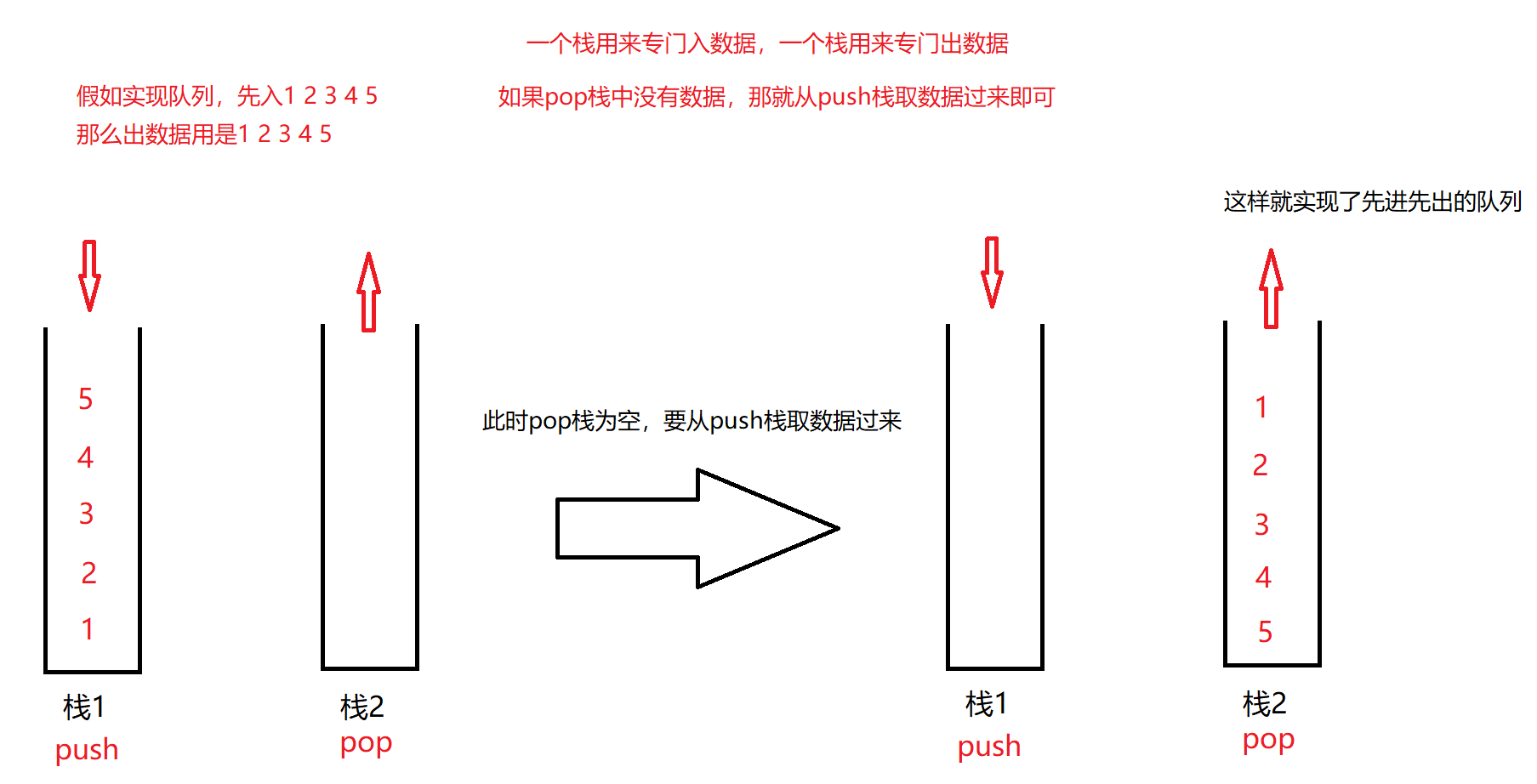
The code implementation is as follows:

//There is no stack in C language. Let's implement a stack first
//The build stack is as follows:
typedef int STDataType;
struct Stack
{
	STDataType* a;
	int top;
	int capacity;
};
typedef struct Stack ST;

//Initialization stack
void StackInit(ST* ps);
//Destroy stack
void StackDestory(ST* ps);
//Push 
void StackPush(ST* ps, STDataType x);
//Out of stack
void StackPop(ST* ps);
//Gets the number of elements in the stack
int StackSize(ST* ps);
//Gets the element at the top of the stack
STDataType StackTop(ST* ps);
//Determine whether the stack is empty
bool StackEmpty(ST* ps);

void StackInit(ST* ps)
{
	ps->a = NULL;
	ps->capacity = 0;
	ps->top = 0;
}

void StackDestory(ST* ps)
{
	free(ps->a);
	ps->a = NULL;
	ps->capacity = ps->top = 0;
}

void StackPush(ST* ps,STDataType x)
{
	assert(ps);
	if (ps->capacity == ps->top)
	{
		ps->capacity = ps->capacity > 0 ? ps->capacity * 2 : 2;
		STDataType* tmp = 
		(STDataType*)realloc(ps->a, ps->capacity * sizeof(STDataType));
		if (tmp == NULL)
		{
			return;
		}
		else
		{
			ps->a = tmp;
		}
	}

	ps->a[ps->top] = x;
	ps->top++;
}

void StackPop(ST* ps)
{
	assert(ps);
	assert(ps->top > 0);
	ps->top--;
}

int StackSize(ST* ps)
{
	assert(ps);
	assert(ps->top > 0);
	return ps->top;
}

STDataType StackTop(ST* ps)
{
	assert(ps);
	assert(ps->top > 0);
	return ps->a[ps->top - 1];
}

bool StackEmpty(ST* ps)
{
	assert(ps);
	return ps->top == 0;
}



//Two stacks. Reverse the non empty stack to the empty stack, which is the queue
//Design two stacks, one for incoming data and one for outgoing data
//Input data into pushst stack and output data out of popst stack
typedef struct {
    ST Pushst; //Input data stack
    ST Popst;  //Out of data stack
} MyQueue;

MyQueue* myQueueCreate() {
    MyQueue* tmp=(MyQueue*)malloc(sizeof(MyQueue));
    if(tmp==NULL)
    {
        perror("erron ");
        exit(-1);
    }
    StackInit(&tmp->Pushst);
    StackInit(&tmp->Popst);
    return tmp;
}

void myQueuePush(MyQueue* obj, int x) {
    StackPush(&obj->Pushst,x);
}

//To check whether the stack of data is empty, if there is no data, take it from the stack of data
int myQueuePop(MyQueue* obj) {
    if(StackEmpty(&obj->Popst))
    {
        while(!StackEmpty(&obj->Pushst))
        {
            StackPush(&obj->Popst,StackTop(&obj->Pushst));
            StackPop(&obj->Pushst);
        }
    }
    int tmp=StackTop(&obj->Popst);
    StackPop(&obj->Popst);
    return tmp;
}

//Take the header element of the queue and check whether the stack of data is empty. If there is no data, take it from the stack of data
int myQueuePeek(MyQueue* obj) {
    if(StackEmpty(&obj->Popst))
    {
        while(!StackEmpty(&obj->Pushst))
        {
            StackPush(&obj->Popst,StackTop(&obj->Pushst));
            StackPop(&obj->Pushst);
        }
    }
    return StackTop(&obj->Popst);
}

bool myQueueEmpty(MyQueue* obj) {
    return StackEmpty(&obj->Pushst) && StackEmpty(&obj->Popst);
}

void myQueueFree(MyQueue* obj) {
    StackDestroy(&obj->Pushst);
    StackDestroy(&obj->Pushst);
    free(obj);
}

4. Design cyclic queue

LeetCode link: [622. Design cycle queue]

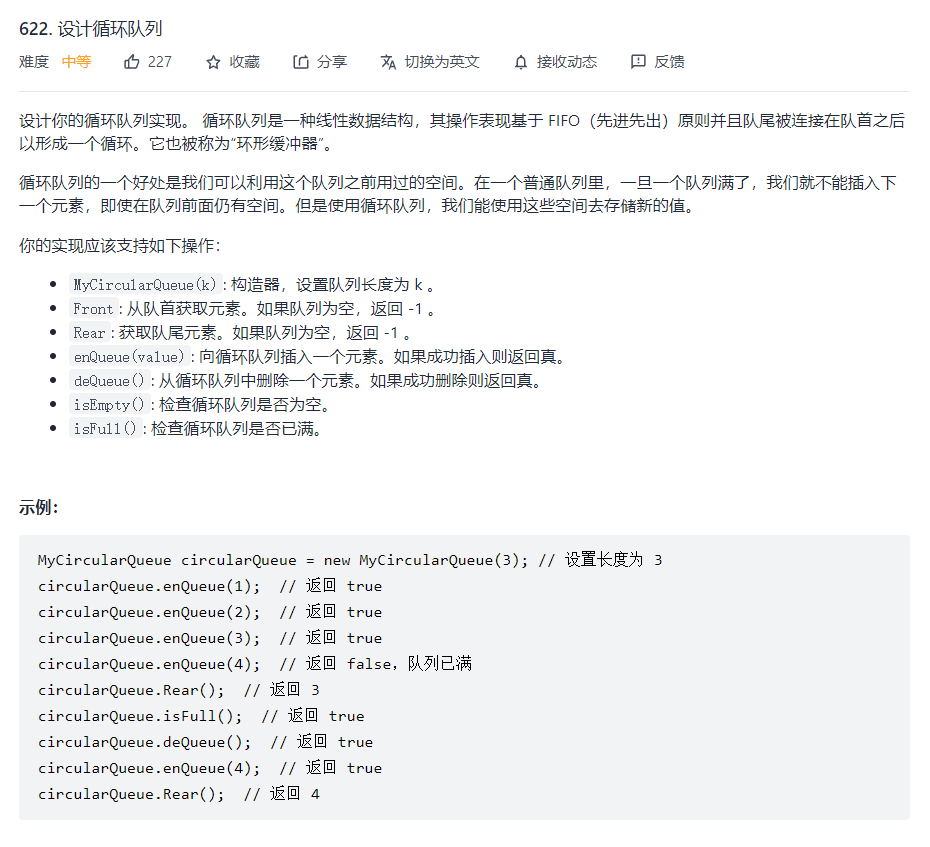
Before doing this problem, let's first understand what is a circular queue. Its explanation is as follows:
Circular queue is to connect the sequential queue end to end, and logically regard the table storing queue elements as a ring to become a circular queue.
Circular queue is to round the last position of the queue storage space to the first position to form a logical ring space for the cyclic use of the queue. In the circular queue structure, when the last position of the storage space has been used and wants to enter the queue operation, only the first position of the storage space is idle, you can add elements to the first position, that is, storage The first position in space is the tail of the team.
Circular queue can prevent pseudo overflow more simply, but the queue size is fixed.

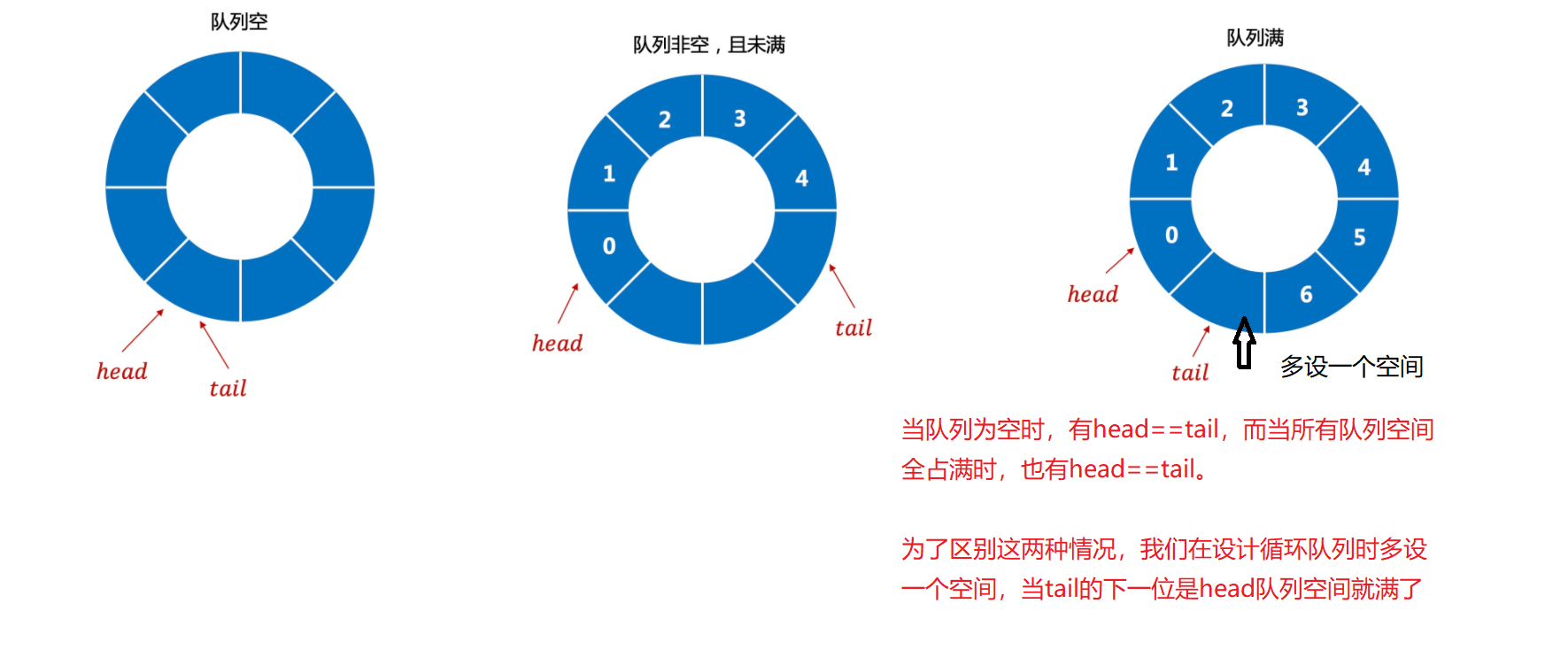
Therefore, the structure of circular queue is clear and easy to write. There are two implementation methods of circular queue, which can be implemented by array or circular linked list. They are introduced below.
The linked list is implemented as follows:

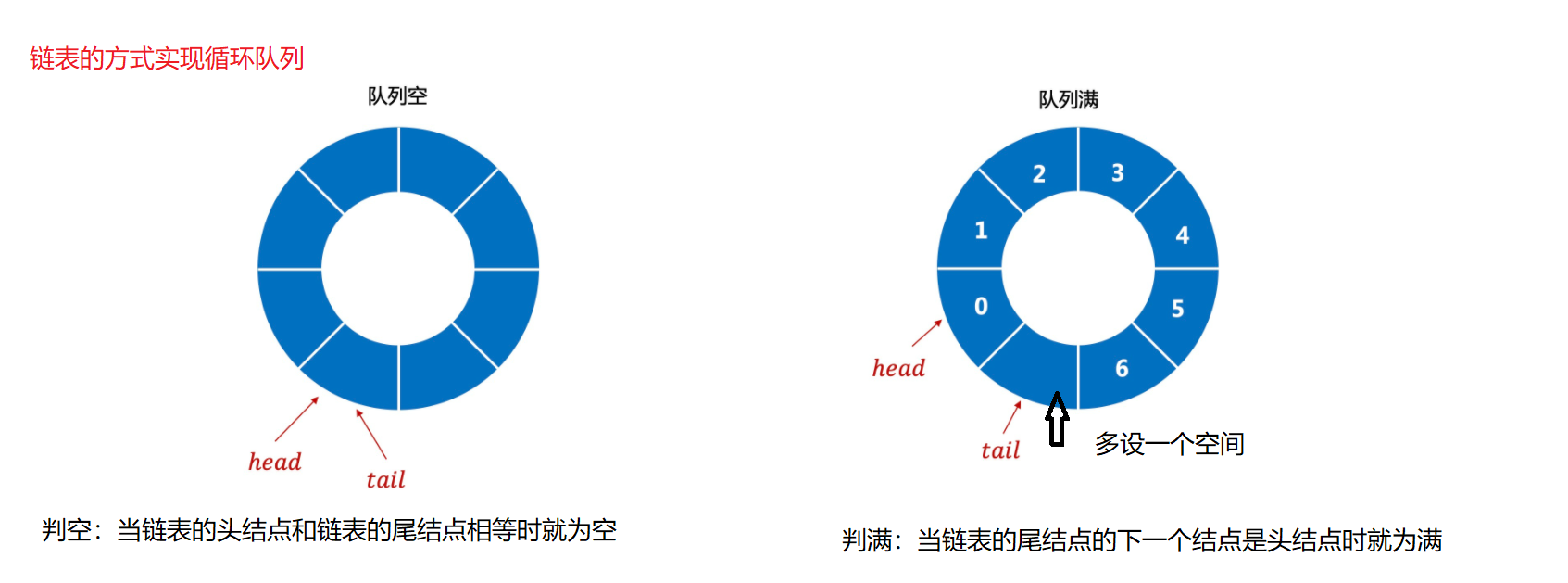
//Create a node type first
typedef struct Node
{
    struct Node* next;
    int data;
}Node;


//Create a circular queue type structure
//The head pointer points to the head of the linked list and the tail pointer points to the tail of the linked list
typedef struct {
    Node* front;
    Node* tail;
} MyCircularQueue;


//Create circular queue
MyCircularQueue* myCircularQueueCreate(int k) {
    MyCircularQueue* tmp=(MyCircularQueue*)malloc(sizeof(MyCircularQueue));

    //Construct a linked list
    //One more node should be constructed, or you can't judge whether it is full
    Node* head=(Node*)malloc(sizeof(Node));
    Node* a=head;
    Node* tail=head;
    while(k--)
    {
        a=tail;
        tail=(Node*)malloc(sizeof(Node));
        a->next=tail;
    }
    tail->next=head;

    tmp->front=head;
    tmp->tail=head;
    return tmp;

}

//Inserts an element into the circular queue
bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {
    if(obj->tail->next==obj->front)
    {
        return false;
    }
    obj->tail->data=value;
    obj->tail=obj->tail->next;
    return true;

}

//Deletes an element from the loop queue
bool myCircularQueueDeQueue(MyCircularQueue* obj) {
    if(obj->front==obj->tail)
    {
        return false;
    }
    obj->front=obj->front->next;
    return true;

}

//Get element from team leader
int myCircularQueueFront(MyCircularQueue* obj) {
   if(obj->front==obj->tail)
    {
        return -1;
    }
    return obj->front->data;

}

//Get tail element
int myCircularQueueRear(MyCircularQueue* obj) {
    if(obj->front==obj->tail)
    {
        return -1;
    }
    //The first node to find the end of the queue is the end of the queue data
    Node* cur=obj->front;
    while(cur->next!=obj->tail)
    {
        cur=cur->next;
    }
    return cur->data;

}

//Check whether the circular queue is empty
bool myCircularQueueIsEmpty(MyCircularQueue* obj) {
    return obj->front==obj->tail;

}

//Check if the circular queue is full.
bool myCircularQueueIsFull(MyCircularQueue* obj) {
    return obj->tail->next==obj->front;

}

//Free memory
void myCircularQueueFree(MyCircularQueue* obj) {
    Node* cur=obj->front;
    while(cur!=obj->tail)
    {
        Node* next=cur->next;
        free(cur);
        cur=next;
    }
    free(cur);
    free(obj);
}

The array method is implemented as follows:

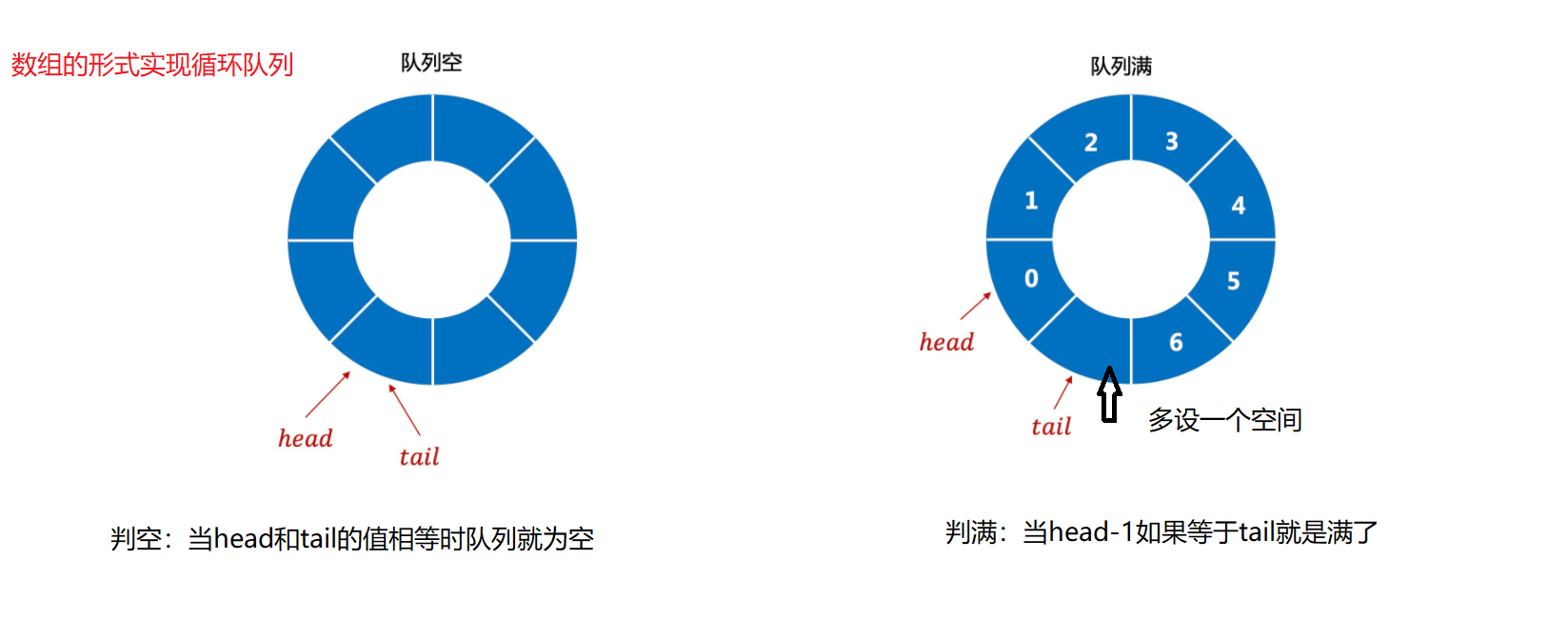
The code implementation is as follows:

//In the circular queue structure, a pointer is designed to point to a continuous space
typedef struct {
    int* a;
    int maxSize;
    int head;
    int tail;
} MyCircularQueue;

bool myCircularQueueIsFull(MyCircularQueue* obj);

//Create circular queue
MyCircularQueue* myCircularQueueCreate(int k) {
    MyCircularQueue* tmp=
    (MyCircularQueue*)malloc(sizeof(MyCircularQueue)); 
    //We should open up one more space
    int* arr=(int*)malloc(sizeof(int)*(k+1));
    tmp->a=arr;
    tmp->maxSize=k+1;
    tmp->head=0;
    tmp->tail=0;
    return tmp;
}

//Inserts an element into the circular queue
bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {
    if(myCircularQueueIsFull(obj))
    {
        return false;
    }
    obj->a[obj->tail]=value;
    obj->tail++;
    //The subscript tail is controlled in the array and cannot exceed the bounds
    if(obj->tail==obj->maxSize)
    {
        obj->tail=0;
    }
    return true;
}

//Deletes an element from the loop queue
bool myCircularQueueDeQueue(MyCircularQueue* obj) {
    if(obj->head==obj->tail)
    {
        return false;
    }
    obj->head++;
    if(obj->head==obj->maxSize)
    {
        obj->head=0;
    }
    return true; 
}

//Get element from team leader
int myCircularQueueFront(MyCircularQueue* obj) {
    if(obj->head==obj->tail)
    {
        return -1;
    }
    return obj->a[obj->head];

}

//Get tail element
int myCircularQueueRear(MyCircularQueue* obj) {
    if(obj->head==obj->tail)
    {
        return -1;
    }
    int i=0;
    if(obj->tail==0)
    {
        i=obj->maxSize-1;
    }
    else
    {
        i=obj->tail-1;
    }
    return obj->a[i];
}

//Check whether the circular queue is empty
bool myCircularQueueIsEmpty(MyCircularQueue* obj) {
    return obj->head==obj->tail;
}

//Check if the circular queue is full
bool myCircularQueueIsFull(MyCircularQueue* obj) {
   //Method 1: judge whether it is full
   // return obj->head==(obj->tail+1)%obj->maxSize;

    
    //Method 2: judge whether it is full
    int head=0;
    if(obj->head==0)
    {
        head=obj->maxSize-1;
    }
    else
    {
        head=obj->head-1;
    }
    return head==obj->tail;

}

void myCircularQueueFree(MyCircularQueue* obj) {
    free(obj->a);
    free(obj);
}