subject

Problem solving

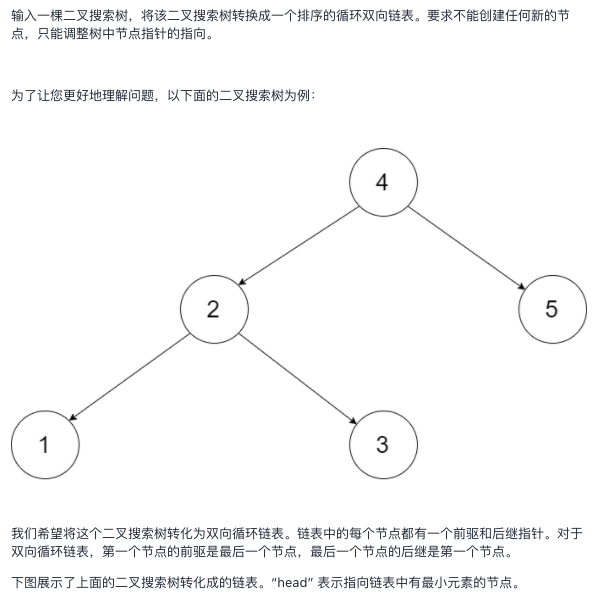
A "binary tree middle order traversal problem", which is unfamiliar to binary tree middle order traversal, I suggest moving first Middle order traversal of LeetCode94 binary tree.

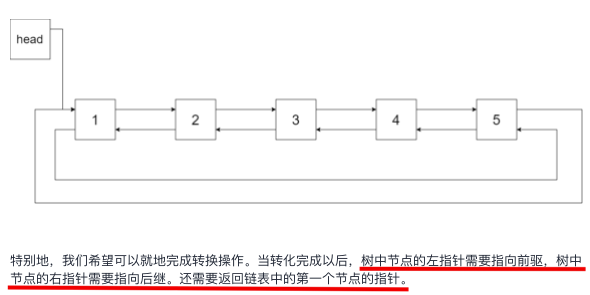
Question 94 is to output node values in the form of an array in the order of traversal in the middle order. The difference in this problem is that it is necessary to build a circular two-way linked list structure. The left pointer is equivalent to the prev pointer, and the right pointer is equivalent to the next pointer. In addition, the head and tail should be connected (record the head and tail, and finally connect them).

Therefore, the task to be completed in the step of adding the node val value to the array becomes: the current node is marked as a, A.left = the last added node B (if not null), B.right = a; = > Thus, it is analyzed that the previous node needs to be recorded (just in line with the meaning of the node recorded by the tail pointer). When processing a, A.left, that is, its left subtree has been processed, so the left pointer can be changed, but the right subtree will be traversed after a (the nature of binary search tree), so the right pointer can only be changed when processing the next node.

In addition, pay special attention to the empty tree when connecting end to end.

Solution 1: recursion

// javascript
var treeToDoublyList = function(root) {
    if (root === null) return null;    // Binary search tree is empty
    let head = null, tail = null;      // Record the head and tail of the two-way linked list
    const dfs = (root) => {
    	if (root === null) return;
    	// First traverse the left subtree
        dfs(root.left);
        // After traversing the left subtree, the next one to be processed is root
        if (head === null) {           // If the header pointer is null, it indicates that root is the header node (the first node to be processed)
            head = root;
        }
        if (tail !== null) {           // Only when the tail pointer is not null: the right of the precursor node can be pointed to the current node when there is a precursor node (null has no right pointer)
            root.left = tail;
            tail.right = root;
        }
        tail = root;                   // Update tail pointer (to the last processed node)
        // Then traverse the right subtree
        dfs(root.right);   
    };
    dfs(root);
    // End to end. Since the tree is empty, it has been handled at the beginning, so neither head nor tail is null
    head.left = tail;
    tail.right = head;
    return head;
};

Solution 2: stack

Recursion implicitly calls the stack. Similarly, we can imitate the recursion order and explicitly present the stack: the recursion order is to find the left subtree first. If the left subtree is empty, return to the root node. After the root node is processed, process the right subtree of the root node, and return to the root node of a higher level after the right subtree is processed.

So the problem is that we need to record the parent node: otherwise we can't return! This is what the recursive stack does. Next, we directly use stack to complete this function, and the processing order is to first process the low-level root node and then the high-level root node, which is just in line with the characteristics of stack first in and then out.

// javascript
var treeToDoublyList = function(root) {
    const visit = (cur) => {
        if (head === null) {
            head = cur;
        }
        if (tail !== null) {
            cur.left = tail;
            tail.right = cur;
        }
        tail = cur;
    };
    if (root === null) return null;
    const stk = new Array();
    let head = null, tail = null;
    while (root !== null || stk.length > 0) {
    	// Depth first to find the left subtree, and record the root nodes in the stack in turn
        while (root !== null) {
            stk.push(root);
            root = root.left;
        }
        // The root passed in at the beginning = null
        // Or in the process of finding the left subtree, after processing the left subtree of the lowest layer, the root is updated to null
        root = stk.pop();
        visit(root);
        root = root.right;
    }
    head.left = tail;
    tail.right = head;
    return head;
};

Solution 3: order traversal in Morris

Note that the order of operations 1 and 2 in the code comments cannot be exchanged: at this time, the predecessor is the precursor node of root (tail points to the predecessor). When calling visit, the right pointer of the precursor node will point to root. If you change the predecessor.right to null after visit, it is equivalent to disconnecting the connection again.

// javascript
var treeToDoublyList = function(root) {
	// Encapsulate a visit function
    const visit = (cur) => {
        if (head === null) {
            head = cur;
        }
        if (tail !== null) {
            tail.right = cur;
            cur.left = tail;
        }
        tail = cur;
    };

    let head = null, tail = null;
    while (root !== null) {
        if (root.left !== null) {
            let predecessor = root.left;
            while (predecessor.right !== null && predecessor.right !== root) {
                predecessor = predecessor.right;
            }
            if (predecessor.right === null) {
                predecessor.right = root;
                root = root.left;
            } else {
            	// Because while has two exit conditions
            	// Else is also equivalent to else if (predecessor.right === root)
            	// The order of operations 1 and 2 cannot be exchanged
                predecessor.right = null;  // Operation 1
                visit(root);               // Operation 2
                root = root.right;
            }
        } else {
            visit(root);
            root = root.right;
        }
    }
    // End to end connection is equivalent to taking the head as the last node of the tail, and you can call visit again
    // And visit can handle empty trees
    // If you want to write head.left = tail as before; tail.right = head;
    // Be sure to deal with the special case of empty trees first
    visit(head);
    return head;
};