Operating environment

Pycharm + Anaconda3

A set of fuzzy sets of sludge and oil parameters and the corresponding washing time reasoning results are known.

Now a group of fuzzy sets of sludge and grease are given, fuzzy reasoning is carried out, and the fuzzy set of washing time is deduced.

Finally, the fuzzy decision is made to select the grade of washing time, and the maximum membership degree and weighted average method are used

1. Fuzzy control rules

"The more sludge / grease, the longer the washing time";
"Moderate sludge / grease, moderate washing time";
"The less sludge / grease, the shorter the washing time".

Test example:
Sludge = [0,0.83,0.6]
Grease = [0, 0.71, 0.7]

Sludge and grease are divided into three grades: 1, 2 and 3, respectively indicating low, medium and high degree
The washing time is divided into five grades. 1, 2, 3, 4 and 5 respectively mean that the time is very short, short, medium, high and high

The fuzzy set sludge [0, 0.5, 1], grease [0, 0.5, 1], washing time [0, 0.25, 0.5, 0.75, 1] are given

The value represents the membership degree, and the corresponding element is omitted.

Program running logic diagram

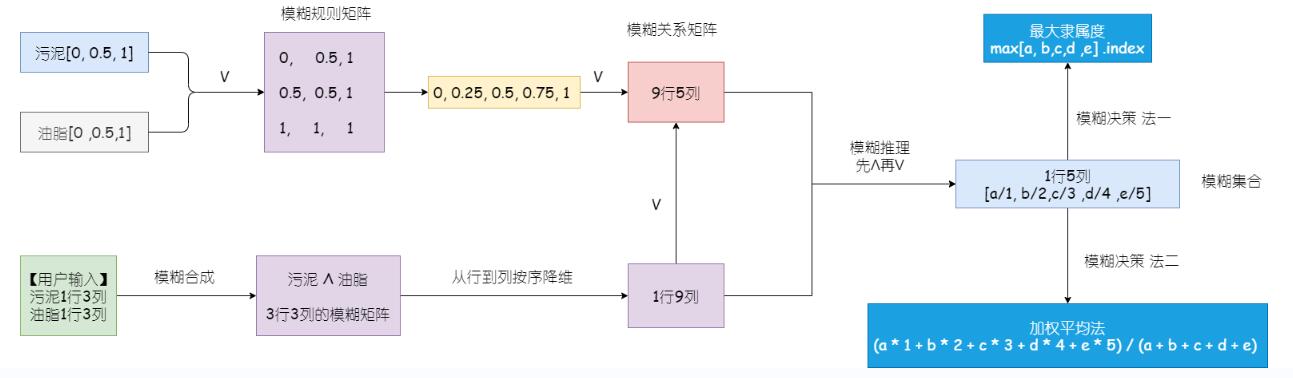
2. Fuzzy rule control matrix

The matrix is the result of fuzzy synthesis of two fuzzy sets of sludge and oil, which adopts the large operation (V).
Implementation code

def getRuleMatrix(a, b, r, c):
    data = np.zeros(shape=(r, c), dtype=float)
    for i in range(len(a)):
        for j in range(len(b)):
                data[i][j] = max(a[i], b[j])
    return data
A = getRuleMatrix([0, 0.5, 1], [0, 0.5, 1], 3, 3)

result
[[0. 0.5 1. ]
[0.5 0.5 1. ]
[1. 1. 1. ]]

3. Fuzzy relation

The fuzzy relationship between the rule control matrix and the washing time represents the result of fuzzy synthesis between the fuzzy set after fuzzy synthesis of sludge and oil and the washing time

It should be noted that the second operation is the calculation of [3 x 3] matrix and [1 x 5] matrix. Here, dimension reduction is used to convert [3 x 3] into [9 x 1], so that fuzzy synthesis can be carried out with [1 x 5] matrix, and finally a [9 x 5] fuzzy relationship matrix is generated. And this time, λ is smaller.
Implementation code

def getRelation(A, B):
    A = [y for x in A for y in x]
    data = np.zeros(shape=(len(A), len(B)), dtype=float)
    for i in range(len(A)):
        for j in range(len(B)):
                data[i][j] = min(A[i], B[j])
    return data
B = getRelation(A, [0, 0.25, 0.5, 0.75, 1])

result
[[0. 0. 0. 0. 0. ]
[0. 0.25 0.5 0.5 0.5 ]
[0. 0.25 0.5 0.75 1. ]
[0. 0.25 0.5 0.5 0.5 ]
[0. 0.25 0.5 0.5 0.5 ]
[0. 0.25 0.5 0.75 1. ]
[0. 0.25 0.5 0.75 1. ]
[0. 0.25 0.5 0.75 1. ]
[0. 0.25 0.5 0.75 1. ]]

4. Fuzzy reasoning

The so-called fuzzy reasoning is two fuzzy synthesis according to the fuzzy set of sludge and oil in the second group.

For the first time, fuzzy synthesis is carried out between sludge and grease to generate a [3 x 3] matrix, where the dimension is reduced to [1 x 9].

The second time, the fuzzy relation matrix of the first time and the previous [9 x 5] fuzzy relation matrix are used for fuzzy reasoning (Λ before V)

Finally, a [1 x 5] matrix is obtained, such as [a, b, c, d, e], where the value represents the membership degree for each washing time

For example, if e = 0.8, it means that the washing time is likely to be fast.

Fuzzy reasoning implementation code

def getResult(A, B):
    A = [y for x in A for y in x]
    data = [-1 for _ in range(len(B[0]))]
    for j in range(len(B[0])):
        for i in range(len(A)):
            data[j] = max(data[j], min (A[i], B[i][j]))
    return data

sludge = [float(x) for x in input('Input sludge index:').split(" ")]
grease = [float(x) for x in input('Input grease index: ').split(" ")]

AA = getRuleMatrix(sludge, grease, 3, 3)
BB = getResult(AA, B)

result
AA
[[0. 0.71 0.7 ]
[0.83 0.83 0.83]
[0.6 0.71 0.7 ]]
BB
[0.0, 0.25, 0.5, 0.75, 0.83]

5. Fuzzy decision

The fuzzy decision is made according to the fuzzy set of the last washing time.

5.1 maximum membership method

Select the element with the largest membership. Based on the previous code and BB list, it represents the final washing time fuzzy set, in which the value represents the membership
[0, 0.25, 0.5, 0.75, 0.83] respectively correspond to the degree of five washing times, very short 1, short 2, medium 3, fast 4 and fast 5.
Obviously, 0.83 is the largest degree of membership, so the result is 5.
Implementation code

[i+1 for i in range(len(BB)) if BB[i] == max(BB)][0]

5.2 weighted average method

Taking [0, 0.25, 0.5, 0.75, 0.83] as an example, the calculation process is (0 * 1 + 0.25 * 2 + 0.5 * 3 + 0.75 * 4 + 0.83 * 5) / (0 + 0.25 + 0.5 + 0.75 + 0.83)

If the final result may contain decimals, it shall be rounded.
Implementation code

int(sum([i * BB[i] for i in range(len(BB))]) / sum(BB) + 0.5)

6. Final code

import numpy as np
def getRuleMatrix(a, b, r, c):
    data = np.zeros(shape=(r, c), dtype=float)
    for i in range(len(a)):
        for j in range(len(b)):
                data[i][j] = max(a[i], b[j])
    return data
def getRelation(A, B):
    A = [y for x in A for y in x]
    data = np.zeros(shape=(len(A), len(B)), dtype=float)
    for i in range(len(A)):
        for j in range(len(B)):
                data[i][j] = min(A[i], B[j])
    return data
A = getRuleMatrix([0, 0.5, 1], [0, 0.5, 1], 3, 3)
B = getRelation(A, [0, 0.25, 0.5, 0.75, 1])

def getResult(A, B):
    A = [y for x in A for y in x]
    data = [-1 for _ in range(len(B[0]))]
    for j in range(len(B[0])):
        for i in range(len(A)):
            data[j] = max(data[j], min (A[i], B[i][j]))
    return data

sludge = [float(x) for x in input('Input sludge index:').split(" ")]
grease = [float(x) for x in input('Input grease index: ').split(" ")]

AA = getRuleMatrix(sludge, grease, 3, 3)
BB = getResult(AA, B)

print('Maximum membership method:' , [i+1 for i in range(len(BB)) if BB[i] == max(BB)][0])
print('Weighted average method:', int(sum([i * BB[i] for i in range(len(BB))]) / sum(BB) + 0.5))