subject

Give you a matrix board of m x n, which consists of several characters' X 'and' O ', find all areas surrounded by' X ', and fill all' O 'in these areas with' X '.

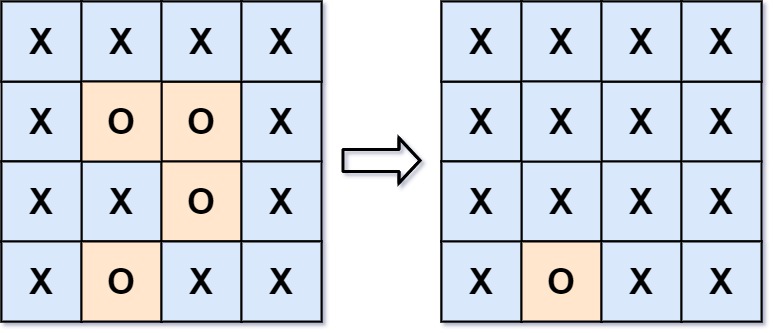
Example 1

Input: board = [["X","X","X","X"],["X","O","O","X"],["X","X","O","X"],["X","O","X","X"]]
Output:[["X","X","X","X"],["X","X","X","X"],["X","X","X","X"],["X","O","X","X"]]
Explanation: the enclosed interval does not exist on the boundary, in other words, on any boundary 'O' Will not be filled with 'X'.  
Anything that is not on the boundary or is not related to the boundary 'O' Connected 'O' Will eventually be filled with 'X'. 
If two elements are adjacent horizontally or vertically, they are said to be "connected"

Example 2

Input: board = [["X"]]
Output:[["X"]]

thinking

First, grasp the important information in the title stem, "the 'O' on any boundary will not be filled as' X ', which means that any' O 'connected to the boundary will not be filled, and here we should also note that the title says" if two elements are adjacent in the horizontal or vertical direction, they are called "connected" ", which means that we don't need to control the elements on the diagonal of the elements. Even if they are connected, they can't be regarded as connected.
Then let's take a look at the practice of this problem. There are two types of 'O' area, one is connected to the boundary and does not change, and the other is not connected to the boundary and needs to be filled with 'X'.
1. For the 'O' connected to the boundary, we need to mark it when searching, or fill it with another letter as a mark, and then restore it when we traverse it at the last time.
2. For 'O' not connected to the boundary, we can directly ignore it when searching, because our search target is actually only 'O' connected to the boundary, and other 'O' will be directly filled with 'X' when traversing the last time.

We have a general idea of how to write dfs. First of all, we need to know our search starting point. The search starting point is all the elements in the outermost circle of this mxn matrix, because we need to search the 'O' connected with the 'O' of the boundary. If the boundary is not 'O', we can directly skip the current boundary without searching, and then after entering dfs, we will search for the current search results Search the points in the up, down, left and right directions until the searched point is' X '. Here is recursive search.
How to write dfs:
First write the exit of dfs. When will we stop dfs
1. When the point searched by dfs does not exist, we search in a matrix such as m x n, so when x or y is less than 0 or exceeds the size of the matrix, the dfs is terminated
2. Because we want to search 'O' connected to the boundary, we can directly end dfs when the current point of dfs search is not 'O'

void dfs(vector<vector<char>>& board, int x,int y) {
	if(x < 0 || x >= m || y < 0 || y >= n || board[x][y] != 'O') {
		return;
	}
}

After the exit is written, we need to write the "action" for the point searched by the current dfs. This "action" means that we search for the point connected to the boundary with the value of 'O', and then we need to change this point

void dfs(vector<vector<char>>& board, int x,int y) {
	if(x < 0 || x >= m || y < 0 || y >= n || board[x][y] != 'O') {
		return;
	}
	board[x][y] = 'A';
}

Based on the above discussion, we want to fill the points connected with the point with the boundary value of 'O' and the point with the value of 'O' with another letter. Here I choose 'A'
After the point is changed, we need to perform a deep recursive search on the top, bottom, left and right of the point

void dfs(vector<vector<char>>& board, int x,int y) {
	if(x < 0 || x >= m || y < 0 || y >= n || board[x][y] != 'O') {
		return;
	}
	board[x][y] = 'A';
	dfs(board, x + 1, y);//lower
	dfs(board, x - 1, y);//upper
	dfs(board, x, y + 1);//right
	dfs(board, x, y - 1);//Left
}

After writing recursion, we will write the main function, that is, what we need to do at the entrance of dfs. As discussed above, we need to start the dfs search from the boundary of the matrix, that is, the four edges of the matrix. The code is as follows

class Solution{
	int m, n;
	void solve(vector<vector<char>>& board) {
		int m = int(board.size());
        int n = int(board[0].size());
        for(int i = 0; i < m; i++) {
            if(board[i][0] == 'O') {
                dfs(board, i, 0);//left
            }
            if(board[i][n - 1] == 'O') {
                dfs(board, i, n - 1);//right
            }
        }
        for(int j = 1; j < n - 1; j++) {
            if(board[0][j] == 'O') {
                dfs(board, 0, j);//Above
            }
            if(board[m - 1][j] == 'O') {
                dfs(board, m - 1, j);//Below
            }
        }
	}
}

An if is added because you can directly judge whether the boundary is' O '. If not, you can directly skip the current boundary point
After completing the above, we need A final traversal to restore the points with the value of 'A' or fill the points with the value of 'O' with 'X'. The total code is as follows:
Full code:

class Solution{
	int m, n;
	void dfs(vector<vector<char>>& board, int x,int y) {
		if(x < 0 || x >= m || y < 0 || y >= n || board[x][y] != 'O') {
			return;
		}
		board[x][y] = 'A';
		dfs(board, x + 1, y);//lower
		dfs(board, x - 1, y);//upper
		dfs(board, x, y + 1);//right
		dfs(board, x, y - 1);//Left
	}
	void solve(vector<vector<char>>& board) {
		int m = int(board.size());
        int n = int(board[0].size());
        for(int i = 0; i < m; i++) {
            if(board[i][0] == 'O') {
                dfs(board, i, 0);//left
            }
            if(board[i][n - 1] == 'O') {
                dfs(board, i, n - 1);//right
            }
        }
        for(int j = 1; j < n - 1; j++) {
            if(board[0][j] == 'O') {
                dfs(board, 0, j);//Above
            }
            if(board[m - 1][j] == 'O') {
                dfs(board, m - 1, j);//Below
            }
        }
        for(int i = 0; i < m; i++) {
            for(int j = 0; j < n; j++) {
                if(board[i][j] == 'A') {
                    board[i][j] = 'O';
                } else {
                    board[i][j] = 'X';
                }
            }
        }
	}
}

Hello, everyone. I'm a programmer Yunjin. I'm a junior majoring in computer science. My direction is the front end and algorithm. In the future, I will update the relevant contents of the front end and algorithm on csdn. I hope you can join me! I'll pay a return visit one by one after the third review! Thank you!!!