catalogue

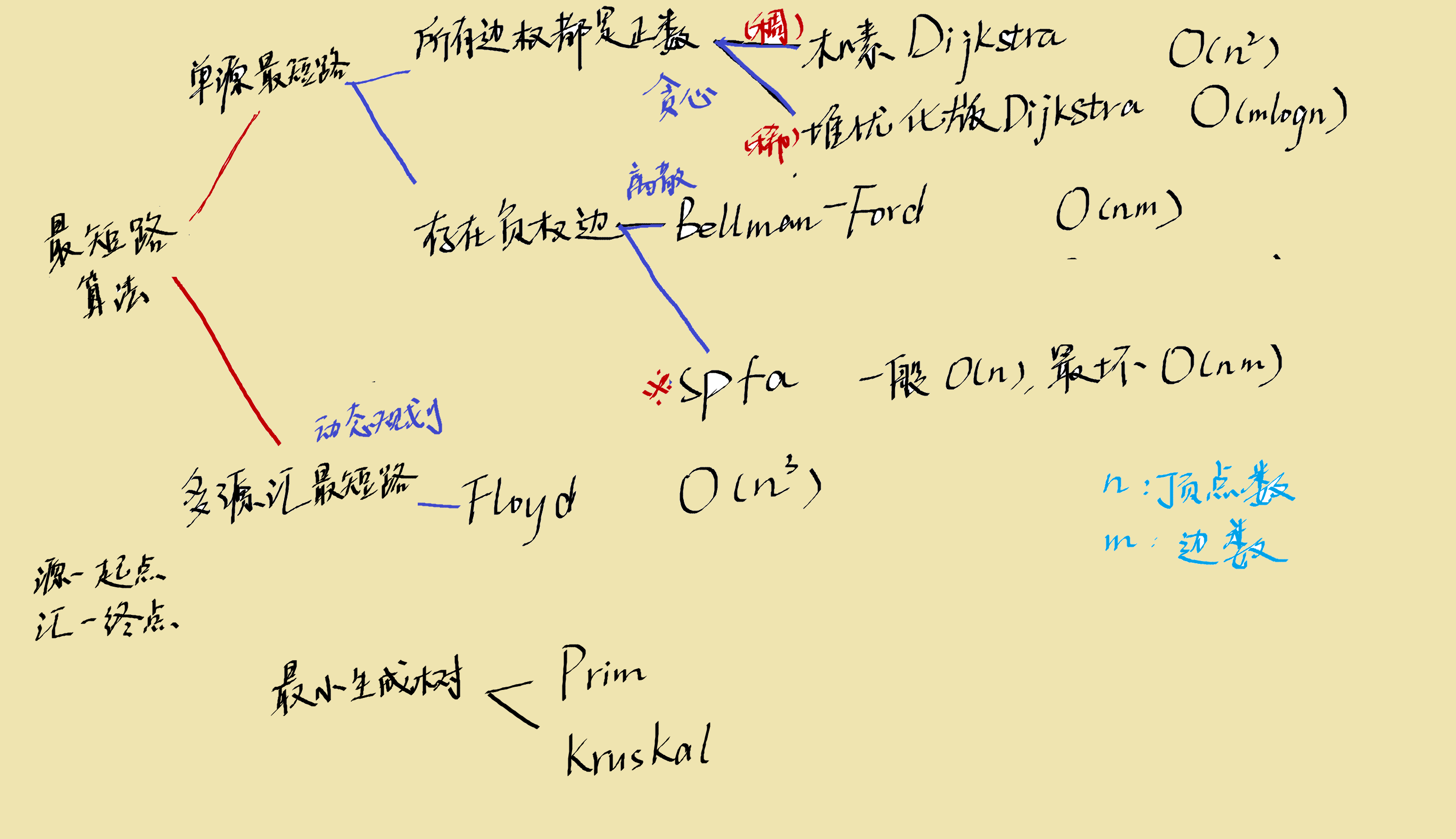
shortest path

Plain Dijkstra

minimum spanning tree

Prim   algorithm

Kruskal algorithm

 

shortest path

Plain Dijkstra

Time complexity:          O(n2+m) , n   Represents the number of points, M   Represents the number of sides

Dense graph 👉            Storage form: adjacency matrix

Template:   g[x][y] stores the edge weight during initialization, st[i] indicates whether I is added to the gradually expanding set, dist[i]   What we save is the shortest distance from 1 to I, which is our goal

Idea:

Seek 1   →   n   Shortest path

one   Initialization distance dist[1] = 0,   dist[i] = +∞

2. for  i   1~n:

        for  j  1~n:

                 t   ←   Not in set s,   The point closest to the set

        s   ←   t   (join the organization, i.e. st[t]=true)

        for  j  1~n:

                Use t to update the distance of other points (the distance from the points already in the set to 1 may not be the shortest, and the dist [J] value is updated to   min(dist[j], dist[t] + g[t][j]) )

849. Dijkstra finding the shortest path I - AcWing question bank high quality algorithm question bankhttps://www.acwing.com/problem/content/851/

Input example:

3 3
1 2 2
2 3 1
1 3 4

Output example:

3

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;

const int N = 510;
int n, m;
int dist[N],g[N][N];
bool st[N]; //Whether the tag is in the collection  

int dijkstra()
{
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;
    
    for(int i = 0; i < n; i ++)
    {
        int t = -1;
        for(int j = 1; j <= n; j ++)
            if(!st[j] && (t==-1 || dist[j] < dist[t]))
                t = j;
                
        //if(t == n) break; // You can break in advance to optimize the time overhead 
        
        st[t] = true;
        for(int j = 1; j <= n; j ++)    //Update the shortest path in the collection
            dist[j] = min(dist[j], dist[t]+g[t][j]);
        
    }
    
    if(dist[n] == 0x3f3f3f3f) return -1;
    else return dist[n];
}
int main()
{
    cin >> n >> m;
    
    memset(g, 0x3f, sizeof g);

    int a,b,c;
    for(int i = 0; i < m; i++)
    {
        scanf("%d%d%d", &a, &b, &c);//More edges, scanf saves time
        g[a][b] = min(c, g[a][b]);  //According to the meaning of the question, there may be double edges and self rings in the figure
    }
    
    cout << dijkstra();
}

minimum spanning tree

Prim   algorithm

(very similar to Dijkstra's idea, there is only difference when updating dist, the former is the point with the smallest distance from the set, and the latter is the point with the smallest distance from the starting point)

Idea:

one   Initialization distance   dist[i] = +∞

2. for  i   1~n:

        for  j  1~n:

                 t   ←   Not in set s,   The point closest to the set

        If I= 1 (i.e. not the point at the initial time) and dist[t] = = + ∞ (the graph is not connected),   Exit directly (supplement: as long as it is not the first point, dist[t] represents the length between the current point and a point in the connected set)

        for  j  1~n:

                Use t to update the distance of other points (the distance from the points already in the set to 1 may not be the shortest, and the dist [J] value is updated to   min(dist[j], g[t][j]) (supplement: min(dist[j], g[t][j]), dist [J] indicates that when point t is not added to the set before   Distance from point J to set, g[t][j]   Indicates if the point t is added to the set   Distance from point J to set)

Input example:

4 5
1 2 1
1 3 2
1 4 3
2 3 2
3 4 4

Output example:

6

 

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;

const int N = 510, INF = 0x3f3f3f3f;
int n,m;
int g[N][N],dist[N];
bool st[N];

int prim()
{
    memset(dist, INF, sizeof dist);
    int res = 0;    //Sum of weights of minimum spanning tree
    for(int i = 0; i < n; i++)
    {
        int t = -1;
        for(int j = 1; j <= n; j++)
            if(!st[j] && (t == -1 || dist[j] < dist[t]))
                t = j;
                
        if(i && dist[t]==INF) return INF;
        if(i) res += dist[t];//★ add before updating, otherwise the weight of self ring may be included
        
        for(int j = 1; j <= n; j++)
            dist[j] = min(dist[j], g[t][j]);//★
        
        st[t] = true;//★
    }
    return res;
}

int main()
{
    cin >> n >> m;
    
    memset(g, INF, sizeof g);
    
    int a, b, c;
    while (m -- )
    {
        scanf("%d%d%d", &a, &b, &c);
        g[a][b] = g[b][a] = min(c, g[a][b]); //★
    }
    
    int res = prim();
    if(res == INF) cout << "impossible";
    else cout << res;
    return 0;
}

Kruskal algorithm

(in essence, it is a joint query set)

Idea:

one   All edges are sorted by weight from small to large

two   Enumerate each edge ab,   Weight c

        If a and B are not connected, add this edge to the set

Input example:

4 5
1 2 1
1 3 2
1 4 3
2 3 2
3 4 4

Output example:

6

 

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 100010, M = 200010, INF = 0x3f3f3f3f;

int n, m;
int p[N];

struct Edge{
    int a, b, w;
    bool operator< (const Edge &W)const
    {
        return w < W.w;
    }
}edges[M];

int find(int x)    //Joint search set (compressed path)
{
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

int kruskal()
{
    sort(edges, edges + m);

    for (int i = 1; i <= n; i ++ ) p[i] = i;    // Initialize and query set

    int res = 0, cnt = 0;
    for (int i = 0; i < m; i ++ ){
        int a = edges[i].a, b = edges[i].b, w = edges[i].w;

        a = find(a), b = find(b);
        if (a != b){
            p[a] = b;
            res += w;
            cnt ++ ;
        }
    }

    if (cnt < n-1) return INF;
    else return res;
}

int main()
{
    cin >> n >> m;
    for (int i = 0; i < m; i ++ )
    {
        int a, b, w;
        scanf("%d%d%d", &a, &b, &w);
        edges[i] = {a, b, w};
    }

    int t = kruskal();

    if (t == INF) cout << "impossible";
    else cout << t;

    return 0;
}