Greedy Algorithm
Algorithm principle
Greedy algorithm also belongs to A heuristic algorithm. Greedy algorithm never pays attention to the whole, but always selects the optimal solution based on the current state. Greedy can be regarded as A special case of A *
In the previous blog, we already know that the comprehensive priority of A * algorithm is f(N)=g(N)+h(N). Here, we only need to make g(N)=0, f(N) is the estimated cost in the current state, and only need to select the path with the smallest h(N) each time, which is the optimal solution in the current state
Maze problem
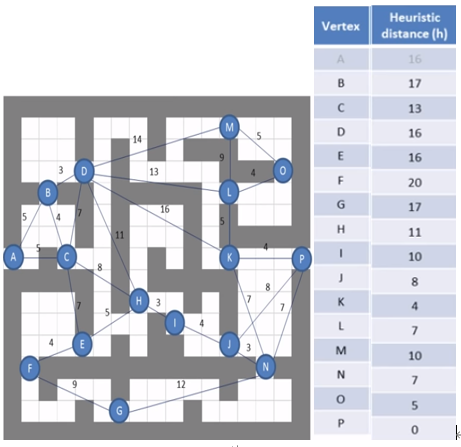
The greedy algorithm never pays attention to g(N), so it only needs to compare h(N) in adjacent nodes every time
The path obtained by greedy algorithm is A-C-H-I-J-P
Backtracking algorithm
Algorithm principle
Backtracking algorithm is an extension of DFS. On the basis of DFS, pruning functions are added. Pruning functions include constraint functions and bound functions to judge whether the current node meets the meaning of the problem. If not, the original path returns. Due to more judgment, fewer nodes are traversed and faster than DFS
Usually, the solution of the problem can be transformed into a multi tree. When a node meets the meaning of the problem, it will continue to traverse its subtree, otherwise it will directly skip the current node
Constraint function
Constraint functions are used to rule out situations where solutions are impossible. For example, in the four queens problem, queens are placed at positions (0,0) and (2,1) respectively. At this time, only positions (1,3) remain on the whole chessboard

Obviously, this situation does not meet the meaning of the question, so skip the node corresponding to this situation
bounding function
The bound function is used to exclude the non optimal solution. For example, in path planning, a path with a length of 10 has been found, and the g(N) of the current node is greater than 10, then there can be no path shorter than 10 in the subtree of the current node, so skip the node
n-queen problem
Problem description
Put n queens in n × On the square paper of N, so that the N queens are not in the same row and column, and are on the same diagonal. All pendulum methods are given
State definition
Define a one-dimensional array queen[n] to represent the Queen's position. queen[i]=j means that the queen in row I is in column j. if j=-1, it means that there is no queen in row I (there is no queen at present, but there will be one in the end)
for example
queen[] = {2,0,3,1} indicates that the Queen's position is as follows

Conflict detection
Obviously, using one-dimensional array representation, it is impossible for queens to be in the same row, so you only need to compare columns and diagonals
//Check whether there are conflicts in the current state
bool CheckConflict() {
for (int i = 0; i < N; i++) {
//queen[i] == -1 indicates that the queen has not been placed
if(queen[i] == -1) continue;
for (int j = i + 1; j < N; j++) {
//queen[j] == -1 indicates that the queen has not been placed
if(queen[j] == -1) continue;
//The queens in row i and row j are in the same column
if (queen[i] == queen[j]) return false;
//Diagonal conflict
if (abs(i - j) == abs(queen[i] - queen[j])) return false;
}
}
return true;
}Constraint function
The constraint function CheckEnable(int i,int j) is used to determine whether the queen can be placed at (i,j). If not, it does not need to continue traversal
//Constraint function to check whether the queen can be placed in (i,j) in the current state
bool CheckEnable(int i, int j) {
queen[i] = j;//Suppose there is a queen on (i,j)
bool flag = CheckConflict();//Judge whether there is conflict
queen[i] = -1;//Restitution
return flag;
}to flash back
//Find the Queen's position on line i
void Search(int i) {
if(i >= N){
num++;
Print();
return;
}
//Traverse all cases of (i,j)
for(int j=0;j<N;j++){
//Judge whether (i,j) can place the queen
if(CheckEnable(i,j)){
//Can be placed, try putting the queen in (i,j)
queen[i] = j;
//Find the play of line i+1
Search(i+1);
//Take the queen
queen[i] = -1;
}
}
}Complete code
#include <iostream>
#include <queue>
using namespace std;
#define N 4
//Array indicates that the queen is unknown, queen[i] indicates which column the queen in row I is in, and - 1 indicates that it is not placed
int queen[N];
//Total number of Solutions
int num = 0;
void Print();
void Search(int i);
int main() {
for (int &i: queen) {
i = -1;
}
Search(0);
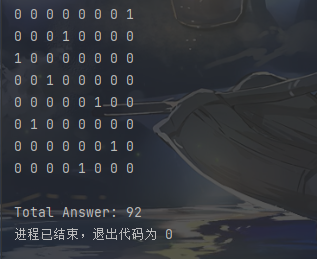
printf("Total Answer: %d",num);
return 0;
}
//Check whether there are conflicts in the current state
bool CheckConflict() {
for (int i = 0; i < N; i++) {
//queen[i] == -1 indicates that the queen has not been placed
if(queen[i] == -1) continue;
for (int j = i + 1; j < N; j++) {
//queen[j] == -1 indicates that the queen has not been placed
if(queen[j] == -1) continue;
//The queens in row i and row j are in the same column
if (queen[i] == queen[j]) return false;
//Diagonal conflict
if (abs(i - j) == abs(queen[i] - queen[j])) return false;
}
}
return true;
}
//Constraint function to check whether the queen can be placed in (i,j) in the current state
bool CheckEnable(int i, int j) {
queen[i] = j;//Suppose there is a queen on (i,j)
bool flag = CheckConflict();//Judge whether there is conflict
queen[i] = -1;//Restitution
return flag;
}
//Traverse the Queen's position on line i
void Search(int i) {
if(i >= N){
num++;
Print();
return;
}
//Traverse all cases of (i,j)
for(int j=0;j<N;j++){
//Judge whether (i,j) can place the queen
if(CheckEnable(i,j)){
//Can be placed, try putting the queen in (i,j)
queen[i] = j;
//Find the play of line i+1
Search(i+1);
//Take the queen
queen[i] = -1;
}
}
}
void Print(){
for(int i : queen){
for(int j=0;j<N;j++){
if(i == j){
printf("1 ");
} else{
printf("0 ");
}
}
printf("\n");
}
printf("\n");
}
When n = 4

When n = 8