⭐ Recursively find the factorial of N

Idea:
This problem is mainly to find the recursive formula. The recursive formula of factorial is still very easy to find, which is obvious
The recursive formula is n × (n-1)!
The termination condition is n==1

Illustration:

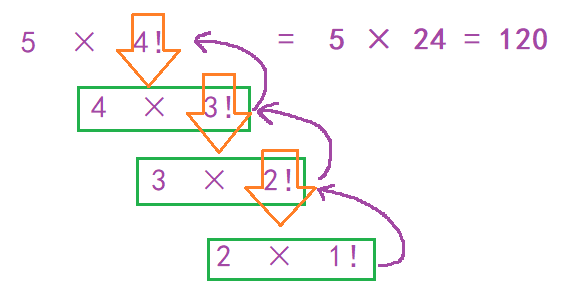
Code implementation:

public class Recursive solution N factorial  {
 public static int JieCheng(int n) {
       if (n==1)  //Termination conditions
        return 1;
      return n * JieCheng(n-1); //Downward recursion
   }
  public static void main(String[] args) {
       int n = 5;
       System.out.println(JieCheng(n));
   }
}

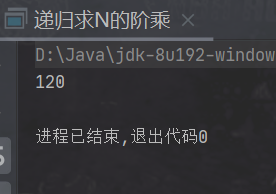
Operation results:
Code implementation: factorial of 5

⭐ Recursively add 1 to 10

Idea:
Starting from 10, 10 + 9 + 8 + 7... + 2 + 1, here is still the same as the previous question. Find the recursive formula dolly, which is equivalent to that the sum of 1 ~ 10 is equal to 10 + (the sum of 1 ~ 9), and the sum of 1 ~ 9 is equal to 9 + (the sum of 1 ~ 8) until 1, and return 1
Recursive formula: n + Add(n-1)
Termination condition: n == 1

Illustration:

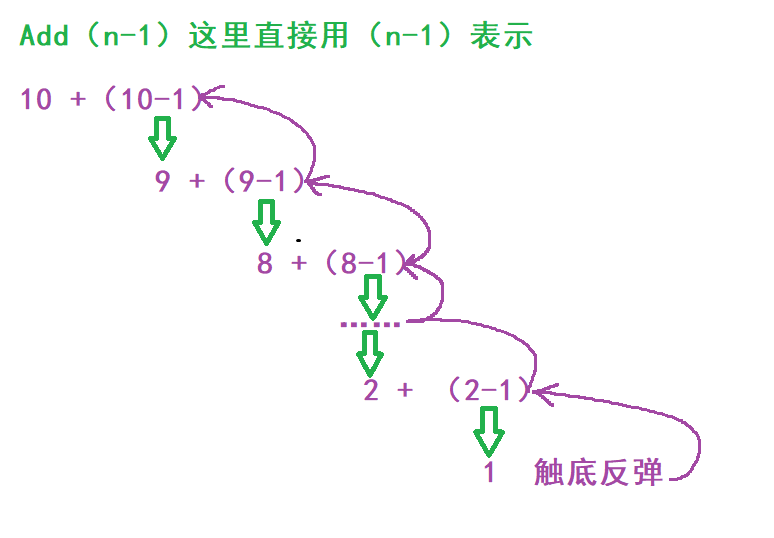
Code implementation:

public class Recursively add 1 to 10 {
 public static int  Add(int n) {
     if (n==1)
         return 1;
     return n + Add(n-1);
   }
   public static void main(String[] args) {
      int n = 10;
     System.out.println(Add(n));
  }
}

Operation results:

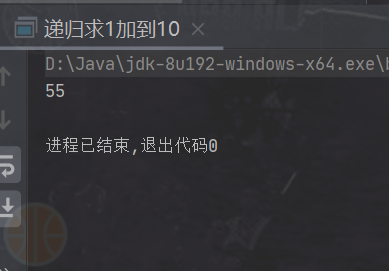
⭐ Recursively returns a nonnegative integer that makes up the sum of its numbers

Idea:
It's still a set of dolls. Use [% 10] to find the number on each bit, use [/ 10] to enter the next call, repeat [% 10] to find the number on the next bit, add it, and return to sum after touching the bottom
Recursive formula: n + AddSum(n/10)
Termination condition: n < 10

Illustration:

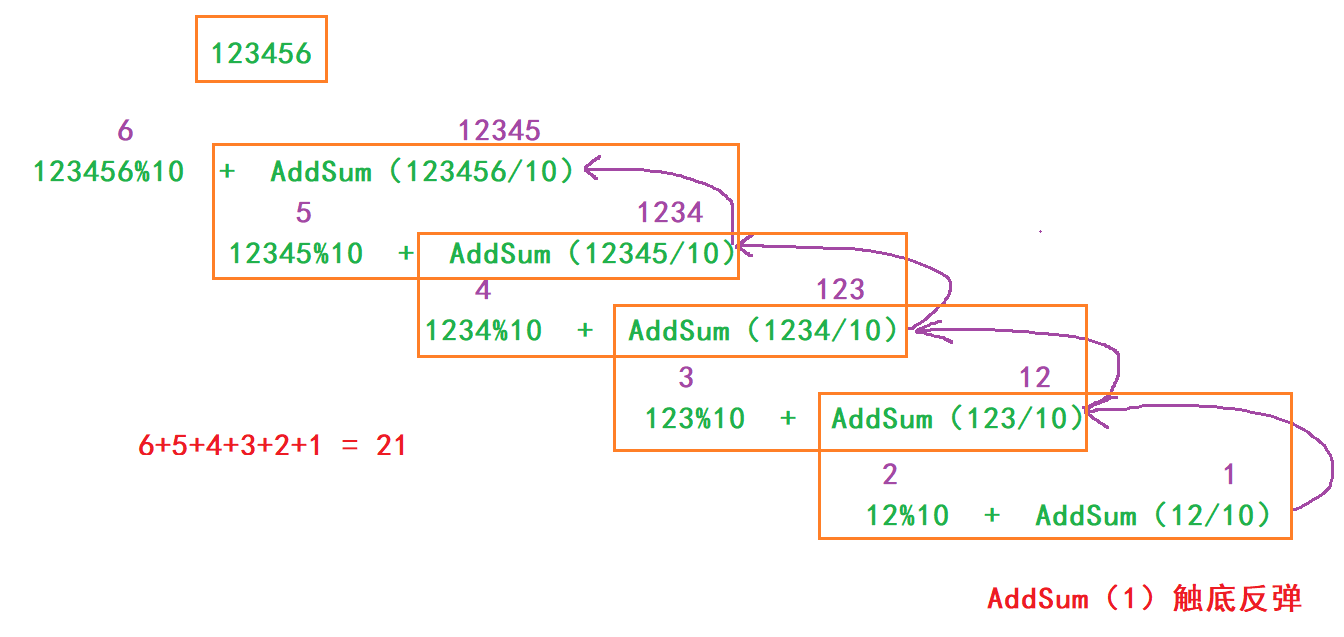
Code implementation:

import java.util.Scanner;
public class Recursively returns a nonnegative integer that makes up the sum of its numbers {
   public static int AddSum(int n) {
       if (n<10)
          return n;
      return (n%10) + AddSum(n/10);
   }
 public static void main(String[] args) {
       Scanner scn = new Scanner(System.in);
     int n = scn.nextInt();
     System.out.println (AddSum(n));
 }
}

Operation results:

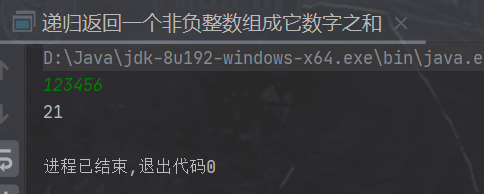
⭐ Print each digit of a number in order

Idea:
The difficulty of this problem is that it needs to print each bit in order. You have to first [/ 10] recurse to its highest layer, then [% 10] print the number on this bit, and then return to the previous layer, print the number on the penultimate bit, and return to the first layer in turn, that is, the layer that prints the number on a bit
Recursive formula: n/10
Termination condition: n < 9

Illustration:

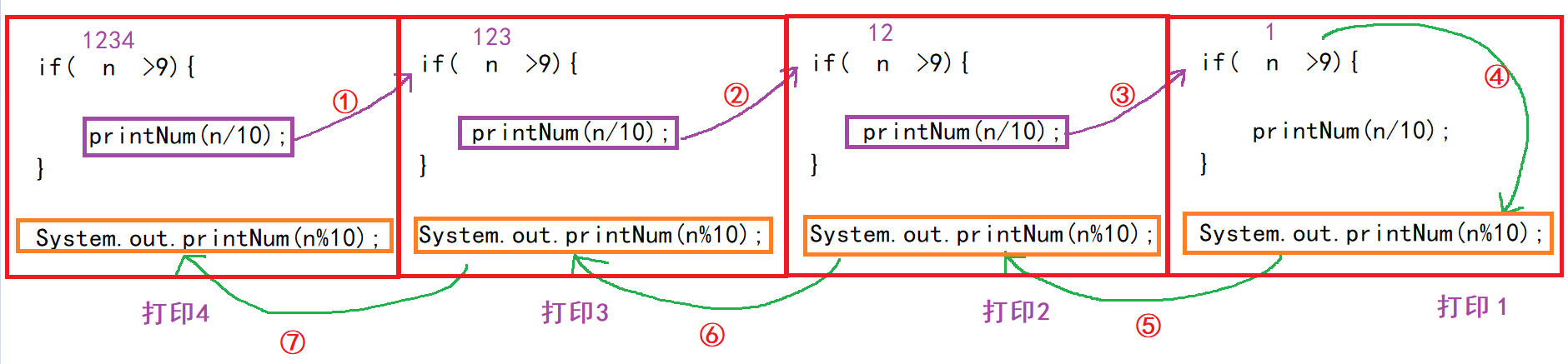
Code implementation:

public class Print each digit of a number in order {
   public static void printNum (int n) {
       if(n > 9){
           printNum(n / 10);
       }
       System.out.println(n % 10);
       //Recursion first, then printing from back to front
   }
   public static void main(String[] args) {
       int n = 12345;
       printNum(n);
 }
}

Operation results:

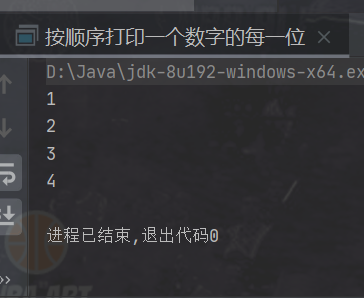
⭐ Recursively find the nth item of Fibonacci sequence [time complexity O(2^N), space complexity O(n)]

Idea:
Fibonacci sequence is a classic recursion problem. There are many methods. Here we mainly talk about recursion. Ordinary recursion is easy to think. The first two items are added to get the third item. It's so simple, but this recursion time is too complex. This method is not recommended, but it can help you learn and understand the meaning of recursion
Recursive formula: Fib (n) = Fib(n-1) + Fib(n-2)
Termination condition: n = = 1 | n = = 2 | n = = 3

Illustration:

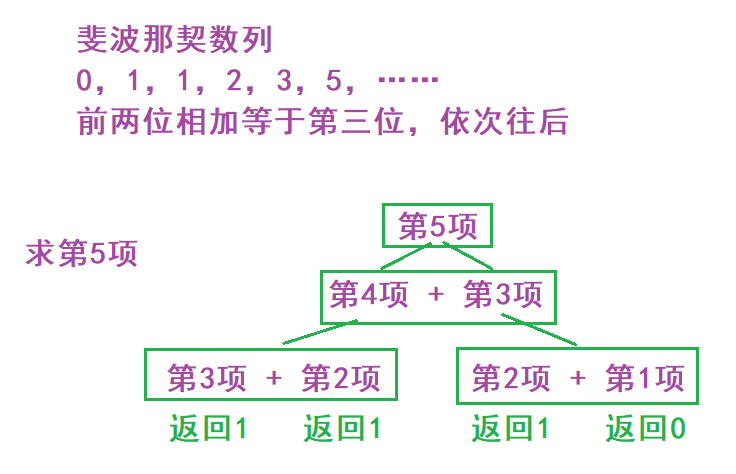
Code implementation:

import java.util.Scanner;

public class Recursively find the second order of Fibonacci sequence N term {//Time complexity O(2^N), space complexity O(n)
   public static int Fib(int n) {
       if (n==1)
           return 0;
      else if (n==2||n==3)
          return 1;
    return Fib(n-1) + Fib(n-2);
   }
 
   public static void main(String[] args) {
       Scanner scn = new Scanner(System.in);
       int n = scn.nextInt();
     System.out.println ("The first"+n+"The Fibonacci number is"+Fib(n));
   }
}

Operation results:

⭐ Efficient recursive Fibonacci sequence [time complexity O(n), space complexity O(1)]

Idea:
If the former recursive solution is calculated from back to front, then this solution is calculated from front to back. This recursive method belongs to tail recursion. Therefore, during recursion, the function will only use the stack space opened by the first stack pressing to cycle in one stack space without opening up other stack spaces. Therefore, the time complexity of this method is O(N) and the space complexity is O(1), Is a very efficient recursive method.
Recursive formula: FIB (SEC, first + sec, n-1);
Termination condition: n == 1

Code implementation:

import java.util.Scanner;

public class Efficient recursive calculation of Fibonacci sequence { //Time complexity O(n), space complexity O(1)
   public static int Fib(int first,int sec,int n) {
     if (n==1)
         return first;
      else
           return Fib(sec,first+sec,n-1);
   }

   public static void main(String[] args) {
       Scanner scn = new Scanner(System.in);
          int n = scn.nextInt();
           System.out.println("The first"+n+"The Fibonacci number is"+Fib(0,1,n));
   }
}

🌟🌟🌟 Solving Hanoi Tower problem

Question introduction:
It is said that in ancient Indian holy temples, there was A game called Hanoi. The game is on A copper plate device with three rods (numbered A, B and C). 64 gold plates are placed in order from bottom to top and from large to small in rod A (as shown in the figure below). The goal of the game: move all the gold plates on pole A to pole C, and keep the original order. Operating rules: only one plate can be moved at A time, and the large plate is always under the three rods and the small plate is on the top. During the operation, the plate can be placed on any rod A, B and C.

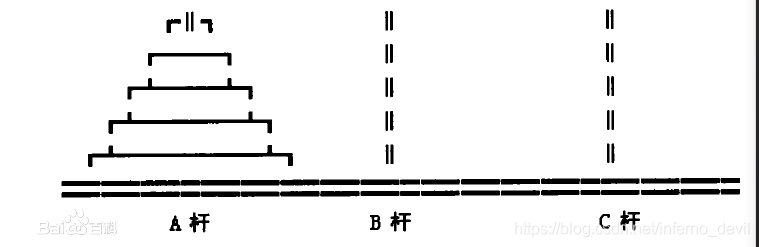
Idea:
For such a problem, no one can write every step of moving the plate directly, but we can use the following methods to solve it.
Set the number of moving plates as n. in order to move these n plates from rod A to rod C, you can do the following three steps:
(1) With Disk C as the intermediary, move disks 1 to n-1 from rod A to rod B;
(2) Move the remaining plate n in rod A to rod C;
(3) Take rod A as the intermediary; Move plates 1 to n-1 from rod B to rod C.
In practice, only the second step can be completed directly, and the first and third steps have become new mobile problems. The essence of the above operation is to transform the problem of moving n plates into moving n-1 plates. In fact, the above method sets the number of plates as N, and N can be any number. This method is also applicable to moving n-1 plates. Therefore, according to the above method, the problem of n -1 plates moving from rod A to rod B (the first step) or from rod B to rod C (the third step) can be solved. Now, the problem is to move n plates
The operation of is transformed into the operation of moving n-2 plates. According to this principle, the original problem can be transformed into the operation of moving n -2, n -3... 3, 2 until moving one disk, and the operation of moving one disk can be completed directly.
Recursive formula:
hanoi(n - 1, start, end, tmp);
Solve the Hanoi Tower problem. move(n, start, end);
hanoi(n - 1, tmp,start , end);
Termination conditions:
There is only one plate left, that is, n==1

Train of thought diagram:

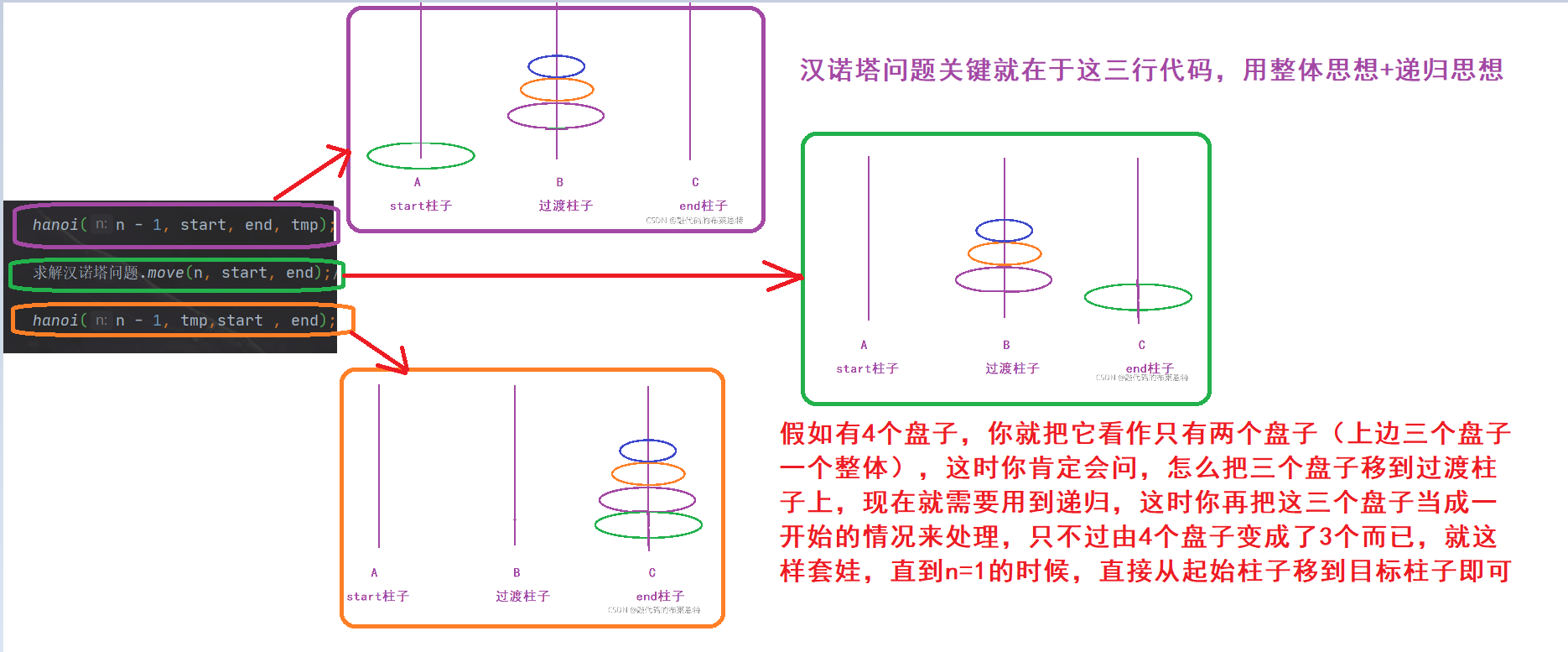
Code implementation: the comments are very detailed, please review them carefully

   import java.util.Scanner;

   public class Solving Hanoi Tower problem {

       static int count = 0;// Number of tag moves

       // Functions that implement movement

      public static void move(int disks, char start, char end) {
           //Number the plates from small to large. Each time, move the plates numbered disks from the start column to the end column
           System.out.println("The first" + (++count) + " Secondary movement : " + " hold " + disks + " No. 1 disc from " + start + " ->Move to->  " + end );
       }

       // Recursive implementation of Hanoi tower function
                     //Incoming data n a B C
       public static void hanoi(int n, char start , char tmp, char end) { //start is the starting tower, tmp is the transition tower, and end is the terminal tower

          if (n == 1)// When there is only one disk, just move it from tower A to tower C

               Solving Hanoi Tower problem.move(1, start, end);// Move disk No. 1 from tower A to tower C

           else

           {
               // otherwise

               hanoi(n - 1, start, end, tmp);// Recursion, move the disk numbered 1~n-1 on tower A to Tower B, and take C as the transition tower

               Solving Hanoi Tower problem.move(n, start, end);// Move the disc numbered n on tower A to tower C

               hanoi(n - 1, tmp,start , end);// Recursion, move the disk numbered 1~n-1 on Tower B to tower C, and take tower A as the transition tower

           }
       }

       public static void main(String[] args) {
           Scanner in = new Scanner(System.in);

           char A = 'A';

           char B = 'B';

           char C = 'C';
           System.out.print("Please enter the number of discs:");
          int n = in.nextInt();
          Solving Hanoi Tower problem.hanoi(n, A, B, C);
          System.out.println(">>Moved" + count + "Time, put A The disks on the have moved to C upper");
         in.close();
     }

   }

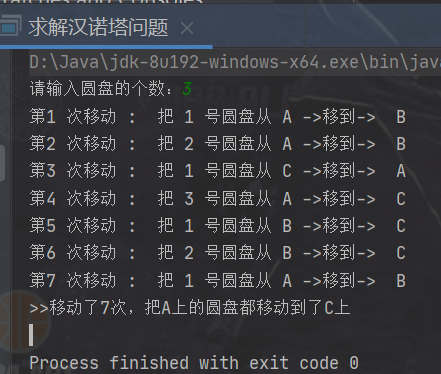
Operation results:

🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙
        ❤ Originality is not easy. If there is any error, please leave a message in the comment area. Thank you very much ❤
        ❤                 If you think the content is good, it's not too much to give a three company~        ❤
        ❤                              I'll pay a return visit when I see it~                                       ❤
🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙