Write before:
Children's shoes that only need code Slide to the end That is;
Children's shoes that need to learn from ideas Part IV That is;
Want to figure out a few concepts of children's shoes Part III That's it.

1, Experimental purpose

The LL (1) analysis program is compiled and debugged according to a grammar to analyze any input symbol string. The purpose of this experiment is to deepen the understanding of prediction analysis LL (1) analysis method.

2, Experimental requirements

1. Manually enter Grammar (read from file)
2. Displays the First set of non terminators for the grammar
3. Displays the Follow set of non terminators for the grammar
4. Displays the Select collection of rules
5. Structural prediction analysis table
6. Analyze any input symbol string

3, Theoretical basis

3.1 top down analysis and LL(1) analysis

Top down analysis: starting from the start symbol of grammar and according to the current input string, determine what kind of production formula to replace the corresponding non terminator in the next step to deduce downward. (how to construct a syntax tree based on the current input string from the root node)

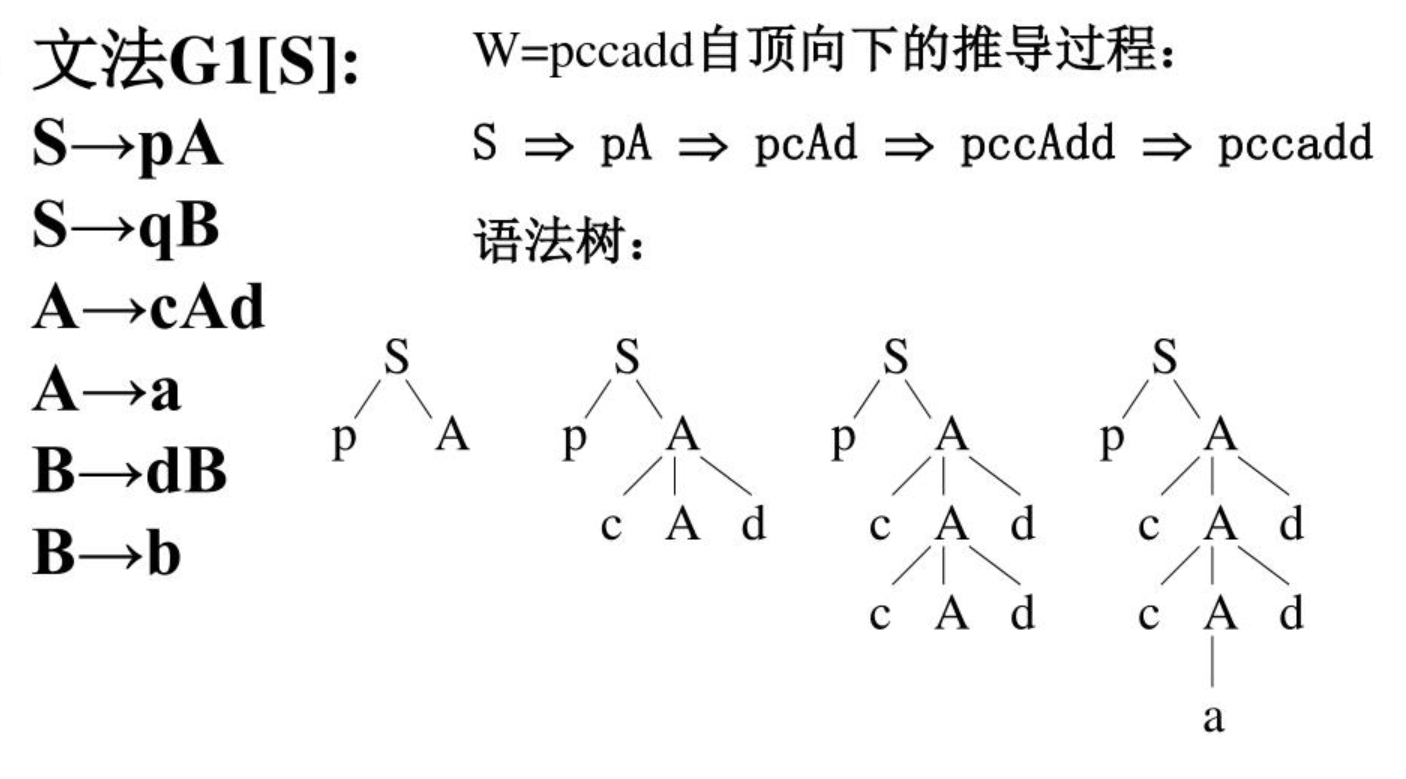
The above figure is the syntax tree derived from the top-down analysis according to the input string W starting from the start symbol S

LL (1) analysis is a top-down syntax analysis method, which means:
The first L: scan the input string from left to right;
The second L: the leftmost derivation is used in the analysis process;
1 in parentheses: you only need to look to the right for one character to determine how to deduce.

3.2 start symbol set First

Definition: first( β) yes β All possible derivations of start and end characters or possible є

First(β)=｛a︱β -> ay,a∈Vt,y∈V* }

Meaning: if there are multiple productions for the same non terminator, it can be uniquely determined according to the first set to the right of which production the input symbol belongs. (the first set does not intersect)

3.3 symbol set Follow

Definition: Follow(U) is a collection of terminators or in all sentence patterns containing u immediately following U.

FOLLOW(A)＝{ a | S... Aa ...，a∈VT }

Meaning: if there are multiple productions for the same non terminator, if the right part is empty, it can also be uniquely determined according to the follow set to the left of which production the input symbol belongs. (the follow sets do not intersect)

3.4 optional symbol set

Definition: the set of input symbols that can be derived from this production formula.

Select(A→β)= 
(1)First(β)，WhenβNot empty symbol string
(2)Follow(A)，WhenβEmpty symbol string

Meaning: for example, the above formula means First( β) Or elements in the Follow (A) set, you can use A → β This production is derived.

Used to determine: the production must be uniquely determined before it can be successfully deduced, so the select set of the production starting with the same non terminator cannot have intersection.

3.5 forecast analysis table

Definition: according to the top elements of the analysis stack and the current input string characters, a production can be uniquely determined. All possible situations can be summarized into a table, which is the prediction analysis table.
The lattice that cannot be deduced is written as ERR. When analyzing the input string, you only need to query this table. The above non terminator sets are the basis for building this table.

4, Experimental steps

4.1 solve start symbol set First

General idea:

• 1. If X ∈ Vt, FIrst (X) = X;
• 2. If x ∈ Vn, X → a..., FIrst (x) = a;
• 3. If x ∈ Vn, X → ε， be ε ∈FIrst(X)
• 4. If x ∈ Vn, X → Y 1 Y_1 Y1​ Y 2 Y_2 Y2​ Y 3 Y_3 Y3​，
• • If Y 1 Y_1 Y1​， Y 2 Y_2 Y2​→ ε， Then FIrst( Y 1 Y_1 Y1​)∪FIrst( Y 2 Y_2 Y2​)-{ε}∈FIrst(X)
• • If Y 1 Y_1 Y1​， Y 2 Y_2 Y2​， Y 3 Y_3 Y3​→ ε， Then FIrst( Y 1 Y_1 Y1​)∪FIrst( Y 2 Y_2 Y2​)∪FIrst( Y 3 Y_3 Y3​)∪{ε}∈FIrst(X)
• • Y more, and so on
• 5. Repeat the above steps until the First set no longer grows

Solution idea: Taking vn as an example

Traverse the non terminator set of grammar, solve it one by one, and insert the result into the FIRST set.

The results are stored using a set < char >.
The FIRST set is stored in an unordered_map hash table. The key is a non terminator and the value is the result obtained.

• Solve one by one:
• 1. Get all the right parts of vn for analysis
• 2. Traverse the right part, analyze the right part one by one, solve the first set respectively, and add it to the results
• • 2.1 traverse the current right part (character analysis)
• • • If the first character is a terminator, add the first set and jump out of the loop; (extra null characters will be added here)
• • • If it is a non terminator, it is processed recursively;
• • • If the non terminator can be pushed empty, it is also necessary to cycle the next character (if any) in the right part
• 3. At the end of the traversal, if the character cannot be pushed empty, delete the null character in results and return result

Flow chart: generally as follows, see the code for detailed implementation.

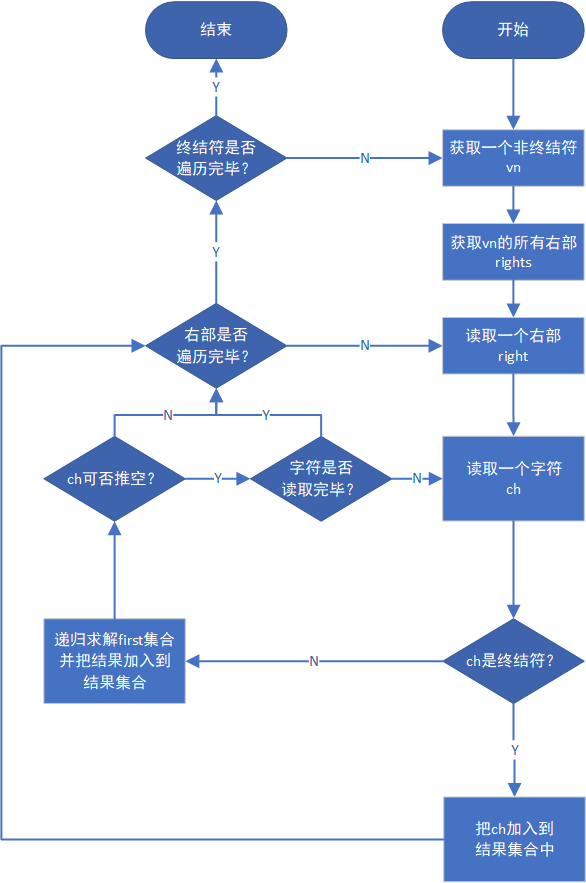
4.2 solving followed by symbol set Follow

General idea:

• 1. If X is the start symbol, # ∈ Follow(X);
• 2. If A → α X β， Then first( β) - { ε} ∈ Follow(X); if β Can be empty, Follow(A) ∈ Follow(X)
• 3. Repeat the above steps until the Follow set is no longer growing

Solution idea:

Traverse the non terminator set of grammar, solve it one by one, insert the result into the follow set, and then improve the follow set until the follow set is no longer increased.

The results are stored using a set.
The FOLLOW set is also stored in an unordered_map hash table. The key is a non terminator and the value is the result of the evaluation.

• Solve one by one:
• 1. For the start symbol, add # to results
• 2. Traverse all right expressions of the current grammar,
• 1. Traverse the current right part for analysis. If vn is found, proceed to the next step to obtain the results element
• 1. If the current character vn is the last character, indicating that it is at the end of the sentence, add # it; otherwise, traverse the characters after vn
• 1. If the terminator is encountered, it is directly added to the results and break to exit the loop
• 1. Otherwise, if it is a non terminator, find its first set, remove the null and add it to the results. At this time, consider whether to continue the loop or jump out of the loop:
     If the current character can be pushed empty and is not the last character, it means that the next character needs to be analyzed
     If it can be pushed empty but is the last character, add # results
     If you can't push null, just jump out of the loop (if you can push null, the first set of the following characters can be used as the follow set of vn)
• 3. After traversal, results are returned;
• 4. Improve the follow set: for all non terminators, if there is no character or a character that can be pushed empty, add the follow set on the left to the result set.
• 5. Repeat step 4 until the follow set is no longer large. (when using recursion in this place, the right recursion of the grammar will fall into an endless loop, so do it first, regardless of idea 2 β In the case of empty pushing, solve the follow for the first time, and then take it into account in the process of perfecting the follow set)

flow chart

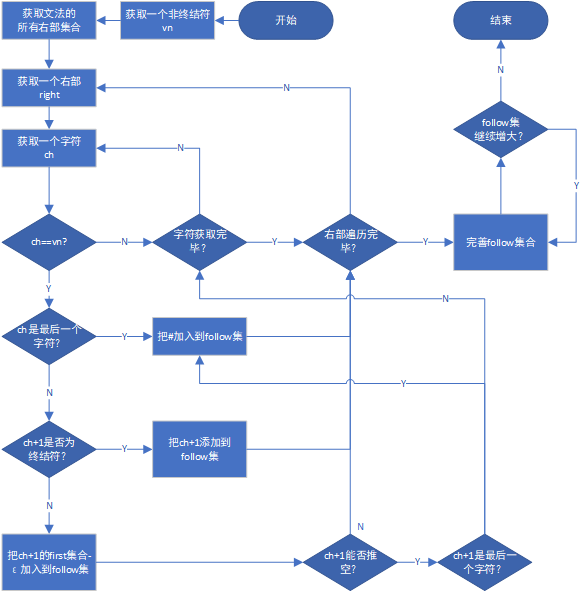
Improve the flow chart of Follow collection

4.3 solving optional symbol sets

General idea

For A production formula: A → β

• If β Can not be empty, select(A → β) = first( β)
• If β select(A → β) = (first( β)- { ε}) ∪follow(A)

Solution idea

1. Get the left and right of the production
2. Traversing the right production, first analyze the first character in the right: right[0]
   2.1 if it is a Terminator: (if it is empty, add follow(left) to results, otherwise directly add the symbol to results), and then break
   2.2 if it is a non Terminator: add first(right[0]) - '~' to results; If you can still push empty, continue to look back. If it is the last character, add follow(left) to results

flow chart

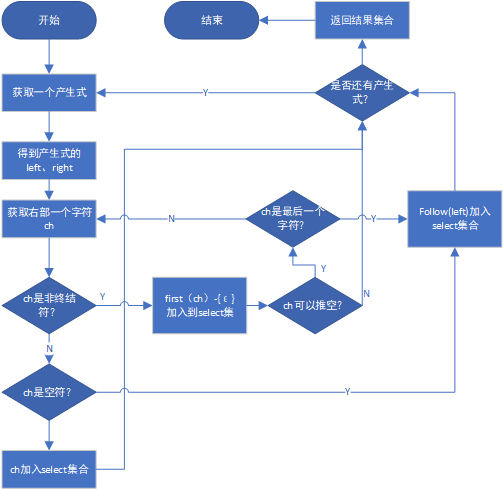
4.4 solution prediction analysis table

General idea

Select (a → BC) = {a, b, c} indicates:
When the top element of the stack is a, if the current character of the input string is a or b or c, it can be determined to select a → BC for derivation.
The prediction analysis table is obtained by traversing all select ions and storing all situations one by one.

Solution idea

1. Traverse the select collection
2. Get left and - > right; And the corresponding terminator set chars
3. Traverse chars to get a single character ch:
   Pair left and ch as the key of TABLE, and - > right as the value

flow chart

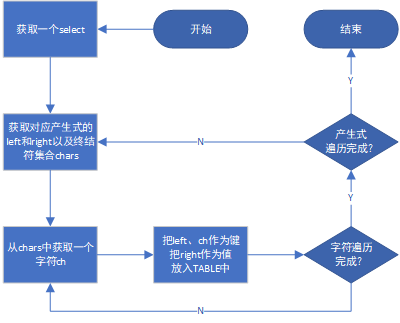
4.5 solution analysis input string

General idea

1. First, put # and the start character S into the analysis stack, set the character ch of the input string, and enter the analysis. In the process:
2. Analyze the stack top element X. if it is the same terminator as ch, it indicates that the matching is successful. Otherwise, it depends on whether it can be deduced (check whether there is anything in the prediction analysis table). If it can be deduced, the production is put on the stack in reverse order, otherwise the grammar cannot accept the string and the analysis is completed.
3. Finally, if the analysis stack and the input string are all left #, the matching is successful, and the current grammar accepts the string.

Solution idea

1. Build first in and then out of the stack, and put #, S into the stack
2. Traverse the sentences and send symbols to a; And stack push X to enter the analysis

• 2.1 if X is a terminator
  If it is equal to a, the match is successful: X is out of the stack and reads the next character;
  Otherwise, it cannot be matched: fail to exit
• 2.2 if X is the end character
  a is also the end character and accepts the analysis string: exit successfully
  a is not the end character. It does not accept the analysis string. Exit after failure
• 2.3 otherwise, X is a non terminator
  Look up the prediction analysis table to see if there is an expression
  If not, the analysis will fail and exit
  If yes, the X element goes out of the stack and the expression goes into the stack in reverse order. Continue to cycle the sentence and analyze a repeatedly

1. The traversal is completed and the program ends

flow chart

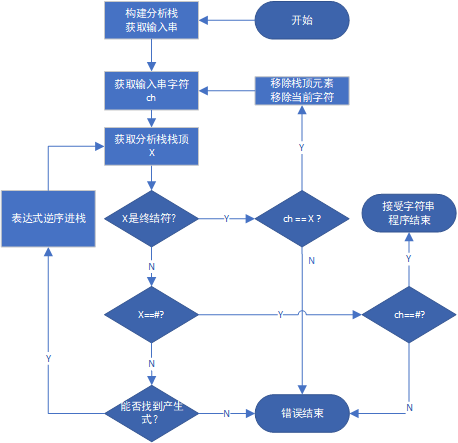
4.6 operation results

Grammar grammar.txt:

E->TG
G->+TG
G->~
T->FS
S->*FS
S->~
F->(E)
F->i

Input string:

i*(i+i)

Result diagram:

5, Experimental code

#include <iostream>
#include <iomanip>
#include <stdio.h>
#Include < fsstream > / / file stream
#Include < string > / / String
#Include < algorithm > / / string processing
#include <unordered_ Map > / / hash table
#Include < Map > / / figure
#Include < stack > / / stack
#Include < set > / / set
#Include < vector > / / vector
using namespace std;

// Main global variable definitions
unordered_map<string,string> grammar;// Grammar set hash table
string S; // Start character
set<string> Vn; // Non terminator set
set<string> Vt; // Terminator set
set<string> formulas; // Production set. It is convenient to traverse when solving select
unordered_map<string, set<char>> FIRST;// FIRST set
unordered_map<string, set<char>> FOLLOW;// FOLLOW set
unordered_map<string, set<char>> SELECT;// Select set
map<pair<char,char>, string> TABLE;// Forecast analysis table


//							Function predefined
//					Function function
void readFile();	 // read file
void pretreatment(); // Preprocessing, simplification, symbol classification, etc

set<char> findFirstBV(string vn); // First set of a non Terminator (recursive solution)
void findFirst();				  // Use hash table storage

set<char> findFollowBV(string vn); // Follow set of a non Terminator (recursive solution)
void findFollow();                 // Use hash table storage

set<char> findSelectBF(string formula);  // Select set of a production (recursive solution)
void findSelect();                       // Use hash table storage

void isLL1();      // Judge whether it is LL(1) analysis

void makeTable();  // Structural prediction analysis table

void LL1Analyse(); // Parse string

//					Tool function 
// Get the right part (set) of the production according to the left part
vector<string> getRights(string left);
// Determine whether it is a terminator or non terminator
bool isVn(char v);
bool isVt(char v);
// Judge whether a non terminator can push null
bool canToEmpty(char v);
//Judge whether the intersection of two character set s is empty
bool isIntersect(set<char> a, set<char> b);
// Output analysis table
void printTable();
// Get the string in reverse order
string getStackRemain(stack<char> stack_remain);
// Displays and outputs a char set
void printSet(set<char> sets);
// Find the number of elements in the follow set (for judgment: until the follow set no longer increases)
int getFS();


// =====================================Main function===================================
int main() {
	cout <<setw(75)<<right<<setfill('=')<< "LL(1)analyzer====================" << endl << endl;
	// =====================================Enter the core code: LL(1) analysis==================================
	// =====================================1. Reading grammar and simple processing==================================
	readFile();
	// =====================================2. Find First set=============================================
	findFirst();
	// =====================================3. Find Follow set============================================
	findFollow();
	// =====================================4. Select set not found============================================
	findSelect();
	// =====================================5. Determine whether it is LL1 grammar=====================================
	isLL1();
	// =====================================6. Build analysis table============================================
	makeTable();
	// =====================================7. Parse string============================================
	LL1Analyse();
	return 0;
}

// =====================================Function function===================================
// read file
void readFile() {
	// Enter file name
	cout << endl << "Please enter a file name:";
	char file[100];
	cin >> file;
	// Show all the contents of the file first
	cout << endl << setw(75) << right << setfill('=') << "Grammar reading====================" << endl;
	// ifstream file stream open file
	ifstream fin(file);
	if (!fin.is_open())
	{
		cout << "fail to open file";
		exit(-1); // immediate withdrawal
	}
	string line;
	bool isGet = false;
	while (getline(fin, line)) // Read line by line
	{
		if (!isGet)
		{
			// Get start character
			S = line[0];
			isGet = true;
		}
		formulas.insert(line); // Get all expressions
		cout << line << endl;  // output
							  					  
		// If the key already exists in the hash table, add it later
		for (auto iter = grammar.begin(); iter != grammar.end(); ++iter) {
			if (iter->first == string(1, line[0]))
			{
				iter->second = iter->second + "|" + line.substr(3);
				break;
			}
		}
		// Inserts a key value pair into the hash table where the grammar is stored
		grammar.insert(pair<string, string>(string(1, line[0]), line.substr(3)));
	}

	cout << "Please note that~Indicates null" << endl;
	fin.close(); // Close file stream

	pretreatment();
}
// Simple processing: symbol classification, output and display
void pretreatment() {
	cout << endl << setw(75) << right << setfill('=') << "Grammatical simplification====================" << endl;
	// Traversal grammar hash table
	for (auto iter = grammar.begin(); iter != grammar.end(); ++iter) {
		// output
		cout << iter->first << "→" << iter->second << endl;
		// ========================================Symbol classification==================================
		Vn.insert(iter->first); // Non terminator set
		// Terminator set
		string str = iter->second;
		for (size_t i = 0; i < str.length(); i++)
		{
			if (str[i] != '|' && (str[i] < 'A' || str[i] > 'Z'))
			{
				Vt.insert(string(1, str[i]));
			}
		}
	}

	cout << endl << setw(75) << right << setfill('=') << "Symbol classification====================" << endl;
	// Output terminator and non terminator sets
	cout << "Start symbol:" << S << endl;
	cout << "Non terminator set Vn = " << "{";
	for (auto iter = Vn.begin(); iter != Vn.end(); ) {
		cout << *iter;
		if ((++iter) != Vn.end())
		{
			cout << ",";
		}
	}
	cout << "}" << endl;

	cout << "Terminator set Vt = " << "{";
	for (auto iter = Vt.begin(); iter != Vt.end(); ) {
		cout << *iter;
		if ((++iter) != Vt.end())
		{
			cout << ",";
		}
	}
	cout << "}" << endl;
}

//  Find the First set of a non terminator
set<char> findFirstBV(string vn) {
	// Solution idea
		//1. Get the right part of vn for analysis
		//2. Traverse the right part, analyze the right part one by one, solve the first set respectively, and add it to the results
			//2.1 traverse the current right part (character analysis)
				//If the first character is a terminator, add the first set and jump out; (extra null characters will be added here)
				//If it is a non terminator, it is processed recursively;
				//If the non terminator can be pushed empty, it is also necessary to cycle the next character (if any) in the right part
		//3. At the end of the traversal, if the character cannot be pushed empty, delete the empty character in the results; Return results

	set<char> results; // first save set
	vector<string> rights = getRights(vn); // Get right
	if (!rights.empty()) // If the right part is not empty
	{
		// Traverse the right set (each right part solves first separately and adds it to the first set of the non terminator)
		for (auto iter = rights.begin(); iter != rights.end();++iter) {
			string right = *iter;
			// Traverse the current right part: / / if the first character is a terminator, add the first set and jump out of the loop;
						      //If it is a non terminator, it is processed recursively;
								//If the non terminator can be pushed empty, it is also necessary to cycle the next character (if any) in the right part
			for (auto ch = right.begin(); ch != right.end(); ++ch) {
				if (isVn(*ch)) // If it is a non terminator, it needs to be processed recursively
				{
					//Check the first set first. If it already exists, there is no need to solve it repeatedly
					if (FIRST.find(string(1, *ch)) == FIRST.end()) // The fisrt set does not exist
					{
						// Call itself recursively!!!
						set<char> chars = findFirstBV(string(1, *ch));
						// Store results in results
						results.insert(chars.begin(),chars.end());
						FIRST.insert(pair<string,set<char>>(string(1,*ch),chars));
					}
					else { // If it exists, add all the set to first (improve efficiency)
						set<char> chars = FIRST[string(1, *ch)];
						results.insert(chars.begin(), chars.end());
					}

					// If this character can be pushed empty and there are characters after it, the next character needs to be processed
					if (canToEmpty(*ch) && (iter + 1) != rights.end())
					{
						continue;
					}
					else
						break; // Otherwise, directly exit the loop traversing the current right part

				}
				else { // If it is not a non terminator, directly add this character to the first set and jump out
					// In this step, the preceding blank will be added (it will be deleted later)
					results.insert(*ch);
					break;
				}
			}
		}
	}
	// Finally, if the terminator cannot be pushed empty, it is deleted
	if (!canToEmpty(vn[0]))
	{
		results.erase('~');
	}
	return results;
}
// Solve the First set and store it using a hash table
void findFirst() {
	// Traverse the non terminator set and build a hash table for subsequent queries
	for (auto iter = Vn.begin(); iter != Vn.end(); ++iter) {
		string vn = *iter; // Get non Terminator
		set<char> firsts = findFirstBV(vn); // Store the first set of Vn
		FIRST.insert(pair<string, set<char>>(vn, firsts));
	}
	// display output
	cout << endl << setw(75) << right << setfill('=') << "FISRT Set analysis====================" << endl;
	for (auto iter = FIRST.begin(); iter != FIRST.end();++iter) {
		cout <<"FIRST("<< iter->first<<")" << "= ";
		set<char> sets = iter->second;
		printSet(sets);
	}
}

// A single non terminator solves its Follow set
set<char> findFollowBV(string vn) {
	//Solution idea:
		//1. For the start symbol, add # to results
		//2. Traverse all right expressions of the current grammar,
			//2.1 traverse the current right part for analysis. If vn is found, proceed to the next step to obtain the results element
				//If the current character vn is the last character, it indicates that it is at the end of the sentence, then # add
				//Otherwise, the character after traversing vn
					// If vn is encountered again, go back and exit the loop and enter the external loop
					// If the terminator is encountered, it is directly added to the results and break to exit the loop
					// Otherwise, if it is a non terminator, find its first set, remove the null and add it to the results
						// At this time, you should also consider whether to continue the loop or jump out of the loop:
							//If the current character can be pushed empty and is not the last character, it means that the next character needs to be analyzed
							//If it can be pushed empty but is the last character, add # results
							//If you can't push null, just jump out of the loop (if you can push null, the first set of the following characters can be used as the follow set of vn)
		//3. After traversal, results are returned; The specific codes are as follows:
	set<char> results; // Store solution results
	if (vn == S) // If it is the start symbol
	{
		results.insert('#'); // Add the terminator because there is a statement #S#
	}

	// Traverse all right sets of grammars
	for (auto iter = formulas.begin(); iter != formulas.end(); ++iter)
	{
		string right = (*iter).substr(3); // Get current right
		// Traverse the current right to see if it contains the current symbol
		for (auto i_ch = right.begin(); i_ch != right.end();)
		{
			if (*i_ch == vn[0]) { // If vn appears in the current right
				if ((i_ch+1)==right.end()) // vn is the last character on the right of the current
 				{
					results.insert('#'); //  Add Terminator
					break;
				}
				else { // vn is followed by characters. Traverse them (unless vn: i_ch returns one and enters the jump loop again)
					while (i_ch != right.end())
					{
						++i_ch;// Pointer backward
						if (*i_ch == vn[0])
						{
							--i_ch;
							break;
						}
						if (isVn(*i_ch)) // If the character is a non terminator, add the non empty element in the first set
						{
							set<char> tmp_f = FIRST[string(1, *i_ch)];
							tmp_f.erase('~'); // Remove empty
							results.insert(tmp_f.begin(), tmp_f.end());
							

							// Whether the character can be pushed empty or not needs to be considered whether to continue the cycle
							if (canToEmpty(*i_ch))
							{
								if ((i_ch + 1) == right.end()) // If it is the last character, add#
								{
									results.insert('#');
									break;// Jump out of loop
								}
								// Continue the cycle
							}
							else // Otherwise, jump out of the loop
								break;
						}
						else {  // If the character is a terminator
							results.insert(*(i_ch));  // Add this character
							break;  // Jump out of loop
						}
					}
				}
			}
			else {
				++i_ch;
			}
		}
	}
	return results;
}
// Perfect Follow set
void completeFollow(string vn) {
	// Traverse all right sets of grammars
	for (auto iter = formulas.begin(); iter != formulas.end(); ++iter)
	{
		
		string right = (*iter).substr(3); // Get current right
		// Traverse the current right to see if it contains the current symbol
		for (auto i_ch = right.begin(); i_ch != right.end();)
		{
			char vn_tmp = *i_ch;
			if (vn_tmp == vn[0]) { // If vn appears in the current right
				if ((i_ch + 1) == right.end()) // vn is the last character on the right of the current
				{
					char left = (*iter)[0];
					set<char> tmp_fo = FOLLOW[string(1,left)]; // Gets the follow collection on the left
					set<char> follows = FOLLOW[string(1,vn_tmp)]; // Get your original follow collection
					follows.insert(tmp_fo.begin(),tmp_fo.end());
					FOLLOW[vn] = follows; // modify
					break;
				}
				else { // If it is not the last character, you need to traverse the following characters to see if they can be pushed empty
					while (i_ch != right.end())
					{
						++i_ch; // Note that the pointer moves back!!!
						if (canToEmpty(*i_ch))
						{
							if ((i_ch+1)!=right.end()) // If it is not the last element, we should continue to see if there is one that can be pushed empty
							{
								continue;
							}
							else { // If the last one can also be pushed empty, add the left one
								char left = (*iter)[0];
								set<char> tmp_fo = FOLLOW[string(1, left)]; // follow set on the left
								set<char> follows = FOLLOW[string(1, vn_tmp)]; // The follow collection of the current symbol
								follows.insert(tmp_fo.begin(), tmp_fo.end());
								FOLLOW[vn] = follows; // Modify original value
								break;
							}
						}
						else  // If it cannot be pushed empty, exit the loop
							break;
					}
				}
			}
			++i_ch; // Traverse to find if vn appears
		}
	}
}
// Solve the Follow set and store it using a hash table
void findFollow() {
	// Traverse all non terminators and solve the follow set in turn
	for (auto iter = Vn.begin(); iter != Vn.end(); ++iter) {
		string vn = *iter; // Get non Terminator
		set<char> follows = findFollowBV(vn); // Solve a follow set of Vn
		FOLLOW.insert(pair<string, set<char>>(vn, follows)); // Stored in hash table to improve query efficiency
	
	}
	// Refine the follow set until the follow is no longer growing
	int old_count = getFS();
	int new_count = -1;
	while (old_count != new_count) // The terminator is changing. Repeat this process until the follow set is no longer growing
	{
		old_count = getFS();
		// Traverse the non terminator again. If it appears at the end of the right, add the follow set on the left
		for (auto iter = Vn.begin(); iter != Vn.end(); ++iter) {
			string vn = *iter; // Get non Terminator
			completeFollow(vn);
		}
		new_count = getFS();
	}
	// display output
	cout << endl << setw(75) << right << setfill('=') << "FOLLOW Set analysis====================" << endl;
	for (auto iter = FOLLOW.begin(); iter != FOLLOW.end(); ++iter) {
		cout << "FOLLOW(" << iter->first << ")" << "= ";
		set<char> sets = iter->second;
		printSet(sets);
	}
}

// Solving a Select set with a single expression
set<char> findSelectBF(string formula) {
	// Solution idea
		// 1. Get the left and right of the production
		// 2. Traversing the right production, first analyze the first character in the right: right[0]
			// If it is a Terminator: (if it is empty, add follow(left) to results, otherwise directly add the symbol to results), and then break
			// If it is a non Terminator: add first(right[0]) - '~' to results; If you can still push empty, continue to look back
	set<char> results; // Store results
		// 1. Get the left and right of the production
	char left = formula[0]; // Left
	string right = formula.substr(3); // Right part
	//Cout < < select set analysis < < left < - > "< right < < endl// Trial adjustment
		// 2. Traversing the right production, first analyze the first character in the right: right[0]
	for (auto iter = right.begin(); iter != right.end(); ++iter)
	{
		//Cout < < "traverse the right" < * ITER < < endl// Trial adjustment
		// If it is a non Terminator: add first(right[0]) - '~' to results; If you can still push empty, continue to look back
		if (isVn(*iter))
		{
			set<char> chs = FIRST.find(string(1, *iter))->second; // Get the first
			chs.erase('~'); // Remove null
			results.insert(chs.begin(), chs.end()); // Join select
			if (canToEmpty(*iter)) // If you can push empty, continue processing and add the next character to the select set
			{
				if ((iter+1)==right.end()) // If the current character is the last character, add follow(left) to results, and then break
				{
					set<char> chs = FOLLOW.find(string(1, left))->second; // Get the follow on the left
					results.insert(chs.begin(), chs.end()); // Join select
				}
				else { // Continue processing the next character
					continue;
				}
			}else
				break; // This character cannot be pushed empty. Exit the loop
		}
		else {// If it is a Terminator: (if it is empty, add follow(left) to results, otherwise directly add the symbol to results), and then break
			if (*iter == '~') // If empty
			{
				set<char> chs = FOLLOW.find(string(1, left))->second; // Get the follow on the left
				results.insert(chs.begin(), chs.end()); // Join select
			}
			else
				results.insert(*iter); // Add select directly
			break; // Exit loop
		}
	}

	return results;
}
// Solve the Select set and store it using a hash table
void findSelect() {
	// Traversal expression set
	for (auto iter = formulas.begin(); iter != formulas.end(); ++iter) {
		string formula = *iter; // Get expression
		set<char> selects = findSelectBF(formula); // Store the first set of Vn
		SELECT.insert(pair<string, set<char>>(formula, selects));  // Insert into hash table to improve query efficiency
	}

	// display output
	cout << endl << setw(75) << right << setfill('=') << "SELECT Set analysis====================" << endl;
	for (auto iter = SELECT.begin(); iter != SELECT.end(); ++iter) {
		cout << "SELECT(" << iter->first << ")" << "= ";
		set<char> sets = iter->second;
		printSet(sets);
	}
}

// Judge whether it is LL(1) analysis
void isLL1() {
	// Solution idea: through nested loop SELECT sets, judge whether there is intersection between SELECT sets with different expressions but the same left
		// If there is an intersection, it indicates that it is not LL1, otherwise it is LL1 analysis
	for (auto i1 = SELECT.begin(); i1 != SELECT.end(); ++i1)
	{
		for (auto i2 = SELECT.begin(); i2 != SELECT.end(); ++i2)
		{
			char left1 = (i1->first)[0]; // Get left 2
			char left2 = (i2->first)[0]; // Get left 2
			if (left1 == left2) // Left equal
			{
				if (i1->first != i2->first) //Different expressions
				{
					if (isIntersect(i1->second, i2->second)) { // If the select set has an intersection
						// Not LL1 grammar
						cout << "After analysis, the grammar you entered does not match LL(1)Grammar, please modify it and try again" << endl;
						exit(0); // immediate withdrawal
					}
				}
			}
		}
	}
	// Is LL (1) grammar
	cout << setw(75) << right << setfill('=') << "Enter analyzer====================" << endl << endl;
	cout << "After analysis, the grammar you entered meets the requirements LL(1)Grammar..." << endl;
}

// Structural prediction analysis table
void makeTable() {
	cout << "Constructing analysis table for you..." << endl;
	// Solution idea:
		// 1. Traverse the select set. For keys, they are divided into left and - > right; For values, the single character ch after traversal:
				// Pair left and ch as the key of TABLE, and - > right as the value
	// The form of map key value pairs has more space and high query efficiency
	char left_ch;
	string right;
	set<char> chars;
	for (auto iter = SELECT.begin(); iter != SELECT.end(); ++iter) // Traverse the select collection
	{
		left_ch = iter->first[0]; // Get left
		right = iter->first.substr(1); // Get - > right
		chars = iter->second;
		// Traverse chars. Put them one by one
		for (char ch : chars) { // Traversal Terminator
			TABLE.insert(pair<pair<char, char>,string>(pair<char, char>(left_ch, ch),right));
		}
	}
	/*cout << "Analysis table debugging: "< table. Find (pair < char, char > ('e ',' I ')) - > second;*/
	// Output analysis table
	printTable();
}
// Output forecast analysis table
void printTable() {
	// Output analysis table
	cout << setw(75) << right << setfill('=') << "Forecast analysis table====================" << endl;
	cout << setw(9) << left << setfill(' ') << "VN/VT";
	set<string> vts = Vt;
	vts.erase("~");
	vts.insert("#");
	for (string str : vts) // Traversal Terminator
	{
		cout << setw(12) << left << setfill(' ') << str;
	}
	cout << endl << endl;
	for (string vn : Vn)
	{
		cout << setw(7) << left << setfill(' ') << vn;
		for (string vt : vts) // Traversal Terminator
		{
			if (TABLE.find(pair<char, char>(vn[0], vt[0])) == TABLE.end()) //If not found
			{
				cout << setw(12) << left << "ERR" << " ";
			}
			else {
				cout << setw(12) << left << TABLE.find(pair<char, char>(vn[0], vt[0]))->second << " ";
			}
		}
		cout << endl;
	}

	cout << setw(75) << setfill('=') << " " << endl;
}

// Parse string
void LL1Analyse() {
	// Solution idea:
		//1. Build first in and then out of the stack, and put #, S into the stack
		//2. Traverse the sentences, send a symbol by symbol; and send X at the top of the stack to enter the analysis
			// 2.1 if X is a terminator
				// If it is equal to a, the match is successful: X comes out of the stack and reads the next character
				// Otherwise, it cannot be matched: fail to exit
			// 2.2 if X is the end character
				// a is also the end character and accepts the analysis string: exit successfully
				// a is not the end character. It does not accept the analysis string. Exit after failure
			// 2.3 otherwise, X is a non terminator
				// Look up the prediction analysis table to see if there is an expression
					// If not, the analysis will fail and exit
					// If yes, the X element goes out of the stack and the expression goes into the stack in reverse order. Continue to cycle the sentence and analyze a repeatedly
		//3. The traversal is completed and the program ends
	cout << "Construction is complete, please enter the string you want to analyze..." << endl;
	string str; // Input string
	cin >> str; 
	str.push_back('#'); //  End with Terminator
	cout << "Analyzing..." << endl;
	cout << endl << setw(75) << right << setfill('=') << "Analysis process====================" << endl;

	cout << setw(16) << left << setfill(' ') << "step";
	cout << setw(16) << left << setfill(' ') << "Analysis stack";
	cout << setw(16) << left << setfill(' ') << "Remaining input string";
	cout << setw(16) << left << setfill(' ') << "Analysis of the situation" << endl;

	stack<char> stack_a; // Analysis stack
	stack_a.push('#'); //  End character stack
	stack_a.push(S[0]); // Start symbol stack

	// Initialize display data
	int step = 1; // Number of steps
	stack<char> stack_remain = stack_a; // Residual analysis stack
	string str_remain = str; // Residual analysis string
	string str_situation = "To be analyzed"; // Analysis of the situation

	// Initial data display
	cout << setw(16) << left << setfill(' ') << step;
	cout << setw(16) << left << setfill(' ') << getStackRemain(stack_remain);
	cout << setw(16) << left << setfill(' ') << str_remain << endl;

	// Traverse the input sentences and analyze them character by character
	for (auto iter = str.begin(); iter != str.end();) {
		char a = *iter; // The current terminator is sent to a
		char X = stack_a.top(); // Stack top element sent to X

		if (isVt(X)) // If X is the Vt terminator, the top element is out of the stack and the next character is read
		{
			if (X == a) // Match input character
			{
				stack_a.pop(); // Remove stack top element
				// Remove this element from the remaining analysis string
				for (auto i_r = str_remain.begin(); i_r != str_remain.end(); i_r++)
				{
					if (*i_r == a) {
						str_remain.erase(i_r);
						break; // Delete only the first one,
					}
				}
				// Reassemble Prompt string
				string msg = """ + string(1, a) + ""matching";
				str_situation = msg;
				// Read next character
				++iter; 
			}
			else { // Unable to match, analysis error
				cout << "Analysis error:" <<X<<"and" <<a<< "Mismatch" << endl;
				exit(-1); // Error exit
			}
		}
		else if (X == '#'/ / end of grammar analysis
		{
			if (a == '#'/ / the current symbol is also the last symbol. Accept the analysis result
			{
				cout << "At the end of parsing, the current grammar accepts the string you entered" << endl;
				exit(0); // Exit successfully
			}
			else {
				cout << "Parsing error, grammar input string not ended" << endl;
				exit(-1);
			}
		}
		else { // X is a non terminator
			// Check whether TABLE (X, a) has results
			if (TABLE.find(pair<char, char>(X, a)) == TABLE.end()) //If not found
			{
				if (!canToEmpty(X)) // You can't push it empty
				{
					cout << "Analysis error,Expression not found" << endl;
					exit(-1); // Failed exit
				}
				else {  // Can be pushed empty,
					stack_a.pop(); // Remove stack top element 	//  Reassemble string
					str_situation.clear();
					str_situation.push_back(X);
					str_situation = str_situation + "->";
					str_situation = str_situation + "~";
				}
			} 
			else {
				stack_a.pop();// Stack the current symbol first
				string str = TABLE.find(pair<char, char>(X, a))->second.substr(2); // Get the expression and put it on the stack in reverse order (remove - >)
				// Reassemble string
				str_situation.clear();
				str_situation.push_back(X);
				str_situation = str_situation + "->";
				str_situation = str_situation +str;

				reverse(str.begin(),str.end());
				for (auto iiter = str.begin(); iiter != str.end(); ++iiter)
				{
					if (*iiter != '~')
					{
						stack_a.push(*iiter);
					}
				}
				// (to continue recognizing this character)
			}
		}
		// Reset display data
		++step; // Number of steps plus 1
		stack_remain = stack_a; // Set the remaining stack as the current stack
		// Display once per cycle
		cout << setw(16) << left << setfill(' ') << step;
		cout << setw(16) << left << setfill(' ') << getStackRemain(stack_remain);
		cout << setw(16) << left << setfill(' ') << str_remain;
		cout << setw(16) << left << setfill(' ') << str_situation << endl;
	}
}


// =====================================Tool function===================================
// Returns the right set of a production based on the left
vector<string> getRights(string left)
{
	vector<string> rights;
	if (grammar.find(left)== grammar.end()) // If there is no such item in the syntax, it will directly return null
	{
		return rights;
	}
	else {
		string str = grammar.find(left)->second;

		str = str + '|';   // Add a separator at the end to intercept the last piece of data
		size_t pos = str.find('|');//The return value of the find function. If the separator is found, the position where the separator first appears is returned,
									 //Otherwise, return npos
									 //Use size here_ The T type is to return the location
		while (pos != string::npos)
		{
			string x = str.substr(0, pos);//substr function to obtain the substring
			rights.push_back(x);          // Store in right container
			str = str.substr(pos + 1);     // Update string
			pos = str.find('|');         // Update separator position
		}
		return rights;
	}
}

// Determine whether it is a terminator or non terminator
bool isVn(char v) {
	if (v >= 'A' && v <= 'Z') { // Capital letters are non terminators
		return true;
	}
	else {
		return false;
	}
}

bool isVt(char v) {
	if (isVn(v) || v == '#'| v = =' | '/ / if it is a non terminator, end symbol or separator, it is not a terminator
	{
		return false;
	}
	return true;
}

// Judge whether a non terminator can push null
bool canToEmpty(char vn) {
	vector<string> rights = getRights(string(1,vn)); // The right set of vn
	for (auto i = rights.begin();i!=rights.end();++i) // Traverse the right set (if the front right can be pushed empty, you can jump out in advance, otherwise you will see the last)
	{
		string right = *i; // This is a right part
		// Traverse the right part
		for (auto ch = right.begin(); ch != right.end(); ++ch) {
			if ((*ch)=='~')// If ch is empty, it means that it can be pushed empty (because there is no possibility that the right part is empty)“ ε b "in this case, it does not need to see whether it is the last character)
			{
				return true;
			}
			else if (isVn(*ch)) { // If vn, recursion is required
				if (canToEmpty(*ch))// If you can push empty
				{
					// If it is the last character, return true
									//There may be "ad" a - > ε D cannot be pushed empty, so you need to see whether it is the last character
					if ((ch + 1) == right.end())
					{
						return true;
					}
					continue; // The current character can be pushed empty, but it is not the last character. It is not sure whether it can be pushed empty. You need to see the next character on the right
				}
				else  // If you can't push empty, it means that the current right part can't be pushed empty. You need to look at the next right part
					break;
			}
			else // If it is not empty vt, it means that the right part cannot be empty at present. You need to look at the next right part
				break;
		}
	}
	return false;
}

// Judge whether the intersection of two character set s is empty
bool isIntersect(set<char> as, set<char> bs) {
	for (char a : as) {
		for (char b : bs) {
			if (a == b)
			{
				return true;
			}
		}
	}
	return false;
}

// Get the string in reverse order
string getStackRemain(stack<char> stack_remain) {
	string str;// Residual analysis stack string
	while (!stack_remain.empty())
	{
		str.push_back(stack_remain.top());
		stack_remain.pop();// Out of stack
	}
	reverse(str.begin(),str.end());
	return str;
}

// Displays and outputs a char set
void printSet(set<char> sets) {
	cout << "{ ";
	for (auto i = sets.begin(); i != sets.end();) {
		cout << *i;
		if (++i != sets.end())
		{
			cout << " ,";
		}
	}
	cout << " }" << endl;
}

// Find the number of elements in the FOLLOW set
int getFS() {
	int count = 0;
	for (auto iter = FOLLOW.begin(); iter != FOLLOW.end(); ++iter) {
		count = count + iter->second.size();
	}
	return count;
}