💜 Write in front 💜

preface
We must have learned about functions in C language. I believe you have a deep understanding of functions, because functions are used in C a lot. Especially when doing projects, they are written in modules. Java also provides you with "functions", but the names are different. In Java, they are called [Methods]. Next, please look down

🌟 Basic usage of method

🌙 What is a method

A method is a code fragment. It is similar to the "function" in C language

Significance of the method:
1. It is a modular organization code (when the code scale is complex)
2. Make sure that the code is reused, and one code can be used in multiple locations
3. Make the code easier to understand
4. Directly call the existing methods for development, and there is no need to make wheels repeatedly

🌙 Method definition syntax

Basic grammar

// Method definition
public static Method return value method name([Parameter type parameter ...]){
Method body code;
[return Return value];
}
// Method call
 Return value variable = Method name(Argument...);

Code example: implement a method to add two integers

class Test {
public static void main(String[] args) {
    int a = 3;
    int b = 2;
    // Method call
    int ret = add(a, b);
System.out.println("ret = " + ret);
}
-----------------------------------------------
   // Definition of method
public static int add(int x, int y) {
     return x + y;
}
}
-----------------------------------------------
// results of enforcement
ret = 5

matters needing attention
1. The public and static keywords have specific meanings here and will not be discussed for the time being. They will be described in detail later
2. When defining a method, there can be no parameters. Each parameter must specify a type
3. During method definition, the return value can also be null. If there is no return value, the return value type should be written as void (similar to C language)
4. Parameters during method definition are called "formal parameters", and parameters during method call are called "arguments"
5. The method definition must be in the class, and the code can be written above or below the calling position
6. There is no concept of "function declaration" in Java (I think it's very cool. I'm often disgusted by the problem of function declaration in C)

🌙 Execution procedure of method call

Basic rules

• When defining a method, the code of the method will not be executed. It will only be executed when calling
• When the method is called, the argument is assigned to the formal parameter
• After the parameter is passed, it will be executed to the method body code
• When the method is executed (encounter the return statement), it is executed. Return to the method call position and continue to execute
• A method can be called multiple times

Code example 1 calculates the addition of two integers

class Test {
public static void main(String[] args) {
int a = 10;
int b = 20;
System.out.println("Before the method is called for the first time");
int ret = add(a, b);
System.out.println("After the first method call");
System.out.println("ret = " + ret);
System.out.println("Before the second method call");
ret = add(30, 50);
System.out.println("After the second method call");
System.out.println("ret = " + ret);
}
public static int add(int x, int y) {
System.out.println("In calling method x = " + x + " y = " + y);
return x + y;
}
}
// results of enforcement
 Before a method call
 In calling method x = 10 y = 20
 After the first method call
ret = 30
 Before the second method call
 In calling method x = 30 y = 50
 After the second method call
ret = 80

Code example 2: calculate 1! + 2! + 3! + 4! + 5`

class Test {
public static void main(String[] args) {
int sum = 0;
for (int i = 1; i <= 5; i++) {
sum += factor(i);
}
System.out.println("sum = " + sum);
}
public static int factor(int n) {
System.out.println("calculation n Factorial of! n = " + n);
int result = 1;
for (int i = 1; i <= n; i++) {
result *= i;
}
return result;
}
}
// results of enforcement
 calculation n Factorial of! n = 1
 calculation n Factorial of! n = 2
 calculation n Factorial of! n = 3
 calculation n Factorial of! n = 4
 calculation n Factorial of! n = 5
sum = 153

Use method, avoid using double loop, and make the code simpler and clearer

🌙 Relationship between arguments and formal parameters (key points)

Code example: exchanging two integer variables

class Test {
public static void main(String[] args) {
int a = 10;
int b = 20;
swap(a, b);
System.out.println("a = " + a + " b = " + b);
}
public static void swap(int x, int y) {
int tmp = x;
x = y;
y = tmp;
}
}
// Operation results
a = 10 b = 20

Cause analysis
The code just now did not complete the data exchange
For the basic type, the formal parameter is equivalent to a copy of the argument, that is, a value passing call

int a = 10;
int b = 20;
int x = a;
int y = b;
int tmp = x; x = y; y = tmp;

As you can see, the modifications to x and y do not affect a and b
Solution: because in Java, you can't get the address on the stack!
So we solve this problem by passing reference type parameters (such as arrays)

class Test {
public static void main(String[] args) {
int[] arr = {10, 20};
swap(arr);
System.out.println("a = " + arr[0] + " b = " + arr[1]);
}
public static void swap(int[] arr) {
int tmp = arr[0];
arr[0] = arr[1];
arr[1] = tmp;
}
}
// Operation results
a = 20 b = 10

🌙 Method with no return value

The return value of the method is optional. It may not be available sometimes

Code example

class Test {
public static void main(String[] args) {
int a = 10;
int b = 20;
print(a, b);
}
public static void print(int x, int y) {
System.out.println("x = " + x + " y = " + y);
}
}

In addition, the method of exchanging two integers just now has no return value

🌟 Method overload

Sometimes we need to use a function compatible with multiple parameters at the same time, we can use method overloading

🌙 Overload problem to be solved·

Code example

public static void main(String[] args) {
int a = 10;
int b = 20;
int ret = add(a, b);
System.out.println("ret = " + ret);
double a2 = 10.5;
double b2 = 20.5;
double ret2 = add(a2, b2);
System.out.println("ret2 = " + ret2);
}
public static int add(int x, int y) {
return x + y;
}
}
// Compilation error
Test.java:13: error: Incompatible types: from double Convert to int There may be losses
               double ret2 = add(a2, b2);

The existing add method cannot be used directly because the parameter types do not match

Modified code

class Test {
public static void main(String[] args) {
int a = 10;
int b = 20;
int ret = addInt(a, b);
System.out.println("ret = " + ret);
double a2 = 10.5;
double b2 = 20.5;
double ret2 = addDouble(a2, b2);
System.out.println("ret2 = " + ret2);
}
public static int addInt(int x, int y) {
return x + y;
}
public static double addDouble(double x, double y) {
return x + y;
}
}

This way of writing is right (for example, Go language does this)
However, Java thinks that the name addInt is unfriendly, so it's better to call it add directly

🌙 Use overload

Code example

class Test {
public static void main(String[] args) {
int a = 10;
int b = 20;
int ret = add(a, b);
System.out.println("ret = " + ret);
double a2 = 10.5;
double b2 = 20.5;
double ret2 = add(a2, b2);
System.out.println("ret2 = " + ret2);
double a3 = 10.5;
double b3 = 10.5;
double c3 = 20.5;
double ret3 = add(a3, b3, c3);
System.out.println("ret3 = " + ret3);
}
public static int add(int x, int y) {
return x + y;
}
public static double add(double x, double y) {
return x + y;
}
public static double add(double x, double y, double z) {
return x + y + z;
}
}

Methods are all called add. However, some add calculates the addition of int, some double, some two numbers, and some three numbers
The same method name, which provides different versions of implementations, is called method overloading

🌙 Overloaded rules

For the same class or inheritance relationship:

• Same method name
• Method has different parameters (number of parameters or parameter type)
• The return value type of the method does not affect overloading

Code example

public static int add(int x, int y) {
return x + y;
}
public static double add(double x, double y) {
return x + y;
}
public static double add(double x, double y, double z) {
return x + y + z;
}
}
class Test {
public static void main(String[] args) {
int a = 10;
int b = 20;
int ret = add(a, b);
System.out.println("ret = " + ret);
}
public static int add(int x, int y) {
return x + y;
}
public static double add(int x, int y) {
return x + y;
}
}
// Compilation error
Test.java:13: error: Already in class Test Methods are defined in add(int,int)
       public static double add(int x, int y) {
                            ^ 1 Errors

When two methods have the same name and parameters,
However, when the return value is different, it does not constitute an overload

🌟 Method recursion

If an object part contains itself or defines itself by itself, then we say that the object is recursive; if a process calls itself directly or indirectly, then the process is recursive. The idea of recursion is to decompose the problem into smaller subproblems with the same solution as the original problem, so it can make our way of thinking simpler and our program easier More concise. However, in terms of recursive functions, recursion increases stack pressing overhead, so [space complexity is relatively high].

🌙 The concept of recursion

Recursion is equivalent to mathematical induction. It has a starting condition and then a recursive formula
Recursion condition:
(1) Reduce the scale of the problem and make the subproblem have the same solution as the original problem.
(2) Set the exit. If there is no exit, the program will recurse all the time.

For example, we ask N!
Starting condition: when N = 1, N! Is 1. This starting condition is equivalent to the end condition of recursion
Recursive formula: find N!, it is not easy to find directly. You can convert the problem into N! = > N * (N-1)!

Code example: recursively find the factorial of N

public static void main(String[] args) {
   int n = 5;
   int ret = factor(n);
   System.out.println("ret = " + ret);
}
public static int factor(int n) {
   if (n == 1) {
       return 1;
  }
   return n * factor(n - 1); This code is the key factor Function call function itself
}
// results of enforcement
ret = 120

The key to this code is [factor function calling function itself]. Next, please see the detailed analysis

🌙 Recursive execution process analysis

The execution process of recursive programs is not easy to understand. To understand recursion clearly, you must first understand the "method execution process", especially "after the method execution is completed, return to the calling position and continue to execute"

Code example: recursively find the factorial of N, step print

public static void main(String[] args) {
   int n = 5;
   int ret = factor(n);
   System.out.println("ret = " + ret);
}
public static int factor(int n) {
   System.out.println("Function start, n = " + n);
   if (n == 1) {
       System.out.println("End of function, n = 1 ret = 1");
       return 1;
  }
   int ret = n * factor(n - 1);
   System.out.println("End of function, n = " + n + " ret = " + ret);
   return ret; }

-------// Set the factorial of 5, and the execution result is as follows------------------------
        
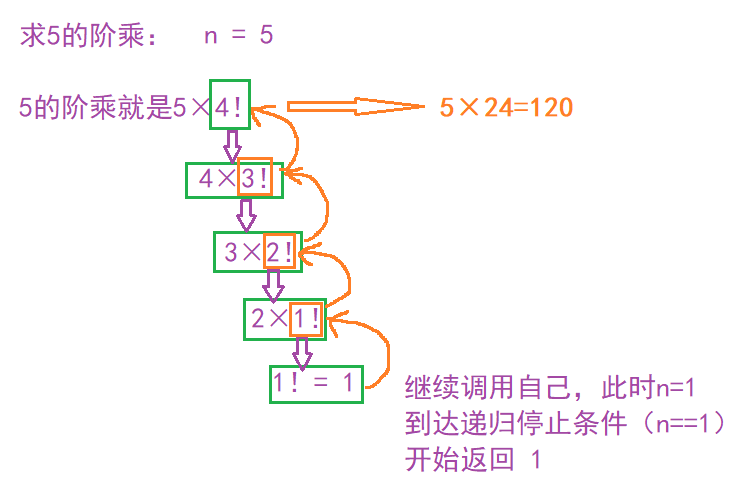
             Function start, n = 5  //Call yourself
             Function start, n = 4  //Call yourself
             Function start, n = 3  //Call yourself
             Function start, n = 2  //Call yourself
             Function start, n = 1  //When the stop condition is reached, return 1

-------//When the termination condition is reached, the return value is returned one layer at a time---------------------
   
             End of function, n = 1 ret = 1
             End of function, n = 2 ret = 2
             End of function, n = 3 ret = 6
             End of function, n = 4 ret = 24
             End of function, n = 5 ret = 120
             ret = 120

Execution process diagram

🌙 Recursive exercise

Code example 1
Print each bit of a number in sequence (for example, 1234 prints 1 2 3 4)

public static void print(int num) {
   if (num > 9) {
       print(num / 10);
  }
   System.out.println(num % 10);
}

Code example 2
Recursively find 1 + 2 + 3 +... + 10

public static int sum(int num) { 
if (num == 1) { 
return 1; 
} 
return num + sum(num - 1); 
}

Code example 3
Write a recursive method, enter a nonnegative integer and return the sum of the numbers that make up it. For example, if you enter 1729, you should return 1 + 7 + 2 + 9, and its sum is 19

public static int sum(int num) { 
if (num < 10) { 
return num; 
} 
return num % 10 + sum(num / 10); 
}

Code example 4 (key!! key!! key!!)
Find the nth item of Fibonacci sequence [Fibonacci sequence is a group of first and second digits of 1, starting from the third, and the latter is a group of incremental sequence of the first two digits, such as 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55...]

Method 1: cycle
This solution is a more efficient solution
Time complexity O(n), space complexity O(1)

import java.util.Scanner;
public class Fibonacci number {//Time complexity O(n), space complexity O(1)
   public static void main(String[] args) {
       Scanner scn = new Scanner(System.in);
       int n = scn.nextInt();
       int a = 0;
       int b = 1;
       int tmp = 0;
       if (n==1){
           System.out.println(0);
       }
       else if (n==2){
           System.out.println(1);
       }
       else if (n>2) {
           for ( int i = 3; i <= n; i++ ) {
               tmp = a+b;
               a = b;
               b = tmp;
           }
           System.out.println(b);
       }
   }
}

Method 2: recursion
The way of thinking of this solution is very simple
However, the time complexity is particularly high, including time complexity O(2^n) and space complexity O(n)
This method is not recommended.

import java.util.Scanner;
public class Recursive Fibonacci sequence {//Time complexity O(2^N), space complexity O(n)
    public static int count = 0;
    public static int Fib(int n) {
        if (n==1)
           return 0;
        else if (n==2||n==3)
          return 1;
       else if (n==4)
          count++;
        return Fib(n-1)+Fib(n-2);
    }
   public static void main(String[] args) {
       Scanner scn = new Scanner(System.in);
       while (scn.hasNextInt()) {
           int n = scn.nextInt();
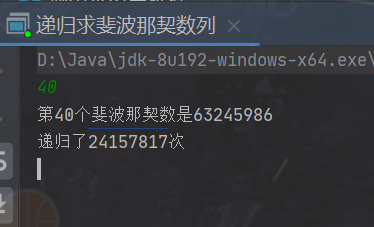
           System.out.println("The first"+n+"The Fibonacci number is"+Fib(n));
           System.out.println("Recursion"+count+"second");
           count = 0;
       }
   }
}

It can be seen that when finding the 40th Fibonacci number, the number of repetitions is as high as 24157817

Method 3: efficient recursion
If the former recursive solution is calculated from back to front, then this solution is calculated from front to back,
This recursive method belongs to tail recursion. Therefore, during recursion, the function will only use the stack space opened by pressing the stack for the first time to cycle in one stack space without opening up other stack spaces
Therefore, this method with time complexity of O(n) and space complexity of O(1) is a very efficient recursive method.

import java.util.Scanner;
public class Efficient recursive calculation of Fibonacci sequence { //Time complexity O(n), space complexity O(1)
   public static int Fib(int first,int sec,int n) {
       if (n==1)
           return first;
       else
           return Fib(sec,first+sec,n-1);
   }
  public static void main(String[] args) {
       Scanner scn = new Scanner(System.in);
       while (scn.hasNextInt()) {
           int n = scn.nextInt();
           System.out.println("The first"+n+"The Fibonacci number is"+Fib(0,1,n));
       }
   }
}

🌙 Recursive summary

Recursion is an important way to solve programming problems
Some problems are naturally defined recursively (such as Fibonacci sequence, binary tree, etc.), so it is easy to use recursive solutions
Some problems can be solved by using recursion and non recursion (loop). It is more recommended to use loop at this time. Compared with recursion, non recursive programs are more efficient

        ❤ Originality is not easy. If there is any error, please leave a message in the comment area. Thank you very much ❤
        ❤                 If you think the content is good, it's not too much to give a three company~        ❤
        ❤                              I'll pay a return visit when I see it~                                       ❤