Representation and processing of information
The three most important numbers represent:
Unsigned( unsigned)Coding is based on the traditional binary representation, which represents numbers greater than or equal to zero. Complement( two' s-complement)Coding is the most common way to represent signed integers. Signed integers are numbers that can be positive or negative. Floating point number( floating-point)Coding is a radix-2 version of the scientific notation that represents real numbers.
Computer representation uses a limited number of bits to encode a number. Therefore, when the result is too large to represent, some operations will overflow.
Information storage
Most computers use 8-bit blocks, or byte s, as the smallest addressable unit of memory, rather than accessing individual bits in memory.
Machine level programs regard memory as a very large byte array, which is called virtual memory.
Each byte of memory is identified by a unique number, called its address, and the set of all possible addresses is called virtual address space.
The function of pointer in C language
Pointer is C An important feature of language. It provides a mechanism for referencing elements of data structures, including arrays. Two aspects of pointers: value and type. Its value represents the location of an object, and its type represents the type of object stored in that location (such as integer or floating-point number).
Hexadecimal notation
A byte consists of 8 bits.
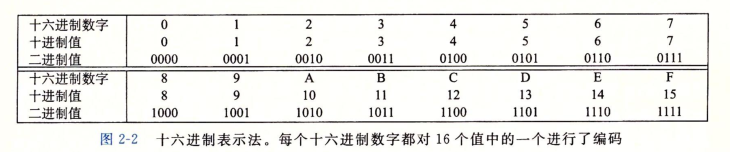
In C language, numeric constants starting with 0x or 0x are considered hexadecimal values.
The characters' A '~' F 'can be uppercase or lowercase.

Word data size
Each computer has a word size indicating the nominal size of the pointer data.
The most important system parameter determined by word length is the maximum size of virtual address space.
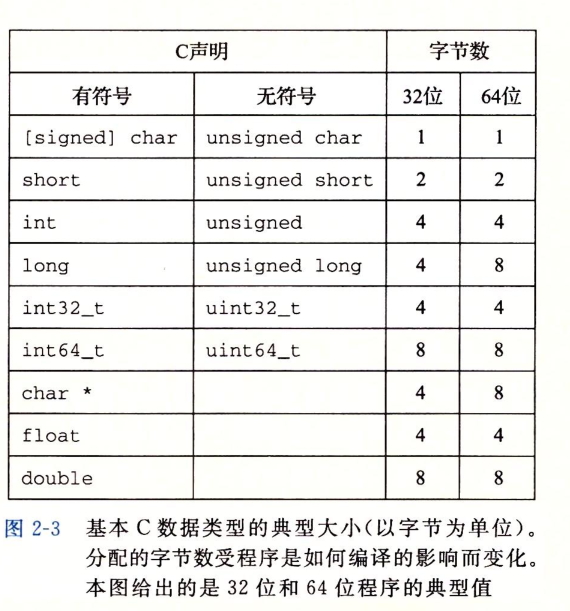
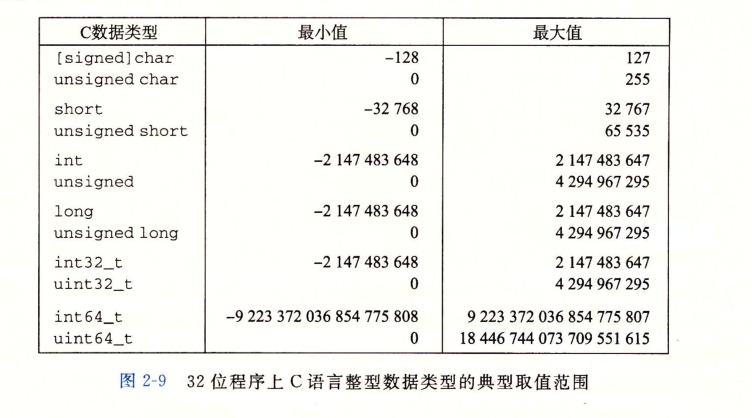
Integers or are signed, that is, they can represent negative numbers, zero and positive numbers; Or it is unsigned, that is, it can only represent non negative numbers. C Data type for char Represents a single byte.
Most machines support two different floating point formats:
Single precision (in C Declared as float)And double precision (in C Declared as double). The two formats distinguish between 4 bytes and 8 bytes.

Addressing and byte order
For program objects that span multiple bytes, we must establish two rules:
What is the address of this object and how to arrange these bytes in memory.
There are two general rules for arranging bytes representing an object:
Big endian method: the most significant byte is in front
Small end method: the most significant byte follows
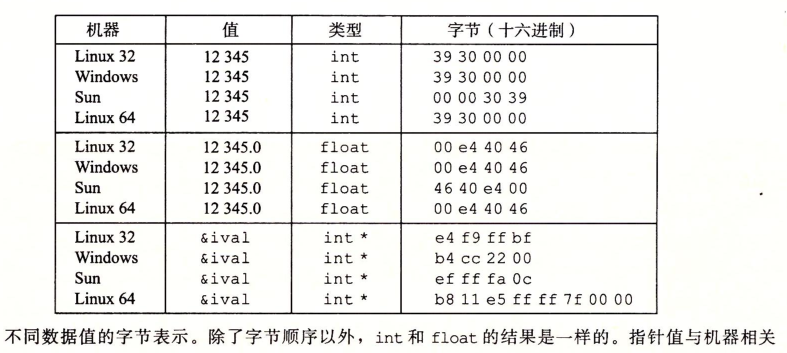
Example:
Hypothetical variable x The type of is int ,At address 0 x100 At, its sample hexadecimal value is 0 x01234567. Address range 0 x100~0x103 The byte order of depends on the type of machine:


Represents a string
C In a language, a string is encoded as a null (An array of characters whose value is at the end of the (0) character Each character is represented by a standard encoding, the most common being ASCII Character code.
Representation code

Instruction codes are different.
Different machine types use different and incompatible instructions and coding methods. Even the same process running on different operating systems will have different coding rules, so binary codes are incompatible.
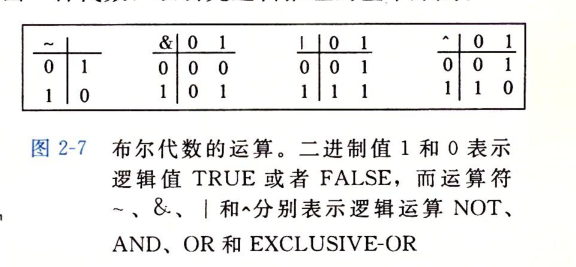
Boolean algebra
Boolean Algebra: by encoding the logical values TRUE and FALSE into binary 1 and 0, an algebra can be designed to study the basic principles of logical reasoning.
The simplest Boolean algebra is defined on the basis of binary set {0,1}.
Bit level operation in C language
A useful feature of C language is that it supports bitwise Boolean operations.
| namely OR(Or) & namely AND(And) ~ namely NOT((reverse) ^ namely EXCLUSIVE-OR(Exclusive or)
An example of evaluating a char data type expression:

A common use of bit level operation is to implement mask operation. Here mask is a bit pattern that represents the set of bits selected from a word.
Logical operation in C language
C language also provides a set of logical operators:
|| OR && AND ! NOT Logical operations assume that all non-zero parameters represent TRUE,The parameter 0 indicates FALSE. Return 1 or 0, respectively, indicating that the result is TRUE perhaps FALSE.
Example:
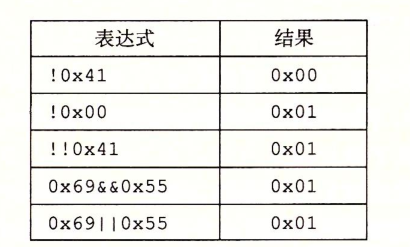
Logical operator&&and|| Bit level operations corresponding to them & and | The second important difference between is: If evaluating the first parameter determines the result of the expression, the logical operator will not evaluate the second parameter.
Shift operation in C language
C language also provides a set of shift operations, moving bit patterns to the left or right.



Integer representation
Describes two different ways to encode integers in bits:
One can only represent non negative numbers, while the other can represent non negative, zero and positive numbers.

Integer Data Type
C language supports multiple integer data types -- representing a limited range of integers.
Each type can use keywords to specify the size, including char, short and long. At the same time, it can also indicate that the represented number is non negative (declared as unsigned) or may be negative (default).


Encoding of unsigned numbers


Complement coding



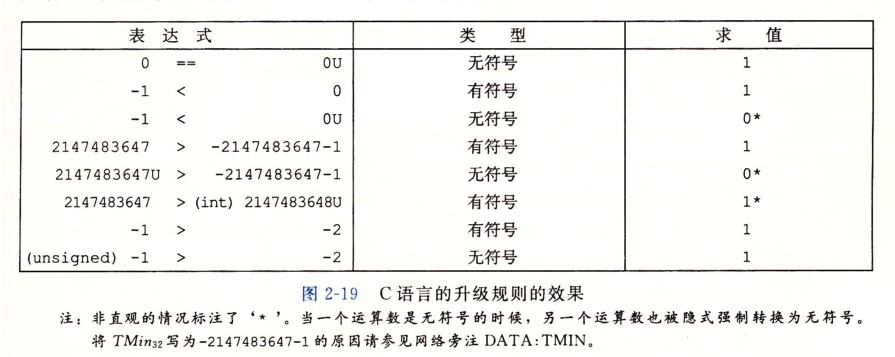
Conversion between signed and unsigned numbers
C language allows forced type conversion between various digital data types.
For example, suppose the variable x is declared as int and u is declared as unsigned. The expression (unsigned) x converts the value of X to an unsigned value, and (int) u converts the value of u to a signed integer.


Signed and unsigned numbers in C language
C language supports signed and unsigned operations of all integer data types.
Although the C language standard does not specify a representation of signed numbers, almost all machines use complement. Usually, most numbers are signed by default.
For example, when a constant such as 12345 or Ox1A2B is declared, the value is considered signed. To create an unsigned constant, you must add the suffix character 'u' or 'u', for example, 123450 or Ox1A2Bu.
Extends the bit representation of a number
A common operation is to convert integers of different word lengths while keeping the value unchanged. Of course, this is impossible when the target data type is too small to represent the desired value. However, it should always be possible to convert from a smaller data type to a larger type.
To convert an unsigned number to a larger data type, we simply add 0 at the beginning of the representation. This operation is called zero extension, and the representation principle is as follows:
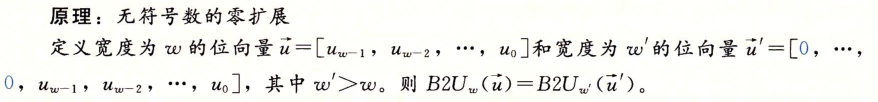
To convert a complement number to a larger data type, you can perform a sign exten sion - sion), add the value of the most significant bit to the representation, which is expressed as the following principle. We highlight its role in symbol expansion by marking the symbol bit in blue.

Truncated number


Integer operation
The addition of two positive numbers results in a negative number, and the comparison expression x<y And comparison expressions x- y<O Will produce different results. These attributes are caused by the limitation of computer operation.
Unsigned addition

Arithmetic operation overflow means that the complete integer result cannot be put into the word length limit of the data type.


Complement addition


Complement non

Unsigned multiplication

Complement multiplication

Multiply by constant


Multiply the unsigned number by the power of 2, It is equivalent to shifting the unsigned number to the left k Bit to interpret the result as unsigned. Multiply the signed number represented by the complement by the power of 2, It is equivalent to shifting the signed number to the left k Bit to interpret the result as a complement.
Divided by the power of 2

Floating point number
IEEE Floating point number
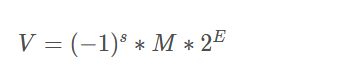
For 32-bit floating-point numbers, s Occupy the highest position E Occupy the next highest 8 places M Occupy the lower 23 places For 64 bit floating point numbers, s Occupy the highest position E Occupy the second highest 11 places M Occupy the lower 52 places Explanation: Set E Part length is k,M Part length is t 1.1. When E When all are binary 0,
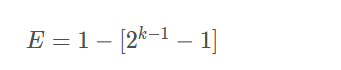
M=0.t individual M Partial binary sequence 1.2. When E When all are binary 1, When M When some parts are not all 0, it means NaN When M When all parts are 0, it indicates positive infinity or negative infinity [depending on the symbol] 1.3. When E When not all are 0 or 1,
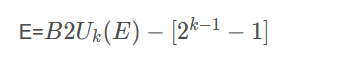
M=1.t individual M Partial binary sequence from int Turn into float,Numbers do not overflow, but may be rounded. from int or float Turn into double,Exact values can be retained from double change into float,Possible overflow is positive infinity and negative infinity. May be rounded. from float or double Turn into int,May overflow. The value is rounded to 0.
Learning References:
<In depth understanding of computer systems, 3rd Edition https://blog.csdn.net/x13262608581/article/details/107291692