catalogue

preface

Linked list

Concept and structure of linked list

Classification of linked lists

1. One way or two-way

2. Lead or not lead  

3. Cyclic or non cyclic

Implementation of single linked list

Print linked list

Application node

Tail insertion

Head insert

Tail deletion

Header deletion

Insert after specified position  

Delete at specified location  

lookup

Destroy linked list

Complete code

Force buckle linked list OJ

Difference between sequential list and linked list

preface

In the last chapter, we learned the sequence table and realized the addition, deletion, query and modification of the sequence table.

Of course, some advantages and disadvantages of the sequence table are also found. Let's review:

advantage:

1. Support random access, which can be accessed directly through subscript.
2. You can sort.

Disadvantages:

1. Insertion and deletion of middle / head, with time complexity of O(N)
2. To increase capacity, you need to apply for new space, copy data and release old space. There will be a lot of consumption.
3. The capacity increase is generally double, which is bound to waste some space.

So in order to make up for these shortcomings, there is a linked list, so what is a linked list?

Linked list

Concept and structure of linked list

Concept: linked list is a non continuous and non sequential storage structure in physical storage structure. The logical order of data elements is realized through the pointer link order in the linked list.
It is still abstract only according to the text description. Observe directly from the above figure:

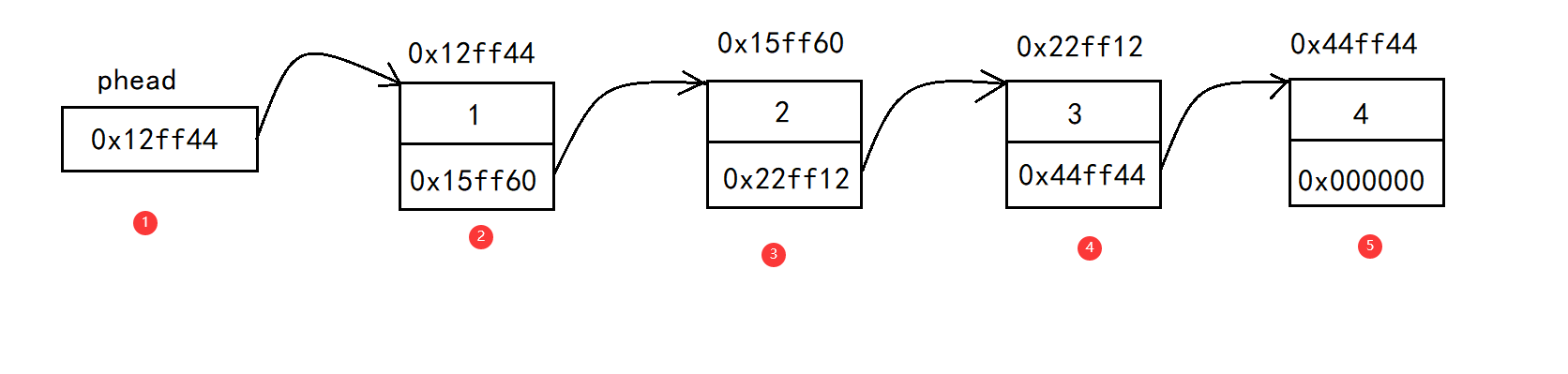
In the figure: 2.3.4.5 are all structures, called nodes. Different from the sequence table, each node in the linked list does not simply store one data. It is a structure whose members include a stored data and the address of the next node. In addition, the addresses in the sequential list are continuous, while the addresses of nodes in the linked list are randomly assigned.

How does the linked list work?

The address of the first node is stored in the phead pointer in the figure, so we can find the structure according to the pointing address. Because the address of the next structure is stored in the structure, we can find the second structure. We can find all nodes in a cycle until the structure with empty address is stored.

Note: the arrows in the figure do not actually exist. They are only here for convenience of understanding.

be careful:

1. As can be seen from the figure, the chain structure is logically continuous, but not necessarily continuous physically.
2. In reality, nodes are generally applied from the heap.
3. The space applied from the heap is allocated according to certain strategies. The space applied for two times may or may not be continuous.

Classification of linked lists

In practice, the structure of linked list is very diverse. There are eight linked list structures when the following situations are combined:

1. One way or two-way

2. Lead or not lead  

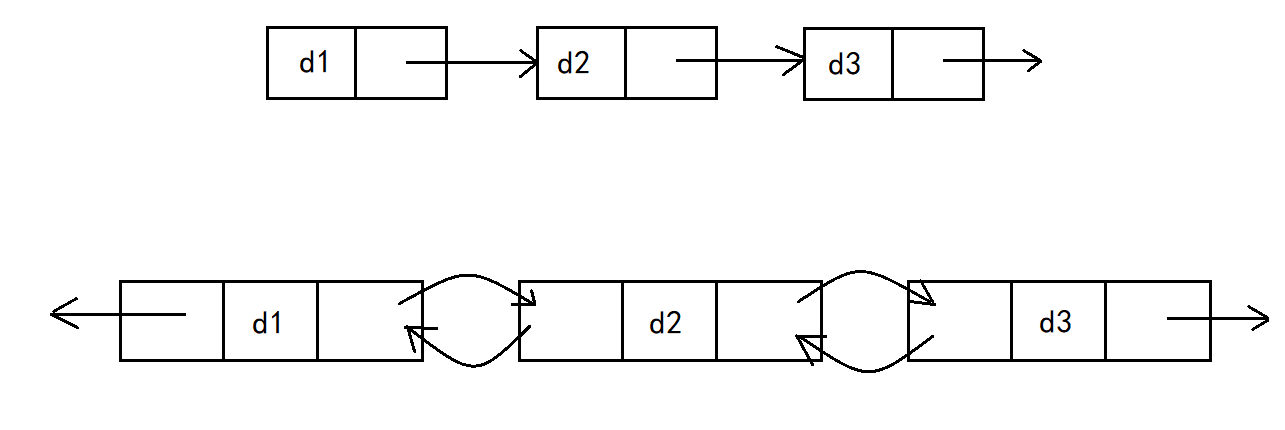
3. Cyclic or non cyclic

Although there are so many linked list structures, two structures are most commonly used in practice:  

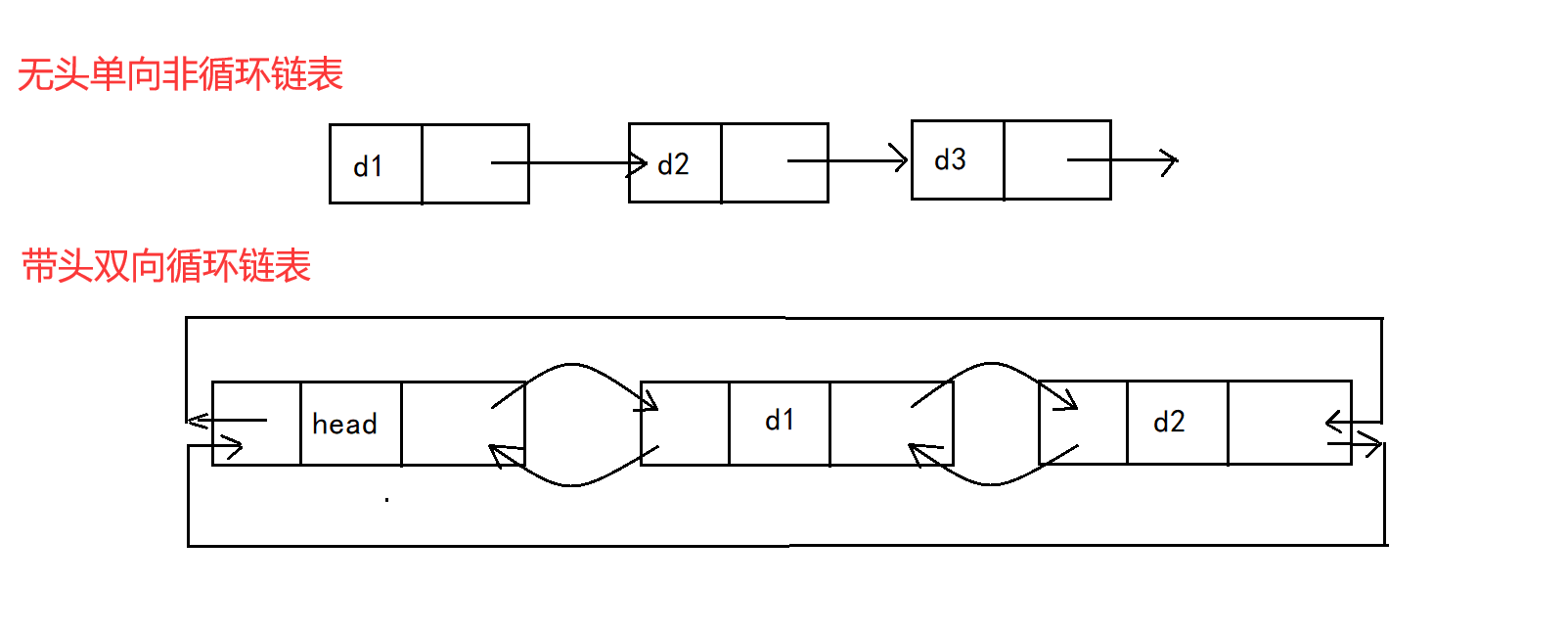1. Headless one-way acyclic linked list: it has a simple structure and is generally not used to store data alone. In fact, it is more used as a substructure of other data structures, such as hash bucket, adjacency table of graph and so on. In addition, this structure appears a lot in the written interview.
2. Lead two-way circular linked list: it has the most complex structure and is generally used to store data separately. The linked list data structure used in practice is a two-way circular linked list. In addition, although the structure is complex, you will find that the structure will bring many advantages after code implementation, but the implementation is simple. We will know after code implementation.

Implementation of single linked list

#pragma once

#include<stdio.h>
#include<assert.h>
#include<stdlib.h>

typedef int SLTDataType;

typedef struct SListNode
{
	SLTDataType data;
	struct SListNode* next;//Address of the next node

}SListNode;


//Print linked list
void SListPrint(SListNode* phead);

//Application node
SListNode* SListBuyNode(SLTDataType x);

//Because we point to the head node of the linked list through a pointer, and because the head node of the linked list may be changed during insertion and deletion, the following parameters need to pass the secondary pointer
//Tail insertion
void SListPushBack(SListNode** pphead, SLTDataType x);

//Head insert
void SListPushFront(SListNode** pphead, SLTDataType x);

//Tail deletion
void SListPopBack(SListNode** pphead);

//Header deletion
void SListPopFront(SListNode** pphead);


//lookup
SListNode* SListFind(SListNode* phead, SLTDataType x);

//Insert after specified position
void SListInsert(SListNode** pphead, SListNode* pos, SLTDataType x);

//Delete after specified location
void SListErase(SListNode** pphead, SListNode* pos);

//Destroy linked list
void SListDestory(SListNode** pphead);

Print linked list

In the sequence table, each element is accessed through subscript. The linked list is different from the sequence table. After accessing the data of this node, you need to find the next node through the address stored in this node.

//Print linked list
void SListPrint(SListNode* phead)
{
	SListNode* cur = phead;//Generally, instead of directly moving the head pointer, create a pointer variable to move it
	while (cur)//Ends the loop when the pointer is null
	{
		printf("%d->", cur->data);//Print the data of this node
		cur = cur->next;//Point the pointer to the next node
	}
	printf("NULL\n");
}

Application node

Each node of the linked list is dynamically opened (malloc), and the size of each node is the size of the structure.

After successful development, the data stored in the node shall be set to the value to be stored, and the address stored in the node shall be set to NULL.

//Application node
SListNode* SListBuyNode(SLTDataType x)
{
	SListNode* newnode = (SListNode*)malloc(sizeof(SListNode));
	if (newnode == NULL)//Judge whether the node is successfully opened
	{
		perror("malloc:");
		exit(-1);
	}
	newnode->data = x;
	newnode->next = NULL;
	return newnode;//Return node address
}

Tail insertion

Because the element cannot be accessed according to the subscript (that is, it cannot be accessed randomly), of course, we do not know the location of the last node. When tailoring, we need to traverse to find the location of the last node.

At the same time, there are two situations:

1. If the linked list is empty, you can insert it directly.
2. If the linked list is not empty, you need to find the tail node and insert it.

//Tail insertion
void SListPushBack(SListNode** pphead, SLTDataType x)
{
	assert(pphead);
    SListNode* newnode = SListBuyNode(x);//Application node
	if (*pphead == NULL)//1. The linked list is empty
	{
		*pphead = newnode;//Directly set the head node as the node to be inserted
	}
	else
	{
		SListNode* cur = *pphead;
		while (cur->next)//Tail finding node
		{
			cur = cur->next;
		}
		cur->next = newnode;//Set the address stored in the tail node as the address of the insertion node
	}
}

Head insert

Header insertion is relatively simple. Directly set the next of the application node as the header node, and then change the header node to the application node

Note: there is no need to consider whether the linked list is empty.

//Head insert
void SListPushFront(SListNode** pphead, SLTDataType x)
{
    assert(pphead);
	SListNode* newnode = SListBuyNode(x);
	newnode->next = *pphead;//Set the address saved in the application node as the address of the head node
	*pphead = newnode;//Then move the head node to the right
}

Tail deletion

Like tail insertion, we do not know the address of the tail node, so we need to find the tail node first.

At the same time, three situations need to be considered:

1. The linked list is empty.
2. There is only one node in the linked list.
3. There is more than one node in the linked list.

//Tail deletion
void SListPopBack(SListNode** pphead)
{
    //1. If the linked list is empty, the node cannot be deleted, and the pointer cannot be empty
	assert(*pphead && phead);

    //2. There is only one node in the linked list. Release the node directly, and then set the node to NULL
	if ((*pphead)->next == NULL)
	{
		free(*pphead);
		*pphead = NULL;
		return;
	}

    //3. If there is more than one node in the linked list, find the tail node first, release the tail node and set it to NULL
    //  But this is not enough, because the penultimate node still has the address of the tail node, so it needs to be set to NULL
	SListNode* cur = *pphead;//Used to mark the penultimate node
	SListNode* next = (*pphead)->next;//Tag tail node
	while (next->next)
	{
		next = next->next;
		cur = cur->next;
	}
	cur->next = NULL;//Set the address stored in the penultimate node to NULL
	free(next);//Release tail node
	next = NULL;
}

Header deletion

Header deletion is also relatively simple, which is equivalent to moving the header pointer to the second node.

There are two situations:

1. The linked list is empty.
2. The linked list is not empty.

//Header deletion
void SListPopFront(SListNode** pphead)
{
	assert(*pphead && phead);//The linked list is empty and cannot be deleted
	SListNode* next = (*pphead)->next;//Record the address of the second node
	free(*pphead);//Release header node
	*pphead = next;//Point the pointer to the second node
}

Insert after specified position  

The reason for inserting after the specified position rather than before is that when inserting in front, you need to find the address in front of the insertion position, and this will traverse the linked list again. The time complexity is O(N), while when inserting in the back, you can insert directly, and the time complexity is O(1).

//Insert after specified position
void SListInsert(SListNode** pphead, SListNode* pos, SLTDataType x)
{
	assert(pphead && pos);
	SListNode* newnode = SListBuyNode(x);//Application node
	SListNode* next = pos->next;//Find the address of the next node at the insertion location
	pos->next = newnode;//Insert Knot 
	newnode->next = next;//Connect to the following linked list

}

// Insert a node before the pos position
void SListInsert(SLTNode** pphead, ListNode* pos, SLTDateType x)
{
	assert(pphead);
	assert(pos);

	ListNode* newnode = BuyListNode(x);
	if (*pphead == pos)
	{
		newnode->next = *pphead;
		*pphead = newnode;
	}
	else
	{
		// Find the previous position of pos
		ListNode* posPrev = *pphead;
		while (posPrev->next != pos)
		{
			posPrev = posPrev->next;
		}

		posPrev->next = newnode;
		newnode->next = pos;
	}
}

 

Delete at specified location  

Here, you can delete at the specified location instead of before or after, because you will encounter some difficulties in header deletion and tail deletion.

//Delete at specified location
void SListErase(SListNode** pphead, SListNode* pos)
{
	assert(pphead && pos);
	if (*pphead == pos)//If the head node is the node to be deleted
	{
		*pphead = (*pphead)->next;
		free(pos);
		pos = NULL;
	}
	else
	{
		SListNode* cur = *pphead;
		while (cur->next != pos)//Find the node to delete
		{
			cur = cur->next;
		}
		cur->next = pos->next;//Point the next of the previous node of the node to be deleted to the next node to be deleted
		free(pos);
		pos = NULL;
	}
}

lookup

According to the data provided, traverse each node in the linked list. If the data in a node is the same, return the address of the node; NULL if not found.

//lookup
SListNode* SListFind(SListNode* phead, SLTDataType x)
{
	while (phead)
	{
		if (phead->data == x)
		{
			return phead;
		}
		phead = phead->next;
	}
	return NULL;
}

Destroy linked list

Save the address of the next node, release the current node, point the pointer to the next node, and release the next node until the linked list is empty.

//Destroy linked list
void SListDestory(SListNode** pphead)
{
    assert(pphead);
	while (*pphead)
	{
		SListNode* next = (*pphead)->next;
		free(*pphead);
		*pphead = next;
	}
}

Complete code

//Print linked list
void SListPrint(SListNode* phead)
{
	SListNode* cur = phead;
	while (cur)
	{
		printf("%d->", cur->data);
		cur = cur->next;
	}
	printf("NULL\n");
}


//Application node
SListNode* SListBuyNode(SLTDataType x)
{
	SListNode* newnode = (SListNode*)malloc(sizeof(SListNode));
	if (newnode == NULL)
	{
		perror("malloc:");
		exit(-1);
	}
	newnode->data = x;
	newnode->next = NULL;
	return newnode;
}

//Destroy linked list
void SListDestory(SListNode** pphead)
{
	assert(pphead);
	SListNode* cur = *pphead;
	while (cur)
	{
		SListNode* next = cur->next;
		free(cur);
		cur = next;
	}
	*pphead = NULL;
}

//Tail insertion
void SListPushBack(SListNode** pphead, SLTDataType x)
{
	assert(pphead);
	SListNode* newnode = SListBuyNode(x);
	if (*pphead == NULL)
	{
		*pphead = newnode;
	}
	else
	{
		SListNode* cur = *pphead;
		while (cur->next)
		{
			cur = cur->next;
		}
		cur->next = newnode;
	}
}

//Head insert
void SListPushFront(SListNode** pphead, SLTDataType x)
{
	assert(pphead);
	SListNode* newnode = SListBuyNode(x);
	newnode->next = *pphead;
	*pphead = newnode;
}

//Tail deletion
void SListPopBack(SListNode** pphead)
{
	assert(*pphead && pphead);
	if ((*pphead)->next == NULL)
	{
		free(*pphead);
		*pphead = NULL;
		return;
	}
	SListNode* cur = *pphead;
	SListNode* next = (*pphead)->next;
	while (next->next)
	{
		next = next->next;
		cur = cur->next;
	}
	cur->next = NULL;
	free(next);
	next = NULL;
}

//Header deletion
void SListPopFront(SListNode** pphead)
{
	assert(*pphead && pphead);
	SListNode* next = (*pphead)->next;
	free(*pphead);
	*pphead = next;
}


//lookup
SListNode* SListFind(SListNode* phead, SLTDataType x)
{
	while (phead)
	{
		if (phead->data == x)
		{
			return phead;
		}
		phead = phead->next;
	}
	return NULL;
}

//Insert after specified position
void SListInsert(SListNode** pphead, SListNode* pos, SLTDataType x)
{
	assert(pphead && pos);
	SListNode* newnode = SListBuyNode(x);
	SListNode* next = pos->next;
	pos->next = newnode;
	newnode->next = next;

}

//Delete at specified location
void SListErase(SListNode** pphead, SListNode* pos)
{
	assert(pphead && pos);
	if (*pphead == pos)
	{
		*pphead = (*pphead)->next;
		free(pos);
		pos = NULL;
	}
	else
	{
		SListNode* cur = *pphead;
		while (cur->next != pos)
		{
			cur = cur->next;
		}
		cur->next = pos->next;
		free(pos);
		pos = NULL;
	}
}

Note: assert(*pphead) and assert(pphead) in the code have different meanings!!!

assert(*pphead) indicates that the linked list is not empty.

assert(pphead) means that the secondary pointer of the parameter cannot be null, because the null pointer cannot be dereferenced!

Force buckle linked list OJ

Force buckle --- remove linked list elements

Idea:

Similar to the tail deletion of a single linked list, first find the element to be deleted, and point the next of the previous node to the next of the deleted node,

Then free deletes the current node.

Of course, there are three situations:

1. The linked list is empty and NULL is returned.
2. The node to be deleted is the head node. Release the head node directly and take the next node as the head node.
3. If the node to be deleted is in, use the conventional method.

The code is as follows:

typedef struct ListNode ListNode;//Rename for easy handling
struct ListNode* removeElements(struct ListNode* head, int val){
    //1. If the linked list is empty, NULL will be returned directly
    if(head == NULL)
    {
        return NULL;
    }

    //Linked list is not empty
    ListNode*cur =head;//Mark nodes to be deleted
    ListNode*prev = NULL;//Mark the previous node of the node to be deleted
    while(cur)
    {
        //Find the node to delete
        if(cur->val==val)
        {
            //2. If the node to be deleted is the head node
            if(cur == head)
            {
                //Point the header pointer to the second node
                head = head->next;
                //Release header node
                free(cur);
                cur = head;
            }
            //3. The node to be deleted is in the middle
            else
            {
                //Point the next of the previous node to the next of the deleted node
                prev->next = cur->next;
                free(cur);
                cur = prev->next;
            }
        }
        //You don't need to delete nodes to move backward
        else
        {
            prev = cur;
            cur = cur->next;
        }
    }
    
    return head;
}

Difference between sequential list and linked list

difference	Sequence table	Linked list
On storage space	Physically continuous	Logically continuous, but not necessarily physically Continued
Random access	Support O(1)	Unsupported: O(N)
Insert or delete element at any position element	May need to move elements, inefficient O(N)	Just modify the pointer
insert	Dynamic sequential table needs to be expanded when space is insufficient Allow	There is no concept of capacity
Application scenario	Element efficient storage + frequent access	Frequent insertion and deletion at any location
Cache utilization	high	low