ENet: A Deep Neural Network Architecture for Real-Time Semantic Segmentation

Paszke, A., Chaurasia, A., Kim, S., & Culurciello, E. (2016). ENet: A Deep Neural Network Architecture for Real-Time Semantic Segmentation. ArXiv, abs/1606.02147.

  # Initial block of the model:
  #         Input
  #        /     \
  #       /       \
  #maxpool2d    conv2d-3x3
  #       \       /  
  #        \     /
  #      concatenate


 # Upsampling bottleneck:
  #     Bottleneck Input
  #        /        \
  #       /          \
  # conv2d-1x1     convTrans2d-1x1
  #      |             | PReLU
  #      |         convTrans2d-3x3
  #      |             | PReLU
  #      |         convTrans2d-1x1
  #      |             |
  # maxunpool2d    Regularizer
  #       \           /  
  #        \         /
  #      Summing + PReLU
  #
  #  Params: 
  #  projection_ratio - ratio between input and output channels
  #  relu - if True: relu used as the activation function else: Prelu us used



  # Regular|Dilated|Downsampling bottlenecks:
  #
  #     Bottleneck Input
  #        /        \
  #       /          \
  # maxpooling2d   conv2d-1x1
  #      |             | PReLU
  #      |         conv2d-3x3
  #      |             | PReLU
  #      |         conv2d-1x1
  #      |             |
  #  Padding2d     Regularizer
  #       \           /  
  #        \         /
  #      Summing + PReLU
  #
  # Params: 
  #  dilation (bool) - if True: creating dilation bottleneck
  #  down_flag (bool) - if True: creating downsampling bottleneck
  #  projection_ratio - ratio between input and output channels
  #  relu - if True: relu used as the activation function else: Prelu us used
  #  p - dropout ratio



  # Asymetric bottleneck:
  #
  #     Bottleneck Input
  #        /        \
  #       /          \
  #      |         conv2d-1x1
  #      |             | PReLU
  #      |         conv2d-1x5
  #      |             |
  #      |         conv2d-5x1
  #      |             | PReLU
  #      |         conv2d-1x1
  #      |             |
  #  Padding2d     Regularizer
  #       \           /  
  #        \         /
  #      Summing + PReLU
  #
  # Params:    
  #  projection_ratio - ratio between input and output channels

Thesis structure

• Abstract

• Introduction

  The current image segmentation network mainly uses the architecture of VGG16, a large number of parameters and long reasoning time.

  Think about Google's new efficient net network architecture.

• Related Work

  large architectures and numerous parameters

• Network architecture

• Design choices

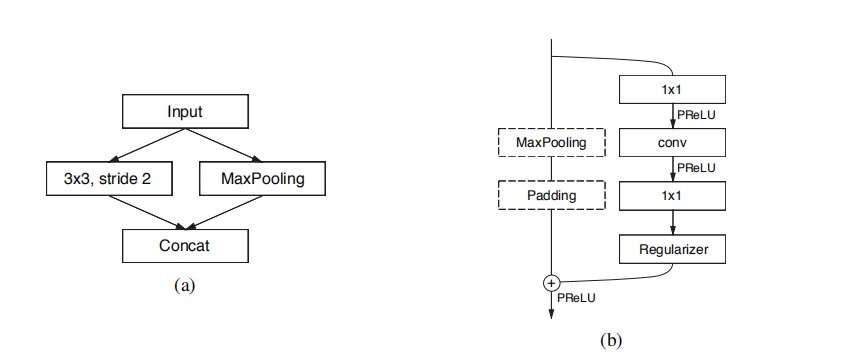
  bottleneck:
  bottleneck sampled below:
  The main line consists of three convolution layers,
  First two × 2. Downsampling of projection;
  Then there is convolution (there are three possibilities, Conv ordinary convolution, asymmetric decomposition convolution, and Dilated hole convolution)
  Followed by a 1 × Note that each convolution layer is followed by Batch
  Norm and PReLU.
  Auxiliary lines include maximum pooling and Padding layers
  Maximum pooling is responsible for extracting context information
  Padding is responsible for filling the channel and connecting the PReLU after the subsequent residual fusion.
  bottleneck without downsampling:
  The main line consists of three convolution layers,
  First 1 × 1 projection;
  Then there is convolution (there are three possibilities, Conv ordinary convolution, asymmetric decomposition convolution, and Dilated hole convolution)
  Followed by a 1 × Note that each convolution layer is followed by Batch
  Norm and PReLU.
  Direct identity mapping of auxiliary lines (only down sampling will increase the number of channels, so the padding layer is not required here)
  Connect PReLU after fusion.

  Feature map resolution: spatial information loss caused by down sampling will affect edge information. The input and output are required to have the same resolution. Strong down sampling also requires strong up sampling. skip connections in FCN; segnet indexes by pooling. In this paper, the input is compressed first, and only a small feature map is input to the network structure to remove the visual redundancy of some pictures. However, the advantage of down sampling is that it can obtain a larger receptive field and more context information for classification.
  The solution of FCN is to plug the feature map in the encoder stage into the decoder to increase spatial information.
  SegNet's solution is to reserve the indexes for downsampling in the encoder stage for upsampling in the decoder stage.
  ENet adopts SegNet method, which can reduce memory requirements. At the same time, in order to increase better context information, we use dilated conv (hole convolution) to expand the context information.

  Post processing modules: CRF and RNN can be used to improve accuracy.

• stage

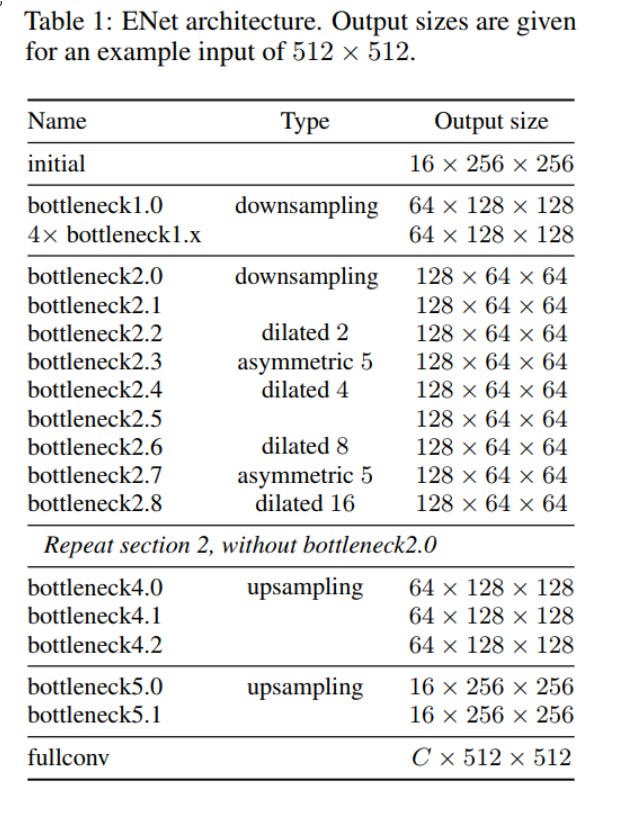
  The ENet model is roughly divided into five stage s:
  -initial: initialize the module
  On the left is do 3 × For the convolution of 3/str=2, MaxPooling is done on the right, concat enate the results on both sides, and merge the channels, which can significantly reduce the storage space.
  -stage1: encoder stage. It includes 5 bottlenecks. The first bottlenecks are sampled, and the next 4 duplicate bottlenecks
  -Stage 2-3: encoder stage. Bottleneck 2.0 of stage 2 does down sampling, followed by hole convolution or decomposition convolution. stage3 has no down sampling. Everything else is the same.
  -Stage 4-5: it belongs to the decoder stage. It's simple. Two ordinary bottleneck s are configured for one upsampling.

• Network architecture

  Early downsampling: early processing of high-resolution input will consume a lot of computing resources, and the initialization model of ENet will greatly reduce the size of input. This is considering that visual information is highly redundant in space and can be compressed into a more effective representation.

  Decoder size: size compared with the mirror symmetry of encoder and decoder in SegNet, the encoder and decoder of ENet are asymmetric and consist of a larger encoder and a smaller decoder.

  Nonlinear operations: relu is not necessarily useful; PRELU. The application of nonlinear activation function relu reduces the accuracy. The reason for analysis is that the number of network layers is too few and not deep enough to filter information quickly. Prelu is used.

  Factorizing filters: n × The convolution kernel of n is split into n × 1 and 1 × N (proposed by inception V3). It can effectively reduce the amount of parameters and improve the receptive field of the model.

  Divided convolutions: void convolution, and the accuracy increases slightly. Cavity convoluted convolutions can effectively improve the receptive field. The effective use of divided revolutions improves the IoU by 4%. The use of divided revolutions is cross use rather than continuous use.

  Regularization: because the data set itself is small, it will be over fitted soon. The effect of using L2 is not good. It's OK to use stochastic depth, but after thinking about it, stochastic depth is a special case of Spatial Dropout. Therefore, the effect of choosing Spatial Dropout is relatively better

  Regularization

• Results

• Conclutison

Reference link: https://github.com/srihari-humbarwadi/ENet-A-Deep-Neural-Network-Architecture-for-Real-Time-Semantic-Segmentation/blob/master/batch_training.py

code

def initial_block(tensor):
    conv = Conv2D(filters=13,kernel_size=(3,3),strides=(2,2),padding="same",name="initial_block_conv",kernel_initializer="he_normal")(tensor)
    pool = MaxPooling2D(pool_size=(2,2),name="initial_blokc_pool")(tensor)
    concat = concatenate([conv,pool],axis=-1,name="initial_block_concat")
    return concat

def bottleneck_encoder(tensor, nfilters, downsampling=False, dilated=False, asymmetric=False, normal=False, drate=0.1,
                       name=''):
    y = tensor
    skip = tensor
    stride = 1
    ksize = 1
    if downsampling:
        stride = 2
        ksize = 2
        skip = MaxPooling2D(pool_size=(2, 2), name=f'max_pool_{name}')(skip)
        skip = Permute((1, 3, 2), name=f'permute_1_{name}')(skip)  # (B, H, W, C) -> (B, H, C, W)
        ch_pad = nfilters - K.int_shape(tensor)[-1]
        skip = ZeroPadding2D(padding=((0, 0), (0, ch_pad)), name=f'zeropadding_{name}')(skip)
        skip = Permute((1, 3, 2), name=f'permute_2_{name}')(skip)  # (B, H, C, W) -> (B, H, W, C)

    y = Conv2D(filters=nfilters // 4, kernel_size=(ksize, ksize), kernel_initializer='he_normal',
               strides=(stride, stride), padding='same', use_bias=False, name=f'1x1_conv_{name}')(y)
    y = BatchNormalization(momentum=0.1, name=f'bn_1x1_{name}')(y)
    y = PReLU(shared_axes=[1, 2], name=f'prelu_1x1_{name}')(y)

    if normal:
        y = Conv2D(filters=nfilters // 4, kernel_size=(3, 3), kernel_initializer='he_normal', padding='same',
                   name=f'3x3_conv_{name}')(y)
    elif asymmetric:
        y = Conv2D(filters=nfilters // 4, kernel_size=(5, 1), kernel_initializer='he_normal', padding='same',
                   use_bias=False, name=f'5x1_conv_{name}')(y)
        y = Conv2D(filters=nfilters // 4, kernel_size=(1, 5), kernel_initializer='he_normal', padding='same',
                   name=f'1x5_conv_{name}')(y)
    elif dilated:
        y = Conv2D(filters=nfilters // 4, kernel_size=(3, 3), kernel_initializer='he_normal',
                   dilation_rate=(dilated, dilated), padding='same', name=f'dilated_conv_{name}')(y)
    y = BatchNormalization(momentum=0.1, name=f'bn_main_{name}')(y)
    y = PReLU(shared_axes=[1, 2], name=f'prelu_{name}')(y)

    y = Conv2D(filters=nfilters, kernel_size=(1, 1), kernel_initializer='he_normal', use_bias=False,
               name=f'final_1x1_{name}')(y)
    y = BatchNormalization(momentum=0.1, name=f'bn_final_{name}')(y)
    y = SpatialDropout2D(rate=drate, name=f'spatial_dropout_final_{name}')(y)

    y = Add(name=f'add_{name}')([y, skip])
    y = PReLU(shared_axes=[1, 2], name=f'prelu_out_{name}')(y)

    return y

def bottleneck_decoder(tensor, nfilters, upsampling=False, normal=False, name=''):
    y = tensor
    skip = tensor
    if upsampling:
        skip = Conv2D(filters=nfilters, kernel_size=(1, 1), kernel_initializer='he_normal', strides=(1, 1),
                      padding='same', use_bias=False, name=f'1x1_conv_skip_{name}')(skip)
        skip = UpSampling2D(size=(2, 2), name=f'upsample_skip_{name}')(skip)

    y = Conv2D(filters=nfilters // 4, kernel_size=(1, 1), kernel_initializer='he_normal', strides=(1, 1),
               padding='same', use_bias=False, name=f'1x1_conv_{name}')(y)
    y = BatchNormalization(momentum=0.1, name=f'bn_1x1_{name}')(y)
    y = PReLU(shared_axes=[1, 2], name=f'prelu_1x1_{name}')(y)

    if upsampling:
        y = Conv2DTranspose(filters=nfilters // 4, kernel_size=(3, 3), kernel_initializer='he_normal', strides=(2, 2),
                            padding='same', name=f'3x3_deconv_{name}')(y)
    elif normal:
        Conv2D(filters=nfilters // 4, kernel_size=(3, 3), strides=(1, 1), kernel_initializer='he_normal',
               padding='same', name=f'3x3_conv_{name}')(y)
    y = BatchNormalization(momentum=0.1, name=f'bn_main_{name}')(y)
    y = PReLU(shared_axes=[1, 2], name=f'prelu_{name}')(y)

    y = Conv2D(filters=nfilters, kernel_size=(1, 1), kernel_initializer='he_normal', use_bias=False,
               name=f'final_1x1_{name}')(y)
    y = BatchNormalization(momentum=0.1, name=f'bn_final_{name}')(y)

    y = Add(name=f'add_{name}')([y, skip])
    y = ReLU(name=f'relu_out_{name}')(y)

    return y

def ENET(input_shape=(None, None, 3), nclasses=11):
    print('. . . . .Building ENet. . . . .')
    img_input = Input(input_shape)

    x = initial_block(img_input)

    x = bottleneck_encoder(x, 64, downsampling=True, normal=True, name='1.0', drate=0.01)
    for _ in range(1, 5):
        x = bottleneck_encoder(x, 64, normal=True, name=f'1.{_}', drate=0.01)

    x = bottleneck_encoder(x, 128, downsampling=True, normal=True, name=f'2.0')
    x = bottleneck_encoder(x, 128, normal=True, name=f'2.1')
    x = bottleneck_encoder(x, 128, dilated=2, name=f'2.2')
    x = bottleneck_encoder(x, 128, asymmetric=True, name=f'2.3')
    x = bottleneck_encoder(x, 128, dilated=4, name=f'2.4')
    x = bottleneck_encoder(x, 128, normal=True, name=f'2.5')
    x = bottleneck_encoder(x, 128, dilated=8, name=f'2.6')
    x = bottleneck_encoder(x, 128, asymmetric=True, name=f'2.7')
    x = bottleneck_encoder(x, 128, dilated=16, name=f'2.8')

    x = bottleneck_encoder(x, 128, normal=True, name=f'3.0')
    x = bottleneck_encoder(x, 128, dilated=2, name=f'3.1')
    x = bottleneck_encoder(x, 128, asymmetric=True, name=f'3.2')
    x = bottleneck_encoder(x, 128, dilated=4, name=f'3.3')
    x = bottleneck_encoder(x, 128, normal=True, name=f'3.4')
    x = bottleneck_encoder(x, 128, dilated=8, name=f'3.5')
    x = bottleneck_encoder(x, 128, asymmetric=True, name=f'3.6')
    x = bottleneck_encoder(x, 128, dilated=16, name=f'3.7')

    x = bottleneck_decoder(x, 64, upsampling=True, name='4.0')
    x = bottleneck_decoder(x, 64, normal=True, name='4.1')
    x = bottleneck_decoder(x, 64, normal=True, name='4.2')

    x = bottleneck_decoder(x, 16, upsampling=True, name='5.0')
    x = bottleneck_decoder(x, 16, normal=True, name='5.1')

    img_output = Conv2DTranspose(nclasses, kernel_size=(2, 2), strides=(2, 2), kernel_initializer='he_normal',
                                 padding='same', name='image_output')(x)
    img_output = Activation('softmax')(img_output)

    model = Model(inputs=img_input, outputs=img_output, name='ENET')
    print('. . . . .Build Compeleted. . . . .')
    return model

Where the loss value is defined

def dice_coeff(y_true, y_pred):
    smooth = 1.
    y_true_f = K.flatten(y_true)
    y_pred_f = K.flatten(y_pred)
    intersection = K.sum(y_true_f * y_pred_f)
    score = (2. * intersection + smooth) / (K.sum(y_true_f) + K.sum(y_pred_f) + smooth)
    return score

def dice_loss(y_true, y_pred):
    loss = 1 - dice_coeff(y_true, y_pred)
    return loss

def total_loss(y_true, y_pred):
    loss = binary_crossentropy(y_true, y_pred) + (3*dice_loss(y_true, y_pred))
    return loss