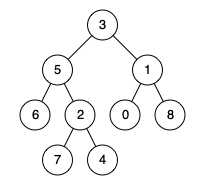
Give you a binary tree and two nodes in the binary tree, and find the nearest common ancestor of the two nodes. Nearest common ancestor: "for two nodes p and q with root tree root, the nearest common ancestor is expressed as a node a, which satisfies that a is the ancestor of p and q, and the depth of a is as large as possible (a node can also be its own ancestor)." for example, the nearest common ancestor of node 6 and node 0 is node 3, and the nearest common ancestor of node 5 and node 4 is node 5.

Title 1: if the tree is a binary search tree.
The nodes in the binary search tree are arranged in order. The value of the left subtree node < the root node < the value of the right subtree node. We can traverse each node from the root node. If the current node is greater than these two nodes, the common ancestor must be in the left subtree of the current node, If the current node is smaller than these two nodes, the common ancestor must be in the right subtree of the current node. Otherwise, the current node is the nearest public ancestor we are looking for.

 TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if(root == NULL) return NULL;

        if(root -> val > p-> val && root -> val > q -> val)
        return lowestCommonAncestor(root -> left,p,q);

        if(root -> val < p -> val && root -> val < q -> val)
        return lowestCommonAncestor(root -> right,p,q);

        return root;
    }

Topic 2: This is an ordinary binary tree, but it has a pointer to the parent node. (except root node)
The red and green nodes on the left in the figure below are the two nodes of the nearest common ancestor we require. The blue line is the pointer to the parent node.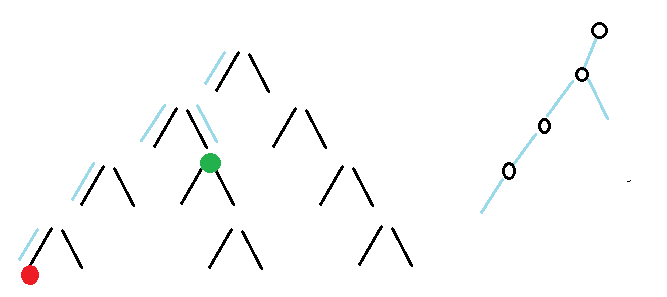
If we abstract the path from the two current nodes to the root node into two linked lists, the nearest common ancestor is the first node of the two intersecting linked lists.

TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q){
	if(root == NULL) return NULL;
	
	stack<TreeNode*>s1;
	stack<TreeNode*>s2;
	TreeNode* p;
	
	while(p -> parent != root){
		s1.push(p);
		p = p -> parent;
	}
	s1.push(p);
	s1.push(p -> parent);

	while(q -> parent != root){
		s2.push(q);
		q = q -> parent;
	}
	s2.push(q);
	s2.push(q -> parent);

	while(!s1.empty() && !s2.empty()){
		if(s1.top() == s2.top()){
			p = s1.top();
			s1.pop();
			s2.pop();
		}
		else
			break;
	}
	return p;
}

Topic 3: This is an ordinary binary tree.
If this is an ordinary binary tree, although we don't have a pointer to the parent node, we can follow the idea of Topic 2. We get the path to the specified node from the root node, and then convert it to find the intersection node of the linked list. It should be noted that this intersection node will be stored at the bottom of the stack, We may need to pop up some nodes to ensure that the elements in the two stacks are equal, and then find the intersection node.

The first and third functions in the following code are easier to write. The core code is how to save the path from the root node to the specified node, that is, the second function.

 TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if(root == NULL || p == NULL || q == NULL)
        return NULL;

        stack<TreeNode*>path1;
        GetNodePath(root,p,path1);

        stack<TreeNode*>path2;
        GetNodePath(root,q,path2);

        return GetLastCommonNode(path1,path2);
        
  }
  
bool GetNodePath(TreeNode* root,TreeNode* pNode,stack<TreeNode*> &path){
        if(root == NULL)
        return false;

        path.push(root); //Save the node currently traversed
        
        if(pNode == root)
        return true;

        if(GetNodePath(root -> left,pNode,path))//Go to the left subtree of the current traversal node to find the specified node
        return true;

        if(GetNodePath(root -> right,pNode,path))//Go to the right subtree of the current traversal node to find the specified node
        return true;

        path.pop(); //If the left and right subtrees of the current node do not find the specified node, the node cannot exist in the path
        return false;
 }
 
TreeNode* GetLastCommonNode(stack<TreeNode*>&path1,stack<TreeNode*>&path2){
       int a = path1.size();
       int b = path2.size();

       if(a > b){
           int c = a-b;
           while(c!= 0){
               path1.pop();
               c--;
           }
       }

        if(a<b){
           int c = b-a;
           while(c != 0){
               path2.pop();
               c--;
           }
       }

       while(!path1.empty() && !path2.empty()){
           if(path1.top() != path2.top()){
               path1.pop();
               path2.pop();
           }
           else
           break;
       }
       return path1.top();
  }