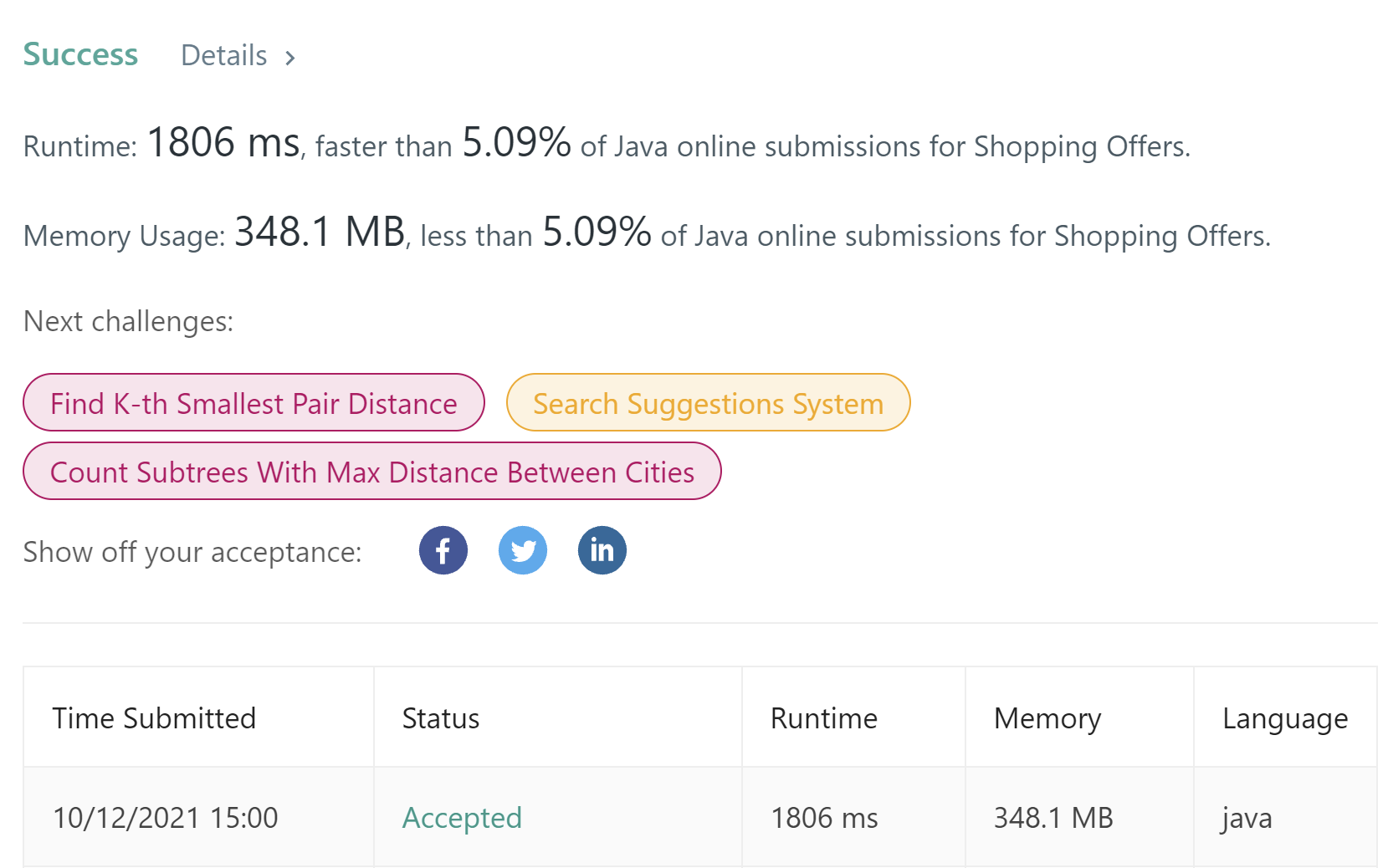
subject

https://leetcode.com/problems/shopping-offers/

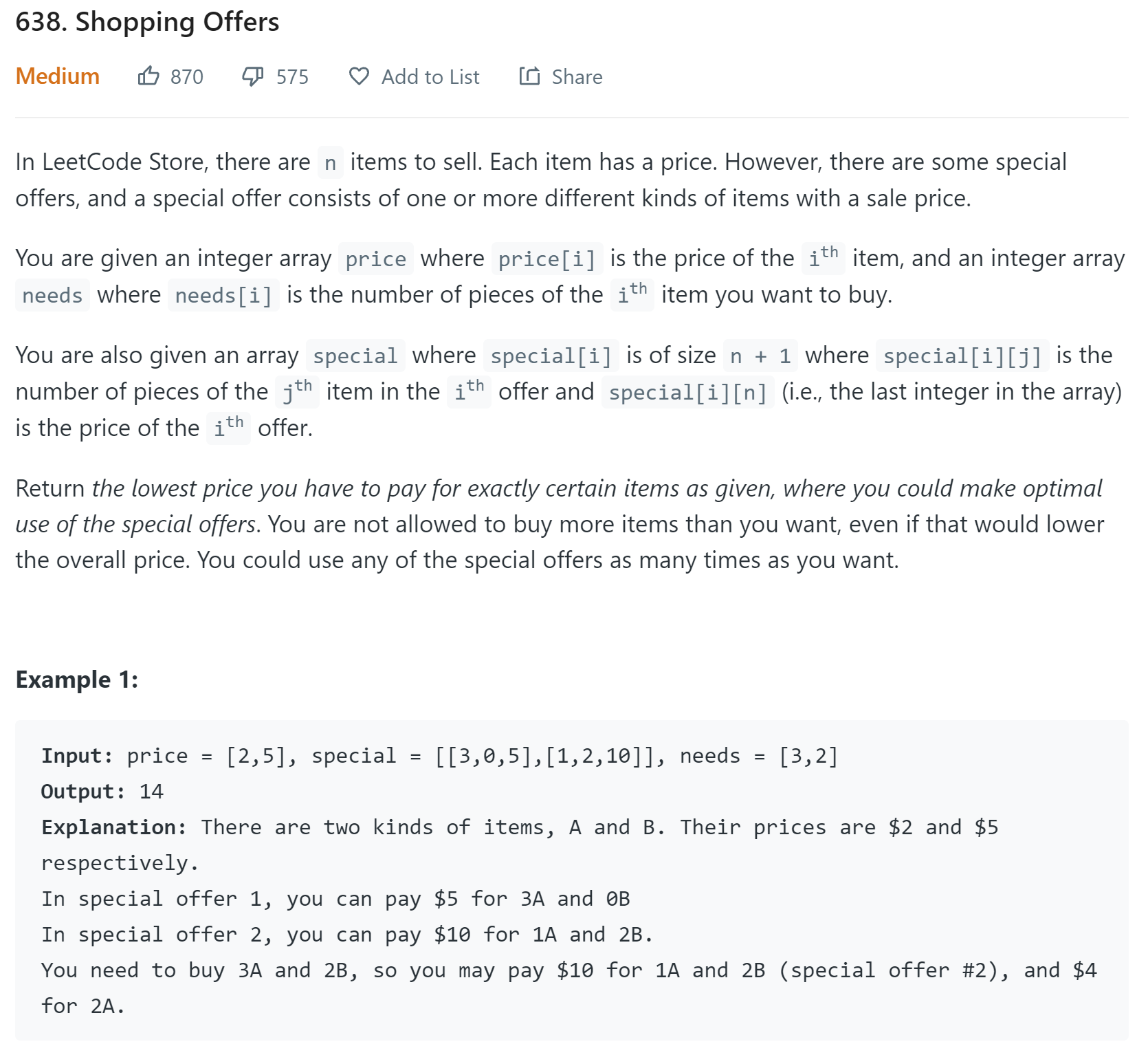
Problem solution

Similar topics include: leetcode 474. Ones and Zeroes | 474. One and zero (double constrained knapsack problem)

This problem is essentially a knapsack problem with multiple constraints (n < 6). The goal is to minimize the total price when the knapsack is just full. Items can be used unlimited times.

Refer to section 19 of Zuoshen system class: clip art problem (actually I didn't refer to it, just thought of such a problem)

Given a string str and an array arr of string type, all characters appear in lowercase English
arr each string represents a sticker. You can cut a single character and use it to spell str
Return at least how much poster paper is needed to complete this task.
Example: str = "babac", arr = {"ba", "c", "abcd"}
ba + ba + c 3 abcd + abcd 2 abcd+ba 2
So this question returns to 2

Because some items are given in the form of combination, we first convert the list nested list into an array to facilitate index search.
Then, because the item can be purchased separately. For the sake of unification and convenience, we also convert the items that can be purchased separately into the form of combination, but let their coefficients be 1.

As shown in the figure below, the first two lines are the prices for separately purchasing item A and item B, and the last two lines are the prices for the combination of items AB.

Then there is the classic violent recursion - > silly cache. This problem should not be converted to dp because there are too many states. See the key in dp map for details. My processing method is to compress the state into a string. Later, I found that hashmap can directly use list as the key.

In addition, my efficiency is extremely low (it should be that I have a large array cost of copy to avoid backtracking). If I delete the import header file, it will timeout (this is also the honey feature of leetcode. If I take the lead file, it will run faster). I can AC with the header file.

import java.util.HashMap;
import java.util.List;
import java.util.Map;

class Solution {
    int M; // Total packages
    int N; // Total items

    public int shoppingOffers(List<Integer> price, List<List<Integer>> special, List<Integer> needs) {
        N = price.size();
        M = special.size() + price.size();

        // Array package list
        int[][] sp = new int[M][N + 1];
        for (int i = 0; i < special.size(); i++) {
            List<Integer> list = special.get(i);
            for (int j = 0; j < N + 1; j++) {
                sp[i][j] = list.get(j);
            }
        }
        for (int i = special.size(), j = 0; i < M; i++, j++) {
            sp[i][j] = 1;
            sp[i][N] = price.get(j);
        }

        // Array shopping list
        int[] need = new int[N];
        for (int i = 0; i < N; i++) {
            need[i] = needs.get(i);
        }
        
        Map<String, Integer> dp = new HashMap<>();
        return process(sp, need, 0, dp);
    }

    // Multi constrained knapsack problem
    // The list of items is in special. How much cost does the currently selectable items need when they are in the cur position and there are still needs to buy
    public int process(int[][] special, int[] needs, int cur, Map<String, Integer> dp) {
        // Cache lookup
        StringBuilder key = new StringBuilder();
        for (int n : needs) { // The state is compressed into a string
            key.append(n).append(":");
        }
        key.append(cur);
        if (dp.containsKey(key.toString())) return dp.get(key.toString());

        if (allZero(needs)) {
            dp.put(key.toString(), 0);
            return 0;
        }

        int minCost = Integer.MAX_VALUE;
        for (int p = cur; p < M; p++) { // Current purchase of special[p] package
            for (int count = 0; canBuy(special, needs, count, p); count++) { // Purchase count p package
                int[] newNeeds = buy(special, needs, count, p);
                int newCost = process(special, newNeeds, p + 1, dp);
                if (newCost != Integer.MAX_VALUE) {
                    minCost = Math.min(minCost, count * special[p][N + 1 - 1] + newCost);
                }
            }
        }
        // cache
        dp.put(key.toString(), minCost);

        return minCost;
    }

    // In the current state, if you continue to buy count p items, do you buy unnecessary items
    public boolean canBuy(int[][] special, int[] needs, int count, int p) {
        for (int k = 0; k < N; k++) {
            if (needs[k] - count * special[p][k] < 0) return false;
        }
        return true;
    }

    public int[] buy(int[][] special, int[] needs, int count, int p) {
        int[] newNeeds = new int[N];
        for (int k = 0; k < N; k++) {
            newNeeds[k] = needs[k] - count * special[p][k];
        }
        return newNeeds;
    }

    public boolean allZero(int[] needs) {
        for (int n : needs) {
            if (n != 0) return false;
        }
        return true;
    }

}