13.1 basic introduction

13.1.1 why is there a diagram

1. We learned linear tables and trees earlier
2. The linear table is limited to the relationship between a direct precursor and a direct successor
3. The tree can only have one direct precursor, that is, the parent node
4. When we need to represent many to many relationships, we use graphs here

13.1.2 illustration of figure

A graph is a data structure in which a node can have zero or more adjacent elements. The connection between two nodes is called an edge. Nodes can also be called vertices. As shown in the figure:

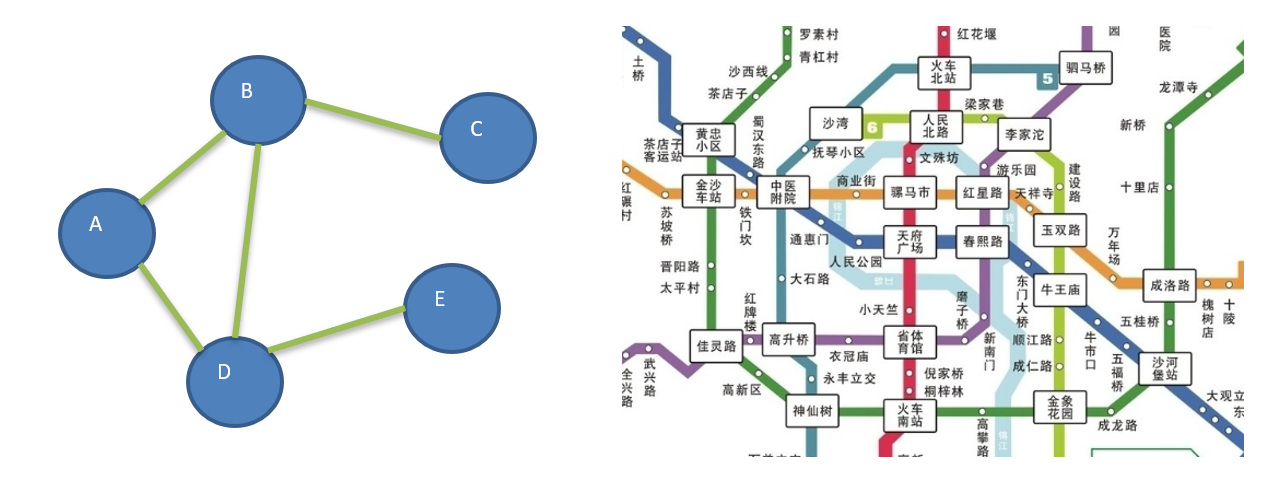
13.1.3 common concepts of drawings

1. Vertex
2. Edge
3. route
4. Undirected graph (below)

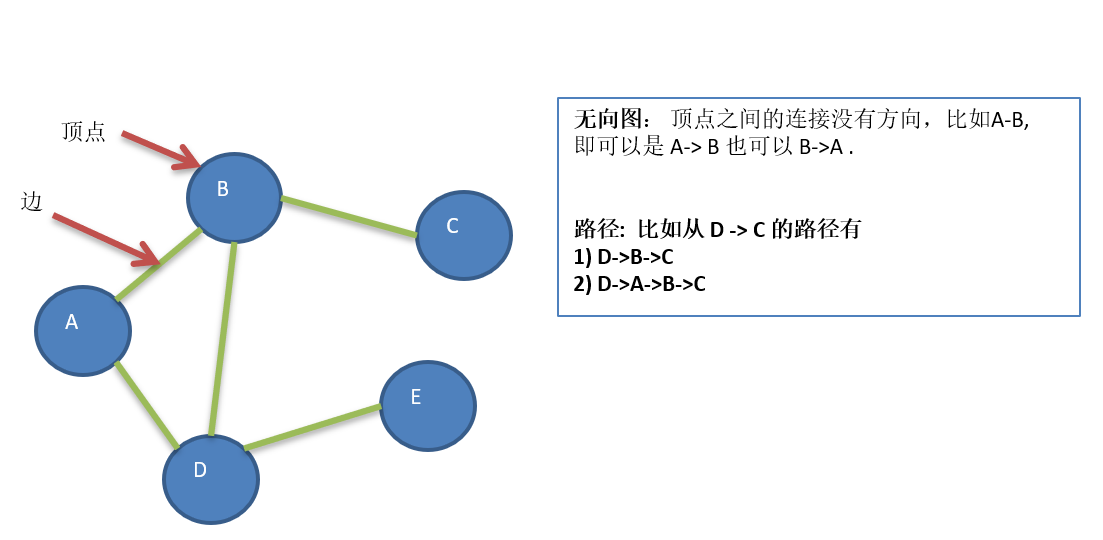
1. Directed graph
2. Weighted graph

13.2 representation of drawings

There are two representations of graphs: two-dimensional array representation (adjacency matrix); Linked list representation (adjacency list).

13.2.1 adjacency matrix

Adjacency matrix is a matrix that represents the adjacency relationship between vertices in a graph. For a graph with n vertices, row and col represent 1... N points.

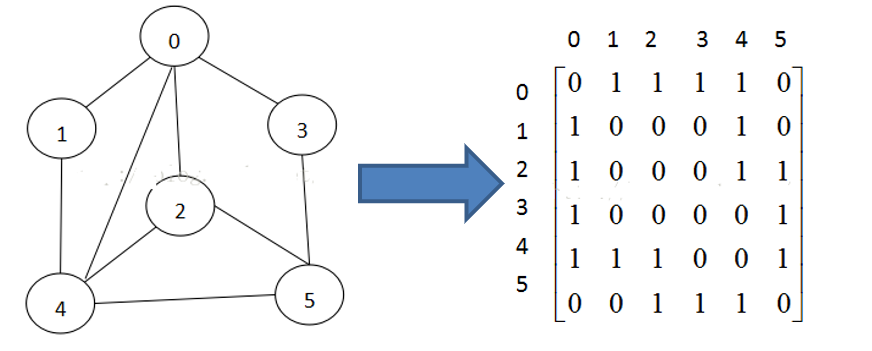
13.2.2 adjacency table

1. Adjacency matrix needs to allocate n edge spaces for each vertex. In fact, many edges do not exist, which will cause a certain loss of space.
2. The implementation of adjacency table only cares about the existing edges, not the nonexistent edges. Therefore, there is no space waste. The adjacency table is composed of array + linked list
3. Examples
   

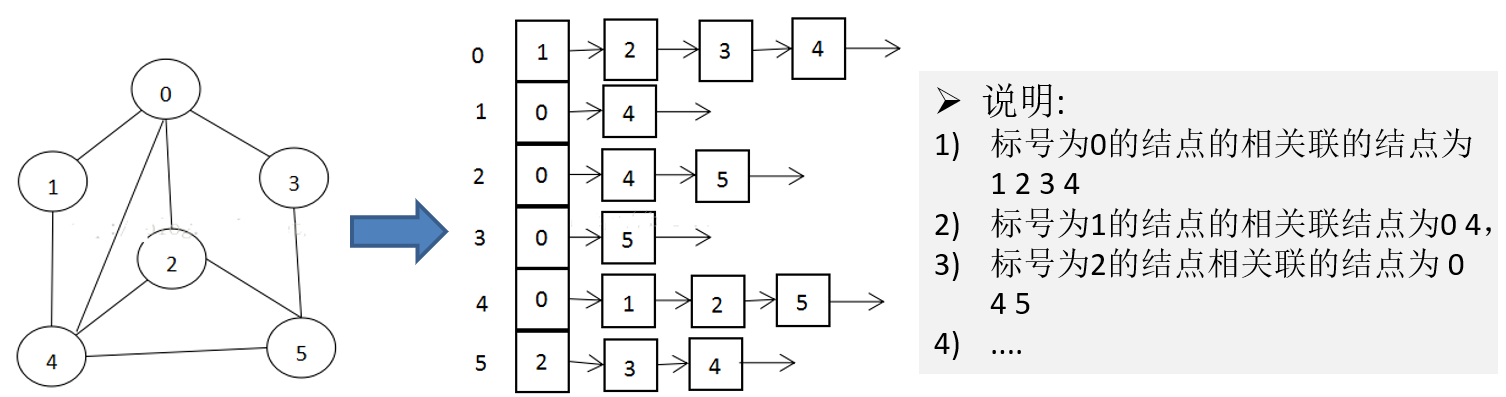
Figure 13.3 quick start case

1. Requirements: the code implementation is shown in the following figure.

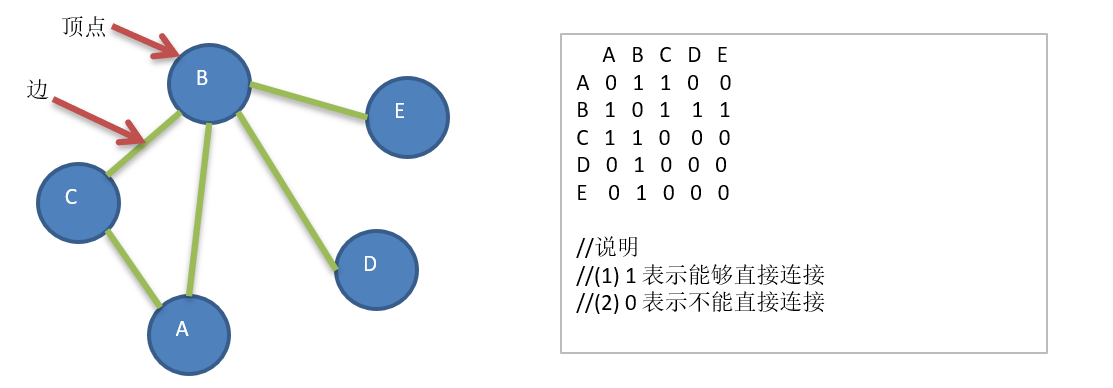
1. Train of thought analysis

(1) Storing vertex strings using ArrayList
(2) Save matrix int[][] edges

1. code implementation

//Summarized later
//Insert Knot 
public void insertVertex(String vertex) {
    vertexList.add(vertex);
}
//Add edge
/**
 *
 * @param v1 Indicates the subscript of the point, even if the vertex "a" - "B", "a" - > 0 "B" - > 1
 * @param v2 Subscript corresponding to the second vertex
 * @param weight express
 */
public void insertEdge(int v1, int v2, int weight) {
    edges[v1][v2] = weight;
    edges[v2][v1] = weight;
    numOfEdges++;
}

13.4 introduction to depth first traversal of figure

Figure 13.4.1 introduction to traversal

The so-called graph traversal is the access to nodes. There are so many nodes in a graph. How to traverse these nodes requires specific policies. Generally, there are two access policies:
(1) Depth first traversal
(2) Breadth first traversal

13.4.2 basic idea of depth first traversal

Depth first search of graph.

1. Depth first traversal: starting from the initial access node, the initial access node may have multiple adjacent nodes. The strategy of depth first traversal is to first access the first adjacent node, and then use the accessed adjacent node as the initial node to access its first adjacent node, It can be understood as follows: after accessing the current node every time, first access the first adjacent node of the current node.
2. We can see that such an access strategy gives priority to vertical mining, rather than horizontal access to all adjacent nodes of a node.
3. Obviously, depth first search is a recursive process

13.4.3 depth first traversal algorithm steps

1. Access the initial node v and mark node v as accessed.
2. Find the first adjacent node w of node v.
3. If w exists, continue with 4. If w does not exist, return to step 1 and continue from the next node of v.
4. If W is not accessed, perform depth first traversal recursion on w (that is, treat w as another v, and then proceed to step 123).
5. Find the next adjacent node of the w adjacent node of node v and go to step 3.
6. Analysis diagram
   

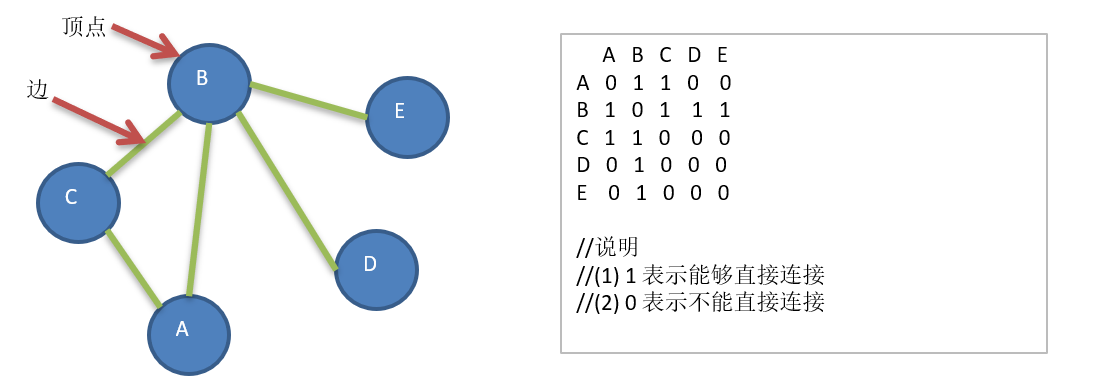
13.4.4 code implementation of depth first algorithm

//Summarized later
//Depth first traversal algorithm
//i is 0 for the first time
private void dfs(boolean[] isVisited, int i) {
     //First, we access the node and output
    System.out.print(getValueByIndex(i) + "->");
     //Set the node as accessed
    isVisited[i] = true;
    //Find the first adjacent node w of node i
    int w = getFirstNeighbor(i);
    while(w != -1) {//Description yes
        if(!isVisited[w]) {
            dfs(isVisited, w);
        }
        //If the w node has been accessed
        w = getNextNeighbor(i, w);
    }
}
//Carry out an overload on dfs, traverse all our nodes, and perform dfs
public void dfs() {
    isVisited = new boolean[vertexList.size()];
    //Traverse all nodes and perform dfs [backtracking]
    for(int i = 0; i < getNumOfVertex(); i++) {
        if(!isVisited[i]) {
            dfs(isVisited, i);
        }
    }
}

13.5 breadth first traversal of Graphs

13.5.1 basic idea of breadth first traversal

1. Broad first search of graph.
2. Similar to a hierarchical search process, breadth first traversal needs to use a queue to maintain the order of visited nodes, so as to access the adjacent nodes of these nodes in this order

13.5.2 breadth first traversal algorithm steps

1. Access the initial node v and mark node v as accessed.
2. Node v in queue
3. When the queue is not empty, continue to execute, otherwise the algorithm ends.
4. Out of the queue, get the queue head node u.
5. Find the first adjacent node w of node u.
6. If the adjacent node w of node u does not exist, go to step 3; Otherwise, the loop performs the following three steps:

6.1 if node w has not been accessed, access node W and mark it as accessed.
6.2 node w in queue
6.3 find the next adjacent node w of node u after the adjacent node W, and go to step 6.

13.5.3 diagram of breadth first algorithm

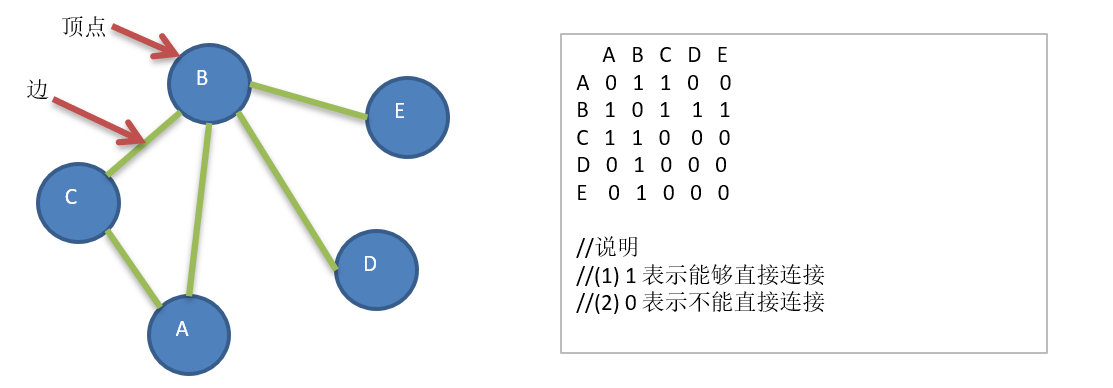
13.6 code implementation of breadth first algorithm

//Summarized later
//A method of breadth first traversal of a node
private void bfs(boolean[] isVisited, int i) {
    int u; // Indicates the subscript corresponding to the head node of the queue
    int w; // Adjacent node w
    //Queue, which records the access order of nodes
    LinkedList queue = new LinkedList();
    //Access node and output node information
    System.out.print(getValueByIndex(i) + "=>");
    //Mark as accessed
    isVisited[i] = true;
    //Add node to queue
    queue.addLast(i);
    while (!queue.isEmpty()) {
        //Fetch the subscript of the header node of the queue
        u = (Integer) queue.removeFirst();
        //Get the subscript w of the first adjacent node
        w = getFirstNeighbor(u);
        while (w != -1) {//find
            //Have you visited
            if (!isVisited[w]) {
                System.out.print(getValueByIndex(w) + "=>");
                //Mark already accessed
                isVisited[w] = true;
                //Join the team
                queue.addLast(w);
            }
            //Take u as the precursor point and find the next neighbor node after w
            w = getNextNeighbor(u, w); //Reflect our breadth first
        }
    }
}

//Traverse all nodes and perform breadth first search
public void bfs() {
    isVisited = new boolean[vertexList.size()];
    for (int i = 0; i < getNumOfVertex(); i++) {
        if (!isVisited[i]) {
            bfs(isVisited, i);
        }
    }
}

13.7 code summary of figure

import java.util.ArrayList;
import java.util.Arrays;
import java.util.LinkedList;
import java.util.List;

/**
 * @author zk
 * @version 1.0.0
 * @ClassName Grap.java
 * @Description TODO Graph (depth first traversal and breadth first traversal)
 * @createTime 2021 17:05:00, September 28
 */
public class Graph {
    private List<String> vertexList; // Store the vertices of the graph
    private int[][] edges; // Store the adjacency matrix corresponding to the graph
    private int numOfEdges; // Indicates the number of edges
    boolean[] isVisited; // Indicates whether the vertices corresponding to the following table have been traversed


    public static void main(String[] args) {

        String[] vertexs = {"A", "B", "C", "D", "E"};
        Graph graph = new Graph(vertexs.length);
        for (String vertex : vertexs) {
            graph.insertVertex(vertex);
        }
        graph.insertEdge(0, 1, 1);
        graph.insertEdge(0, 2, 1);
        graph.insertEdge(1, 2, 1);
        graph.insertEdge(1, 3, 1);
        graph.insertEdge(1, 4, 1);
        graph.showGraph();
        //graph.dfs();
        graph.bfs();
    }

    // Parametric structure
    public Graph(int n) {
        this.vertexList = new ArrayList<>(n);
        this.edges = new int[n][n];
        this.numOfEdges = 0;
        this.isVisited = new boolean[n];
    }

    // Insert node
    public void insertVertex(String vertex) {
        vertexList.add(vertex);
    }

    // Add edge
    public void insertEdge(int v1, int v2, int weight) {
        this.edges[v1][v2] = weight;
        this.edges[v2][v1] = weight;
        this.numOfEdges++;
    }

    // Returns the number of vertices
    public int getNumOdVertex() {
        return this.vertexList.size();
    }

    // Returns the number of edges
    public int getNumOfEdge() {
        return this.numOfEdges;
    }

    // Return the data 0 - > a 1 - > b corresponding to node i (subscript)
    public String getValueByIndex(int i) {
        return this.vertexList.get(i);
    }

    // Returns the weight of v1 v2
    public int getWeight(int v1, int v2) {
        return edges[v1][v2];
    }

    // Display the matrix corresponding to the figure
    public void showGraph() {
        for (int[] link : edges) {
            System.out.println(Arrays.toString(link));
        }
    }

    //Get the subscript w of the first adjacent node
    /**
     *
     * @param index
     * @return If it exists, it returns the corresponding subscript; otherwise, it returns - 1
     */
    public int getFirstNeighbor(int index){
        for (int i = 0; i < vertexList.size(); i++) {
            if (edges[index][i]>0){
                return i;
            }
        }
        // non-existent
        return -1;
    }

    //The next adjacent node is obtained according to the subscript of the previous adjacent node
    public int getNextNeighbor(int v1,int v2){
        for (int i = v2 + 1; i < vertexList.size(); i++) {
            if (edges[v1][i]>0){
                return i;
            }
        }
        return -1;
    }

    //Depth first traversal algorithm
    //i the first time
    public void dfs(boolean[] isVisited,int i){
        System.out.print(getValueByIndex(i)+"->");
        isVisited[i] = true;
        int w = getFirstNeighbor(i);
        while (w!=-1){
            if(!isVisited[w]){
                dfs(isVisited,w);
            }
            w = getNextNeighbor(i,w);
        }
    }


    //Carry out an overload on dfs, traverse all our nodes, and perform dfs
    public void dfs(){
        for (int i = 0; i < vertexList.size(); i++) {
            if (!isVisited[i]){
                dfs(this.isVisited,i);
            }
        }

    }

    //A method of breadth first traversal of a node
    public void bfs(boolean[] isVisited,int i){

        int u; // Indicates the subscript corresponding to the head node of the queue
        int w; // Adjacent node w
        //Queue, which records the access order of nodes
        LinkedList<Integer> queue = new LinkedList<>();

        System.out.print(getValueByIndex(i)+"=>");
        isVisited[i] = true;
        queue.addLast(i);
        while (!queue.isEmpty()){
            u = queue.removeFirst();
            w = getFirstNeighbor(u);
            while (w!=-1){
                if (!isVisited[w]){
                    System.out.print(getValueByIndex(w)+"=>");
                    isVisited[w] = true;
                    queue.addLast(w);
                }
                w = getNextNeighbor(u,w);
            }
        }
    }

    public void bfs(){
        for (int i = 0; i < vertexList.size(); i++) {
            if (!isVisited[i]){
                bfs(isVisited,i);
            }
        }
    }


}