Bubble sorting and its optimization
Basic idea of bubble sorting
1. Access each element of the array from scratch and exchange between adjacent elements
2. Exchange elements in pairs. Change the small one to the front and the large one to the back.
3. After all elements are exchanged, one exchange is completed, and the largest element will reach the end of the array.
4. Repeat the above steps until all elements are sorted.
End condition: no exchange occurs during any trip.
Note: the bubbling algorithm controls the number of runs and the elements to be compared in each run through double loops, that is, the outer loop controls the number of runs and the inner loop controls the number of elements to be compared.
The worst case of a trip is to arrange one element, so n elements need n trips. Because the last element is left, the order has been arranged, so n - 1 trip is required at last.
Programming idea: when there is no idea to solve a certain kind of problem, it can be analyzed with the help of examples.
eg: in bubble sorting, when the judgment condition of j is not known, the instance can be analyzed. There are 10 elements in the first round,
Exchange 10 - 1 times. There are 10 elements in the second round. Exchange 10 - 1 - J (at this time, j is 1) = 8,
The code is inversely derived from the results.
// Bubble sorting
public static void bubbleSort(int[] arr) {
for (int i = 0; i < arr.length - 1; i++) {// Number of rounds
for (int j = 0; j < arr.length - i - 1; j++) {// frequency
if (arr[j] > arr[j + 1]) {
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
}
Optimization 1:
Suppose we now sort the group of data arr [] = {1, 2, 3, 4, 5, 6, 7, 9, 8}. According to the above sorting method, 8 and 9 have been exchanged in order after the first sorting. The next sorting is redundant and nothing is done. So we
You can add a mark at the place of exchange. If there are no exchange elements in that sort, it indicates that the group of data has been ordered and does not need to continue.
// Bubble sorting optimization I: sequential and overall disorder, eg:{1,2,3,4,5,7,6}
public static void bubbleSort1(int[] arr) {
boolean flag = true;// Define a flag to monitor whether an exchange occurs in a round
for (int i = 0; i < arr.length - 1; i++) {
for (int j = 0; j < arr.length - i - 1; j++) {
if (arr[j] > arr[j + 1]) {
flag = false;
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
if (flag) {
break;
}
}
}Optimization II:
Optimization 1 is only applicable to contiguous ordered and overall disordered data (e.g. 1, 2, 3, 4, 5, 7, 6). However, the sorting efficiency of most of the data (1, 2, 5, 7, 4, 3, 6, 8, 9, 10) in the front is not optimistic, and we can continue to optimize this data type. That is, we can write down the position of the last exchange. If there is no exchange behind, it must be orderly, and then the next sort will be compared from the first reach Last recorded position Until the end.
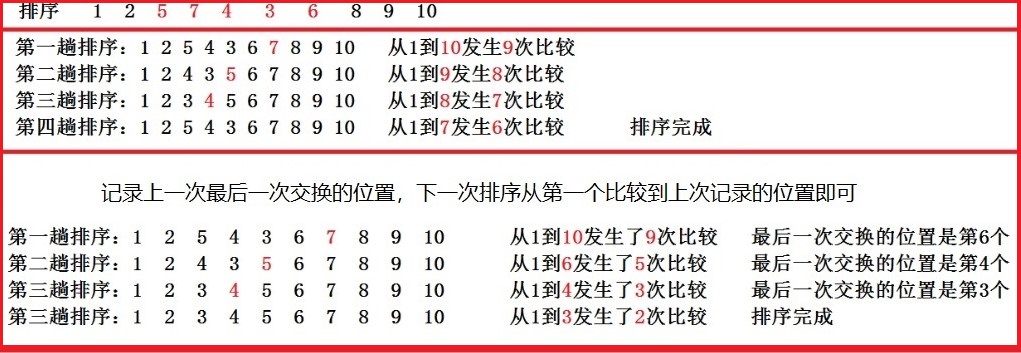
Note: the second optimization does not need to use flag, which is redundant. If the last exchange position is 0, it has been explained that there is no exchange
// Bubble sorting optimization 2: most of the front parts are disordered while the back part is orderly, eg:{1,2,5,7,4,3,6,8,9,10}
public static void bubbleSort2(int[] arr) {
for (int i = 0; i < arr.length - 1; i++) {// Number of rounds
int end = arr.length - 1;
int pos = 0;// Record the position of the last exchange in a round
for (int j = 0; j < end; j++) {// frequency
if (arr[j] > arr[j + 1]) {
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
pos = j;
}
}
end = pos;// Just compare to the record position next time
}
}
Optimization III:
Two way bubble sorting, also known as cocktail sorting: its process is: first compare once from left to right, then compare once from right to left, then compare once from left to right, and so on.
Advantages: it can reduce the number of rounds sorted under specific conditions; Disadvantages: double the amount of code. Usage scenario: when most elements have been ordered.
It is used to optimize arrays in which most of the previous elements have been ordered. For example, for arrays [2,3,4,5,6,7,8,1], if ordinary bubble sorting is used, it needs to be compared seven times; Instead of two-way bubble sorting, you only need to compare it three times.
For simplicity, let's take a look at the simple two-way bubble sorting (without combining the previous two optimizations):
// Bubble sorting optimization III (bidirectional bubble sorting): when most elements have been ordered. {2,3,4,5,6,7,8,1}
public static void bubbleSort3(int[] arr) {
int temp = 0;
for (int i = 0; i < arr.length / 2; i++) {
// Odd wheel, compare and exchange from left to right
for (int j = i; j < arr.length - 1; j++) {
if (arr[j] > arr[j + 1]) {
temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
// Even wheel, compare and exchange from right to left
for (int j = arr.length - i - 1; j > i; j--) {
if (arr[j] < arr[j - 1]) {
temp = arr[j];
arr[j] = arr[j - 1];
arr[j - 1] = temp;
}
}
}Final optimization: optimization I + optimization II + optimization III
// Final optimization: mode 1 + mode 2 + mode 3
public static void bubbleSort4(int[] arr) {
int temp = 0;
boolean flag = true;// sign
int leftEnd = 0;// The left boundary of the unordered sequence. Each comparison only needs to be compared so far
int rightEnd = arr.length - 1;// The right boundary of the unordered sequence. Each comparison only needs to be compared so far
int posLeft = 0;// Record the position of the last exchange on the left
int posRight = 0;// Record the position of the last exchange on the right
for (int i = 0; i < arr.length / 2; i++) {
// Odd rounds, switching from left to right
for (int j = leftEnd; j < rightEnd; j++) {
if (arr[j] > arr[j + 1]) {
temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
flag = false;
posRight = j;
}
}
rightEnd = posRight;
if (flag) {
break;
}
flag = true;// Flag reset!!!!!!!!!!!!!!!!!!!!!!!!!
// Even wheels, switching from right to left
for (int j = rightEnd; j > leftEnd; j--) {
if (arr[j] < arr[j - 1]) {
temp = arr[j];
arr[j] = arr[j - 1];
arr[j - 1] = temp;
flag = false;
posLeft = j;
}
}
leftEnd = posLeft;
if (flag) {
break;
}
}
}Quick sort and its optimization
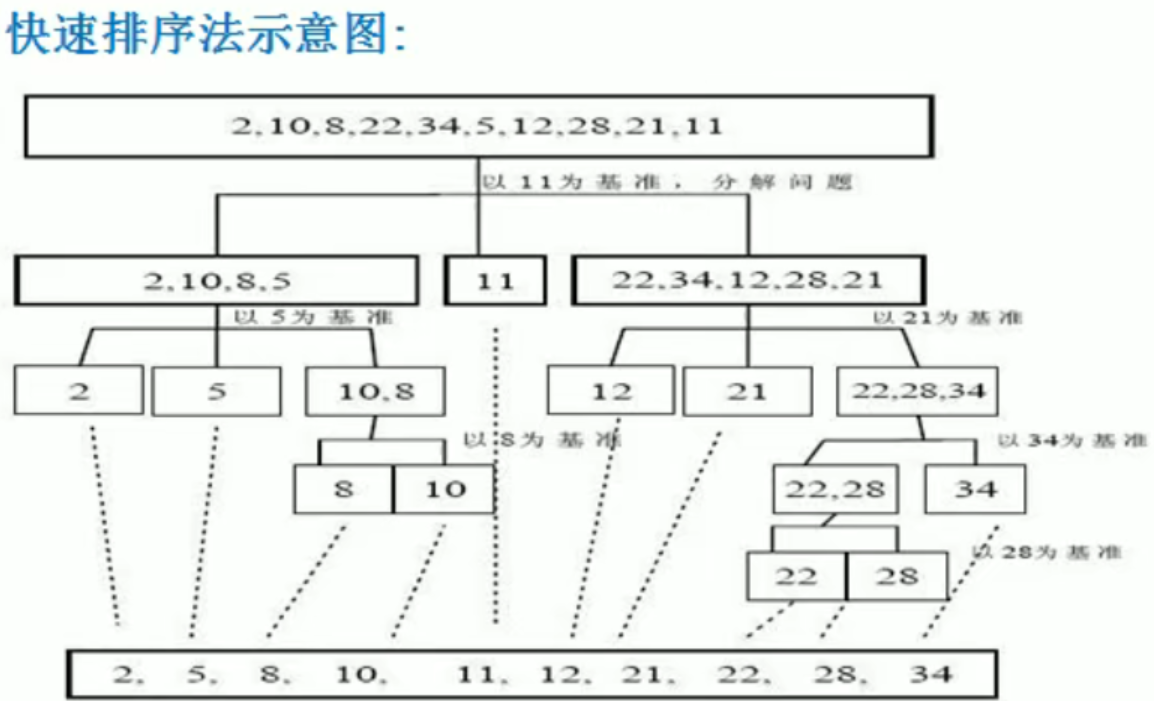Three steps of quick sort:
1) Select benchmark: in the sequence to be arranged, select an element in a certain way as the "pivot"
2) Segmentation operation: divide the sequence into two subsequences based on the actual position of the benchmark in the sequence. At this time, the elements on the left of the benchmark are smaller than the benchmark, and the elements on the right of the benchmark are larger than the benchmark
3) Two sequences are quickly sorted recursively until the sequence is empty or has only one element.
Optimization 1: optimize the selection of datum points
For the divide and conquer algorithm, if the algorithm can be divided into two equal length subsequences each time, the efficiency of the divide and conquer algorithm will reach the maximum. In other words, the choice of benchmark is very important. The way of selecting the benchmark determines the length of the two sub sequences after two segmentation, which has a decisive impact on the efficiency of the whole algorithm. The most ideal method is that the selected benchmark can just divide the sequence to be sorted into two equal length subsequences
Two methods of selecting datum
Method (1): fixed position
Idea: take the first or last element of the sequence as the benchmark
Note: the basic quick sort selects the first or last element as the benchmark. However, this has been a very bad way to deal with it.
Idea: take the middle element of the sequence as the benchmark.
Test data analysis: if the input sequence is random, the processing time is acceptable. If the array is already ordered, the segmentation at this time is a very bad segmentation. Because each partition can only reduce the sequence to be sorted by 1, this is the worst case, the quick sort becomes bubble sort, and the time complexity is O(n^2). Moreover, it is quite common that the input data is orderly or partially orderly. Therefore, using an element as a hub element is very bad. In order to avoid this situation, the following two methods for obtaining benchmarks are introduced.
Method (2): randomly select the benchmark
Reason for introduction: when the sequence to be arranged is partially ordered, the fixed selection pivot makes the fast arrangement efficiency lower. To alleviate this situation, the random selection pivot is introduced
Idea: take any element in the sequence to be arranged as the benchmark
int pivot = (int) (Math.random() * (r - l + 1)) + 1;
Test data analysis: This is a relatively safe strategy. Since the pivot position is random, the resulting segmentation will not always produce inferior segmentation. When the numbers of the whole array are all equal, it is still the worst case, and the time complexity is O(n^2). In fact, the probability of the theoretical worst case obtained by randomized quick sorting is only 1/(2^n). Therefore, randomized quick sorting can achieve the expected time complexity of O(nlogn) for most input data. An elder made a brilliant summary: "Randomized quick sorting can meet a person's personality needs for a lifetime."
Method (3): median of three
Analysis: the best division is to divide the sequence to be sorted into equal length subsequences. In the best state, we can use the middle value of the sequence, that is, the N/2 number. However, it is difficult to calculate and will significantly slow down the speed of rapid sorting. Such median estimation can be obtained by randomly selecting three elements and using their median as the hub element. In fact , randomness does not help much, so the general practice is to use the median of the three elements at the left, right and center as the hub element. Obviously, using the three number median segmentation method eliminates the bad situation of pre sorting input and reduces the comparison times of fast sorting by about 14%
For example, the sequence to be sorted is 8 1 4 9 6 3 5 2 7 0
8 on the left, 0 on the right and 6 in the middle
After we sort the three numbers here, the middle number is used as the pivot, and the pivot is 6
Note: when selecting the central axis value, you can expand the selection from the left, middle and right to five or more elements. Generally, there will be (2t + 1) average of - (2t + 1), and the three average of three in English.
Specific idea: sort the data at the three positions of low, mid and high in the sorting sequence, take the data in the middle as the pivot, and store the pivot with the 0 subscript element.
That is, three data fetches are used, and the 0 subscript element is used to store the pivot.
/**
* @return Take the data at the left, mid and right positions in the sequence to be sorted, and select the data in the middle as the pivot
*/
public static int SelectPivotMedianOfThree(int arr[], int left, int right) {
int temp = 0;
int mid = left + ((right - left) >> 1);// Evaluates the subscript of the element in the middle of the array
// Select the pivot using the triple center method
if (arr[mid] > arr[right]) {// Target: arr [mid] < = arr [right]
temp = arr[mid];
arr[mid] = arr[right];
arr[right] = temp;
}
if (arr[left] > arr[right]) {// Target: arr [left] < = arr [right]
temp = arr[left];
arr[left] = arr[right];
arr[right] = temp;
}
if (arr[mid] > arr[left]) {// Target: arr [left] < = arr [mid]
temp = arr[mid];
arr[mid] = arr[left];
arr[left] = temp;
}
// At this point, arr [mid] < = arr [left] < = arr [right]
// The left position retains the value with the middle size in these three positions
return arr[left];
}
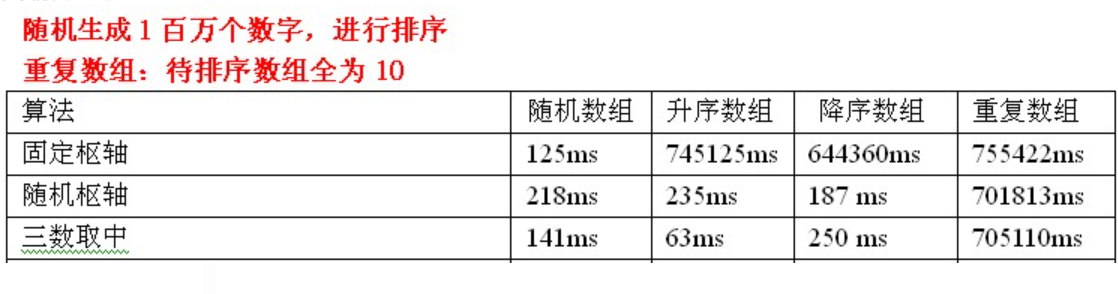
Test data analysis: the advantage of selecting pivot in three data retrieval is still obvious, but it still can't handle repeated arrays
Optimization 2: when the length of the sequence to be sorted is divided to a certain size, insert sorting is used
Reason: for small and partially ordered arrays, it is better to arrange them quickly than to arrange them. When the length of the sequence to be sorted is divided to a certain size, the following
The efficiency of continuous segmentation is worse than insertion sorting. At this time, you can use interpolation instead of fast sorting
Cut off range: the length of the sequence to be sorted is N = 10. Although any cut-off range between 5 and 20 may produce similar results, this
This approach also avoids some harmful degradation situations. Excerpted from data structure and algorithm analysis by Mark Allen Weiness
if (right - left + 1 < 10) {
insertSort(arr);
return;
}
//else normal quick sort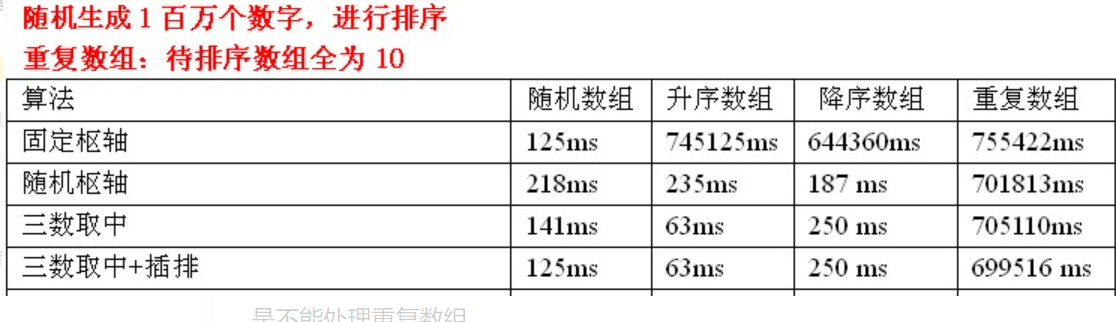
Test data analysis: for random arrays, the efficiency can be improved by selecting pivot + interpolation in three data extraction. It is really useless for sorted arrays. Because the sequence to be sorted is already ordered, each division can only reduce the sequence to be sorted by one. At this time, interpolation can not play a role. Therefore, there is no reduction in time. In addition, selecting pivot + interpolation in triple fetching still cannot process duplicate arrays
Optimization 3: three-way quick sorting (double principal component quick sorting)
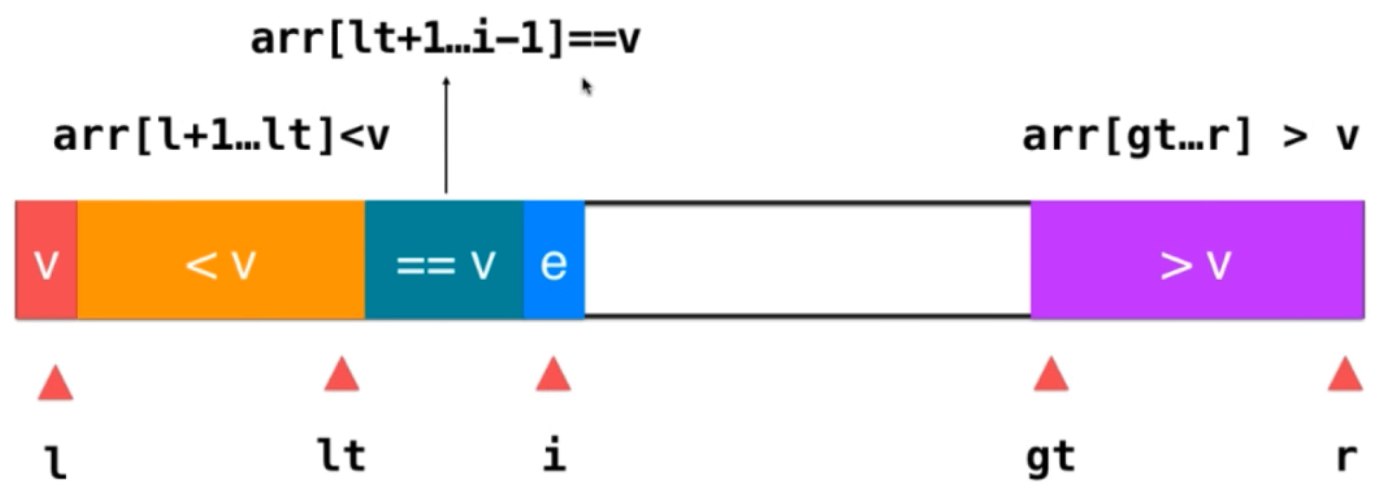
Divide the array into three parts: greater than v, less than v and equal to v; l represents the first element of less than v and r represents the last element of greater than v; therefore: arr[l + 1] ~~arr[lt] this part represents all elements less than v; arr[lt + 1]~~arr[i - 1] represents elements equal to v; arr[gt] ~~arr[r] It represents the elements greater than v; i represents the elements currently traversed; in this way, the data to be traversed is divided; the main problem now is, after dividing into such an interval, what should we do for a new element?
1) If e == v; integrate e into the element equal to v in the way of i + +;
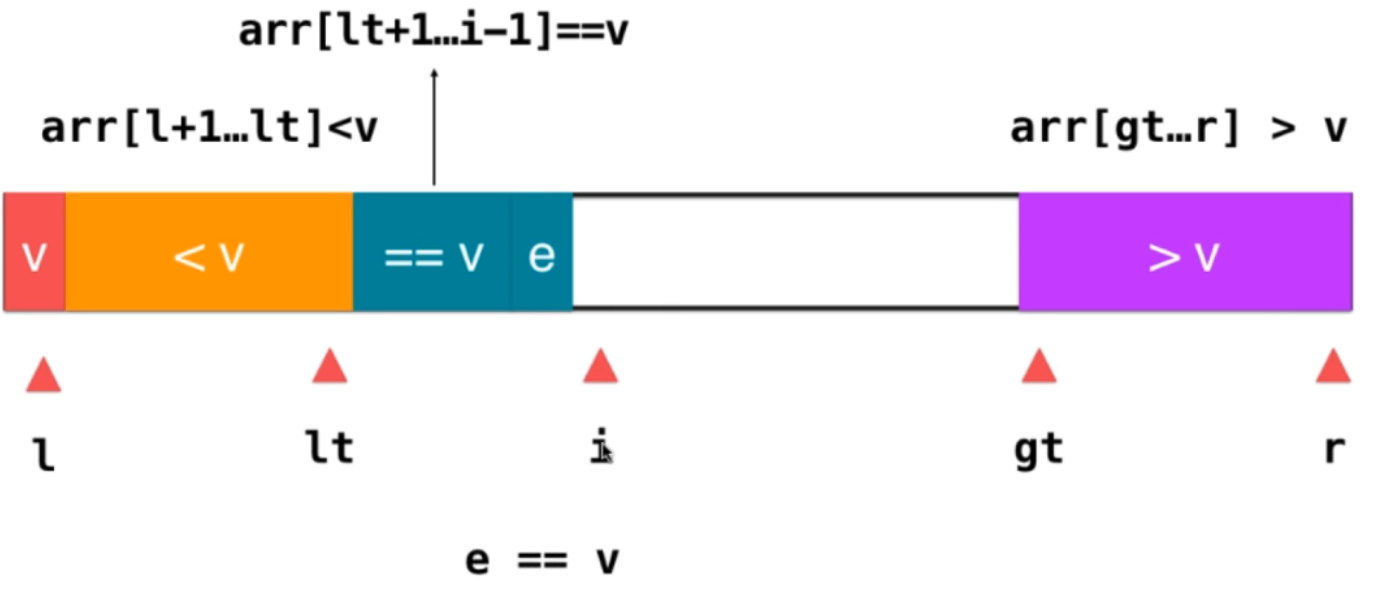
2) If it is e < v, you only need to exchange the position of E and the first element equal to v; after exchanging the position, e is located behind the part less than v; the meaning of this is to integrate e into the element less than v in the way of lt + +; then i + +, let's look at the next element
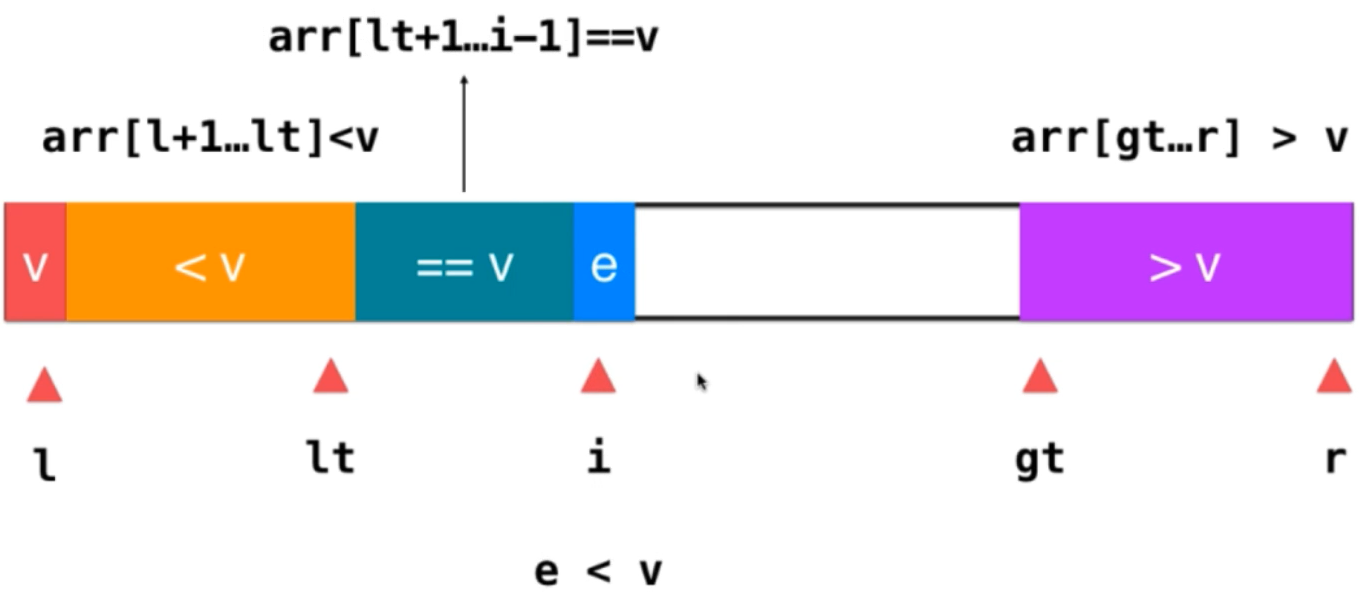
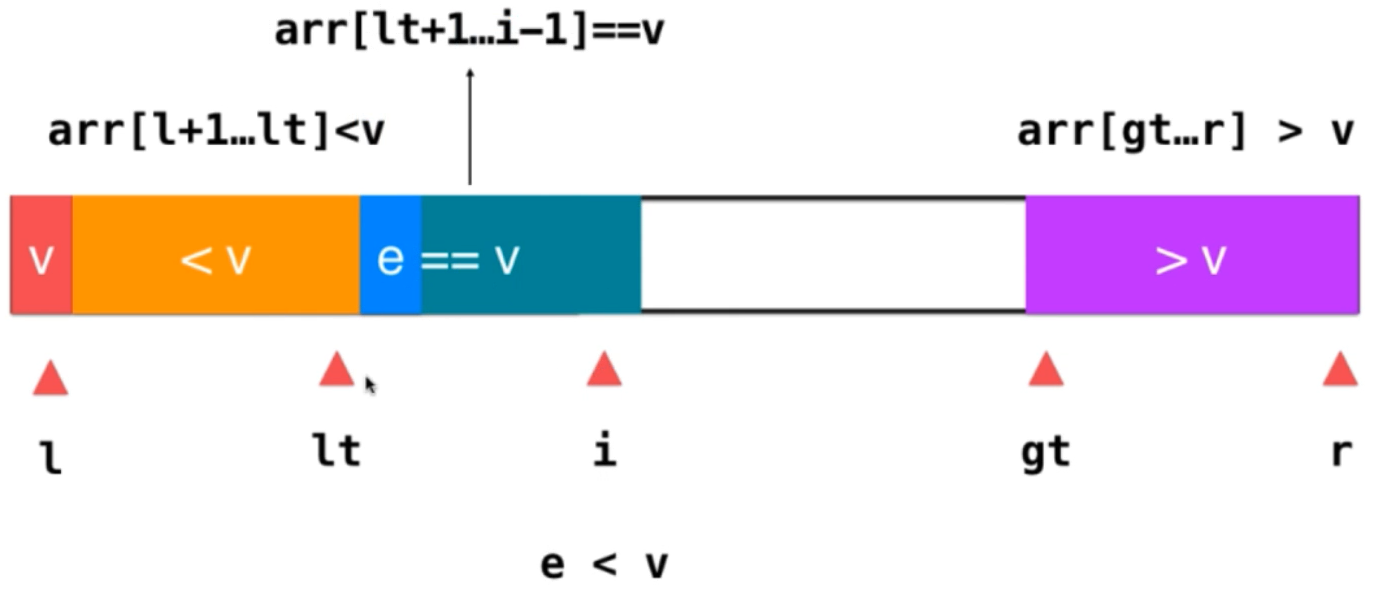
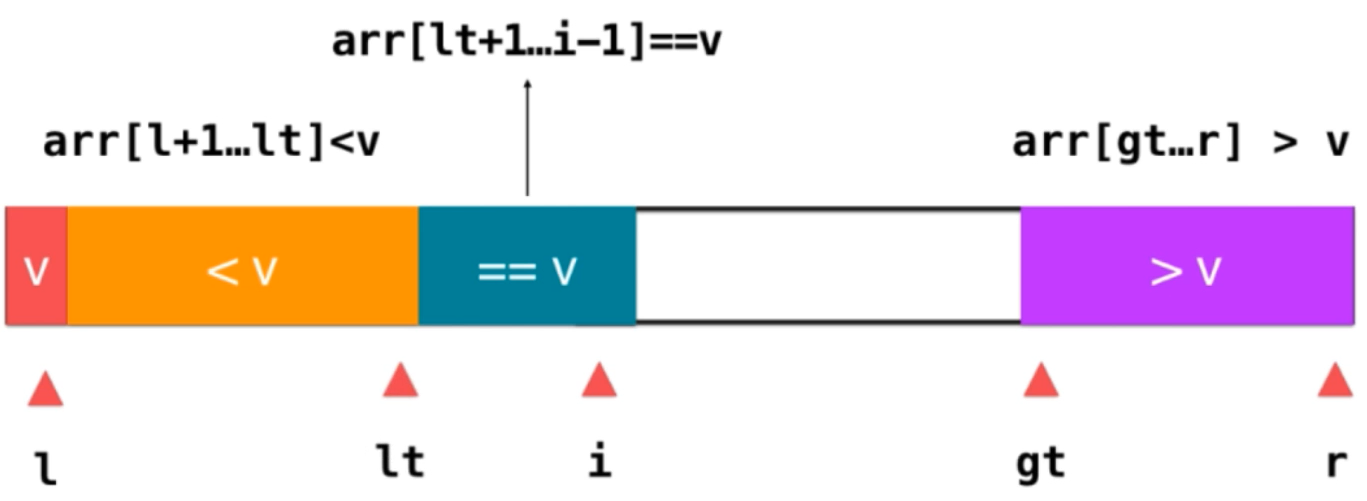
3) If e > V; you only need to exchange the position of this element with the previous element greater than v. at this time, the previous element of the original greater than V part is an element that has not been traversed. After exchange, put it in the position indicated by i, and E is already next to the element greater than v. at this time, integrate e into this part of the element. The operation is gt --; then i + +; because After the previous exchange, move an element not traversed to the position pointed to by i. at this time, just continue to judge this element
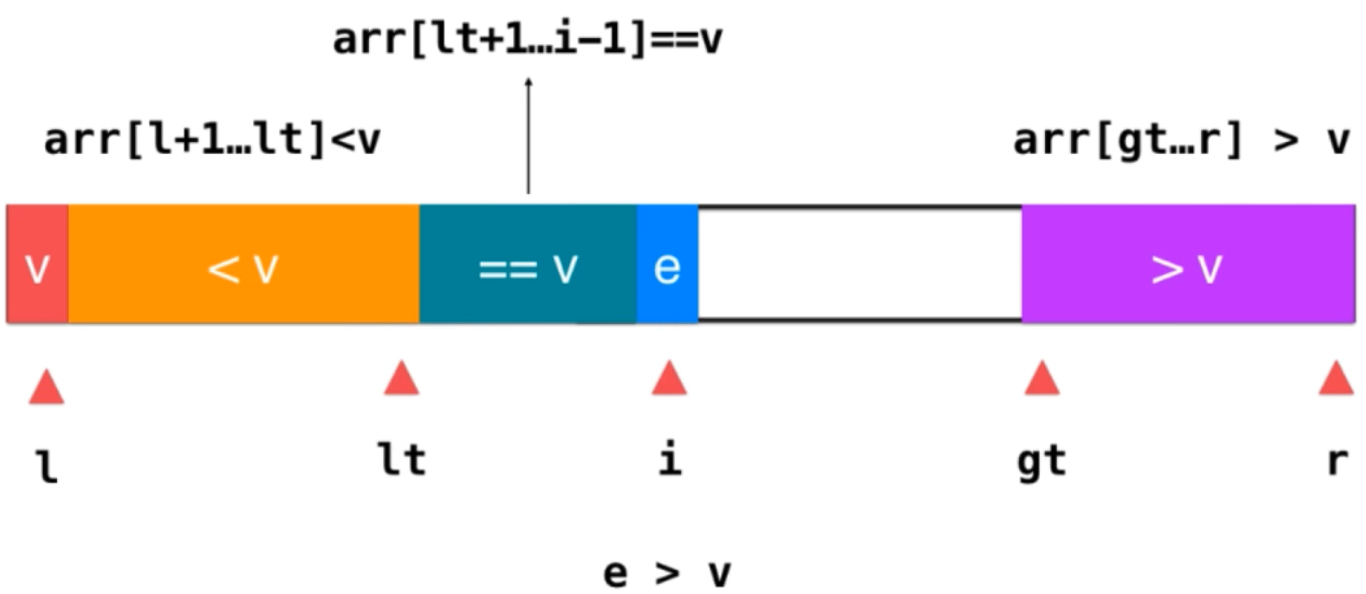
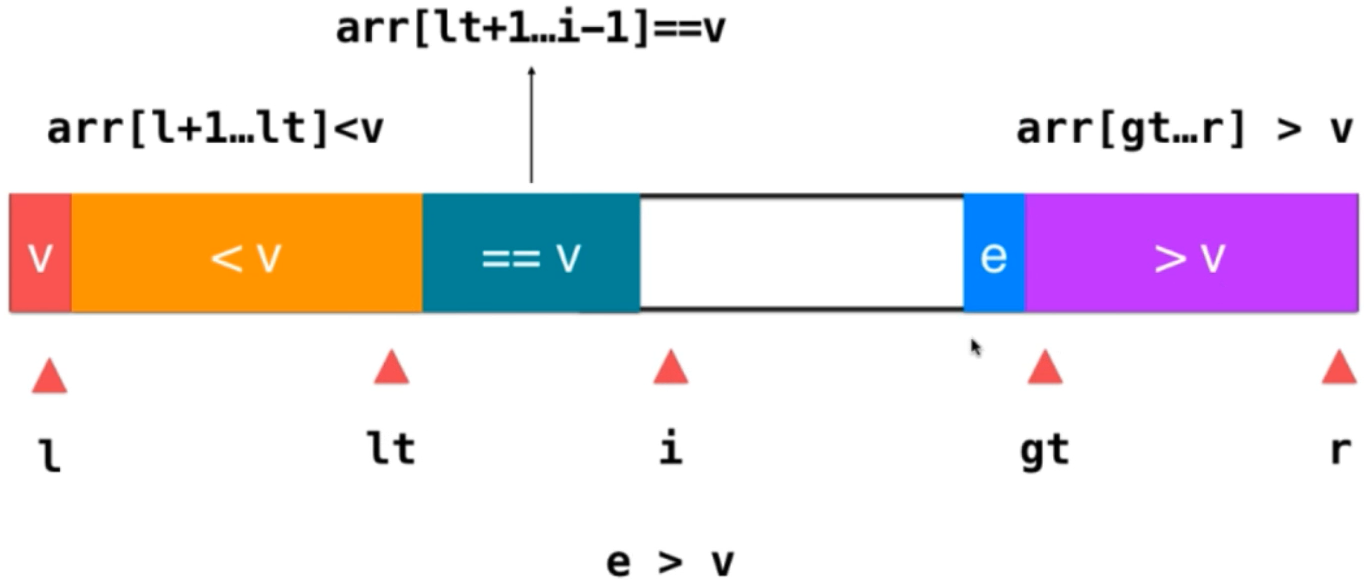
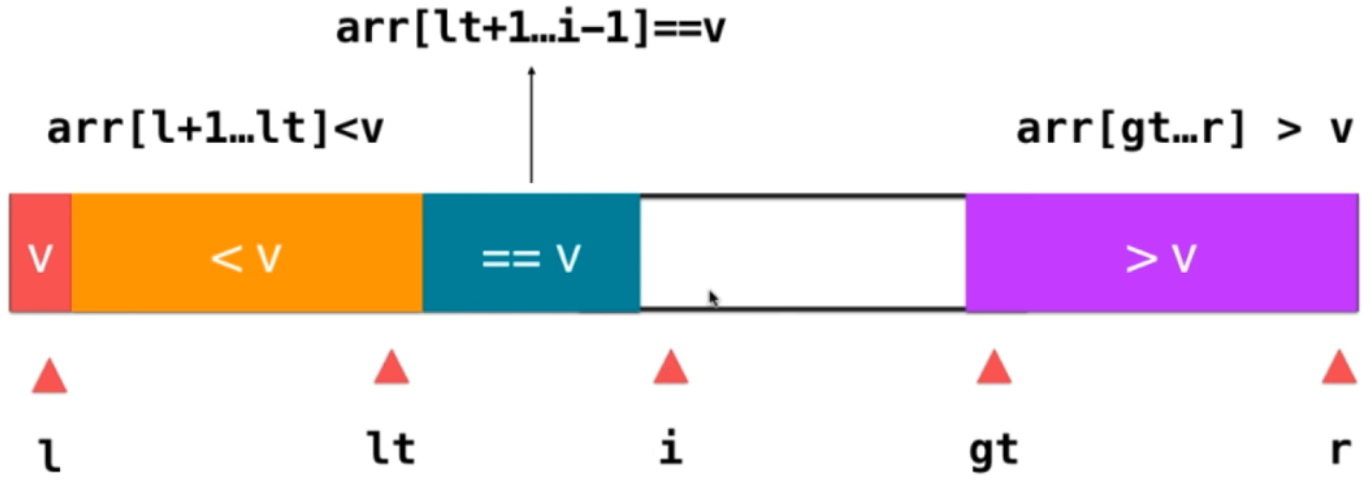
Finally, go on using the above method, and the original data is divided into three parts. The termination condition is i == gt, which means that all elements have been traversed. Then, exchange the position between the element V and the element pointed to by lt, so that the elements on the left of lt are elements less than V, and the elements on the right are elements greater than or equal to V; V and elements equal to v If the elements are integrated, you don't need to consider the elements equal to V; next, you only need to recursively sort the elements greater than V and less than V; the advantages of three-way sorting: you don't need to consider duplicate elements. In extreme cases, if all the data elements to be sorted are equal, you only need a round of three-way fast sorting to arrange all the elements in order The time complexity evolves to O (n). Three-way fast scheduling can handle data with a large number of repeated elements very well, and also has a good effect on almost ordered data and completely disordered data. It is the underlying implementation of sorting algorithms in many language standard libraries. Java is like this
public static void quickSort5(int[] arr, int left, int right) {
int l = left;// Left subscript
int r = right;// Right subscript
// Define axis values
// int pivot = arr[(left + right) / 2];
int pivot = (int) (Math.random() * (r - l + 1)) + l;
int temp = 0;
int v = arr[l];
temp = arr[l];
arr[l] = pivot;
pivot = temp;
int lt = l;
int gt = r + 1;
int i = l + 1;
while (i < gt) {
if (arr[i] < v) {
temp = arr[i];
arr[i] = arr[lt + 1];
arr[lt + 1] = temp;
lt++;
i++;
} else if (arr[i] > v) {
temp = arr[i];
arr[i] = arr[gt - 1];
arr[gt - 1] = temp;
gt--;
} else {
i++;
}
}
// exchange
temp = arr[l];
arr[l] = arr[lt];
arr[lt] = temp;
quickSort5(arr, l, lt - 1);
quickSort5(arr, gt, r);
}
Optimization 4: tail recursive sorting
The fast sorting function has two recursive operations at the end of the function. We can use tail recursive optimization for it
Advantages: if the sequence to be sorted is extremely unbalanced, the depth of recursion will approach n, and the size of the stack is very limited. Each recursive call will consume a certain stack space. The more parameters of the function, the more space each recursion will consume. After optimization, the stack depth can be reduced from O(n) to O(logn), which will improve performance.
Conclusion: tail recursion is characterized by no operation in the regression process. This feature is very important because most current compilers will use this feature to automatically generate optimized code; So I think it's good for programmers to know this way of tail recursion, because in practice, whether your code has tail recursion or not, the compiler will optimize your code, so there is no specific code. Focus on the three-way fast row above!!
Practical application of quick sort
The bottom layer of the sorting algorithm in Java 7 uses three-way fast scheduling. The bottom layer of the sorting algorithm in Go integrates the comprehensive version of insertion sorting, three-bit selection benchmark and three-way fast scheduling. Insert sorting and Hill sorting are used for small data. Heap sorting is also used to avoid stack overflow of large data. Generally, Go will give priority to three-way fast sorting.