catalogue
Time complexity is an indicator of estimating constant operations
Constant operation
What has nothing to do with the amount of data is a fixed time thing, and what is related to the amount of data is not a constant operation
For example, the addressing of an array has nothing to do with the amount of data. We just want to find the number of i positions
Addition, subtraction, multiplication, division and bit operations are constant operations
For a linked list, this is not a constant operation. For a single linked list, you can only find it one by one from left to right

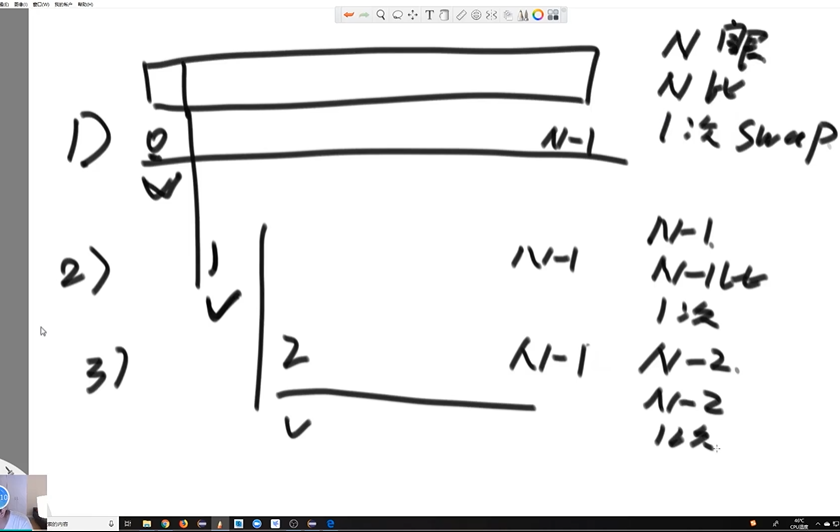
Select sort
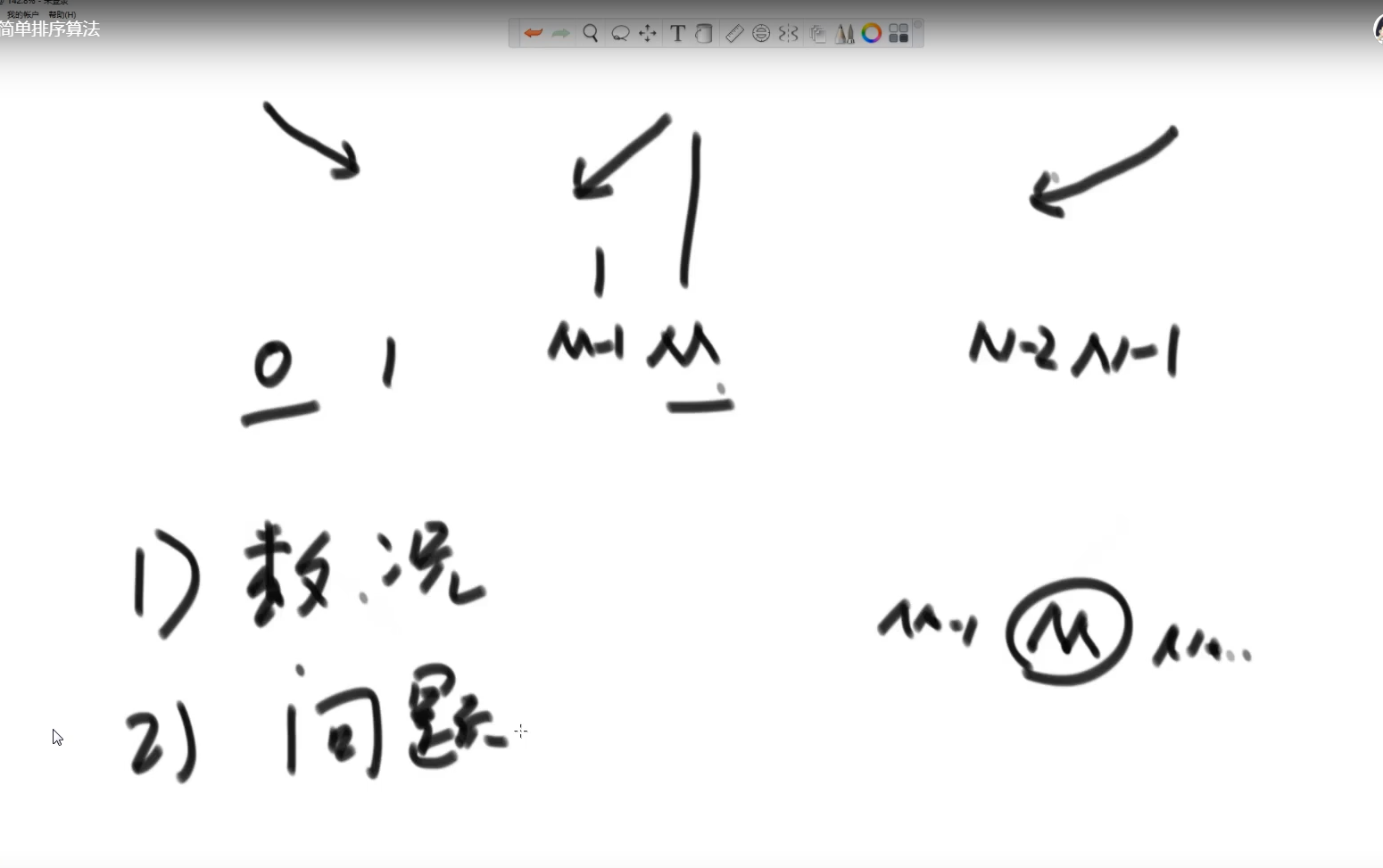
Traverse to find the minimum value, record it, and exchange it with the value at position (0)
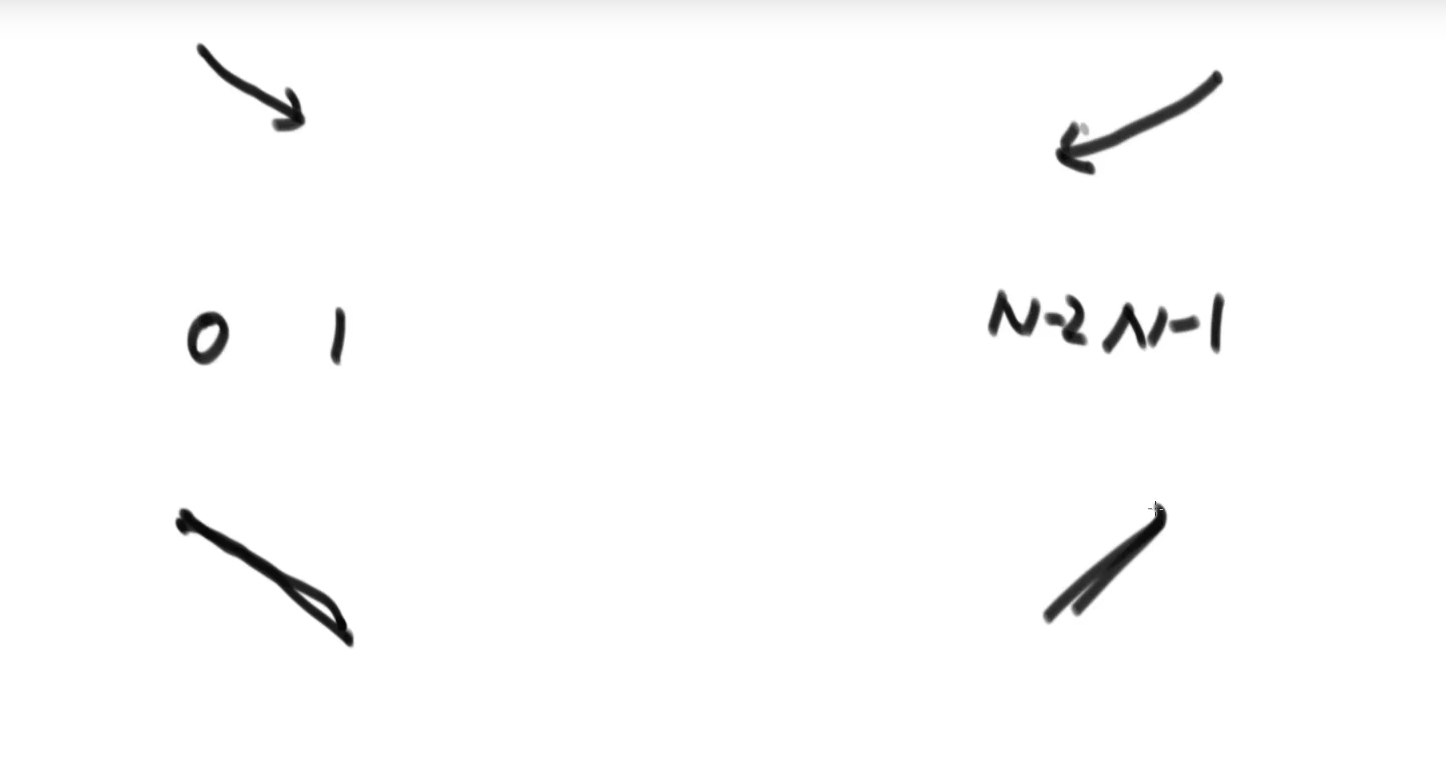
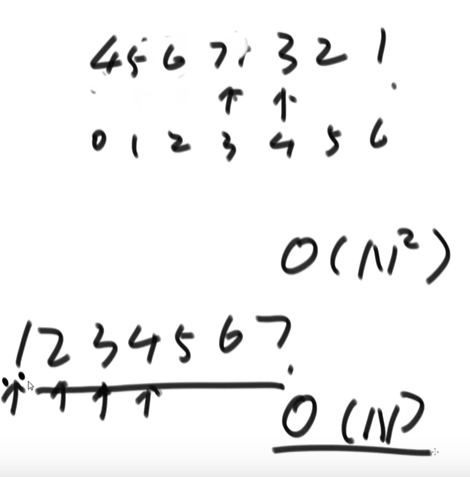
The first time: take a look at the n elements in the array. Each number you see should be compared with the minimum value found before. Until the minimum value is found after reading, it should be placed at the position with index 0. You need to look at n eyes, compare n-1 times and exchange once
The second time: take a look at the N-1 elements in the array. Each number you see should be compared with the minimum value found before. You know that the minimum value is found and placed at the position with index 1. You need to take a look at n-1, compare n-2 times and exchange once
The final range will be compressed
Find the smallest number, the smaller number, the smaller number, and so on. In this way, the array will be arranged in good order, which is very inefficient

O(n)
Take n as the upper limit
Small amount of data
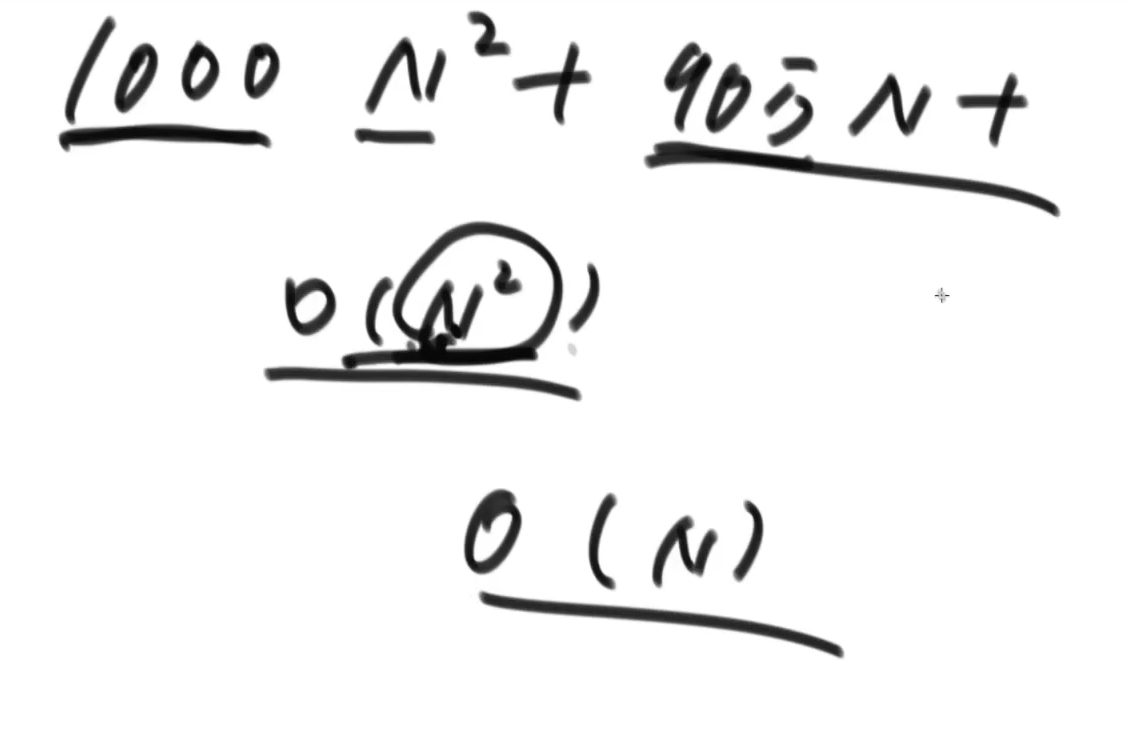
code
public class Code01_SelectionSort {
public static void selectionSort(int[] arr) {
if (arr == null || arr.length < 2) {//Eliminate troublemakers
return;
}
for (int i = 0; i < arr.length-1; i++) {//i~n-1
int minIndex=i;
for(int j=i+1;j<arr.length;j++){//Find the minimum subscript on i~n-1
minIndex=arr[j]<arr[minIndex]?j:minIndex;
}
swap(arr,i,minIndex);
}
}
public static void swap(int[] arr ,int i,int j){
int temp=arr[i];
arr[i]=arr[j];
arr[j]=temp;
}
}XOR operation

XOR operation is to observe whether a number in binary bits is odd or even
Odd number is 1 and even number is 0
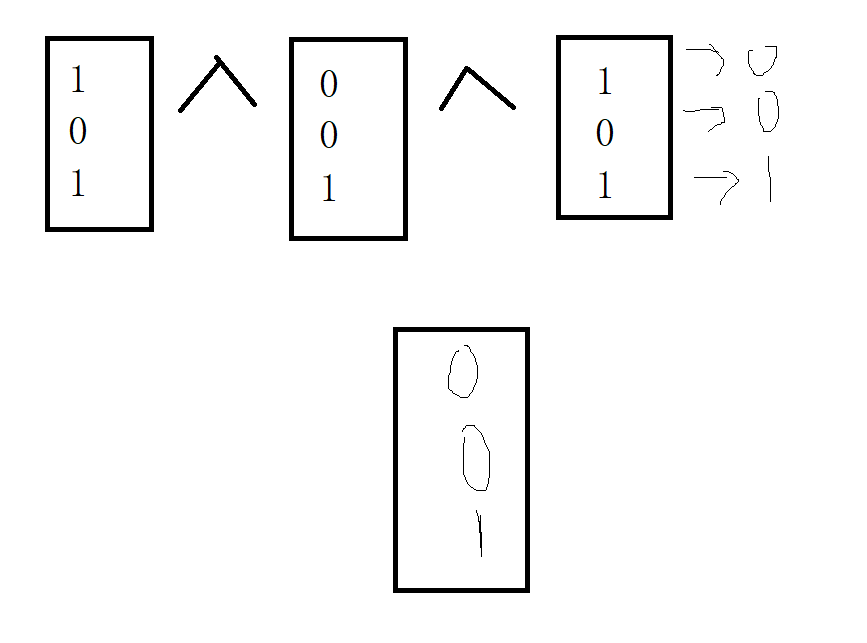
XOR operation can be understood as addition without carry, and bit is binary bit
XOR operation satisfies commutative law and associative law, so for XOR operation, the order of logarithmic XOR is irrelevant, and only one number will be obtained
For example, in an array The element of is 8 7 3 6 3 6 7 8 2 1 1 2 3. Let a 0 XOR all the elements in this array. The final result is 3 Because the elements in the array can be regarded as 1 1 2 2 3 3 6 7 8 8, of which the number of odd times is only 3, and the rest will become 0 in XOR

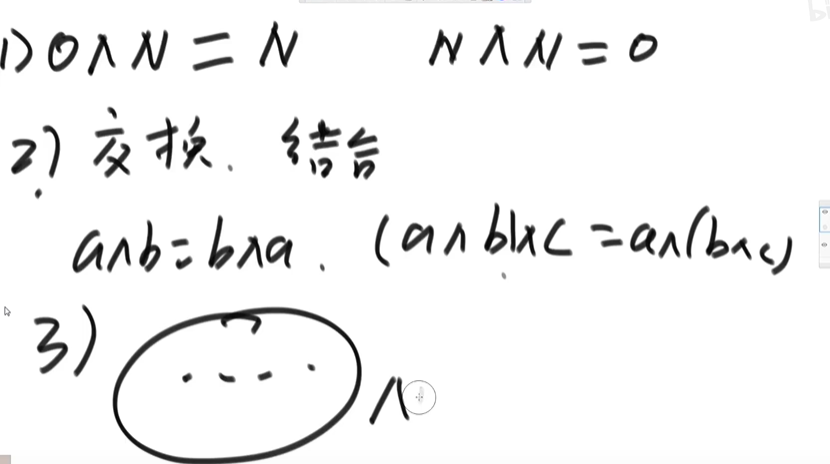
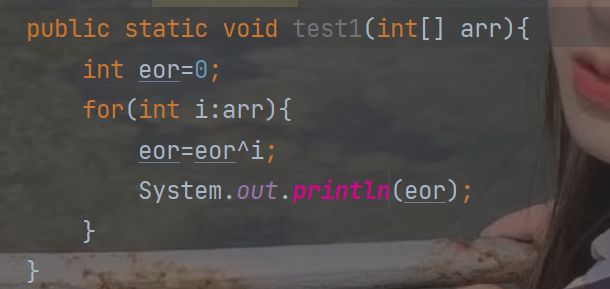
Title: one number in an array appears odd times, and the others appear even times. Find the number that appears odd times
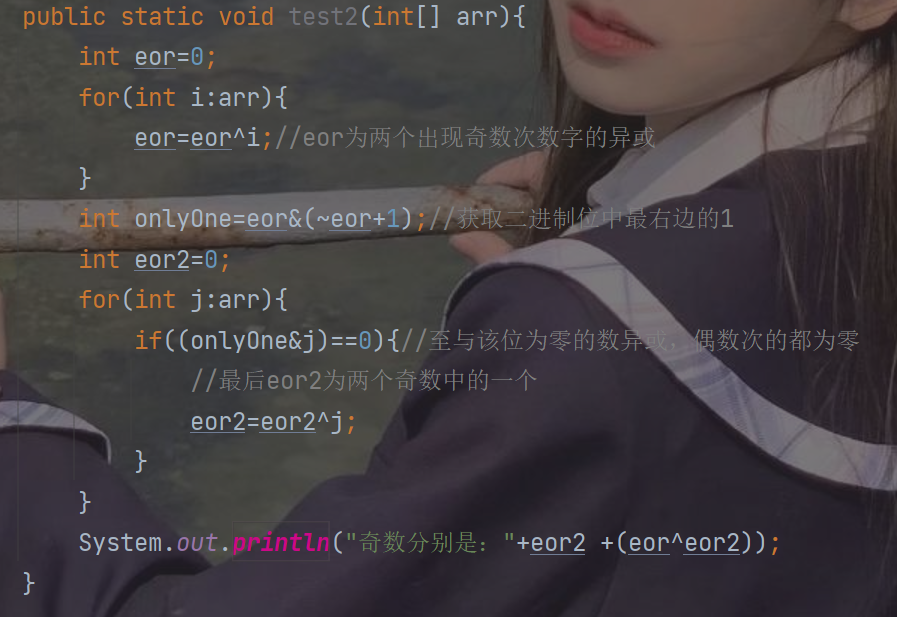
Title: two numbers in an array appear odd times, and the rest appear even times. Find out the two numbers that appear odd times
Insert sort (On^2)
The time complexity of the algorithm is always estimated according to the worst time
Insert sort is 0 ~ 0, 0 ~ 1, 0 ~ 2, 0 ~ 3 ..... The numbers in the range of 0~n are orderly, which is related to the data status. For example, selective sorting is to find the smallest number at 0~n,1~n,2~n... And put it at 0,1,2...n. It has nothing to do with the data volume (the status of the original data cannot affect the process), and bubble sorting has nothing to do with the data volume
Insertion sorting is related to the amount of data. We make the numbers at 0-i in order, while the numbers at 0~i-1 are already in order, so we just need to judge the position of the elements at i

ublic class Code04_InsertionSort {
public static void InsertionSort(int[] arr){
if(arr==null || arr.length<2) {
return;
}
//The numbers at 0 ~ 0 are in order
//Order the numbers at 0~i
for(int i=1;i<arr.length;i++){//[1-n), order the numbers from 1 to n-1
for(int j=i-1;j>=0&&arr[j]>arr[j+1];j--){//0 -- the numbers at i-1 are in order
swap(arr,j,j+1);
}
}
}
public static void swap(int[] arr,int i,int j){
arr[i]=arr[i]^arr[j];
arr[j]=arr[i]^arr[j];
arr[i]=arr[i]^arr[j];
}
} The algorithm flow is estimated according to the worst time complexity. The insertion sort has a good time complexity of O(n), that is, if they are all ordered, they will have a look, while the worst is that O (n^2) is disordered
Binary search
package com;
public class Code05_Search {
public static boolean search(int[] sortArr,int num){
if(sortArr==null||sortArr.length==0){
return false;
}
int l=0;
int r=sortArr.length-1;
while(l<r){
int mid=l+((l-r)>>1);
if(sortArr[mid]==num){
return true;
}else if(sortArr[mid]>num){
r=mid-1;
}else{
l=mid+1;
}
}
return sortArr[l]==num;//Finally, r and l point to the same number
}
}

Binary search is mostly used to check whether a number exists in an ordered array, or to find the position greater than or equal to the rightmost number of a number, or the position less than or equal to the rightmost number of a number, or the local minimum. The time complexity is O(lg2n)n is the number of elements in the array. Assuming that there are 16 elements in the array, the best case is to find them in the first bisection. At this time, the complexity is O(1), and the worst case is that they are bisected four times. The time complexity is O(4)
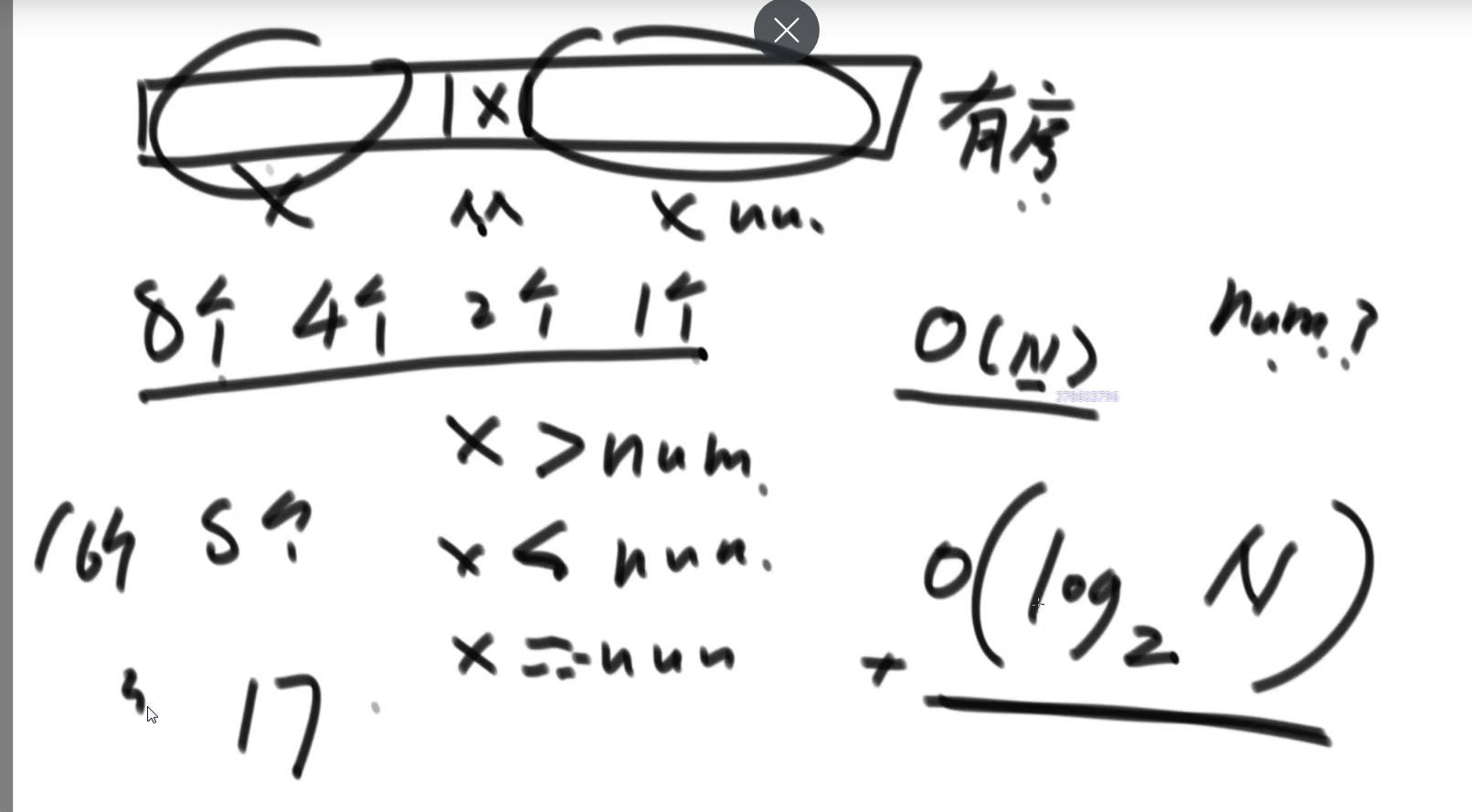
Suppose the number to be found is set to num. when the middle element x > num, because the array is ordered, the numbers on the right of X are greater than num, so we can cut half and continue to score two points on the left of X. if x2 < num, because the array is ordered, the numbers on the left of x1 will be less than num, and we can cut off the left of x1 every time Two points will reduce the search scope by half
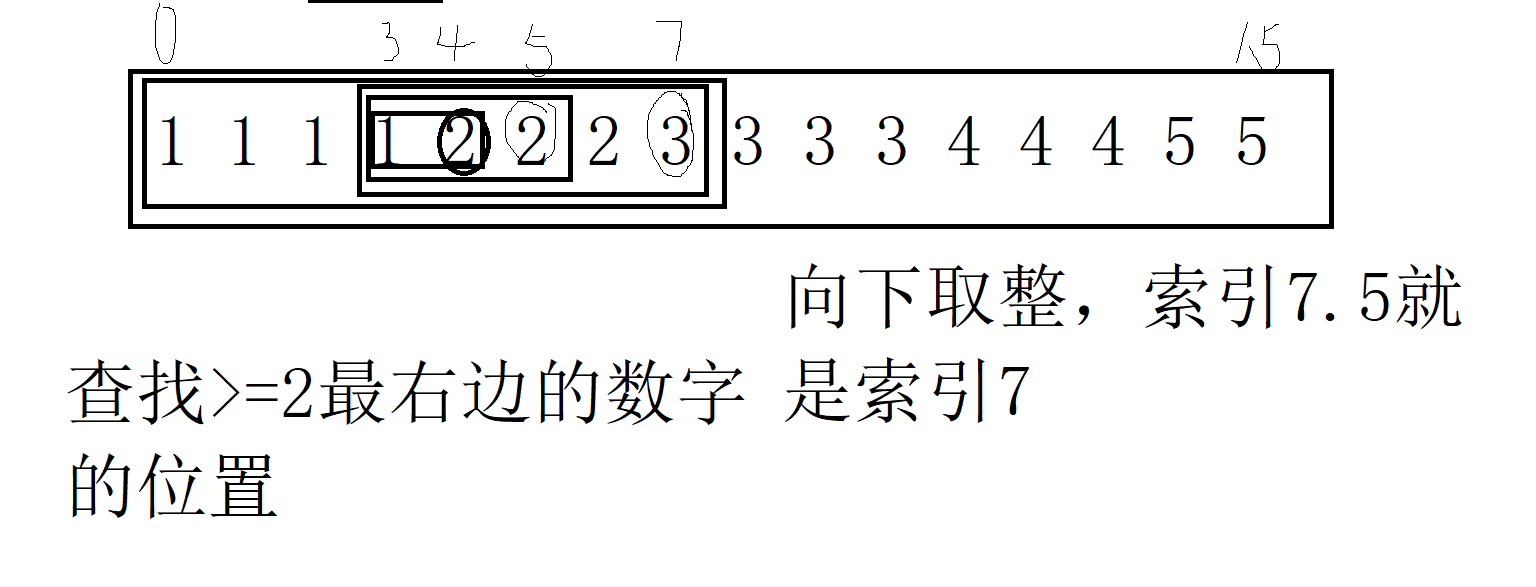
Binary lookup can also be used for unordered
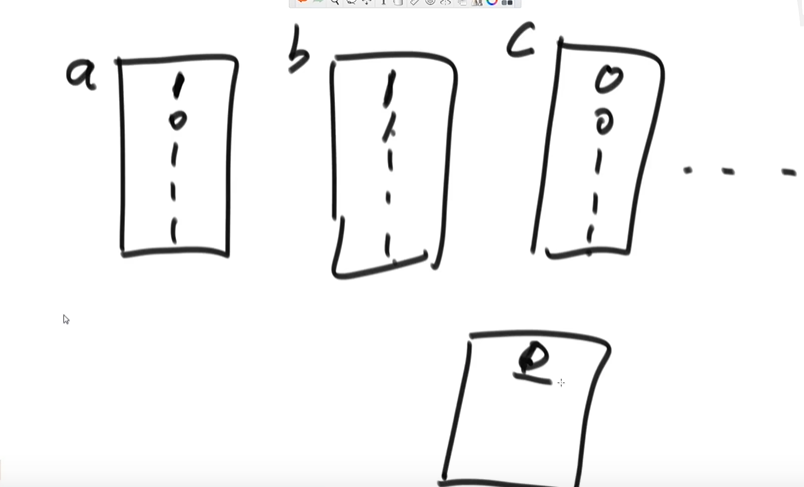
Local minimum problem
If two adjacent numbers are not equal, there must be a fluctuation curve of values in the whole array
Then there must be a local minimum at 0-n-1