FCM algorithm is a clustering algorithm based on partition. Its idea is to maximize the similarity between objects divided into the same cluster and minimize the similarity between different clusters. Fuzzy C-means algorithm is an improvement of ordinary C-means algorithm. Ordinary C-means algorithm is hard for data division, while FCM is a flexible fuzzy division. Before introducing the specific algorithm of FCM, we first introduce some basic knowledge of fuzzy sets.
one Basic knowledge of fuzzy sets
Firstly, the concept of membership function is explained. Membership function is a function indicating the degree to which an object x belongs to set a, which is usually recorded as μ A (x), whose argument range is all objects that may belong to set a (i.e. all points in the space where set a is located), and the value range is [0,1], i.e. 0<= μ A(x)<=1. μ A(x)=1 means that x completely belongs to set a, which is equivalent to X ∈ a in the traditional set concept. A membership function defined on space X={x} defines a fuzzy set a, or a fuzzy subset defined on universe X={x}. For a finite number of objects x1, x2,..., xn fuzzy sets can be expressed as:
(6.1)
With the concept of fuzzy set, it is not hard for an element to belong to fuzzy set. In the problem of clustering, the cluster generated by clustering can be regarded as fuzzy set. Therefore, the membership degree of each sample point belonging to the cluster is the value in the [0,1] interval.
two Introduction to K-means clustering algorithm (HCM, K-Means)
K-Means clustering, known as c-means clustering, has been applied to various fields. Its core idea is as follows: the algorithm divides n vectors xj(1,2,..., n) into C groups Gi(i=1,2,..., c), and finds the cluster center of each group to minimize the value function (or objective function) of the dissimilarity (or distance) index. When the Euclidean distance is selected as the dissimilarity index between the vector xk in group j and the corresponding cluster center ci, the value function can be defined as:
(6.2)
Here is the value function within group i. In this way, the value of Ji depends on the geometric characteristics of Gi and the position of ci.
Generally speaking, a general distance function d(xk,ci) can be used to replace the vector xk in group I, and the corresponding total value function can be expressed as:
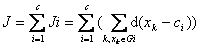(6.3)
For simplicity, the Euclidean distance is used as the dissimilarity index of the vector, and the total value function is expressed as equation (6.2).
Divided groups usually use a c × n is defined by the two-dimensional membership matrix U. If the j-th data point xj belongs to group i, the element uij in U is 1; Otherwise, the element takes 0. Once the cluster center ci is determined, the following equation (6.2) can be derived to minimize uij:
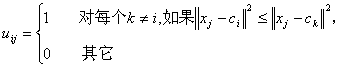(6.4)
Again, if ci is the nearest cluster center of xj, xj belongs to group i. Since a given data can only belong to one group, the membership matrix U has the following properties:
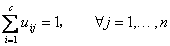(6.5)
And
(6.6)
On the other hand, if uij is fixed, the best clustering center that minimizes equation (6.2) is the mean value of all vectors in group I:
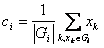(6.7)
Here | Gi | is the size or of Gi.
In order to run in batch mode, the K-means algorithm of data set xi (1, 2..., n) is given here; The algorithm repeats the following steps to determine the cluster center ci and the membership matrix U:
Step 1: initialize the cluster center ci,i=1,..., c. A typical approach is to take any c points from all data points.
Step 2: determine the membership matrix U with equation (6.4).
Step 3: calculate the value function according to equation (6.2). If it is less than a certain threshold, or its qualitative change relative to the last value function is less than a certain threshold, the algorithm stops.
Step 4: correct the cluster center according to equation (6.5). Return to step 2.
The algorithm itself is iterative and can not ensure that it converges to the optimal solution. The performance of K-means algorithm depends on the initial position of cluster center. Therefore, in order to make it desirable, either use some front-end methods to find the good initial clustering center; Or run the algorithm multiple times with different initial clustering centers each time. In addition, the above algorithm is only a representative method; We can also initialize an arbitrary membership matrix first, and then perform the iterative process.
The K-means algorithm can also run online. At this time, the corresponding cluster center and corresponding group are derived through time average. That is, for a given data point x, the algorithm calculates the nearest cluster center ci and modifies it with the following formula:
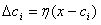(6.8)
This online formula essentially embeds many learning rules of unsupervised learning neural networks.
three Fuzzy C-means clustering
Fuzzy C-means clustering (FCM), known as fuzzy ISODATA, is a clustering algorithm that uses membership to determine the degree to which each data point belongs to a cluster. In 1973, Bezdek proposed the algorithm as an improvement of the early hard C-means clustering (HCM) method.
FCM divides n vectors xi (i=1,2,..., n) into c fuzzy groups, and calculates the clustering center of each group to minimize the value function of dissimilarity index. The main difference between FCM and HCM is that FCM uses fuzzy division, so that each given data point uses the membership degree between 0 and 1 to determine its degree of belonging to each group. According to the introduction of fuzzy partition, the membership matrix U allows elements with values between 0 and 1. However, in addition to the normalization provisions, the sum of the membership degrees of a data set is always equal to 1:
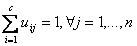(6.9)
Then, the value function (or objective function) of FCM is the generalized form of equation (6.2):
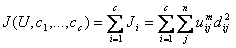(6.10)
Here uij is between 0 and 1; Ci is the cluster center of fuzzy group I, DIJ = ||ci xj|is the Euclidean distance between the i-th cluster center and the j-th data point; And is a weighted index.
The following new objective function is constructed to obtain the necessary conditions for minimizing equation (6.10):
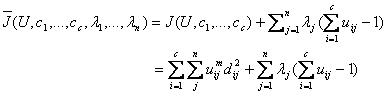(6.11)
Here lj, j=1 to n, is the Lagrange multiplier of n constraints of equation (6.9). The necessary conditions for deriving all input parameters to minimize equation (6.10) are:
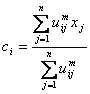(6.12)
and
(6.13)
According to the above two necessary conditions, the fuzzy C-means clustering algorithm is a simple iterative process. When running in batch mode, FCM uses the following steps to determine the cluster center ci and the membership matrix U[1]:
Step 1: initialize the membership matrix U with a random number between 0 and 1 to meet the constraints in equation (6.9)
Step 2: calculate c cluster centers ci, i=1,..., c with equation (6.12).
Step 3: calculate the value function according to equation (6.10). If it is less than a certain threshold, or its change from the last value function value is less than a certain threshold, the algorithm stops.
Step 4: calculate the new U matrix with (6.13). Return to step 2.
The above algorithm can also initialize the cluster center first, and then execute the iterative process. Because FCM can not be guaranteed to converge to an optimal solution. The performance of the algorithm depends on the initial clustering center. Therefore, we either use another fast algorithm to determine the initial clustering center, or start the algorithm with different initial clustering centers each time and run FCM many times.
four Application of FCM algorithm
From the above discussion, it is not difficult to see that FCM algorithm requires two parameters, one is the number of clusters C, and the other is the parameter M. Generally speaking, C should be far less than the total number of cluster samples, and C > 1 should be ensured. For m, it is a parameter that controls the flexibility of the algorithm. If M is too large, the clustering effect will be very poor, and if M is too small, the algorithm will be close to HCM clustering algorithm.
The output of the algorithm is C clustering center point vectors and a fuzzy partition matrix of C*N. this matrix represents the membership degree of each sample point belonging to each class. According to this partition matrix, according to the maximum membership principle in the fuzzy set, we can determine which class each sample point belongs to. The cluster center represents the average characteristics of each class and can be considered as the representative point of this class.
function varargout = CT_image_FCM(varargin)
% CT_IMAGE_FCM MATLAB code for CT_image_FCM.fig
% CT_IMAGE_FCM, by itself, creates a new CT_IMAGE_FCM or raises the existing
% singleton*.
%
% H = CT_IMAGE_FCM returns the handle to a new CT_IMAGE_FCM or the handle to
% the existing singleton*.
%
% CT_IMAGE_FCM('CALLBACK',hObject,eventData,handles,...) calls the local
% function named CALLBACK in CT_IMAGE_FCM.M with the given input arguments.
%
% CT_IMAGE_FCM('Property','Value',...) creates a new CT_IMAGE_FCM or raises the
% existing singleton*. Starting from the left, property value pairs are
% applied to the GUI before CT_image_FCM_OpeningFcn gets called. An
% unrecognized property name or invalid value makes property application
% stop. All inputs are passed to CT_image_FCM_OpeningFcn via varargin.
%
% *See GUI Options on GUIDE's Tools menu. Choose "GUI allows only one
% instance to run (singleton)".
%
% See also: GUIDE, GUIDATA, GUIHANDLES
% Edit the above text to modify the response to help CT_image_FCM
% Last Modified by GUIDE v2.5 17-Apr-2020 00:06:23
% Begin initialization code - DO NOT EDIT
gui_Singleton = 1;
gui_State = struct('gui_Name', mfilename, ...
'gui_Singleton', gui_Singleton, ...
'gui_OpeningFcn', @CT_image_FCM_OpeningFcn, ...
'gui_OutputFcn', @CT_image_FCM_OutputFcn, ...
'gui_LayoutFcn', [] , ...
'gui_Callback', []);
if nargin && ischar(varargin{1})
gui_State.gui_Callback = str2func(varargin{1});
end
if nargout
[varargout{1:nargout}] = gui_mainfcn(gui_State, varargin{:});
else
gui_mainfcn(gui_State, varargin{:});
end
% End initialization code - DO NOT EDIT
% --- Executes just before CT_image_FCM is made visible.
function CT_image_FCM_OpeningFcn(hObject, eventdata, handles, varargin)
% This function has no output args, see OutputFcn.
% hObject handle to figure
% eventdata reserved - to be defined in a future version of MATLAB
% handles structure with handles and user data (see GUIDATA)
% varargin command line arguments to CT_image_FCM (see VARARGIN)
% Choose default command line output for CT_image_FCM
handles.output = hObject;
% Update handles structure
guidata(hObject, handles);
% UIWAIT makes CT_image_FCM wait for user response (see UIRESUME)
% uiwait(handles.figure1);
% --- Outputs from this function are returned to the command line.
function varargout = CT_image_FCM_OutputFcn(hObject, eventdata, handles)
% varargout cell array for returning output args (see VARARGOUT);
% hObject handle to figure
% eventdata reserved - to be defined in a future version of MATLAB
% handles structure with handles and user data (see GUIDATA)
% Get default command line output from handles structure
varargout{1} = handles.output;
% --- Executes on button press in pushbutton1.
function pushbutton1_Callback(hObject, eventdata, handles)
% hObject handle to pushbutton1 (see GCBO)
% eventdata reserved - to be defined in a future version of MATLAB
% handles structure with handles and user data (see GUIDATA)
global I
[filename, pathname]= ...
uigetfile({'*.*';'*.bmp';'*.tif';'*.png';'*.jpg'},'select picture');
str= [pathname filename];
I= imread(str);
axes(handles.axes1);
imshow(I);
title('Original drawing');
% --- Executes on button press in pushbutton2.
function pushbutton2_Callback(hObject, eventdata, handles)
% hObject handle to pushbutton2 (see GCBO)
% eventdata reserved - to be defined in a future version of MATLAB
% handles structure with handles and user data (see GUIDATA)
% --- Executes on button press in pushbutton3.
function pushbutton3_Callback(hObject, eventdata, handles)
% hObject handle to pushbutton3 (see GCBO)
% eventdata reserved - to be defined in a future version of MATLAB
% handles structure with handles and user data (see GUIDATA)
global I I0 A
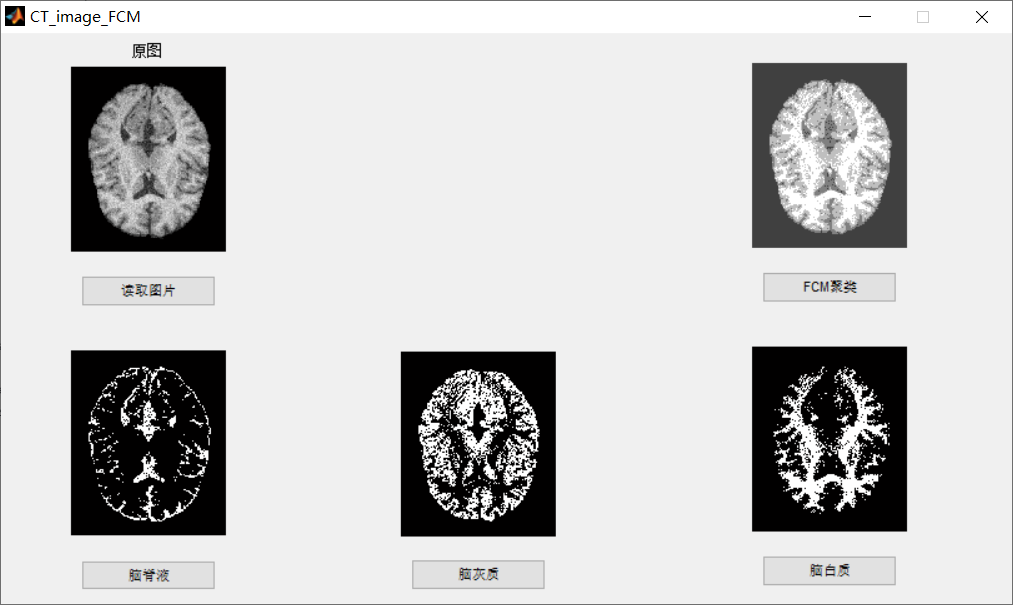
[I2,clusterResult] = FCM1(I, 4,[0 80 160 255],2,150,1e-5);
axes(handles.axes3);
imshow(I2)
I0=I2;
A=unique(I0);
% --- Executes on button press in pushbutton4.
function pushbutton4_Callback(hObject, eventdata, handles)
% hObject handle to pushbutton4 (see GCBO)
% eventdata reserved - to be defined in a future version of MATLAB
% handles structure with handles and user data (see GUIDATA)
global I0 A
I0_2=zeros(size(I0,1),size(I0,2));
for i=1:size(I0,1)
for j=1:size(I0,2)
if I0(i,j)==A(2)
I0_2(i,j)=255;
else I0_2(i,j)=0;
end
end
end
I0_2=uint8(I0_2);
axes(handles.axes4);
imshow(I0_2);
% --- Executes on button press in pushbutton5.
function pushbutton5_Callback(hObject, eventdata, handles)
% hObject handle to pushbutton5 (see GCBO)
% eventdata reserved - to be defined in a future version of MATLAB
% handles structure with handles and user data (see GUIDATA)
global I0 A
I0_3=zeros(size(I0,1),size(I0,2));
for i=1:size(I0,1)
for j=1:size(I0,2)
if I0(i,j)==A(3)
I0_3(i,j)=255;
else I0_3(i,j)=0;
end
end
end
I0_3=uint8(I0_3);
axes(handles.axes5);
imshow(I0_3);
% --- Executes on button press in pushbutton6.
function pushbutton6_Callback(hObject, eventdata, handles)
% hObject handle to pushbutton6 (see GCBO)
% eventdata reserved - to be defined in a future version of MATLAB
% handles structure with handles and user data (see GUIDATA)
global I0 A
I0_4=zeros(size(I0,1),size(I0,2));
for i=1:size(I0,1)
for j=1:size(I0,2)
if I0(i,j)==A(4)
I0_4(i,j)=255;
else I0_4(i,j)=0;
end
end
end
I0_4=uint8(I0_4);
axes(handles.axes6);
imshow(I0_4);
function varargout = CT_image_GFCM(varargin)
% CT_IMAGE_GFCM MATLAB code for CT_image_GFCM.fig
% CT_IMAGE_GFCM, by itself, creates a new CT_IMAGE_GFCM or raises the existing
% singleton*.
%
% H = CT_IMAGE_GFCM returns the handle to a new CT_IMAGE_GFCM or the handle to
% the existing singleton*.
%
% CT_IMAGE_GFCM('CALLBACK',hObject,eventData,handles,...) calls the local
% function named CALLBACK in CT_IMAGE_GFCM.M with the given input arguments.
%
% CT_IMAGE_GFCM('Property','Value',...) creates a new CT_IMAGE_GFCM or raises the
% existing singleton*. Starting from the left, property value pairs are
% applied to the GUI before CT_image_GFCM_OpeningFcn gets called. An
% unrecognized property name or invalid value makes property application
% stop. All inputs are passed to CT_image_GFCM_OpeningFcn via varargin.
%
% *See GUI Options on GUIDE's Tools menu. Choose "GUI allows only one
% instance to run (singleton)".
%
% See also: GUIDE, GUIDATA, GUIHANDLES
% Edit the above text to modify the response to help CT_image_GFCM
% Last Modified by GUIDE v2.5 13-Apr-2020 21:47:11
% Begin initialization code - DO NOT EDIT
gui_Singleton = 1;
gui_State = struct('gui_Name', mfilename, ...
'gui_Singleton', gui_Singleton, ...
'gui_OpeningFcn', @CT_image_GFCM_OpeningFcn, ...
'gui_OutputFcn', @CT_image_GFCM_OutputFcn, ...
'gui_LayoutFcn', [] , ...
'gui_Callback', []);
if nargin && ischar(varargin{1})
gui_State.gui_Callback = str2func(varargin{1});
end
if nargout
[varargout{1:nargout}] = gui_mainfcn(gui_State, varargin{:});
else
gui_mainfcn(gui_State, varargin{:});
end
% End initialization code - DO NOT EDIT
% --- Executes just before CT_image_GFCM is made visible.
function CT_image_GFCM_OpeningFcn(hObject, eventdata, handles, varargin)
% This function has no output args, see OutputFcn.
% hObject handle to figure
% eventdata reserved - to be defined in a future version of MATLAB
% handles structure with handles and user data (see GUIDATA)
% varargin command line arguments to CT_image_GFCM (see VARARGIN)
% Choose default command line output for CT_image_GFCM
handles.output = hObject;
% Update handles structure
guidata(hObject, handles);
% UIWAIT makes CT_image_GFCM wait for user response (see UIRESUME)
% uiwait(handles.figure1);
% --- Outputs from this function are returned to the command line.
function varargout = CT_image_GFCM_OutputFcn(hObject, eventdata, handles)
% varargout cell array for returning output args (see VARARGOUT);
% hObject handle to figure
% eventdata reserved - to be defined in a future version of MATLAB
% handles structure with handles and user data (see GUIDATA)
% Get default command line output from handles structure
varargout{1} = handles.output;
% --- Executes on button press in pushbutton1.
function pushbutton1_Callback(hObject, eventdata, handles)
% hObject handle to pushbutton1 (see GCBO)
% eventdata reserved - to be defined in a future version of MATLAB
% handles structure with handles and user data (see GUIDATA)
global I
[filename, pathname]= ...
uigetfile({'*.*';'*.bmp';'*.tif';'*.png';'*.jpg'},'select picture');
str= [pathname filename];
I= imread(str);
axes(handles.axes1);
imshow(I);
title('Original drawing');
% --- Executes on button press in pushbutton2.
function pushbutton2_Callback(hObject, eventdata, handles)
% hObject handle to pushbutton2 (see GCBO)
% eventdata reserved - to be defined in a future version of MATLAB
% handles structure with handles and user data (see GUIDATA)
global I
I=medfilt2(I,[3,3]);
axes(handles.axes2);
imshow(I)
% --- Executes on button press in pushbutton3.
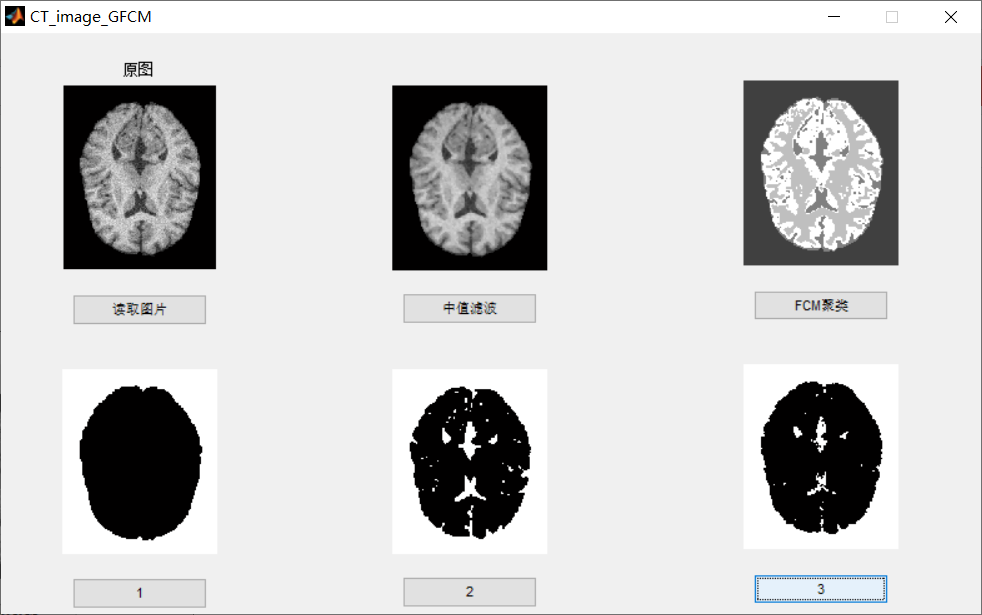
function pushbutton3_Callback(hObject, eventdata, handles)
% hObject handle to pushbutton3 (see GCBO)
% eventdata reserved - to be defined in a future version of MATLAB
% handles structure with handles and user data (see GUIDATA)
global I r c U
[r,c] = size(I);
data = zeros(r*c,1);
for i = 1:r
for j = 1:c
data((i-1)*c+j,1) = double(I(i,j));
end
end
[center, U, obj_fcn] = GFCM(data,4,0.9);
for i = 1 : r
for j = 1 : c
temp = (double(I(i, j)) - center) .^ 2;
[fmin pos] = min(temp);
I(i, j) = uint8(pos * 255 / 4);
end
end
axes(handles.axes3);
imshow(I)
% --- Executes on button press in pushbutton4.
function pushbutton4_Callback(hObject, eventdata, handles)
% hObject handle to pushbutton4 (see GCBO)
% eventdata reserved - to be defined in a future version of MATLAB
% handles structure with handles and user data (see GUIDATA)
global I r c U
I_seg2 = I*0;
for i = 1:r
for j = 1:c
if U(1,(i-1)*c+j)<U(2,(i-1)*c+j)
I_seg2(i,j) =0 ;
else
I_seg2(i,j) =255;
end
end
end
axes(handles.axes4);
imshow(I_seg2)
% --- Executes on button press in pushbutton5.
function pushbutton5_Callback(hObject, eventdata, handles)
% hObject handle to pushbutton5 (see GCBO)
% eventdata reserved - to be defined in a future version of MATLAB
% handles structure with handles and user data (see GUIDATA)
global I r c U
I_seg3 = I*0;
for i = 1:r
for j = 1:c
if U(1,(i-1)*c+j)<U(3,(i-1)*c+j)
I_seg3(i,j) =0 ;
else
I_seg3(i,j) =255;
end
end
end
axes(handles.axes5);
imshow(I_seg3)
% --- Executes on button press in pushbutton6.
function pushbutton6_Callback(hObject, eventdata, handles)
% hObject handle to pushbutton6 (see GCBO)
% eventdata reserved - to be defined in a future version of MATLAB
% handles structure with handles and user data (see GUIDATA)
global I r c U
I_seg4 = I*0;
for i = 1:r
for j = 1:c
if U(1,(i-1)*c+j)<U(4,(i-1)*c+j)
I_seg4(i,j) =0 ;
else
I_seg4(i,j) =255;
end
end
end
axes(handles.axes6);
imshow(I_seg4)
