🎈 Author: Linux ape
🎈 Introduction: CSDN blog expert 🏆, Huawei cloud sharing expert 🏆, C/C + +, interview, question brushing and algorithm. Please consult me, pay attention to me and chat privately if you have any questions!
🎈 Attention column: C/C + + interview customs collection (high quality articles are constantly updated...) 🚀
🎈 Welcome to praise 👍, Collection ⭐, Leaving a message. 💬
catalogue
1.3 array implementation stack
1.4 linked list implementation stack
one point six Complexity analysis
one point seven Application of stack
2.3 array implementation queue
2.4 linked list implementation queue
two point six Complexity analysis
two point seven Application of queue
In daily study and job interview, stack and queue are very important contents, which are often mentioned. This article summarizes the basic concepts and common operations of stack and queue, and realizes stack and queue by using array and linked list respectively. It is easy to understand and not difficult to think! Come and have a look!
1, Stack
1.1 what is stack
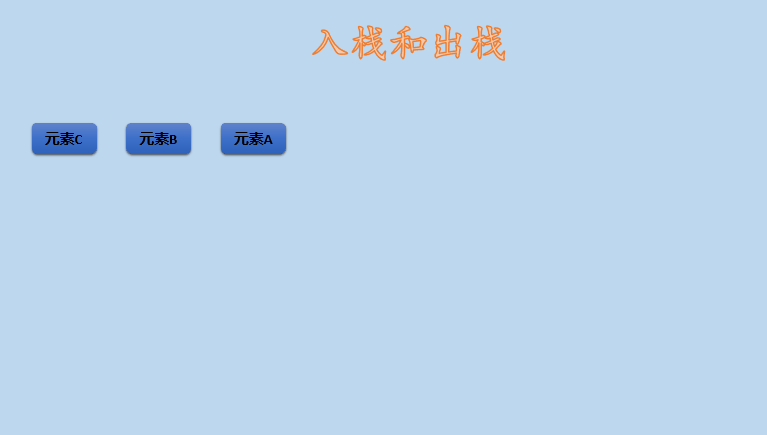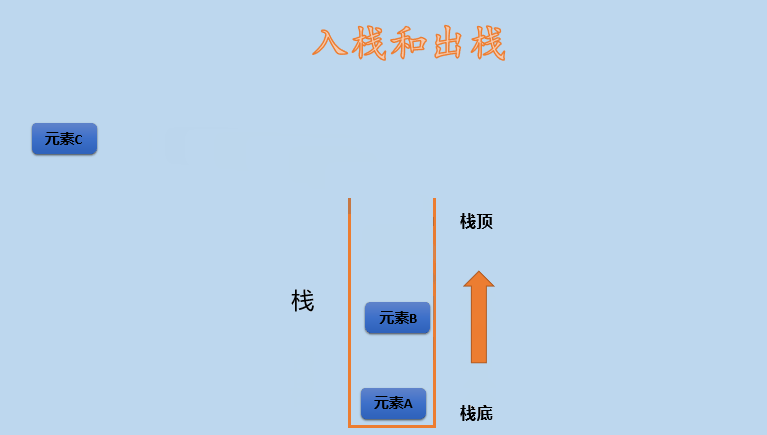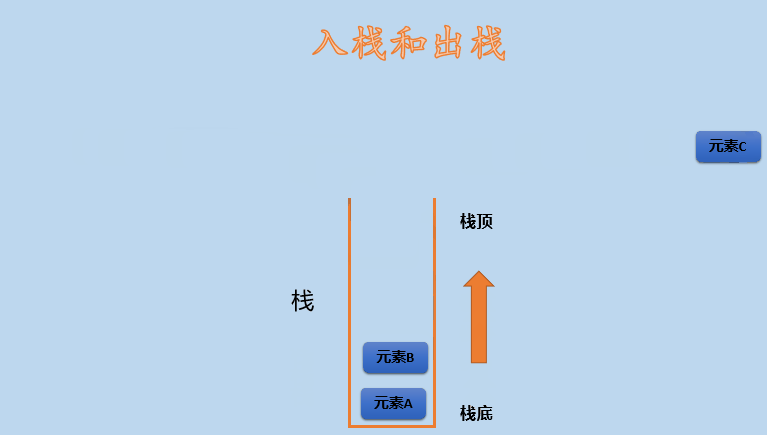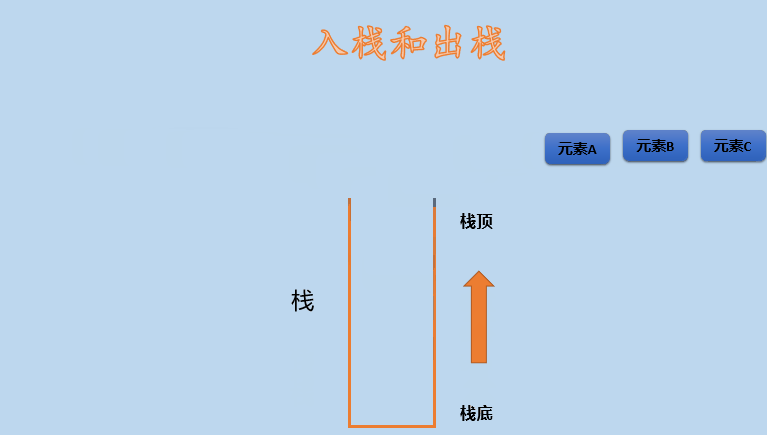
Stack is an abstract data structure and a linear data structure. It has the characteristics of LIFO (Last In First Out), that is, the elements in the last in stack are above the elements in the first out, so the elements in the last in stack are out of the stack first. Of course, it can also be said to be first in first out, that is, the elements in the first out are out of the stack later. The same principle, but different statements. As shown in the figure below:
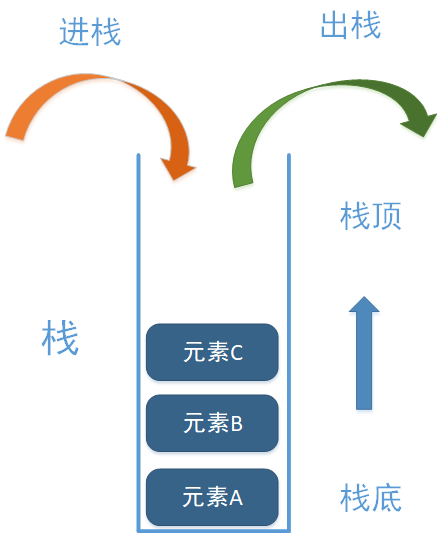
As can be seen from the above figure, the stack has only one entrance, that is, the entrance is also the exit. The element C that enters the stack last comes out of the stack first than B and A that enter the stack first. This is the so-called last in first out. As shown in the figure above, the stack has A top and A bottom.
Take a look at the dynamic diagram, as shown below:
 title
title
1.2 implementation mode
Stack can be realized by array or linked list, as shown in the following figure:
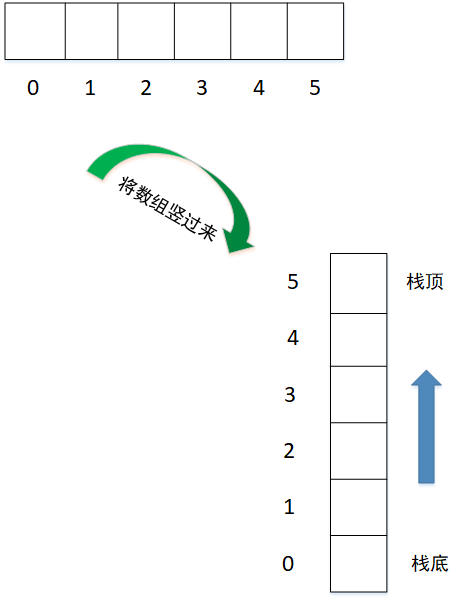 title
title
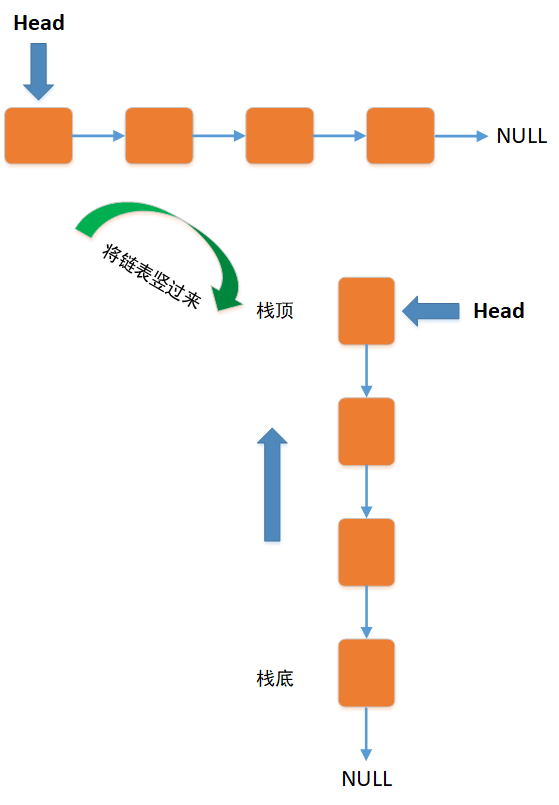 title
title
Let's take a look at arrays and linked lists to implement stacks.
1.3 array implementation stack
Class 1.3.0 package
The following encapsulates the common operations of the stack with classes, as follows:
#define NUM 100000 / / stack size
class Stack {
int data[NUM]; // Array simulation stack
int num; // Stack pointer to the top element of the stack
public:
Stack() { // initialization
num = -1;
memset(data, 0, sizeof(data));
}
void push(int val); // Add element
int pop(); // Delete stack top element
int top(); // Return stack top element
bool empty(); // Judge whether it is empty
int size(); // Stack size
};The above example is int. the better encapsulation is to use the C + + template. Here, a simpler method is adopted for ease of understanding.
On the other hand, the array can also be changed to the form of dynamic allocation, that is, an initial array is allocated first. If the stack overflows, it will be reallocated and the original content will be copied to the newly allocated array. The allocation method can refer to the incremental strategy of STL.
1.3.1 push operation
Add elements to the stack as follows:
void Stack::push(int val) {
if(num >= NUM) {
cout<<"Stack Overflow!"<<endl;
return;
}
data[++num] = val;
}As shown above, first judge whether the stack is full, and if not, add elements. You can modify the contents of the above if statement to increase the stack capacity.
1.3.2 pop operation
Delete the stack top element because the stack is last in first out, as shown below:
int Stack::pop() {
if(empty()) {
cout<<"Stack Empty!"<<endl;
return -1;
}
return data[num--];
}As shown above, first judge whether the stack is empty. If it is not empty, delete the stack top element as long as the stack top pointer moves.
1.3.3 empty operation
Judge whether the stack is empty. If it is empty, return true; otherwise, return false, as shown below:
bool Stack::empty() {
return num == -1;
}Someone might say, "why not use int type and return 0 and 1? It is better to use true and false because bool type takes up one byte, while int usually takes up four bytes.
1.3.4 top operation
Return the stack top element as follows:
int Stack::top() {
if(empty()) {
cout<<"Stack Empty!"<<endl;
return -1;
}
return data[num];
}First judge whether the stack is empty. If it is not empty, return the top element of the stack.
Note: This is not a deletion, it just returns the value of the top element of the stack.
1.3.5 size operation
Returns the stack size as follows:
int Stack::size() {
return num + 1;
}The stack pointer num starts from 0, so num+1 is returned.
1.3.6 array stack test
The following is to test the above array stack implementation, as shown below:
int main()
{
Stack st;
st.push(10);
st.push(20);
cout<<"The size of stack is "<<st.size()<<endl;
cout<<"The top of stack is "<<st.top()<<endl;
cout<<"The stack empty is "<<st.empty()<<endl;
cout<<"----------------------------------------"<<endl;
st.pop();
cout<<"The size of stack is "<<st.size()<<endl;
cout<<"The top of stack is "<<st.top()<<endl;
cout<<"----------------------------------------"<<endl;
st.clear();
cout<<"The stack empty is "<<st.empty()<<endl;
cout<<"The size of stack is "<<st.size()<<endl;
return 0;
}Output is:
The size of stack is 2 The top of stack is 20 The stack empty is 0 ---------------------------------------- The size of stack is 1 The top of stack is 10 ---------------------------------------- The stack empty is 1 The size of stack is 0
1.4 linked list implementation stack
Class 1.4.0 package
Use class to encapsulate the stack, as shown below:
struct node { // Linked list single node
int val; // Stack element value
struct node* next;// Pointer to the next element
node(int value) { // Initial value assignment
val = value;
}
};
class Stack {
struct node *index; // Point to stack top element
int s_size; // Record stack capacity
public:
Stack() { // initialization
index = nullptr;
s_size = 0;
}
~Stack() ;
void push(int val); // Add element
int pop(); // Delete stack top element
int top(); // Return stack top element
bool empty(); // Judge whether it is empty
int size(); // Stack size
};Struct node is a single element in the linked list. class Stack contains various operations of the stack. Here, s_size is used to record the capacity of the stack for easy operation. Of course, int is taken as an example, which can be modified into the template form of C + +.
1.4.1 push operation
Add elements to the stack as follows:
void Stack::push(int val) {
struct node* tmp = new node(val);
if(tmp == nullptr) {
cout<<"Failed to allocate space!"<<endl;
return;
}
tmp->next = index;
index = tmp;
s_size++;
}As shown above, it is not necessary to judge whether the stack is full, but to judge whether an allocation is successful.
1.4.2 pop operation
Delete the stack top element because the stack is last in first out, as shown below:
int Stack::pop() {
if(empty()) {
cout<<"Stack Empty!"<<endl;
return -1;
}
int tmpVal = index->val; // Temporary stack top element
index = index->next; // Delete stack top element
s_size--; // Number of stack elements minus one
return tmpVal; // This returns the lower stack top element
}As shown above, first judge whether the stack is empty. If it is not empty, delete the stack top element as long as the stack top pointer moves.
1.4.3 empty operation
Judge whether the stack is empty. If it is empty, return true; otherwise, return false, as shown below:
bool Stack::empty() {
return index == nullptr;
}1.4.4 top operation
Return the stack top element as follows:
int Stack::top() {
if(empty()) {
cout<<"Stack Empty!"<<endl;
return -1;
}
return index->val; // Returns only the top element of the stack
}Because index always points to the top element of the stack, it directly returns index - > val.
1.4.5 size operation
Returns the stack size as follows:
int Stack::size() {
return s_size;
}Here, s_size is used to record the stack size, otherwise the linked list will be traversed every time.
1.4.6 linked list stack test
The following is to test the implementation of the above linked list stack, as shown below:
int main()
{
Stack st;
st.push(10);
st.push(20);
cout<<"The size of stack is "<<st.size()<<endl;
cout<<"The top of stack is "<<st.top()<<endl;
cout<<"The stack empty is "<<st.empty()<<endl;
cout<<"----------------------------------------"<<endl;
st.pop();
cout<<"The size of stack is "<<st.size()<<endl;
cout<<"The top of stack is "<<st.top()<<endl;
cout<<"----------------------------------------"<<endl;
st.clear();
cout<<"The stack empty is "<<st.empty()<<endl;
cout<<"The size of stack is "<<st.size()<<endl;
return 0;
}
Output is:
linuxy@linuxy:~/Stack$ g++ -o main Stack.cpp linuxy@linuxy:~/Stack$ ./main The size of stack is 2 The top of stack is 20 The stack empty is 0 ---------------------------------------- The size of stack is 1 The top of stack is 10 ---------------------------------------- The stack empty is 1 The size of stack is 0 linuxy@linuxy:~/Stack$
1.5 actual combat analysis
Simulate the operation of element stack and how to realize the following stacking order to the stacking order.
Stack order: A B C D
Stack out sequence: C B D A
Let's look at the following diagram:
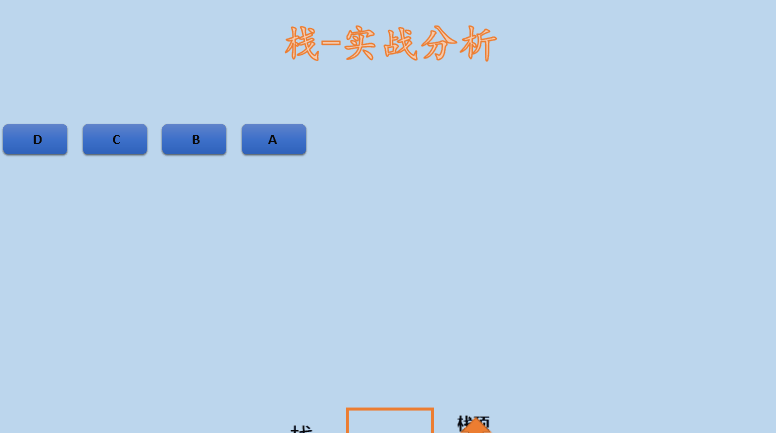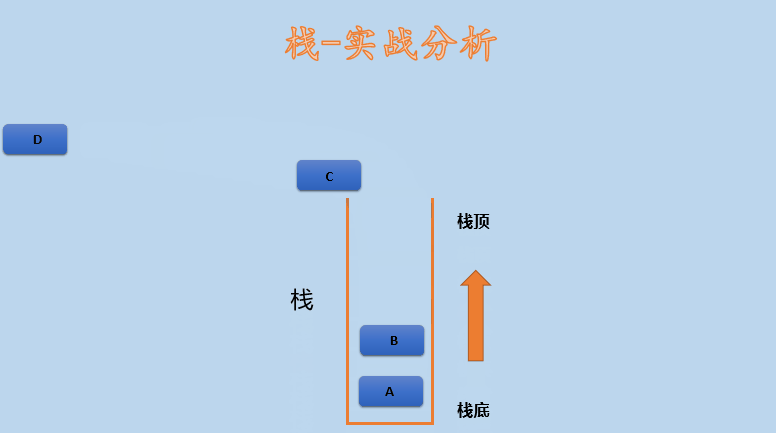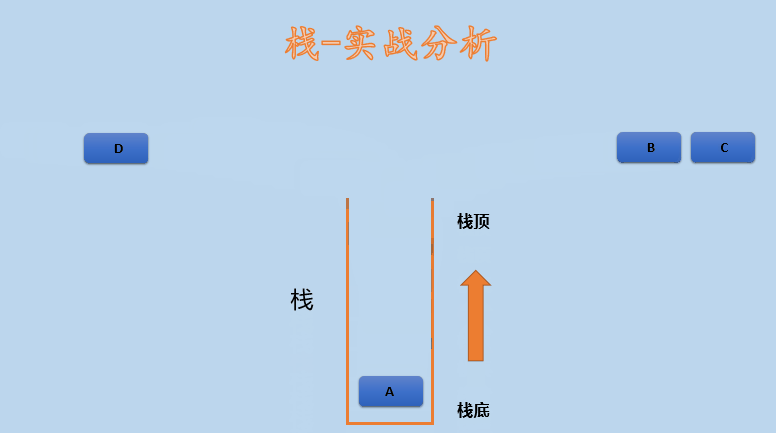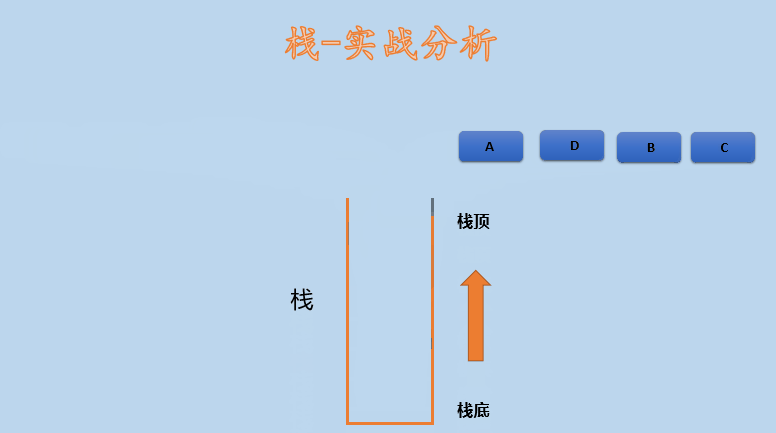
one point six Complexity analysis
1.6.1 time complexity
The time complexity of push and pop operations is O(1) regardless of the stack implemented by linked list or array. The clear operation in the stack implemented by linked list is O(n), because all linked list space needs to be released, and other operations are O(1).
1.6.2 space complexity
The linked list saves more space than the array, because the linked list will not be allocated until it is used. The array is allocated in advance, and if the stack is full, the array needs to be reallocated.
one point seven Application of stack
(1) Depth first search
The non recursive implementation of depth first search usually uses stack as an auxiliary array structure.
(2) Fallback and forward functions in software
(3) Topological sorting
2, Queue
2.1 what is a queue
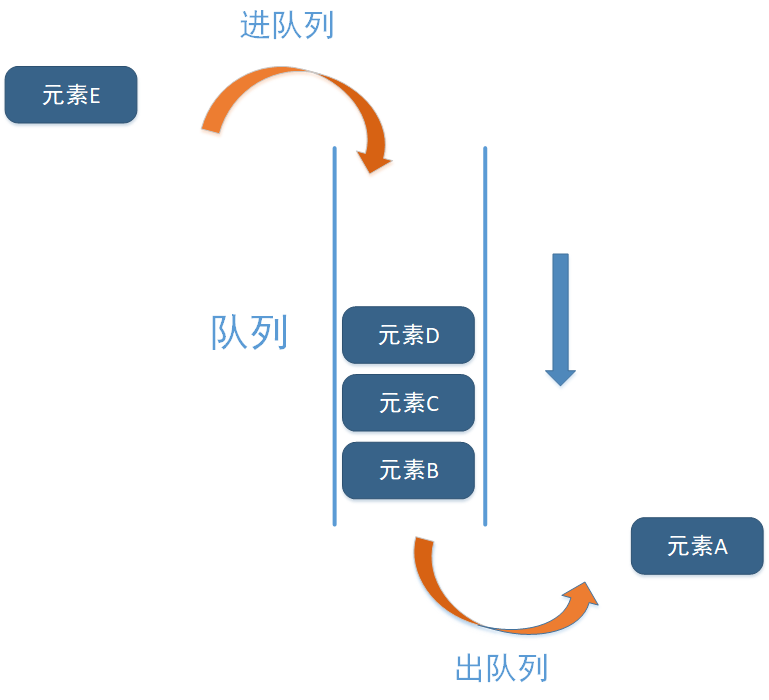
Queue is an abstract data type with linear structure, which can realize FIFO (First In, First Out), that is, the First In element and the First Out queue, which can be compared to daily queuing to buy things.
As shown in the figure below:
 title
title
As can be seen from the above figure, the queue is different from the stack. The queue has two ports. One is only allowed to enter the element, the other is only allowed to exit the element, and the last in and last in element C is out of the stack first than the first in B and A. this is the so-called last in first out. As shown in the figure above, the stack has A top and A bottom.
Take a look at the dynamic diagram, as shown below:
 title
title
2.2 implementation mode
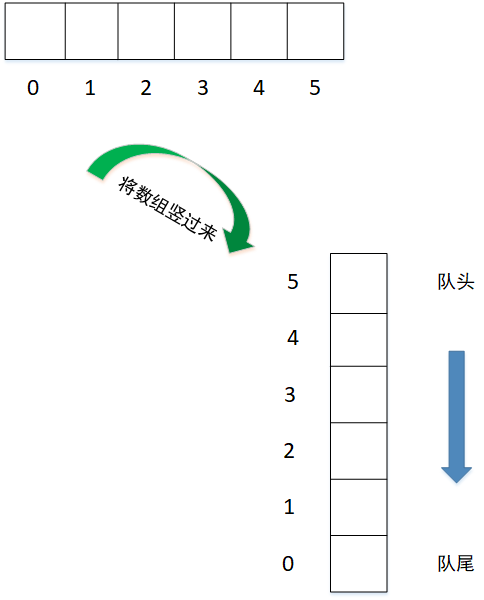
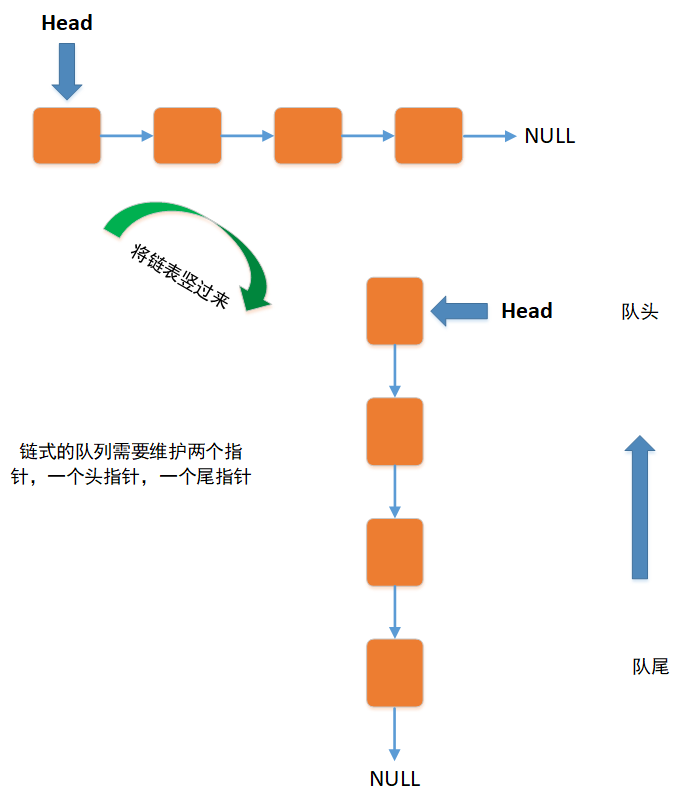
Queues can be implemented through arrays or linked lists, as shown in the following figure:
 title
title
 title
title
2.3 array implementation queue
Class 2.3.0 package
The following is an example of encapsulating a queue with a class, as follows:
#define NUM 100000 / / queue size
class Queue {
int data[NUM]; // Array emulation queue
int first; // Header pointer to the top of the queue
int last; // Tail pointer to the tail of the queue
public:
Queue() { // initialization
first = 0;
last = 0;
memset(data, 0, sizeof(data));
}
void push(int val); // Add element
int pop(); // Delete queue header element
int front(); // Returns the queue header element
bool empty(); // Judge whether it is empty
int size(); // Queue size
int back(); // Returns the end of queue element
};Data stores queue data. first and last point to the head and tail of the queue respectively.
2.3.1 push operation
Add an element to the queue as follows:
void Queue::push(int val) {
if(last >= NUM) {
cout<<"Queue Overflow!"<<endl;
return;
}
data[last++] = val;
}First judge whether the queue is full. If it is not full, add elements. To add elements, you only need to move the tail pointer.
2.3.2 pop operation
Delete the queue header element as follows:
int Queue::pop() {
if(empty()) {
cout<<"Queue Empty!"<<endl;
return -1;
}
return data[first++];
}As shown above, first judge whether the queue is empty. If it is not empty, delete the queue header element and just move the header pointer first.
2.3.3 front operation
The principle of returning the value of the header element is the same as the top operation of the stack, as shown below:
int Queue::front() {
if(empty()) {
cout<<"Queue Empty!"<<endl;
return -1;
}
return data[first];
}First judge whether the queue is empty. If it is not empty, the header element is returned.
2.3.4 empty operation
Judge whether the queue is empty, as shown below:
bool Queue::empty() {
return first == last;
}Directly compare whether first and last are equal.
2.3.5 size operation
Judge the number of queue elements as follows:
int Queue::size() {
return last - first;
}The example before using the tail pointer and the head pointer of the queue is the number of elements.
2.3.6 back operation
Return the end of queue element as follows:
int Queue::back() {
if(empty()) {
cout<<"Queue Empty!"<<endl;
return -1;
}
return data[last-1];
}First judge whether it is empty. If it is not empty, return the element where last - 1 is located, because last points to the next position of the tail element.
2.3.7 array queue test
The following is a test of the queue implemented by the above array, as shown below:
int main()
{
Queue que;
cout<<"The queue empty is "<<que.empty()<<endl;
cout<<"The size of queue is "<<que.size()<<endl;
cout<<"----------------------------------------"<<endl;
que.push(10);
que.push(20);
cout<<"The size of queue is "<<que.size()<<endl;
cout<<"The front of queue is "<<que.front()<<endl;
cout<<"The queue empty is "<<que.empty()<<endl;
cout<<"----------------------------------------"<<endl;
que.pop();
cout<<"The size of queue is "<<que.size()<<endl;
cout<<"The front of queue is "<<que.front()<<endl;
return 0;
}Output is:
linuxy@linuxy:~/Stack$ ./main The queue empty is 1 The size of queue is 0 ---------------------------------------- The size of queue is 2 The front of queue is 10 The queue empty is 0 ---------------------------------------- The size of queue is 1 The front of queue is 20 linuxy@linuxy:~/Stack$
2.4 linked list implementation queue
Class 2.4.0 package
struct node { // struct Node
int val; // Linked list value
struct node* next;
node(int value) {
val = value;
}
};
class Queue {
struct node *first; // Point to queue header element
struct node *rear; // Point to end of queue element
int s_size; // Number of record queue elements
public:
Queue() { // initialization
first = nullptr;
rear = nullptr;
s_size = 0;
}
~Queue();
void push(int val); // Add element
int pop(); // Delete queue header element
int front(); // Returns the queue header element
bool empty(); // Judge whether it is empty
int size(); // Number of queue elements
void back(); // Returns the end of queue element
};first points to the queue header element, rear points to the queue tail element, s_size records the number of elements in the queue.
2.4.1 push operation
Add elements to the queue and add them to the end of the queue, because the queue is first in first out, as shown below:
void Queue::push(int val) {
struct node* tmp = new node(val);
if(tmp == nullptr) {
cout<<"Failed to allocate space!"<<endl;
return;
}
if(rear == nullptr) { // Add first element
first = tmp;
rear = tmp;
tmp->next = nullptr;
} else { // Existing element
rear->next = tmp;
tmp->next = nullptr;
rear = tmp;
}
s_size++;
}Here, you need to allocate space first. When adding an element for the first time, you need to point to both first and rear, otherwise you can add it to the tail. Don't forget to add s_size.
2.4.2 pop operation
Delete the queue header element as follows:
int Queue::pop() {
if(empty()) {
cout<<"Stack Empty!"<<endl;
return -1;
}
struct node* tmp = first;
first = first->next;
int val = tmp->val;
delete tmp;
s_size--;
return val;
}First judge whether the queue is empty. If not, move the queue header pointer and don't forget to free space.
2.4.3 front operation
Return the value of the queue header element, not delete! As follows:
int Queue::front() {
if(empty()) {
cout<<"Stack Empty!"<<endl;
return -1;
}
return first->val;
}The front of the queue is similar to the top of the stack.
2.4.4 empty operation
Judge whether the queue is empty, as shown below:
bool Queue::empty() {
return first == nullptr;
}2.4.5 size operation
Judge the number of queue elements as follows:
int Queue::size() {
return s_size;
}An auxiliary variable s is used here_ Otherwise, you need to traverse the linked list every time you find the number of queue elements.
2.4.6 linked list queue test
The following is to test the implementation of the above linked list queue, as shown below:
int main()
{
Queue que;
cout<<"The queue empty is "<<que.empty()<<endl;
cout<<"The size of queue is "<<que.size()<<endl;
cout<<"----------------------------------------"<<endl;
que.push(10);
que.push(20);
cout<<"The size of queue is "<<que.size()<<endl;
cout<<"The top of queue is "<<que.front()<<endl;
cout<<"The queue empty is "<<que.empty()<<endl;
cout<<"----------------------------------------"<<endl;
que.pop();
cout<<"The size of queue is "<<que.size()<<endl;
cout<<"The top of queue is "<<que.front()<<endl;
cout<<"----------------------------------------"<<endl;
return 0;
}The output result is:
linuxy@linuxy:~/Queue$ ./main The queue empty is 1 The size of queue is 0 ---------------------------------------- The size of queue is 2 The top of queue is 10 The queue empty is 0 ---------------------------------------- The size of queue is 1 The top of queue is 20 ---------------------------------------- linuxy@linuxy:~/Queue$
2.5 actual combat analysis
The hierarchical traversal method is adopted to traverse the following binary tree:
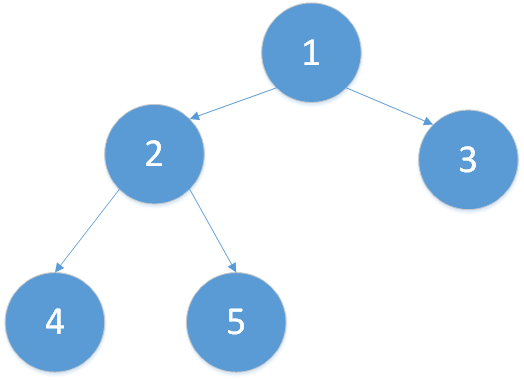 title
title
Let's take a look at the dynamic diagram:
 title
title
two point six Complexity analysis
2.6.1 time complexity
The time complexity of push, pop, empty, front and other operations is O(1) regardless of the queue implemented by linked list or array.
2.6.2 space complexity
The linked list saves more space than the array, because the linked list will not be allocated until it is used. The array is allocated in advance, and if the queue is full, the array needs to be reallocated.
two point seven Application of queue
(1) Breadth first search
The implementation of breadth first search usually uses queue as an auxiliary array structure.
(2) In some resource requests or task scheduling, they are often processed first come first.
3, Summary
Stack and queue have strong characteristics. Stack is last in first out and queue is first in first out. They are applied in different application scenarios.
Welcome to the following 👇👇👇 official account 👇👇👇, Get more quality content 🤞 (comparison)!