1. Polymorphism

1. First acquaintance

What is polymorphism? Generally speaking, "one form has many forms", this answer will certainly not be satisfactory. The following code will tell you what polymorphism is

class Animal{
    public String name;
    public int age;
}
class Dog extends Animal{
}

class Bird extends Animal{
}

public class TestDemo {
    private static void test(){
        Dog dog = new Dog();// Create a dog object normally
        Animal animal = new Dog();// An Animal type reference points to the Dog object

		// Bird can also
		Animal animal1 = new Bird();
    }

    public static void main(String[] args) {
        test();
    }
}

1. We found that the new Dog() object can be pointed not only by the Dog type reference, but also by its parent Animal type reference
2. Parent variables store child variables, which means "one form and multiple forms" at the beginning. An Animal type variable can store cats, dogs, birds and other animals

Think: can Bird point to Dog?

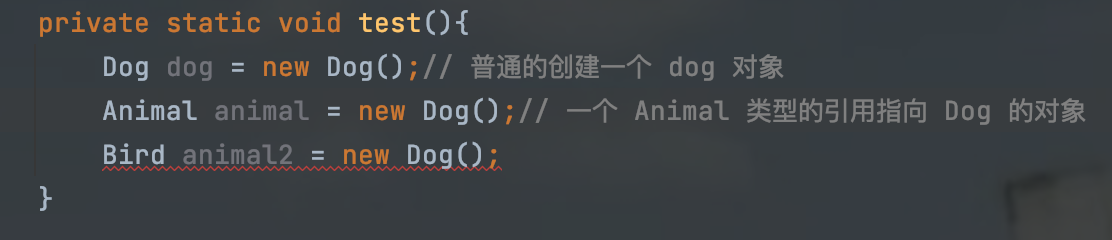
We found that IDEA has prompted us with errors
The reason is: Dog and Bird are incompatible. For example, can a Dog be a Bird? This must be breaking the laws of nature, so you can't point at the Dog and say it's a Bird. The compiler also cannot point the Bird class to the Dog class. Only their parent Animal can point to Dog, Bird and other Animal classes.

2. Upward transformation

class Animal{
    String name = "Animal";
    int age = 1;

    Animal(String name) {
        this.name = name;
    }

    void eat(){
        System.out.println(this.name + "Animal:eat()");
    }
}
class Dog extends Animal{
    Dog(String name) {
        super(name);
    }

    void eat(){
        System.out.println(this.name + "Dog:eat()");
    }
}

class Bird extends Animal{
    Bird(String name) {
        super(name);
    }

    void eat(){
        System.out.println(this.name + "Bird:eat()");
    }
}

public class TestDemo {
    private static void test(){
        Dog dog = new Dog("Erha");
        dog.eat();
        Animal animal = new Dog("Erha");
        animal.eat();
    }

    public static void main(String[] args) {
        test();
    }
}

Erha Dog:eat()
Erha Dog:eat()

Here, we add a construction method to give each class a name="Animal" and age=1 member data. We output the eat method to see the results
We found that no matter whether dog or animal's eat method is called, it is the eat method of dog class

// Generate a Dog reference object, which can be written as follows
Dog dog = new Dog("Erha");
// The code above can also be written like this
Dog dog1 = new Dog("Erha");
Animal animal = dog1;// Or it can be simplified to: Animal animal = new Dog("erha"); [recommended]

1. At this time, dog1 is a reference to the parent class (Animal) and points to an instance of the child class (Bird). This writing is called upward transformation
2. Upward transformation can be understood in combination with is - a semantics
3. For example, I said, "did you feed the dog today?" or "did you feed erha today?". Because erha is indeed a dog and an animal

3. Method of upward transformation

1. Direct assignment

Above examples

  Dog dog = new Dog("Erha");
  Animal animal = new Dog("Erha");

Is direct assignment

2. Method transmission

public class TestDemo {

    private static void test_eat(Animal animal){
        animal.eat();
    }
    private static void test(){
        Dog dog = new Dog("Erha");
        test_eat(dog);
        Animal animal = new Dog("Erha");
        test_eat(animal);
    }

    public static void main(String[] args) {
        test();
    }
}

At this time, the type of formal parameter Animal is Animal (base class), which actually corresponds to the instance of dog (parent class)

3. Method return

public class TestDemo {
    public static Animal findMyAnimal() {
        Dog dog = new Dog("Erha");
        return dog;
    }

    private static void test_eat(Animal animal) {
        animal.eat();
    }

    private static void test() {
        test_eat(findMyAnimal());
    }

    public static void main(String[] args) {
        test();
    }
}
Erha Dog:eat()

At this time, the method findMyAnimal returns a reference of Animal type, but actually corresponds to the instance of Bird

4. Dynamic binding

When it comes to polymorphism, it is inseparable from upward transformation, and the operation result of upward transformation is inseparable from dynamic binding.

The source code is as follows:

class Animal {
    String name = "Animal";
    int age = 1;

    Animal(String name) {
        this.name = name;
    }

    void eat() {
        System.out.println(this.name + "Animal:eat()");
    }
}

class Dog extends Animal {
    Dog(String name) {
        super(name);
    }

    void eat() {
        System.out.println(this.name + "Dog:eat()");
    }
}

class Bird extends Animal {
    Bird(String name) {
        super(name);
    }

    void eat() {
        System.out.println(this.name + "Bird:eat()");
    }
}

public class TestDemo {
    public static void main(String[] args) {
        Animal animal = new Dog("Erha");
        animal.eat();
    }
}

The assembly code is as follows:

cxf@cxfdeMacBook-Pro Gao % javap -c TestDemo
 warning: Binary file TestDemo contain bit.basis.Gao.TestDemo
Compiled from "TestDemo.java"
public class bit.basis.Gao.TestDemo {
  public bit.basis.Gao.TestDemo();
    Code:
       0: aload_0
       1: invokespecial #1                  // Method java/lang/Object."<init>":()V
       4: return

  public static void main(java.lang.String[]);
    Code:
       0: new           #2                  // class bit/basis/Gao/Dog
       3: dup
       4: ldc           #3 / / string erha
       6: invokespecial #4                  // Method bit/basis/Gao/Dog."<init>":(Ljava/lang/String;)V
       9: astore_1
      10: aload_1
      11: invokevirtual #5                  // Method bit/basis/Gao/Animal.eat:()V
      14: return
}
cxf@cxfdeMacBook-Pro Gao % 

1. among invokespecial It refers to calling instance methods that do not need dynamic binding [calling instance methods; special processing for super class, private and instance initialization method calls], which is easy to understand, that is, calling the constructor of the parent class
2. The program starts from the main function, so it will first construct the constructor of the parent class, that is, the constructor of Object without parameters [1: invokespecial #1 // Method java/lang/Object."": ()V]
3. The internal construction method of the program is Dog [6: invokespecial #4 / / method bit / basis / Gao / Dog. ": (ljava / Lang / string;) v]
4. The program calls the of Animal. eat() function [11: invokevirtual #5 // Method bit/basis/Gao/Animal.eat:()V]

Why does the Dog.eat(0) method print out when the function of Animal.eat() is called?

Erha Animal:eat()

But it printed out

Erha Dog:eat()

This is the dynamic binding explained above - call the instance method without dynamic binding, and Dog.eat() needs dynamic binding, so it will call the method of the parent class Animal.eat(), and then the JVM will deal with the method of the subclass in a special way at runtime, so it will print out

Erha Dog:eat()

Such unexpected results.

Therefore, in Java, which code (which is the code of the parent class method or the code of the subclass method) is executed by calling a class method, depends on whether the reference refers to the parent class object or the subclass object. This procedure is determined by the program runtime (instead of the compile period), so it is called dynamic binding.

5. Method rewriting

For the eat method just now:
The subclass implements the method with the same name as the parent class, and the type and number of parameters are exactly the same. This situation is called override
Notes on rewriting

1. Rewriting and overloading are completely different. Don't confuse (think about it, what are the rules of overloading?)
2. Ordinary methods can be overridden, but static methods modified by static cannot be overridden
3. Overriding a subclass's method cannot have lower access than the parent's method
4. The return value type of the overridden method may not be the same as that of the parent class (but it is recommended to write it the same, except in special cases)

Example of method permission: change eat of subclass to private

class Animal {
    String name = "Animal";
    int age = 1;

    Animal(String name) {
        this.name = name;
    }

    void eat() {
        System.out.println(this.name + "Animal:eat()");
    }
}

class Dog extends Animal {
    Dog(String name) {
        super(name);
    }

    private eat() {
        System.out.println(this.name + "Dog:eat()");
    }
}
Dog Medium eat()Cannot overwrite bit.basis.Gao.Animal Medium eat()Attempting to assign lower access rights; Previously package

In addition, for rewritten methods, the @ Override annotation can be used to display the specified [shortcut key: command+o or ctr+o]

class Bird extends Animal {
    Bird(String name) {
        super(name);
    }

    @Override
    void eat() {
        System.out.println(this.name + "Bird:eat()");
    }
}

With this annotation, we can check the validity. If we accidentally write eat as ate, the compiler will find that there is no ate method in the parent class, and an error will be reported indicating that the rewrite cannot be completed
It is recommended to explicitly add the @ Override annotation when overriding methods in code

6. Difference between overloading and rewriting

No	difference	Overload	Override
1	concept	The method name is the same, the number and type of parameters are different, and the return value is not required	The method name is the same, the number and type of parameters are the same, and the return value should be the same as far as possible
2	Range	A class	In inheritance relationship
3	limit	No permission requirements	Overridden methods cannot have more stringent access control permissions than the parent class

In fact, method rewriting is a rule at the Java syntax level, and dynamic binding is the underlying implementation of the syntax rule of method rewriting. They essentially describe the same thing, but have different emphases

7. Understanding polymorphism

With face up transformation, dynamic binding and method rewriting, we can design programs in the form of polymorphism
We can write some code that only focuses on the parent class, which can be compatible with various subclasses at the same time
Code example: print multiple shapes

class Shape{
    void draw(){
    }
}

class Cycle extends Shape{
    @Override
    void draw() {
        System.out.println("Draw a circle");
    }
}

class Rect extends Shape{
    @Override
    void draw() {
        System.out.println("Draw a rectangle");
    }
}

class Flower extends Shape{
    @Override
    void draw() {
        System.out.println("Draw a flower");
    }
}
public class TestDemo {
    private static void func(Shape s){
        s.draw();
    }
    private static void test(){
        Shape[] shapes = new Shape[]{new Cycle(), new Rect(), new Flower()};
        for (Shape s: shapes) {
            func(s);
        }
    }
    public static void main(String[] args) {
        test();
    }
}

Draw a circle
 Draw a rectangle
 Draw a flower

1. Create a parent Shape and write a draw method without doing anything
2. If you create some pattern classes and inherit the parent class Shape, each child class will have a draw method
3. Each subclass overrides the draw method
4. The formal parameter of func function is of Shape type. s of foreach loop in test function will enter Shape for upward transformation
5. Each subclass overrides the draw method to bind dynamically when running s.draw(), regardless of whether the types are compatible

When the caller of a class writes the draw method, the parameter type is shape (parent class). At this time, he does not know or pay attention to the instance of which type (subclass) the current shape reference points to. At this time, the reference of shape may call the draw method in many different ways (related to the instance corresponding to shape), This behavior is called polymorphism

Polymorphism, as the name suggests, is "a reference that can show many different forms"

8. Benefits of polymorphism

1. The cost of using classes by class callers is further reduced

• Encapsulation is to make the caller of a class not need to know the implementation details
• Polymorphism allows the caller of a class to know a method of an object without considering the type of the class
  Therefore, it can be understood that polymorphism is a further step of encapsulation, which further reduces the cost of using the class by the caller of the class

2. It can reduce the "circle complexity" of the code and avoid using a large number of if - else

If else matching is required for the following printed shapes

    private static void test() {
        Rect rect = new Rect();
        Cycle cycle = new Cycle();
        Flower flower = new Flower();
        String[] shapes = {"cycle", "rect", "cycle", "rect", "flower"};
        for (String shape : shapes) {
            if (shape.equals("cycle")) {
                cycle.draw();
            }else if (shape.equals("rect")){
                rect.draw();
            }else if (shape.equals("flower")){
                flower.draw();
            }
        }
    }

If you switch to polymorphism, you only need one line of code to solve it

private static void func(Shape s) {
        s.draw();
    }

    private static void test() {
        Rect rect = new Rect();
        Cycle cycle = new Cycle();
        Flower flower = new Flower();
        String[] shapes = {"cycle", "rect", "cycle", "rect", "flower"};
        for (String shape : shapes) {
            if (shape.equals("cycle")) {
                cycle.draw();
            }
        }
    }

What is "circle complexity"?

Circle complexity is a way to describe the complexity of a piece of code. If a piece of code is flat and straightforward, it is relatively simple and easy to understand. If there are many conditional branches or loop statements, it is considered more complex to understand. Therefore, we can simply and roughly calculate the number of conditional statements and loop statements in a piece of code, which is called "circle complexity" If the cyclomatic complexity of a method is too high, you need to consider refactoring
Different companies have different specifications for the cyclomatic complexity of code. Generally, it will not exceed 10

3. Stronger scalability

If you want to add a new shape, the code change cost is low by using polymorphism

class Triangel extends Shape{
    @Override
    void draw() {
        System.out.println("Draw a triangle");
    }
}

• For the caller of the class (drawShapes method), just create an instance of the new class, and the change cost is very low
• In the case of no polymorphism, the if - else in drawShapes must be modified, and the change cost is higher

9. Downward transformation

Upward transformation means that a child object is transformed into a parent object; Downward transformation means that the parent object is transformed into a character object. Compared with upward transformation, downward transformation is not used much, but it also has certain uses

package bit.basis.Gao;

class Animal {
    String name;

    Animal(String name) {
        this.name = name;
    }

    void eat(String food) {
        System.out.println("Animal:eat()" + this.name + food);
    }
}

class Bird extends Animal {
    Bird(String name) {
        super(name);
    }

    void eat(String food) {
        System.out.println("Bird:eat()" + this.name + food);
    }

    void fly() {
        System.out.println("Bird:fly()" + this.name + "Flying");
    }
}

public class TestDemo {

    public static void main(String[] args) {
        Animal animal = new Bird("parrot");
        animal.eat("food");
    }
}

We let animal fly

animal.fly();
// Compilation error
java: Symbol not found
  Symbol:   method fly()
  position: Type is bit.basis.Gao.Animal Variable of animal

matters needing attention
During the compilation process, the type of Animal is Animal. At this time, the compiler only knows that there is an eat method in this class and no fly method. Although Animal actually refers to a Bird object, the compiler uses the type of Animal to see which methods are available. For codes such as Animal animal = new Bird("parrot")

• The compiler checks which methods exist and which Animal types are checked
• Whether the parent or child methods are executed depends on the type Bird

Therefore, if you want the above code to achieve the effect just now, you must make a downward transformation

Bird bird = (Bird) animal;
bird.fly();

// results of enforcement
Bird:eat()Parrot Food// Call the eat method and run the eat method of the child class instead of the eat method of the parent class
Bird:fly()The parrot is flying

But such a downward transformation is not reliable, for example

class Animal {
    String name;

    Animal(String name) {
        this.name = name;
    }

    void eat(String food) {
        System.out.println("Animal:eat()" + this.name + food);
    }
}

class Bird extends Animal {
    Bird(String name) {
        super(name);
    }

    void eat(String food) {
        System.out.println("Bird:eat()" + this.name + food);
    }

    void fly() {
        System.out.println("Bird:fly()" + this.name + "Flying");
    }
}

class Cat extends Animal{
    Cat(String name) {
        super(name);
    }

    @Override
    void eat(String food) {
        System.out.println("Cat:eat()" + this.name + food);
    }
}

public class TestDemo {

    public static void main(String[] args) {
        Animal animal = new Cat("Mimi");
        Bird bird = (Bird) animal;
        bird.fly();
    }
}

// Run error
Exception in thread "main" java.lang.ClassCastException

animal essentially refers to a Cat object and cannot be converted into a Bird object. An exception will be thrown at runtime
Therefore, in order to make the downward transformation safer, we can first determine whether animal is essentially a Bird instance, and then convert

    public static void main(String[] args) {
        Animal animal = new Cat("Mimi");
        if (animal instanceof Bird) {
            Bird bird = (Bird) animal;
            bird.fly();
        }
    }

// No error during operation

instanceof can determine whether a reference is an instance of a class. If so, it returns true. At this time, it is safe to conduct downward transformation

10.super keyword

In the previous code, due to the rewriting mechanism, the methods of the subclass are called. What if you need to call the parent method inside the subclass? You can use the super keyword

super means to get a reference to the parent class instance. It involves two common usages
In the core volume of Java technology, super is interpreted as a special usage rather than a parent class reference. If it is understood as a parent class reference, it is easier to understand the application of super

1. Use super to construct the constructor of the parent class

 Bird(String name) {
        super(name);
    }

1. Use super to call the normal methods of the parent class

class Bird extends Animal {
    Bird(String name) {
        super(name);
    }

    @Override
    void eat(String food) {
        System.out.println("Bird:eat()" + this.name + food);
        super.eat(food);
    }

    void fly() {
        System.out.println("Bird:fly()" + this.name + "Flying");
    }
}

public static void main(String[] args) {
     Animal animal = new Bird("parrot");
     Bird bird = (Bird) animal;
     bird.eat("food");
 }

Bird:eat()Parrot Food//The eat method of the called Bird subclass
Animal:eat()Parrot Food//Call the eat method of the Animal parent class of [super.eat(food)]

In this code, if eat is called directly in a subclass (without super), the eat method of the subclass will be called by default (that is, overridden), and super is the parent method of the call

Note: the functions of super and this are similar, but there are still some differences

No	difference	this	super
1	concept	Access properties and methods in this class	Subclasses access properties and methods in the parent class
2	Search range	Find this class first. If this class does not, call the parent class	Call the parent class directly without finding this class
3	special	Represents the current object	nothing

11. call the method of rewriting in a construction method (a pit).

class B {
    B() {
        func();
    }

    void func() {
        System.out.println("B.func()");
    }
}

class D extends B {
    private int num = 1;

    D() {
        super();
    }

    @Override
    void func() {
        System.out.println("D.func()" + num);
    }
}

public class TestDemo {

    public static void main(String[] args) {
        D d = new D();
    }
}

View through the javap -c bytecode file command

cxf@cxfdeMacBook-Pro Gao % javap -c TestDemo      
warning: Binary file TestDemo contain bit.basis.Gao.TestDemo
Compiled from "TestDemo.java"
public class bit.basis.Gao.TestDemo {
  public bit.basis.Gao.TestDemo();
    Code:
       0: aload_0
       1: invokespecial #1                  // Method java/lang/Object."<init>":()V
       4: return

  public static void main(java.lang.String[]);
    Code:
       0: new           #2                  // class bit/basis/Gao/D
       3: dup
       4: invokespecial #3                  // Method bit/basis/Gao/D."<init>":()V
       7: astore_1
       8: return
}


Let's see main The assembly code in the function is as follows:
first new An object is described in the following note new Yes D Type object
 Look again invokespecial To see which type of is finally running func Function. The annotation describes D of func That is, the of subclasses func function

After reading it here, analyze the operation process of the code as follows:
D d = new D();
Subclass D Inherit parent class B，and B Construction method of
B The constructor of will trigger dynamic binding and will be called to D of func
 here D It has not been constructed yet, so at this time num Is uninitialized with a value of 0

12. Summary

Polymorphism is a difficult part of object-oriented programming. We will further experience the use of polymorphism in the following abstract classes and interfaces. The focus is on the coding benefits brought by polymorphism

On the other hand, if you put aside Java, polymorphism is actually a broader concept, which is not necessarily related to the syntax of "inheritance"

• The "dynamic polymorphism" in C + + is similar to that in Java. However, C + + also has a "static polymorphism" (template), which has nothing to do with the inheritance system
• Polymorphism in Python embodies "duck type" and has nothing to do with inheritance system
• There is no concept of "inheritance" in Go language, which can also express polymorphism
  No matter what programming language, the core of polymorphism is to let the caller not pay attention to the specific type of object, which is an important way to reduce the user's use cost

2. Abstract class

1. Grammar rules

In the example of printing graphics just now, we found that the draw method in the parent class Shape does not seem to have any actual work. The main drawing graphics are completed by the draw methods of various subclasses of Shape. Like this method without actual work, we can design it as an abstract method. The class containing abstract methods is called abstract class (abstract class).

Before JDK 1.8, the default permission of methods of abstract classes was protected
In JDK 1.8, the default permission of the method of the abstract class is default

abstract class Shape{
	abstract void draw();
}

matters needing attention

1. Abstract classes cannot be instantiated
2. Abstract methods cannot be private
3. Abstract classes can contain other non abstract methods or fields. The rules of this non abstract method are the same as those of ordinary methods. It can be overridden or called directly by subclasses

abstract class Shape{
    abstract void draw();
}
public class TestDemo {

    public static void main(String[] args) {
        Shape shape = new Shape();// Instantiation of abstract classes
    }
}

java: bit.basis.Gao.Shape It's abstract; Cannot instantiate

private abstract class Shape {
    abstract void draw();
}

public class TestDemo {

    public static void main(String[] args) {
    }
}

java: Modifiers are not allowed here private

abstract class Shape {
    abstract void draw();

    void func() {
        System.out.println("Rect: func()");
    }
}

class Rect extends Shape {
    @Override
    void draw() {
        System.out.println("Draw a rectangle");
    }
}

public class TestDemo {
    public static void main(String[] args) {
        Shape shape = new Rect();
        shape.func();
    }
}

Rect: func()

2. Role of abstract classes

Abstract classes exist in order to be inherited

The abstract class itself cannot be instantiated. You must create a subclass of the abstract class, and then you must rewrite the abstract method in the abstract class [quick rewrite: ctrl+o]

Ordinary classes can also be inherited, and ordinary methods can also be rewritten. Why do you have to use abstract classes and abstract methods?

That's true. But using abstract classes is equivalent to a double compiler check
The scenario of using an abstract class is like the above code. The actual work should not be completed by the parent class, but by the child class. At this time, if the parent class is accidentally misused, the ordinary class compiler will not report an error. However, if the parent class is an abstract class, an error will be prompted during instantiation, so that we can find the problem as soon as possible

The meaning of many grammars is to "prevent errors". For example, final, which we have used before, is similar. If the user does not modify the created variables, it is equivalent to constants? But with final, the compiler can remind us in time when we accidentally modify them
Making full use of compiler verification is very meaningful in practical development

3. Interface

1. Grammar rules

Before JDK 1.8, the methods in the interface must be public
In JDK 1.8, the methods in the interface can be public or default
JDK 1.9 is that the method in the interface can be private

An interface is a further step of an abstract class. An abstract class can also contain non abstract methods and fields. While the methods contained in an interface are abstract methods, and fields can only contain
static const

1. Define an interface using interface
2. The methods in the interface must be abstract methods, so abstract can be omitted
3. The methods in the interface must be public, so public can be omitted
4. The implements used by Rect inherits the interface. At this time, the meaning expressed is not "inheritance" but "implementation"
5. When creating, you can also create an interface reference corresponding to an instance of a subclass
6. Similarly, interfaces cannot be instantiated separately
7. The class calling the interface must override the abstract method in the interface [quick rewrite: ctrl+o]

Extensions vs. implementations
Extension refers to the further expansion of functions when certain functions already exist
Implementation means that there is nothing at present and needs to be constructed from scratch

An interface can only contain abstract methods; an interface can only contain static constants

Complete code of method + attribute

public interface IOperation {
public abstract void draw();// void draw();
public static final int a = 10;// int a = 10;
}

The gray part indicates that the code can be omitted

The public, static and final keywords can be omitted. The omitted a still represents the public static constant

1. When we create an interface, the name of the interface usually starts with the capital letter I
2. Interface naming generally uses the word of "adjective"
3. Ali coding specification stipulates that methods and attributes in the interface should not be modified

2. An incorrect code

public interface IOperation {
    void draw();
}

class Circle implements IOperation{
    @Override
    void draw() {
        System.out.println("Draw a circle");
    }
}

Attempting to assign lower access rights; Previously public

Full format

public interface IOperation {
    public abstract void draw();
    public static final int a = 10;
}

Simplified format

public interface IOperation {
    void draw();
    int a = 10;
}

3. Implement multiple interfaces

Sometimes we need to make a class inherit from multiple parent classes at the same time. This is realized by multiple inheritance in some programming languages
However, only single inheritance is supported in Java, and a class can only extend one parent class. However, multiple interfaces can be implemented at the same time, and the similar effect of multiple inheritance can be achieved. Now we represent a group of animals through classes

interface IFlying{
    void flying();
}
interface ISwimming{
    void swimm();
}
interface IRunning{
    void running();
}

class Animal{
    String name = "Animal";

    public Animal(String name) {
        this.name = name;
    }
}

// run
class Cat extends Animal implements IRunning{
    public Cat(String name) {
        super(name);
    }

    @Override
    public void running() {
        System.out.println(this.name + "Cat:running()");
    }
}

// swim
class Fish extends Animal implements ISwimming{
    public Fish(String name) {
        super(name);
    }

    @Override
    public void swimm() {
        System.out.println(this.name + "Fish: swimming()");
    }
}

// Run + swim
class Frog extends Animal implements IRunning, ISwimming{
    public Frog(String name) {
        super(name);
    }

    @Override
    public void swimm() {
        System.out.println(this.name + "Frog: swimming()");
    }

    @Override
    public void running() {
        System.out.println(this.name + "Frog: swimming()");
    }
}

// Run + swim + fly
class Duck extends Animal implements IFlying, IRunning, ISwimming{
    public Duck(String name) {
        super(name);
    }

    @Override
    public void flying() {
        System.out.println(this.name + "Duck: swimming()");
    }

    @Override
    public void swimm() {
        System.out.println(this.name + "Duck: swimming()");
    }

    @Override
    public void running() {
        System.out.println(this.name + "Duck: swimming()");
    }
}

public class TestDemo {
    public static void main(String[] args) {
    }
}

The above code shows the most common usage in Java object-oriented programming: a class inherits a parent class and implements multiple interfaces at the same time. The meaning of inheritance expression is is - a semantics, while the meaning of interface expression is xxx characteristics

A cat is an animal that can run
Frog is also an animal. It can run and swim
Duck is also an animal. It can run, swim and fly

What are the benefits of this design?
Always bear in mind the benefits of polymorphism: forget types. With interfaces, class users don't have to focus on specific types, but only on whether a class has certain capabilities

For example, now implement a method called "walking"

public class TestDemo {
    private static void walk(IRunning running) {
        System.out.println("I took my partner for a walk");
        running.running();
    }

    public static void main(String[] args) {
        Cat cat = new Cat("kitten");
        walk(cat);
        Frog frog = new Frog("Little frog");
        walk(frog);
    }
}

I took my partner for a walk
 kitten Cat:running()
I took my partner for a walk
 Little frog Frog: swimming()

Even the parameter can not be "animal", as long as it can run!

class Robot implements IRunning {
    String name;

    public Robot(String name) {
        this.name = name;
    }

    @Override
    public void running() {
        System.out.println(this.name + "Robot: running()");
    }
}

public class TestDemo {
    public static void main(String[] args) {
        IRunning roboot = new Robot("robot");
        roboot.running();
    }
}

robot Robot: running()

4. Interface usage examples

1.compareable

class Student{
    String name;
    float score;

    public Student(String name, float score) {
        this.name = name;
        this.score = score;
    }

    @Override
    public String toString() {
        return "[" + this.name + ":" + this.score + "]";
    }
}
public class TestDemo {
    public static void main(String[] args) {
        Student[] students = {new Student("A", 1.1f), new Student("D", 4.4f), new Student("C", 3.3f), new Student("B", 2.3f)};
    }
}

According to our previous array, there is a ready-made sort method. Can we call this method directly?

Arrays.sort(students);

Exception in thread "main" java.lang.ClassCastException Student cannot be cast to java.lang.Comparable

After careful consideration, it is not difficult to find that, unlike ordinary integers, two integers can be directly compared, and the size relationship is clear
How to determine the size relationship between two student objects? We need to specify it additionally

Let our Student class implement the Comparable interface and the compareTo method

class Student implements Comparable<Student> {
    String name;
    float score;

    public Student(String name, float score) {
        this.name = name;
        this.score = score;
    }

    @Override
    public String toString() {
        return "[" + this.name + ":" + this.score + "]";
    }

    @Override
    public int compareTo(Student o) {
        return (int) (this.score - o.score);
    }
}

public class TestDemo {
    public static void main(String[] args) {
        Student[] students = {new Student("A", 1.1f), new Student("D", 4.4f), new Student("C", 3.3f), new Student("B", 2.3f)};
        Arrays.sort(students);
        System.out.println(Arrays.toString(students));
    }
}


[[A:1.1], [B:2.3], [C:3.3], [D:4.4]]

Analyze Comparable source code

public interface Comparable: a generic data interface
public int compareTo(T o); an abstract method inside the interface

Therefore, when implementing the Comparable interface, our Student class can fill in the generic data type and rewrite the compareTo method

Return value	meaning
<0	The current object precedes the parameter object
>0	The current object comes after the parameter object
==0	The current object and the parameter object are in no order

In the sort method, the compareTo method will be called automatically. The parameter of compareTo is Object. In fact, what is passed in is an Object of Student type. Then compare the size relationship between the current Object and the parameter Object (calculated by score)

2. comparator [comparator, similar to qsort in C language]

qsort in C language needs to write an additional comparison function. comparator can also realize sorting by writing a function [take bubbling as an example]

public class TestDemo {
    private static void comparable_BubbleSort(){
        Student[] students = {new Student("A", 1.1f), new Student("D", 4.4f), new Student("C", 3.3f), new Student("B", 2.2f)};
        for (int i = 0; i < students.length-1; i++) {
            boolean flg = true;
            for (int j = 0; j < students.length-i-1; j++) {
                if(students[j].compareTo(students[j+1])>0){
                    Student tmp = students[j];
                    students[j] = students[j+1];
                    students[j+1] = tmp;
                    flg = false;
                }
            }
            if (flg){
                break;
            }
        }
        System.out.println(Arrays.toString(students));
    }
    public static void main(String[] args) {
        comparable_BubbleSort();
    }
}

[[A:1.1], [B:2.2], [C:3.3], [D:4.4]]

Careful friends may find that I also rewritten the comparator function in the above code, which is ranked according to scores

@Override
    public int compareTo(Student o) {
        return (int) (this.score - o.score);
    }

With comparable, why is there a comparator?

We found that comparable needs to modify the return value in the data type class, so it is not convenient for subsequent calls. If you want to sort multiple schemes, it is troublesome to modify them every time. Therefore, the comparator was born, which can be used as a "comparator"

In the source code, we know that the returned integer is int: -1, 0, 1. Labels 1, 2 and 3 illustrate the relationship represented by their different values

class ScoreRank implements Comparator<Student> {
    @Override
    public int compare(Student o1, Student o2) {
        return (int) (o1.score-o2.score);
    }
}
class NameRank implements Comparator<Student>{
    @Override
    public int compare(Student o1, Student o2) {
        return o1.name.compareTo(o2.name);
    }
}

    public static void main(String[] args) {
        Student[] students = {new Student("A", 1.1f), new Student("D", 4.4f), new Student("C", 3.3f), new Student("B", 2.2f)};
        Arrays.sort(students, new ScoreRank());
        System.out.println("Score rank: " + Arrays.toString(students));
        Arrays.sort(students, new NameRank());
        System.out.println("Name rank: " + Arrays.toString(students));
    }

Score rank: [[A:1.1], [B:2.2], [C:3.3], [D:4.4]]
Name rank: [[A:1.1], [B:2.2], [C:3.3], [D:4.4]]

We found that the comparator does act as a "comparator". After sorting according to the scheme, you only need to write a class, and then arrays. Sort (data, new class()) can sort the elements of any data type

3. Clonable interface and deep copy

There are many built-in interfaces in Java, and clonable is one of them
There is a clone method in the Object class. Calling this method can realize the "copy" of the Object. However, if you want to call the clone method legally, you must implement the clonable interface. Otherwise, the clonnotsupportedexception error will appear

Error code for interface not implemented:

class Person{
    String name = "abc";
}
public class TestDemo {
    public static void main(String[] args) {
        Person p1 = new Person();
        Person p_clone = (Person) p1.clone();
    }
}

java: clone() stay java.lang.Object Medium is protected access control 

According to the prompt, let's modify the member permissions and have a look

class Person{
    protected String name = "abc";
}
public class TestDemo {
    public static void main(String[] args) {
        Person p1 = new Person();
        Person p_clone = (Person) p1.clone();
    }
}

java: Unreported exception error java.lang.CloneNotSupportedException; It must be captured or declared in order to be thrown

We found that p1.clone() was prompted by the compiler. Let's try exception capture with option+enter

public static void main(String[] args) {
        Person p1 = new Person();
        try {
            Person p_clone = (Person) p1.clone();
            System.out.println("src: " + p1 + "hash: " + p1.hashCode());
            System.out.println("clone: " + p_clone + "hash: " + p_clone.hashCode());
        } catch (CloneNotSupportedException e) {
            e.printStackTrace();
        }
    }

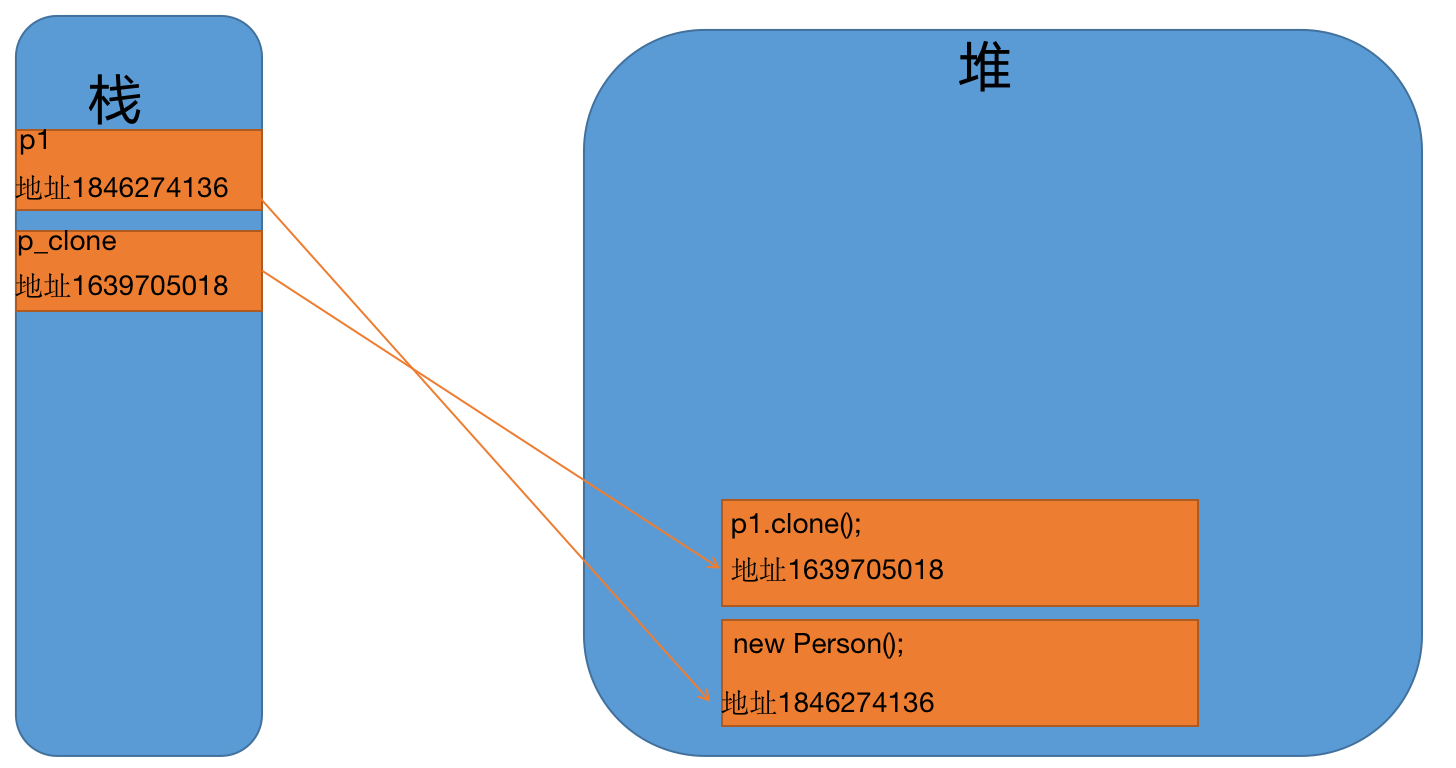
src: Person{name='abc'}hash: 1846274136
clone: Person{name='abc'}hash: 1639705018

The printed hash value is different, indicating that it is a deep copy.

reflection

The appeal code just copies a String type of data. What if it copies an object?
We add an object data element to Person: the Money object
Cloneable copies an object as a "shallow copy"

class Money implements Cloneable{
    protected float money = 12.5f;

    @Override
    protected Object clone() throws CloneNotSupportedException {
        return super.clone();
    }
}
class Person extends Money implements Cloneable {
    protected String name = "abc";
    Money money = new Money();

    @Override
    protected Object clone() throws CloneNotSupportedException {
        return super.clone();
    }

    @Override
    public String toString() {
        return "Person{" +
                "name='" + name + '\'' +
                '}';
    }

}

public class TestDemo {
    public static void main(String[] args) {
        Person p1 = new Person();
        try {
            Person p_clone = (Person) p1.clone();
            System.out.println("p1_hash: " + p1.hashCode() + "; p1_hash_money: " + p1.money.hashCode());
            System.out.println("p_clone_hash: " + p_clone.hashCode() + "; p_clone_hash_money: " + p_clone.money.hashCode());
        } catch (CloneNotSupportedException e) {
            e.printStackTrace();
        }
    }
}

p1_hash: 1846274136; p1_hash_money: 1639705018
p_clone_hash: 1627674070; p_clone_hash_money: 1639705018

We found p1 and P_ If the clone addresses are different, it means that two [deep copies] are copied in memory; The money object has the same address, indicating p1 and P_ Clones share the same address in memory [shallow copy]

How to make deep copy of object data types?

You need to override the clone method in the Person class

1. First clone a copy
2. The money object in the copy is then cloned
3. Finally, return the cloned copy
   Disadvantages: you have to manually write the cloned data every time
   Advantages: enables deep copy

@Override
    protected Object clone() throws CloneNotSupportedException {
        Person personClone = (Person) super.clone();
        personClone.money = (Money) personClone.money().clone();
        return personClone;
    }

The complete code is as follows:

class Money implements Cloneable{
    protected float money = 12.5f;

    @Override
    protected Object clone() throws CloneNotSupportedException {
        return super.clone();
    }
}
class Person extends Money implements Cloneable {
    protected String name = "abc";
    Money money = new Money();

    @Override
    protected Object clone() throws CloneNotSupportedException {
        Person personClone = (Person) super.clone();
        personClone.money = (Money) personClone.money.clone();
        return personClone;
    }

    @Override
    public String toString() {
        return "Person{" +
                "name='" + name + '\'' +
                '}';
    }

}

public class TestDemo {
    public static void main(String[] args) {
        Person p1 = new Person();
        try {
            Person p_clone = (Person) p1.clone();
            System.out.println("p1_hash: " + p1.hashCode() + "; p1_hash_money: " + p1.money.hashCode());
            System.out.println("p_clone_hash: " + p_clone.hashCode() + "; p_clone_hash_money: " + p_clone.money.hashCode());
        } catch (CloneNotSupportedException e) {
            e.printStackTrace();
        }
    }
}

p1_hash: 1846274136; p1_hash_money: 1639705018
p_clone_hash: 1627674070; p_clone_hash_money: 1360875712

At this time, the deep copy is realized, and the address of new Money is also different

5. Inheritance between interfaces

interface IRunning {
    void run();
}

interface ISwimming {
    void swim();
}

// Amphibians can run and swim
interface IAmphibious extends IRunning, ISwimming {

}

class Frog implements IAmphibious {

}

Create a new interface through interface inheritance. IAmphibious means "amphibious". At this time, to implement the Frog class created by the interface, you need to continue to implement the run method and the swim method

Inheritance between interfaces is equivalent to merging multiple interfaces together

6. Summary

Abstract classes and interfaces are common ways to use polymorphism in Java. They both need to be mastered. At the same time, we should recognize the difference between the two
Core difference: abstract classes can contain ordinary methods and fields. Such ordinary methods and fields can be directly used by subclasses (without rewriting), while interfaces cannot contain ordinary methods. Subclasses must override all abstract methods
As in the example of Animal written before, the Animal here contains an attribute such as name, which exists in any subclass. Therefore, the Animal here can only be used as an abstract class, not an interface

class Animal {
    protected String name;
    
	public Animal(String name) {
		this.name = name;
	}
}

Remind again:

The significance of abstract classes is to enable the compiler to better verify. Classes like Animal let us
It will not be used directly, but its subclasses. If you accidentally create an instance of Animal, the compiler will report an error in time to remind us

No	difference	abstract class	Interface
1	Structural composition	Ordinary class + abstract method	Abstract method + global variable
2	jurisdiction	Various permissions	public only
3	Subclass use	extends	implements
4	relationship	An abstract class can implement several interfaces	Interfaces cannot inherit abstract classes, but you can use extensions to extend interface functions
5	Subclass restrictions	A subclass can inherit only one abstract class	A subclass can implement multiple interfaces