1 Preface

The four algorithms are similar, and have the following similarities and differences

2 similarities and differences

Take STR1 = "ABCDEF", STR2 = "zabcdze" as an example

Similarities:

1. Get a target on a string; 2. The core of the algorithm is the idea of dynamic programming.

difference:

1. The targets are different. The maximum common string is the largest continuous subsequence. For example, the maximum common string is "ABCD"  ， The length is 4. The largest common subsequence is "ABCDE", with a length of 5.

2. Edit distance is the minimum number of changes from one string str1 to another string str2. The changes only occur on one string. The changes include three actions: delete, insert and change.

3. Myers may not hear much, but as a programmer, I should have used it. Because diff uses the version comparison algorithm of SVN and GIT, he can comprehensively find the similarities and differences of each node. Although it is dynamic programming, it is different from the traversal mode of the previous three algorithms, which is also essentially different. It will be mentioned here and detailed later. Add that for

No more nonsense. Let's take a direct look at the implementation process of these three.

3 maximum common string (LCS)

The maximum common string is the length of the largest continuous common string. Since it is a dynamic programming, it must be recursive. Write it first.

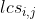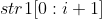Take STR1 = "ABCDEF", STR2 = "zabcdze" as an example,  by  and 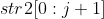 The maximum common string of. Then the recurrence is as follows:

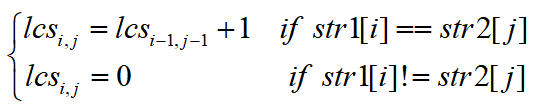
Let's start writing code

def longer_common_string(str1, str2):
    """
    Maximum common string implementation
    """
    len1 = len(str1)
    len2 = len(str2)
    max_lcs_len = 0
    max_len_axis = (0, 0)
    lcs_matrix = [[0 for j in range(len2+1)] for i in range(len1+1)]
    for i, char_1 in enumerate(str1):
        for j, char_2 in enumerate(str2):
            if char_1 == char_2:
                lcs_matrix[i+1][j+1] = lcs_matrix[i][j] + 1
                if lcs_matrix[i+1][j+1] > max_lcs_len:
                    max_lcs_len = lcs_matrix[i+1][j+1]
                    max_len_axis = (i, j)
            else:
                lcs_matrix[i+1][j+1] = 0
    return max_lcs_len, max_len_axis
str1 = "ABCDEF"
str2 = "ZABCDZE"
lcs_len, axis = longer_common_string(str1, str2)
print(lcs_len)
print(axis)

# print result
# 4
# (3, 4)

         The result LCS is obtained_ Len = 4, axis = (3,4), indicating that the maximum common subsequence ends at str1 index 3 and str2 index 4.

4 maximum common subsequence (LCQ)

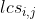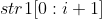        Subsequences can be discontinuous strings, so LCQ > = LCS is always true. For recursive relations, all changes are required,   Take STR1 = "ABCDEF", STR2 = "zabcdze" as an example,  by  and 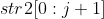 The maximum common string of. Then the recurrence is as follows:

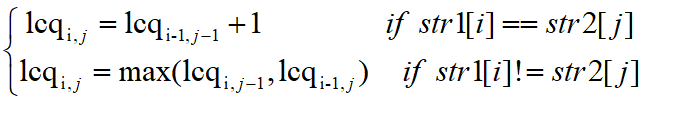
Let's start writing code

def longer_common_sequence(str1, str2):
    """
    Maximum common subsequence implementation
    """
    len1 = len(str1)
    len2 = len(str2)
    max_lcq_len = 0
    max_len_axis = (0, 0)
    lcq_matrix = [[0 for j in range(len2+1)] for i in range(len1+1)]
    for i, char_1 in enumerate(str1):
        for j, char_2 in enumerate(str2):
            if char_1 == char_2:
                lcq_matrix[i+1][j+1] = lcq_matrix[i][j] + 1
                if lcq_matrix[i+1][j+1] > max_lcq_len:
                    max_lcq_len = lcq_matrix[i+1][j+1]
                    max_len_axis = (i, j)
            else:
                lcq_matrix[i+1][j+1] = max(lcq_matrix[i+1][j], lcq_matrix[i][j+1])
    return max_lcq_len, max_len_axis

str1 = "ABCDEF"
str2 = "ZABCDZE"
lcq_len, axis = longer_common_sequence(str1, str2)
print(lcq_len)
print(axis)

# print result
# 5
# (4, 6)

  The meaning of the result is the same as that of LCS and will not be repeated.

5 edit distanceedit distance

        Objective: to make str1 become str2 with the minimum number of operands through three operations: replacement, insertion and deletion

         The difference between editing distance and LCS and LCQ is that editing distance is different. The first two are the same, and in a sense, they have the same goal.

        First the recursive formula, and then explain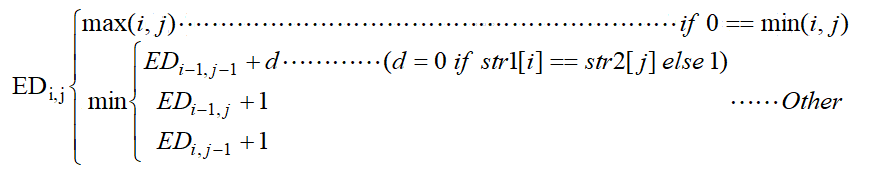

   ED stands for edit distance,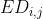express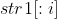and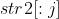Edit distance. Here is a line by line explanation:

 5.1   0==min(i,j)

        Initialization, when i is 0 or j is 0, the editing distance is equal to the maximum value of i and J.

          5.1.1 when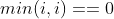, there must be an empty string, assuming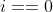, then naturally, from an empty string to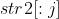need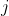Insert operation

5.2   Others

        When i is not equal to 0 and j is not equal to 0, select three operations to replace and delete to complete our goal

       5.2.1 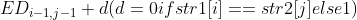Here is the replacement, with   When str2[j] replaces str1[i]. When str1[i]==str2[j], there is no need to replace, so d=0.

        5.2.2 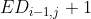 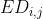， be relative to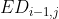There is one more str1[i], and the corresponding operation is delete.

        5.2.2 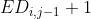 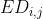，be relative to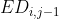, one str2[j] is missing, and the corresponding operation is increase.

      Finally, the minimum value is obtained from the three operations of adding, deleting and inserting.

The code is as follows:

def edit_distance(str1, str2):
    len1 = len(str1)
    len2 = len(str2)
    ed_matrix = [[max(i, j) if 0 == min(i,j) else 0 for j in range(len2+1)] for i in range(len1+1)]
    for i, char_1 in enumerate(str1):
        for j, char_2 in enumerate(str2):
            if char_1 == char_2:
                d = 0
            else:
                d = 1
            replace_dist = ed_matrix[i][j] + d
            insert_dist = ed_matrix[i-1][j] + 1
            delete_dist = ed_matrix[i][j-1] + 1
            ed_matrix[i+1][j+1] = min(replace_dist, insert_dist, delete_dist)
    return ed_matrix[-1][-1]
str1 = "ABCDEF"
str2 = "ZABCDZE"
ed = edit_distance(str1, str2)
print(ed)
# print 
# 3

    Finally, the three bricks above have been thrown away. It's time to lead out the jade

6,Myers

        The above three kinds of dynamic programming take the x and Y axes as the traversal convenience, while Myers traverses in the direction of x+y and x-y. this has the advantage that when encountering continuous str1[i]==str2[j], it can take the fast lane with time complexity of 1.