[small Y learning algorithm] ⚡ Daily LeetCode punch in ⚡ Table 3-39. Preorder traversal of binary tree

📢 preface

🚀 Algorithm problem 🚀

🌲 Punching out an algorithm problem every day is not only a learning process, but also a sharing process 😜
🌲 Tip: the problem-solving programming languages in this column are C# and Java
🌲 To maintain a state of learning every day, let's work together to become the great God of algorithm 🧐!
🌲 Today is the 39th day of punching out the force deduction algorithm 🎈!

🚀 Algorithm problem 🚀

🌲 Example of the original problem: preorder traversal of binary tree

Give you the root node of the binary tree, root, and return the preorder traversal of its node value.

Example 1:

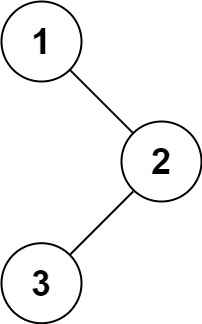
Input: root = [1,null,2,3]
Output:[1,2,3]

Example 2:

Input: root = []
Output:[]

Example 3:

Input: root = [1]
Output:[1]

Example 4:

Input: root = [1,2]
Output:[1,2]

Example 5:

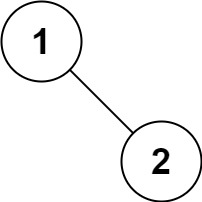
Input: root = [1,null,2]
Output:[1,2]

Tips:

The number of nodes in the tree is in the range [0, 100]
-100 <= Node.val <= 100

🌻 C# method: recursion

Train of thought analysis

The fast and slow pointer starts from the node at the same time. The fast pointer takes two steps at a time and the slow pointer takes one step at a time. If there is a ring, the fast pointer will catch up with the slow pointer sooner or later.

code:

public class Solution 
{
    private IList<int> res = new List<int>();

    public IList<int> PreorderTraversal(TreeNode root) 
    {
        Traversal(root);
        return res;
    }

    private void Traversal(TreeNode node)
    {
        if(node!=null)
        {
            res.Add(node.val);
            PreorderTraversal(node.left);
            PreorderTraversal(node.right);
        }
    }
}

results of enforcement

adopt
 Execution time: 224 ms，At all C# Defeated 70.79% of users in submission
 Memory consumption: 29.8 MB，At all C# Defeated 79.47% of users in submission

🌻 Java method 1: recursion

Train of thought analysis

First of all, we need to understand what is the preorder traversal of a binary tree: we traverse the tree by accessing the root node - left subtree - right subtree, and when accessing the left subtree or right subtree, we traverse in the same way until we traverse the whole tree.

Therefore, the whole traversal process has the nature of recursion. We can directly simulate this process with recursive functions.

Define preorder(root) to represent the answer to the current traversal to the root node. According to the definition, we only need to add the value of the root node to the answer first, then recursively call preorder(root.left) to traverse the left subtree of the root node, and finally recursively call preorder(root.right) to traverse the right subtree of the root node. The condition for recursive termination is that it encounters an empty node.

code:

class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<Integer>();
        preorder(root, res);
        return res;
    }

    public void preorder(TreeNode root, List<Integer> res) {
        if (root == null) {
            return;
        }
        res.add(root.val);
        preorder(root.left, res);
        preorder(root.right, res);
    }
}

results of enforcement

adopt
 Execution time: 0 ms，At all Java  Defeated 100 in submission.00%User
 Memory consumption: 36.6 MB，At all Java Defeated 59 in submission.89%User

Complexity analysis

Time complexity: O( n ),among n Is the number of nodes in the binary tree
 Space complexity: O( n )

🌻 Java method 1: iteration

Train of thought analysis
We can also implement the recursive function of method 1 in an iterative way. The two methods are equivalent. The difference is that a stack is implicitly maintained during recursion,

When iterating, we need to explicitly simulate the stack. The rest of the implementation and details are the same. For details, please refer to the following code

code:

class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<Integer>();
        if (root == null) {
            return res;
        }

        Deque<TreeNode> stack = new LinkedList<TreeNode>();
        TreeNode node = root;
        while (!stack.isEmpty() || node != null) {
            while (node != null) {
                res.add(node.val);
                stack.push(node);
                node = node.left;
            }
            node = stack.pop();
            node = node.right;
        }
        return res;
    }
}

results of enforcement

adopt
 Execution time: 0 ms，At all Java  Defeated 100 in submission.00%User
 Memory consumption: 36.9 MB，At all Java Defeated 5 in submission.45%User

Complexity analysis

Time complexity: O( n ),among n Is the number of nodes in the binary tree
 Space complexity: O( n )

💬 summary

Today is the 39th day of punching out the force deduction algorithm!
This paper uses C# and Java programming languages to solve problems
Some methods are also written by Likou God, and they are also shared while learning. Thanks again to the algorithm bosses
That's the end of today's algorithm sharing. See you tomorrow!

🚀 Previous high-quality article sharing

Posted by Kev on Thu, 23 Sep 2021 07:54:04 -0700

Programmer Group

[small Y learning algorithm] ⚡ Daily LeetCode punch in ⚡ Table 3-39. Preorder traversal of binary tree

📢 preface

🌲 Example of the original problem: preorder traversal of binary tree

🌻 C# method: recursion

🌻 Java method 1: recursion

🌻 Java method 1: iteration

💬 summary

🚀 Previous high-quality article sharing

Hot Keywords