Some time ago, I saw the violent traversal method used by the company's games to realize the shielding word algorithm of the game. Later, I found that the efficiency of this algorithm is relatively low. Therefore, I learned about the trie tree on the Internet, so now I use the trie tree to realize a shielding word algorithm.

Construction principle of trie tree: trie tree is also known as dictionary tree and word lookup tree. The biggest feature is to share the public prefix of string to save space. For example, the trie tree composed of strings "abc" and "abd" is as follows:

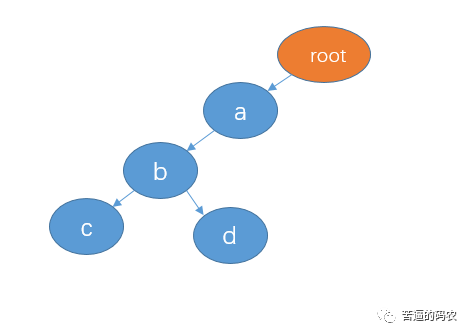
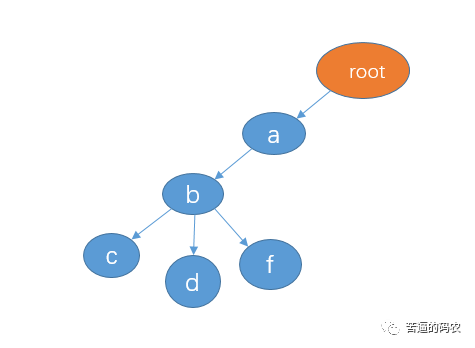
  The root node of the trie tree does not store any data, and each whole branch represents a complete string. abc and abd have a common prefix AB, so we can share node ab. If you insert abf again, it becomes like this:  

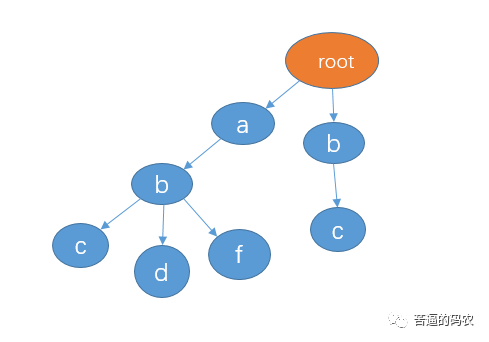
This is true if I insert bc again (bc and the other three strings have no common prefix)

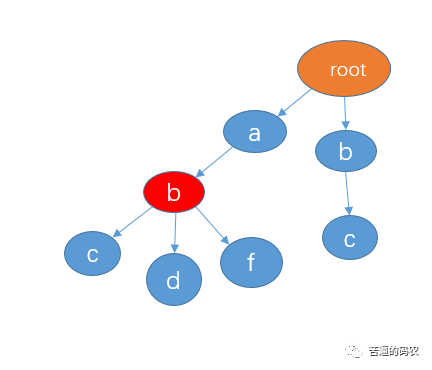
  Each branch may also contain a complete string, so we can make a mark for those nodes that end in a string. For example, ABC, abd and ABF all contain the string ab, so we can make a mark here at node b. As follows (I marked it in red):

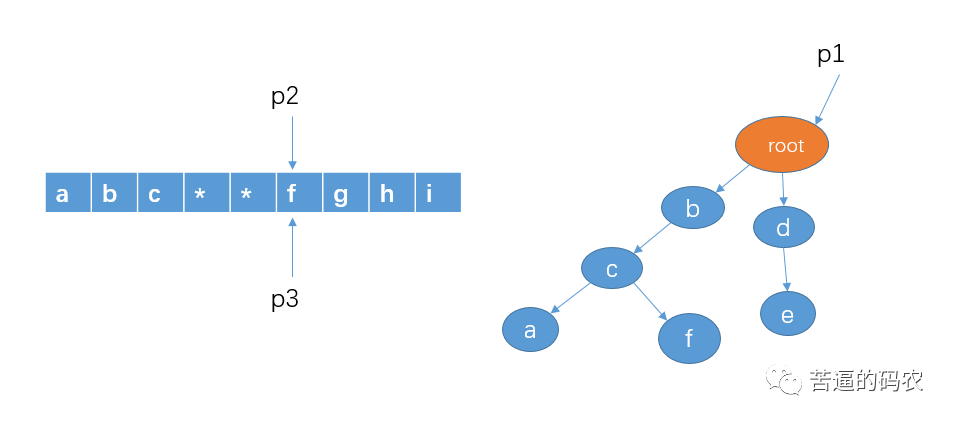
Now let's look at the search principle of trie tree: let's create a trie tree with "de", "BCA" and "BCF", as follows:

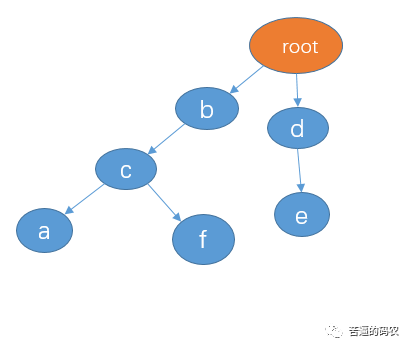
Then we can use three pointers to traverse

1. First, the pointer p1 points to root, and the pointers p2 and p3 point to the first character of the string

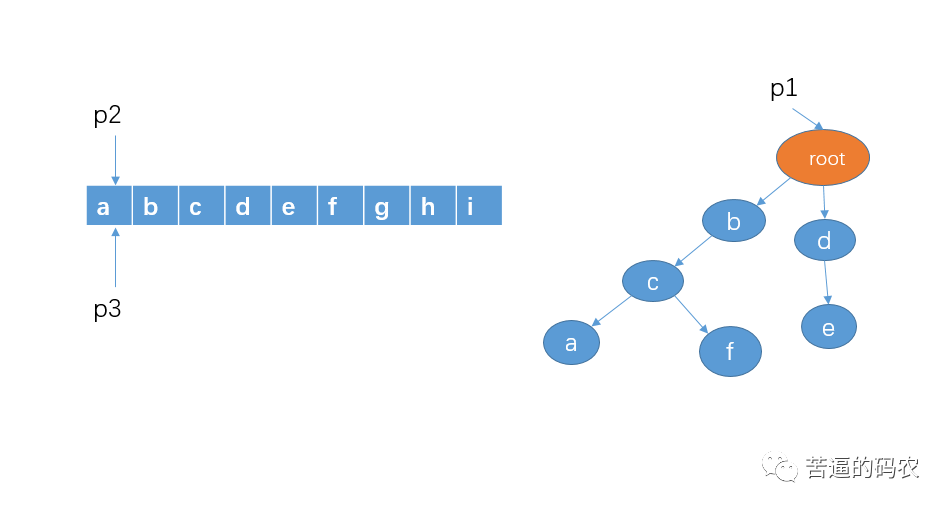
2. Then start with a of the string, detect whether there is a sensitive word prefixed with a, and directly judge whether there is a node in the child node of p1. Obviously, there is no such node. Then move the pointers p2 and p3 one grid to the right.

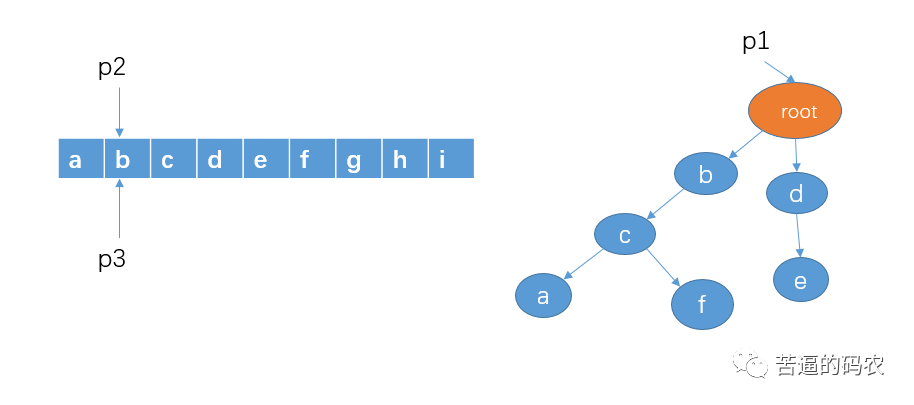
3. Then start searching from the string b to see if there is a string prefixed with b. there is b in the child node of p1. At this time, we point p1 to node b, and p2 moves one grid to the right, but p3 does not move.

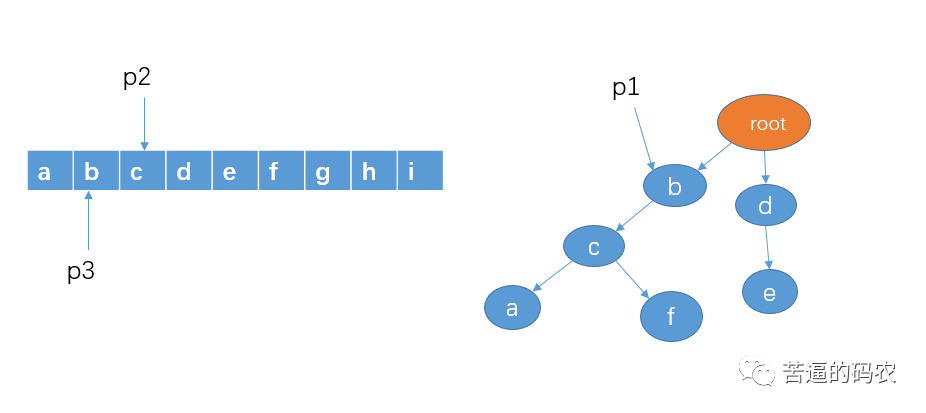
4. It is obvious to judge whether the character c pointed to by p2 exists in the child node of p1. We point p1 to node C, p2 moves one grid to the right, and p3 doesn't move.

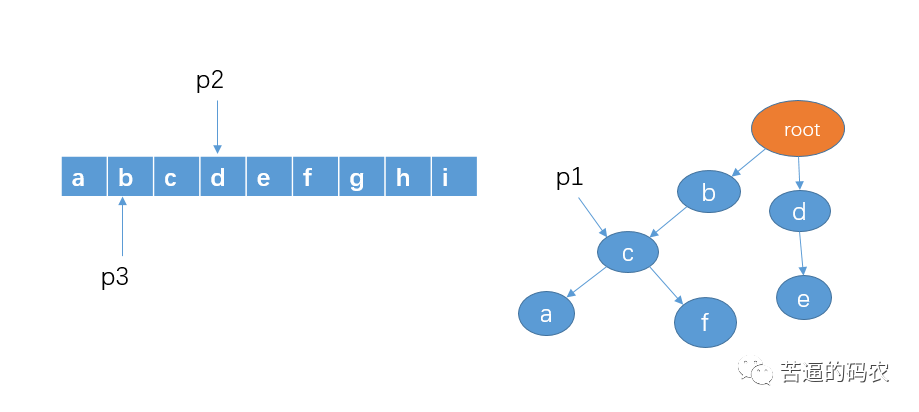
5. Judge whether the character d pointed to by p2 exists in the child node of p1, which is not here. This means that there is no sensitive word prefixed with the character b. At this time, we move p2 and p3 to the character c, and p1 is restored to point to root at the beginning.

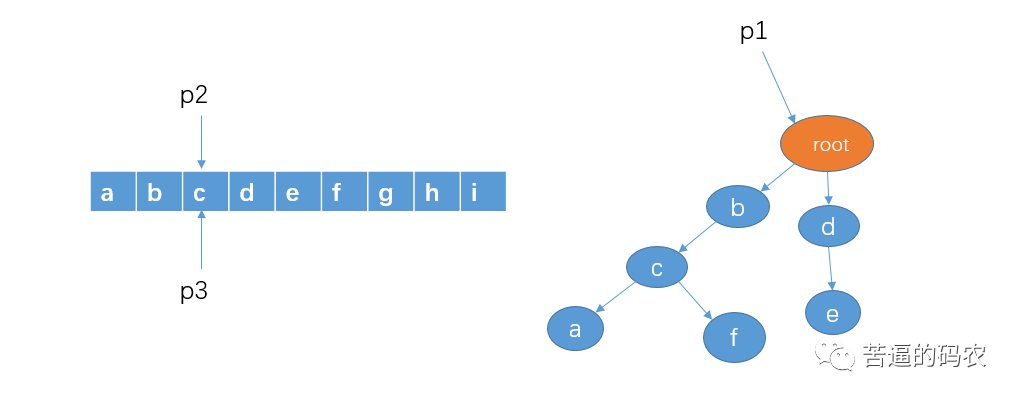
6. As in the previous steps, judge whether there is a string prefixed with c, which is obviously not here, so move p2 and p3 to character d.

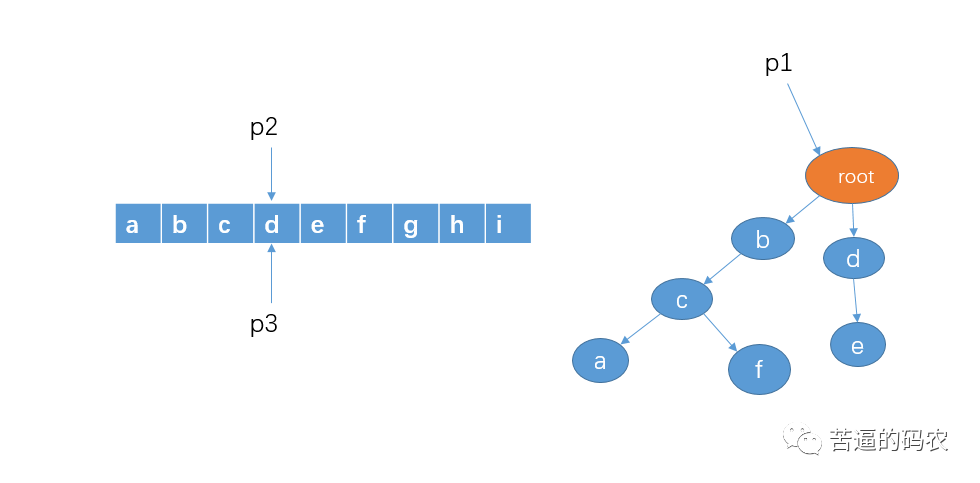
7. Then start from the string D to see if there is a string prefixed with D. there is d in the child node of p1. At this time, we point p1 to node b and move p2 one grid to the right. However, p3 remains the same as before. (see here, I guess you already understand)

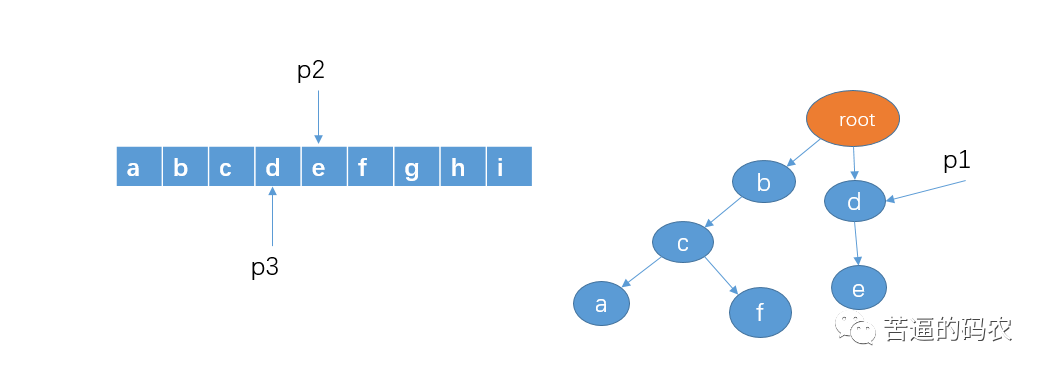
8. It is obvious to judge whether the character e pointed to by p2 exists in the child node of p1. We point p1 to node e, and here e is the last node. The search is over, so there are sensitive words de, that is, p3 and p2. The interval points to sensitive words. Replace those characters in the interval pointed to by p2 and p3 with *. And move p2 and p3 to the character f. As follows:

9. Then repeat the same step until p3 points to the last character.

Complexity analysis

If the length of sensitive words is m, the time complexity of searching for each sensitive word is O(m) and the length of string is n. We need to traverse n times, so the time complexity of searching for sensitive words is O(n * m). If there are t sensitive words, the time complexity of constructing trie tree is O(t * m).

Let me explain here that in practical applications, the time complexity of building a trie tree can be ignored because we can build a trie tree at the beginning and reuse it countless times in the future.

The above is extracted from the article: How to implement the sensitive word filtering algorithm in the game_ trie 

js code implementation:

1: Tree initialization:

    //Pass in the mask word array and estimate the mask word to generate the trie tree
    function makeTree(blockList) {
        wordDic = {};
        let i,len,blockStr,firstChar;
        for(i=0,len=blockList.length;i<len;i++) {
            blockStr = blockList[i];
            firstChar = blockStr[0]
            _makeTree(wordDic,0,blockStr);//Generate trie tree using recursion
            
        }
        return wordDic;
    }

    function _makeTree(dic,i,blockStr) {

        let char = blockStr[i];
        let nextChar = blockStr[i+1];
        if(!dic[char]) dic[char] = {children:{}};
        if(!nextChar) {//Mark this node as the lowest node of a shielded word
            dic[char].isEnd = true
        } else {//Continue to expand this tree
            dic[char].children[nextChar] = _makeTree(dic[char].children,i+1,blockStr)
        }
        return dic[char];
     }

2: Determine whether there is a shielded word

     //Does the input text need deep search
    function hasBlock(inputText,isDeep=false) {
        for(let i=0,len = inputText.length;i<len;i++) {
            let blockStr = _hasBlock(_wordDic,inputText,i,isDeep);
            if(blockStr) return blockStr;
        }
        return null;
    }

    function _hasBlock(dic,inputText,index,isDeep,nowStr="",blockStr=null) {
        let char = inputText[index];//The word has been found and the result is returned
        if(!char) return blockStr;

        let obj = dic[char]//Leaf node returned results found
        if(!obj) return blockStr;

        nowStr += char;
        if(obj.isEnd == true) {
            blockStr = nowStr;
            if(!isDeep) return blockStr;//The first result found is returned directly without deep search
            //Perform a deep search and return the longest result
        }
        return _hasBlock(obj.children,inputText,index+1,isDeep,nowStr,blockStr);
        
    }

3: Make shielded word replacement

    //Returns a masked string of masked word length
    let _replaceStr = ["*","**","***","****","*****","******"];
    function getReplaceStr(len) {
        return _replaceStr[len-1] || "*";
    }

     //Shielded word replacement
    function replace(inputText) {
        let newStr = inputText;
        let blockStr,count;
        for(let i=0,len = inputText.length;i<len;i++) {
            //Use deep traversal to find the longest shielded word
            blockStr = _hasBlock(inputText,i，true);
            if(blockStr) {
                count = blockStr.length;
                newStr = newStr.replace(blockStr,getReplaceStr(count))
                i+=count;
            }

        }
        return newStr;
    }