1 Introduction
1 origin and development of ant colony algorithm (ACA)
In the process of studying the new algorithm, Marco Dorigo and others found that when ant colony is looking for food, they can exchange foraging information by secreting a biological hormone called pheromone, so they can quickly find the target. Therefore, in their doctoral thesis in 1991, they systematically proposed a new intelligent optimization algorithm "Ant system (AS) based on ant population for the first time. Later, The authors and many researchers have made various improvements to the algorithm and applied it to a wider range of fields, such AS graph coloring problem, quadratic assignment problem, workpiece scheduling problem, vehicle routing problem, job shop scheduling problem, network routing problem, large-scale integrated circuit design and so on. In recent years, M.Dorigo et al. Further developed ant algorithm into a general optimization technology "Ant Colony Optimization (ACO)", and called all algorithms conforming to ACO framework "ACO algorithm".
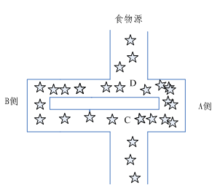
Specifically, each ant starts looking for food without telling where the food is in advance. When one finds food, it will release a volatile secretion pheromone (called pheromone, which will gradually volatilize and disappear over time, and the pheromone concentration represents the distance of the path) to the environment. Pheromone can be perceived by other ants and play a guiding role. Usually, when there are pheromones on multiple paths, ants will preferentially choose the path with high pheromone concentration, so that the pheromone concentration of the path with high concentration is higher, forming a positive feedback. Some ants don't always repeat the same path as other ants. They will find another way. If the other path is shorter than the original path, gradually, more ants are attracted to this shorter path. Finally, after a period of operation, the shortest path may be repeated by most ants. Finally, the path with the highest pheromone concentration is the optimal path finally selected by ants.
Compared with other algorithms, ant colony algorithm is a relatively young algorithm, which has the characteristics of distributed computing, no central control, asynchronous and indirect communication between individuals, and is easy to be combined with other optimization algorithms. After the continuous exploration of many people with lofty ideals, a variety of improved ant colony algorithms have been developed today, but the principle of ant colony algorithm is still the backbone.
2. Solution principle of ant colony algorithm
Based on the above description of ant colony foraging behavior, the algorithm mainly simulates the foraging behavior in the following aspects:
(1) The simulated graph scene contains two pheromones, one represents home and the other represents the location of food, and both pheromones are volatilizing at a certain rate.
(2) Each ant can only perceive information in a small part of its surroundings. When ants are looking for food, if they are within the perceptual range, they can go directly. If they are not within the perceptual range, they have to go to the place with more pheromones. Ants can have a small probability not to go to the place with more pheromones and find another way. This small probability event is very important, represents a way finding innovation, and is very important to find a better solution.
(3) The rules for ants to return to their nest are the same as those for finding food.
(4) When moving, ants will first follow the guidance of pheromones. If there is no guidance of pheromones, they will go inertia according to their moving direction, but there is also a certain chance to change the direction. Ants can also remember the road they have traveled and avoid going to a place repeatedly.
(5) Ants leave the most pheromones when they find food, and then the farther away from the food, the less pheromones they leave. The rules for finding the amount of pheromone left in the nest are the same as those of food. Ant colony algorithm has the following characteristics: positive feedback algorithm, concurrency algorithm, strong robustness, probabilistic global search, independent of strict mathematical properties, long search time and easy to stop.
Ant transfer probability formula: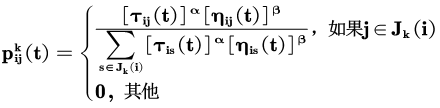
In the formula: is the probability of ant k transferring from city i to j; α,β The relative importance of pheromones and heuristic factors; Is the pheromone quantity on edge (i,j); Is heuristic factor; Select the city allowed for the ant k next step. The above formula is the pheromone update formula in ant system, which is the pheromone quantity on edge (i,j); ρ Is the pheromone evaporation coefficient, 0< ρ< 1. Is the pheromone quantity left by the kth ant on the edge (i,j) in this iteration; Q is a normal coefficient; is the path length of the kth ant in this tour.
In the ant system, the pheromone update formula is: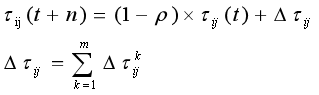
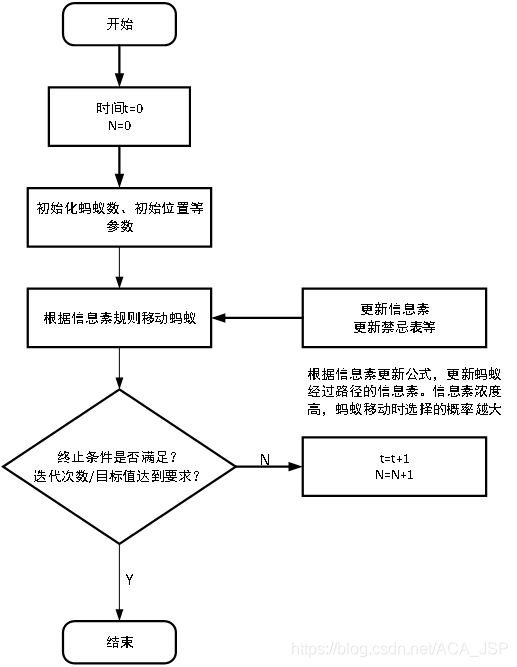
3 solution steps of ant colony algorithm:
(1) Initialization parameters at the beginning of calculation, relevant parameters need to be initialized, such as ant colony size (number of ants) m and pheromone importance factor α, Heuristic function importance factor β, Pheromone will send silver ρ, Total pheromone release Q, maximum number of iterations iter_max, initial value of number of iterations iter=1.
(2) The solution space is constructed. Each ant is randomly placed at different starting points. For each ant K (k=1,2,3... m), the next city to be visited is calculated according to (2-1) until all ants have visited all cities.
(3) Update the information Su, calculate the path length Lk(k=1,2,..., m) of each ant, and record the optimal solution (shortest path) in the current number of iterations. At the same time, update the pheromone concentration on the connection path of each city according to equations (2-2) and (2-3).
(4) Judge whether to terminate. If ITER < iter_max, make iter=iter+1, clear the record table of ant passing path, and return to step 2; otherwise, terminate the calculation and output the optimal solution.
(5) Judge whether to terminate. If ITER < iter_max, make iter=iter+1, clear the record table of ant passing path and return to step 2; otherwise, terminate the calculation and output the optimal solution. 3. Judge whether to terminate. If ITER < iter_max, make iter=iter+1, clear the record table of ant passing path and return to step 2; otherwise, terminate the calculation and output the optimal solution.
Part 2 source code
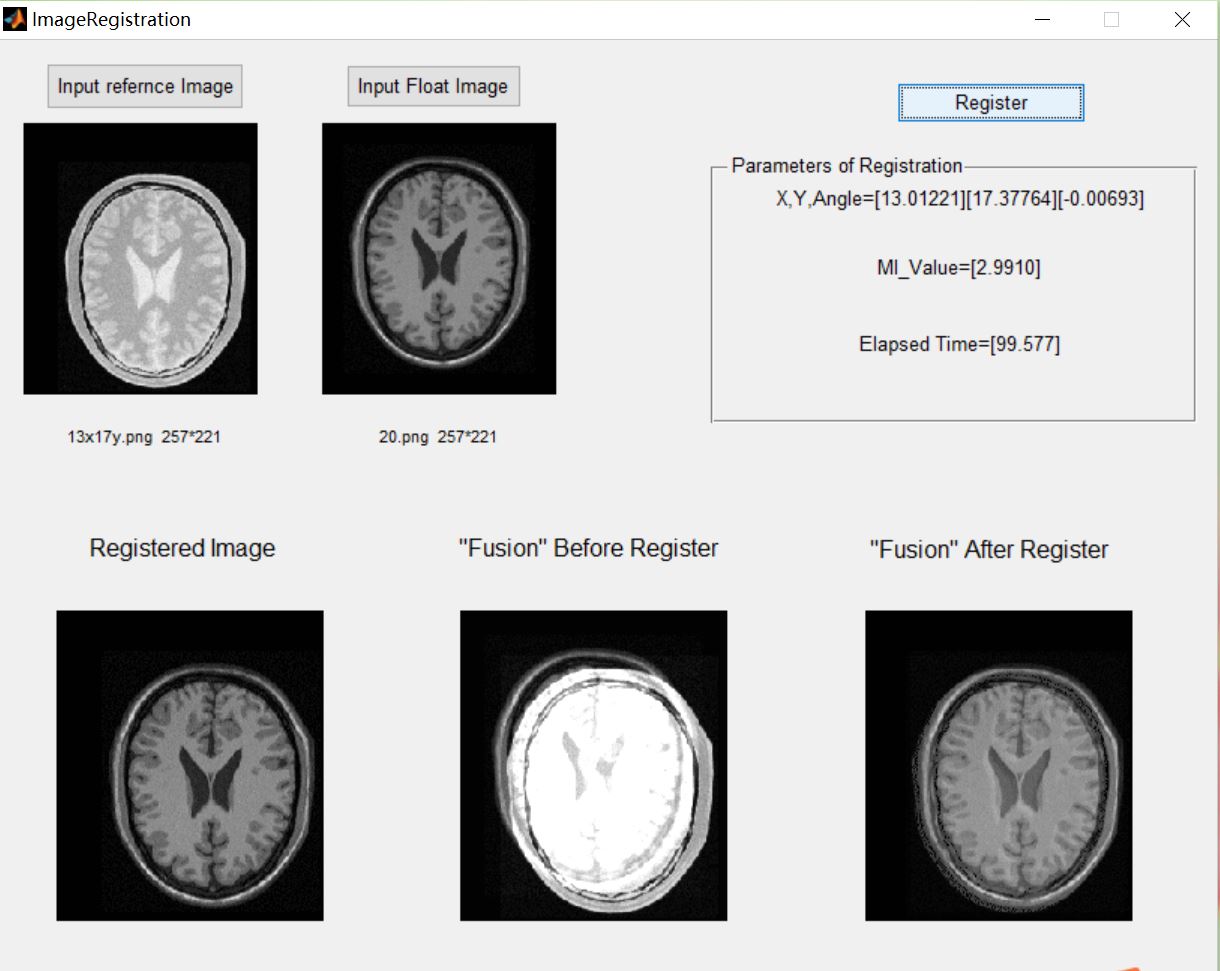
function varargout = ImageRegistration(varargin)
% IMAGEREGISTRATION M-file for ImageRegistration.fig
% IMAGEREGISTRATION, by itself, creates a new IMAGEREGISTRATION or raises the existing
% singleton*.
%
% H = IMAGEREGISTRATION returns the handle to a new IMAGEREGISTRATION or the handle to
% the existing singleton*.
%
% IMAGEREGISTRATION('CALLBACK',hObject,eventData,handles,...) calls the local
% function named CALLBACK in IMAGEREGISTRATION.M with the given input arguments.
%
% IMAGEREGISTRATION('Property','Value',...) creates a new IMAGEREGISTRATION or raises the
% existing singleton*. Starting from the left, property value pairs are
% applied to the GUI before ImageRegistration_OpeningFcn gets called. An
% unrecognized property name or invalid value makes property
% application
% stop. All inputs are passed to ImageRegistration_OpeningFcn via varargin.
%
% *See GUI Options on GUIDE's Tools menu. Choose "GUI allows only one
% instance to run (singleton)".
%
% See also: GUIDE, GUIDATA, GUIHANDLES
% Edit the above text to modify the response to help ImageRegistration
% Last Modified by GUIDE v2.5 24-May-2021 17:01:50
% Begin initialization code - DO NOT EDIT
gui_Singleton = 1;
gui_State = struct('gui_Name', mfilename, ...
'gui_Singleton', gui_Singleton, ...
'gui_OpeningFcn', @ImageRegistration_OpeningFcn, ...
'gui_OutputFcn', @ImageRegistration_OutputFcn, ...
'gui_LayoutFcn', [] , ...
'gui_Callback', []);
if nargin && ischar(varargin{1})
gui_State.gui_Callback = str2func(varargin{1});
end
if nargout
[varargout{1:nargout}] = gui_mainfcn(gui_State, varargin{:});
else
gui_mainfcn(gui_State, varargin{:});
end
% End initialization code - DO NOT EDIT
addpath(pwd);
% --- Executes just before ImageRegistration is made visible.
function ImageRegistration_OpeningFcn(hObject, eventdata, handles, varargin)
% This function has no output args, see OutputFcn.
% hObject handle to figure
% eventdata reserved - to be defined in a future version of MATLAB
% handles structure with handles and user data (see GUIDATA)
% varargin command line arguments to ImageRegistration (see VARARGIN)
% Choose default command line output for ImageRegistration
handles.output = hObject;
% Update handles structure
guidata(hObject, handles);
% UIWAIT makes ImageRegistration wait for user response (see UIRESUME)
% uiwait(handles.figure1);
% --- Outputs from this function are returned to the command line.
function varargout = ImageRegistration_OutputFcn(hObject, eventdata, handles)
% varargout cell array for returning output args (see VARARGOUT);
% hObject handle to figure
% eventdata reserved - to be defined in a future version of MATLAB
% handles structure with handles and user data (see GUIDATA)
% Get default command line output from handles structure
varargout{1} = handles.output;
% --- Executes on button press in pushbutton1.
function pushbutton1_Callback(hObject, eventdata, handles)
% hObject handle to pushbutton1 (see GCBO)
% eventdata reserved - to be defined in a future version of MATLAB
% handles structure with handles and user data (see GUIDATA)
clc
%%%%%%%%%%%%%%%call OpenImage.m Read in the reference image and obtain the file name and image size%%%%%%%%%%%%
[fname,pname,index]=uigetfile({'*.jpg;*.bmp;*.png;*.tif;*.gif;*.jpeg'},'Select reference image');
if index
name=[pname fname];
temp=imread(name);
[m,n]=size(temp);
m=num2str(m);
n=num2str(n);
imsize=[' ',m,'*',n];
handles.ImsizeI=imsize;
handles.filenameI=name;
handles.names_dispI=[fname,imsize];
end
set(handles.text2,'String',handles.names_dispI);
guidata(hObject,handles);
%%%%%%%%%%%%%%%%%%Display reference image%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
axes(handles.axes1)
I=imread(handles.filenameI);
save I;
imshow(I)
figure(5)
imshow(I)
% --- Executes on button press in pushbutton2.
function pushbutton2_Callback(hObject, eventdata, handles)
% hObject handle to pushbutton2 (see GCBO)
% eventdata reserved - to be defined in a future version of MATLAB
% handles structure with handles and user data (see GUIDATA)
clc
%%%%%%%%%%%call OpenImage.m Read in the floating image and obtain the file name and image size%%%%%%%%%%
[fname,pname,index]=uigetfile({'*.jpg;*.bmp;*.png;*.tif;*.gif;*.jpeg'},'Select floating image');
if index
name=[pname fname];
temp=imread(name);
[m,n]=size(temp);
m=num2str(m);
n=num2str(n);
imsize=[' ',m,'*',n];
handles.ImsizeJ=imsize;
handles.filenameJ=name;
handles.names_dispJ=[fname,imsize];
end
set(handles.text3,'String',handles.names_dispJ);
guidata(hObject,handles);
%%%%%%%%%%%%%%%%%%Display floating image%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
axes(handles.axes2)
J=imread(handles.filenameJ);
imshow(J)
figure(6)
imshow(J)
% --- Executes on button press in pushbutton3.
function pushbutton3_Callback(hObject, eventdata, handles)
% hObject handle to pushbutton3 (see GCBO)
% eventdata reserved - to be defined in a future version of MATLAB
% handles structure with handles and user data (see GUIDATA)
clc
%%%%%%%%%%%%%%%%Detect whether the reference image and floating image have been input%%%%%%%%%%%%%%%%%%%%%%%%%%
axesIbox=get(handles.axes1,'box');
axesJbox=get(handles.axes2,'box');
if strcmp(axesIbox,'off')||strcmp(axesJbox,'off')
errordlg('Please select Image for Registration','Error')
error('NO Image!')
end
%%%%%%%%%%%%%%%Detect whether the size of the reference image is the same as that of the floating image%%%%%%%%%%%%%%%%%%%%%%%%%
handles.isSameSizeIJ=strcmp(handles.ImsizeI,handles.ImsizeJ);
if handles.isSameSizeIJ~=1
errordlg('Please select the Same Size Image','Error')
error('Image Size doesn"t match!')
end
%%%%%%%%%%%%%Read and copy images, one for registration process and the other for output after registration%%%%%%%%%
I1=imread(handles.filenameI);
J1=imread(handles.filenameJ);
handles.Old_I=I1;
handles.Old_J=J1;
I=I1;
J=J1;
handles.I=I;
handles.J=J;
guidata(hObject,handles);
%%%%%%%%%%%%%Displays the "fusion" of the pre registration reference image and the floating image"design sketch%%%%%%%%%%%%%%%%%%%%
axes(handles.axes4)
imshow(uint8(I+J))
%%%%%%%%%%%%%%%Call function GLPF.m(Gaussian low pass filter),Complete Gaussian low-pass preprocessing%%%%%%%%%%%%%
[I,J]=GLPF(handles);
handles.I=I;
handles.J=J;
guidata(hObject,handles);
%%%%%%%%%%%%%%Call function Powell.m,Image registration%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
tic
RegistrationParameters=Powell(handles);
%RegistrationParameters=AntColony(handles);
%RegistrationParameters=AntColonyimprove(handles);
toc
ElapsedTime=toc;
%%%%%%%%%%%%%%Display registration results%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
handles.RegistrationParameters=RegistrationParameters;
y=RegistrationParameters(1);
x=RegistrationParameters(2);
ang=RegistrationParameters(3);
RegistrationResult=sprintf('X,Y,Angle=[%.5f][%.5f][%.5f]',x,y,ang);
MI_Value=RegistrationParameters(4);
MI_Value=sprintf('MI_Value=[%.4f]',MI_Value);
ElapsedTime=sprintf('Elapsed Time=[%.3f]',ElapsedTime);
axes(handles.axes5)
[FusionImage,RegistrationImage]=Fusion(handles);
imshow(FusionImage)
axes(handles.axes3)
imshow(RegistrationImage)
figure(7)
imshow(RegistrationImage)
set(handles.text8,'string',RegistrationResult);
set(handles.text9,'string',MI_Value);
set(handles.text10,'string',ElapsedTime);
3 operation results