General idea of the topic

Main idea of the title:

Problem solving ideas:

1. First, we must find the shortest path between any two points → F l o y e d \rightarrow Floyed → Floyed shortest path algorithm
2. Now let's assume that only two points are fixed x , y x,y x. Y to solve the answer.
3. The first thing we found was x x x and y y There must be the shortest circuit between y. what if there are multiple shortest circuits?
   
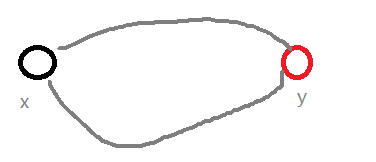
4. There must be no answer!! Because there is at most one path on the tree, but for the points on the other path, it must not be optimal, because you y y y has to go through x x x. Or x x x goes through y y y to the point in the link, it must not be the shortest path, so there are multiple shortest paths, and the answer must be 0
5. about x x x and y y The point above the y path must have only one choice d [ x ] [ v ] + d [ v ] [ y ] = d [ x ] [ y ] d[x][v]+d[v][y]=d[x][y] d[x][v]+d[v][y]=d[x][y]
6. If not x x x and y y How to solve the point above the y path?
7. First of all, I thought so at first d [ x ] [ v ] = d [ x ] [ y ] + d [ y ] [ v ]    or    d [ y ] [ v ] = d [ y ] [ x ] + d [ x ] [ v ] d[x][v]=d[x][y]+d[y][v]\;\text{or}\;d[y][v]=d[y][x]+d[x][v] d[x][v]=d[x][y]+d[y][v]ord[y][v]=d[y][x]+d[x][v], but this formula does not reflect the path?
8. If a path is determined by two points, we are introducing an additional point v ′ v' v′
9. Then the formula becomes d [ x ] [ v ] = d [ x ] [ v ′ ] + 1 & & d [ y ] [ v ] = d [ y ] [ v ′ ] + 1 d[x][v]=d[x][v']+1\&\&d[y][v]=d[y][v']+1 d[x][v]=d[x][v′]+1&&d[y][v]=d[y][v′]+1
10. We know that the shortest path tree is from each point to x x x and y y y is the shortest, if we fix it x x When x is the root, the hierarchy of the tree where each point is located will be fixed

11. Different trees are linked in different ways between each layer
12. Let's look at the above enumeration v ′ v' v ′ sum v v v is just the point between two adjacent layers.
13. Because each point is linked independently, we have a clear understanding of each point v v v we can enumerate the points around it to see how many points there are v ′ v' v 'satisfies the above formula, assuming that c u r v cur_v curv​. Then we multiply by the principle of multiplication
14. a n s x , y = ∏ c u r v ans_{x,y}=\prod_{} cur_v ansx,y​=∏​curv​

AC code

O ( n 2 ∗ m ) O(n^2*m) O(n2∗m)

#include <bits/stdc++.h>
#define mid ((l + r) >> 1)
#define Lson rt << 1, l , mid
#define Rson rt << 1|1, mid + 1, r
#define ms(a,al) memset(a,al,sizeof(a))
#define log2(a) log(a)/log(2)
#define lowbit(x) ((-x) & x)
#define IOS std::ios::sync_with_stdio(0); cin.tie(0); cout.tie(0)
#define INF 0x3f3f3f3f
#define LLF 0x3f3f3f3f3f3f3f3f
#define f first
#define s second
#define endl '\n'
using namespace std;
const int N = 2e6 + 10, mod = 998244353;
const int maxn = 500010;
const long double eps = 1e-5;
const int EPS = 500 * 500;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int,int> PII;
typedef pair<ll,ll> PLL;
typedef pair<double,double> PDD;
template<typename T> void read(T &x) {
   x = 0;char ch = getchar();ll f = 1;
   while(!isdigit(ch)){if(ch == '-')f*=-1;ch=getchar();}
   while(isdigit(ch)){x = x*10+ch-48;ch=getchar();}x*=f;
}
template<typename T, typename... Args> void read(T &first, Args& ... args) {
   read(first);
   read(args...);
}
vector<int> G[500];
int d[500][500], ans[500][500];
int n, m;
inline void init() {
	for(int i = 1; i <= n; ++ i) d[i][i] = 0;
	for(int i = 1; i <= n; ++ i)
	   for(int j = 1; j <= n; ++ j)
	     for(int k = 1; k <= n; ++ k)
		   d[j][k] = min(d[j][k],d[j][i]+d[i][k]);
}
int main() {
	IOS;
	ms(d,INF);
	cin >> n >> m;
	for(int i = 1; i <= m; ++ i) {
		int u, v;
		cin >> u >> v;
		G[u].push_back(v);
		G[v].push_back(u);
		d[u][v] = d[v][u] = 1;
	}
	init();
    for(int i = 1; i <= n; ++ i)
	    for(int j = i; j <= n; ++ j) {
			bool ok = true;
            vector<int>pos(d[i][j] + 1,-1);
            for(int k = 1;k <= n;k++) {
                if(d[i][k] + d[k][j] == d[i][j]) {
                    if(pos[d[i][k]] != -1) {
                        ok = false;
						break;
                    }
                    pos[d[i][k]] = k;
                }
            }
            if(!ok) continue;
            int cur = 1;
            for(int k = 1;k <= n;k++) {
                if(d[i][k] + d[k][j] > d[i][j]) {
                    int cnt = 0; //Represents the number of edges that can reach point k in bfs tree
                    for(int e = 0;e < G[k].size();e++) {
                        int v = G[k][e];
                        if(d[i][v] + 1 == d[i][k] && d[j][v] + 1 == d[j][k]) cnt++;
                        
                    }
                    cur = 1ll * cur * cnt % mod;
                }
            }
            ans[i][j] = ans[j][i] = cur;
		}	
	for(int i = 1;i <= n;i++) {
        for(int j = 1;j <= n;j++) {
            printf("%d ",ans[i][j]);
        }
        printf("\n");
    }
	return 0;
}