Flexible job shop scheduling has been studied before. The research is summarized as follows: Code implementation of solving flexible job shop scheduling problem based on Genetic Algorithm in python (including detailed description of standard example quasi transformation, coding, decoding, crossover and mutation) Using python to solve the dual resource constrained flexible job shop scheduling problem with preparation time based on ant colony algorithm
Today, let's talk about the HFSP problem and give the corresponding code implementation.
1 problem description
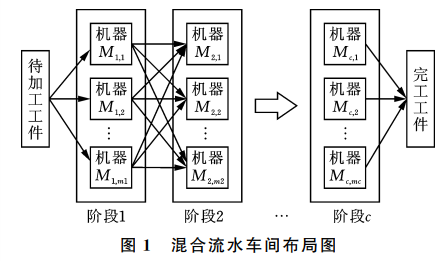
Hybrid flow shop (also known as flexible flow shop) introduces multiple selectable parallel machines in all or part stages on the basis of flow shop, which improves the productivity and flexibility of the workshop. It is one of the research hotspots in the field of job shop scheduling. The HFSP problem can be described as: n workpieces are processed continuously in (C ≥ 2) stages, there are mi(mi ≥ 1; i = 1,2,..., c) machines in stage i, and there are multiple machines in at least one stage. HFSP needs to optimize one or more performance indexes according to the processing sequence and machine allocation of workpieces in each stage. Figure 1 shows the layout of HFSP workshop
Differences between HFSP and other issues:
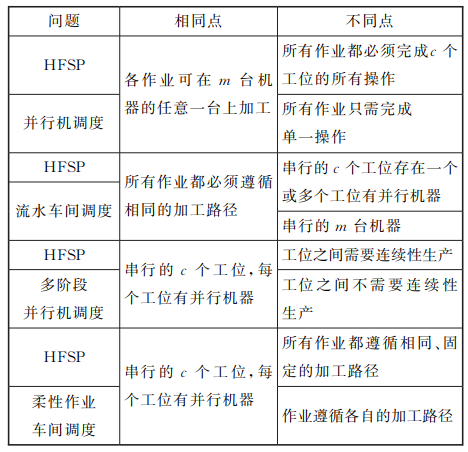
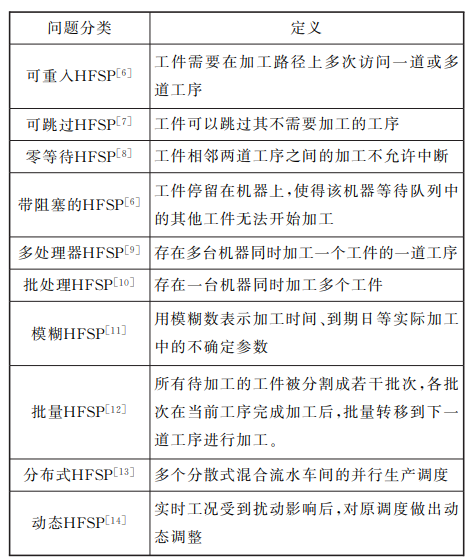
Expand the classification and definition of HFSP:
Common objective functions of HFSP:
(1) Completion time
(2) Flow time
(3) Workpiece delay
(4) Workload
(5) Total energy consumption
... ...
The objective function of this paper is to minimize the completion time
2 algorithm
Genetic algorithm is very good for getting started. Almost all other similar evolutionary algorithms evolve on this basis. When you understand the logic and ideas of genetic algorithm, you can start other algorithms quickly. Therefore, this paper still decides to use genetic algorithm to solve them.
2.1 initialization
2.1.1 coding
At present, most algorithms for solving HFSP adopt the coding method based on workpiece arrangement, that is, the workpieces are arranged in a sequential queue, and the position of the workpieces in the queue indicates the processing sequence of the first process of the workpieces. Since the processing of workpieces in the subsequent stage is greatly affected by the previous stage, this method is also adopted. The subsequent stage is coded in non descending order according to the processing completion time of workpieces in the previous stage. For example, the code of five workpieces is (4, 2, 5, 1, 3). This code indicates that in the first processing stage, workpiece 4 is processed first, followed by workpiece 2, followed by 5, then 1, and finally workpiece 3. If they are processed in the first stage and reach the second stage in the order of 2, 5, 4, 1 and 3, the coding in the second stage is (2, 5, 4, 1 and 3), and the coding in subsequent stages is the same.
2.1.2 decoding
For the above coding method, a scheduling scheme can be constructed by using the following decoding algorithm:
Step 1 Calculate the start time, completion time, processing time and current machine load of the current operation for all available machines of each operation of each workpiece. When calculating the start time of an operation, it is necessary to compare the completion time (TP) of the last operation of the workpiece with the completion time (TM) of the last operation processed by the machine. If TM ≥ TP, and there is a gap between TP and TM on the machine greater than the processing time of the process, the process can be inserted into the gap, and the start time is the end time of the previous process in the gap; If TM < TP, the start time is TP.
Step 2 Select the machine. The optimization principle is: give priority to the machine with the least completion time; If the completion time is the same, select the machine with the lowest load of the current machine; If the machine loads are the same, select the machine at random. That is, the priority is completion time > machine load.
Step 3 Judge whether all processes of all workpieces have been machine selected. If it is selected, the cycle is ended and the scheduling scheme is output; Otherwise, return to step 1
Crossover mode: POX
Variation: disrupt interchange
3 code
3.1 Instance
import random
random.seed(32)
#State: stage, i.e. how many operations does the workpiece have? Job: number of workpieces, Machine['type':list], corresponding to the number of parallel machines in each stage
def Generate(State,Job,Machine):
PT=[]
for i in range(State):
Si=[] #Stage i processing
for j in range(Machine[i]):
S0=[random.randint(1,20) for k in range(Job)]
Si.append(S0)
PT.append(Si)
return PT
Job=20
State=5
Machine=[3,3,2,3,3]
PT=Generate(State,Job,Machine)3.2 Scheduling
import random
import matplotlib.pyplot as plt
from Instance import Job,State,Machine,PT
import numpy as np
class Item:
def __init__(self):
self.start=[]
self.end=[]
self._on=[]
self.T=[]
self.last_ot=0
self.L=0
def update(self,s,e,on,t):
self.start.append(s)
self.end.append(e)
self._on.append(on)
self.T.append(t)
self.last_ot=e
self.L+=t
class Scheduling:
def __init__(self,J_num,Machine,State,PT):
self.M=Machine
self.J_num=J_num
self.State=State
self.PT=PT
self.Create_Job()
self.Create_Machine()
self.fitness=0
def Create_Job(self):
self.Jobs=[]
for i in range(self.J_num):
J=Item()
self.Jobs.append(J)
def Create_Machine(self):
self.Machines=[]
for i in range(len(self.M)): #Highlight the stages of machines, that is, which machines are in each stage
State_i=[]
for j in range(self.M[i]):
M=Item()
State_i.append(M)
self.Machines.append(State_i)
#Decoding at each stage
def Stage_Decode(self,CHS,Stage):
for i in CHS:
last_od=self.Jobs[i].last_ot
last_Md=[self.Machines[Stage][M_i].last_ot for M_i in range(self.M[Stage])] #Machine completion time
last_ML = [self.Machines[Stage][M_i].L for M_i in range(self.M[Stage])] #Machine load
M_time=[self.PT[Stage][M_i][i] for M_i in range(self.M[Stage])] #Processing time of the machine for the current operation
O_et=[last_Md[_]+M_time[_] for _ in range(self.M[Stage])]
if O_et.count(min(O_et))>1 and last_ML.count(last_ML)>1:
Machine=random.randint(0,self.M[Stage])
elif O_et.count(min(O_et))>1 and last_ML.count(last_ML)<1:
Machine=last_ML.index(min(last_ML))
else:
Machine=O_et.index(min(O_et))
s, e, t=max(last_od,last_Md[Machine]),max(last_od,last_Md[Machine])+M_time[Machine],M_time[Machine]
self.Jobs[i].update(s, e,Machine, t)
self.Machines[Stage][Machine].update(s, e,i, t)
if e>self.fitness:
self.fitness=e
#decode
def Decode(self,CHS):
for i in range(self.State):
self.Stage_Decode(CHS,i)
Job_end=[self.Jobs[i].last_ot for i in range(self.J_num)]
CHS = sorted(range(len(Job_end)), key=lambda k: Job_end[k], reverse=False)
#Draw a Gantt chart
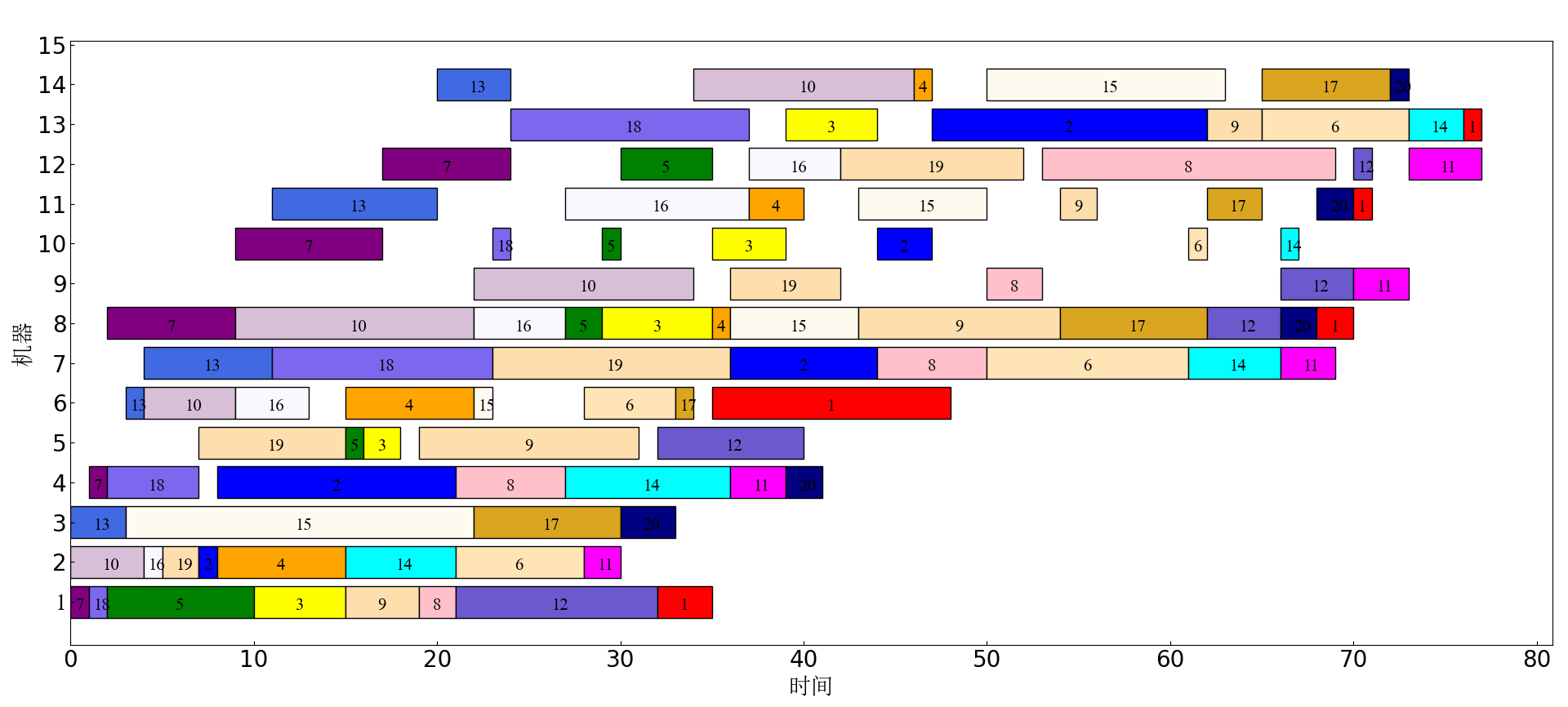
def Gantt(self):
fig = plt.figure()
M = ['red', 'blue', 'yellow', 'orange', 'green', 'moccasin', 'purple', 'pink', 'navajowhite', 'Thistle',
'Magenta', 'SlateBlue', 'RoyalBlue', 'Aqua', 'floralwhite', 'ghostwhite', 'goldenrod', 'mediumslateblue',
'navajowhite','navy', 'sandybrown']
M_num=0
for i in range(len(self.M)):
for j in range(self.M[i]):
for k in range(len(self.Machines[i][j].start)):
Start_time=self.Machines[i][j].start[k]
End_time=self.Machines[i][j].end[k]
Job=self.Machines[i][j]._on[k]
plt.barh(M_num, width=End_time - Start_time, height=0.8, left=Start_time, \
color=M[Job], edgecolor='black')
plt.text(x=Start_time + ((End_time - Start_time) / 2 - 0.25), y=M_num - 0.2,
s=Job+1, size=15, fontproperties='Times New Roman')
M_num += 1
plt.yticks(np.arange(M_num + 1), np.arange(1, M_num + 2), size=20, fontproperties='Times New Roman')
plt.ylabel("machine", size=20, fontproperties='SimSun')
plt.xlabel("time", size=20, fontproperties='SimSun')
plt.tick_params(labelsize=20)
plt.tick_params(direction='in')
plt.show()
#
# Sch=Scheduling(J_num,Machine,State,PT)
3.3 GA
import random
import numpy as np
import copy
from Scheduling import Scheduling as Sch
from Instance import Job,State,Machine,PT
import matplotlib.pyplot as plt
class GA:
def __init__(self,J_num,State,Machine,PT):
self.State=State
self.Machine=Machine
self.PT=PT
self.J_num=J_num
self.Pm=0.2
self.Pc=0.9
self.Pop_size=100
# Randomly generated chromosome
def RCH(self):
Chromo = [i for i in range(self.J_num)]
random.shuffle(Chromo)
return Chromo
# Generate initial population
def CHS(self):
CHS = []
for i in range(self.Pop_size):
CHS.append(self.RCH())
return CHS
#choice
def Select(self, Fit_value):
Fit = []
for i in range(len(Fit_value)):
fit = 1 / Fit_value[i]
Fit.append(fit)
Fit = np.array(Fit)
idx = np.random.choice(np.arange(len(Fit_value)), size=len(Fit_value), replace=True,
p=(Fit) / (Fit.sum()))
return idx
# overlapping
def Crossover(self, CHS1, CHS2):
T_r = [j for j in range(self.J_num)]
r = random.randint(2, self.J_num) # An integer r is generated in the interval [1,T0]
random.shuffle(T_r)
R = T_r[0:r] # Generate r unequal integers according to the random number r
# Copy the chromosomes of the parents into the offspring and maintain their order and position
H1=[CHS1[_] for _ in R]
H2=[CHS2[_] for _ in R]
C1=[_ for _ in CHS1 if _ not in H2]
C2=[_ for _ in CHS2 if _ not in H1]
CHS1,CHS2=[],[]
k,m=0,0
for i in range(self.J_num):
if i not in R:
CHS1.append(C1[k])
CHS2.append(C2[k])
k+=1
else:
CHS1.append(H2[m])
CHS2.append(H1[m])
m+=1
return CHS1, CHS2
# variation
def Mutation(self, CHS):
Tr = [i_num for i_num in range(self.J_num)]
# Machine selection section
r = random.randint(1, self.J_num) # Select r positions in the mutant chromosome
random.shuffle(Tr)
T_r = Tr[0:r]
K=[]
for i in T_r:
K.append(CHS[i])
random.shuffle(K)
k=0
for i in T_r:
CHS[i]=K[k]
k+=1
return CHS
def main(self):
BF=[]
x=[_ for _ in range(self.Pop_size+1)]
C=self.CHS()
Fit=[]
for C_i in C:
s=Sch(self.J_num,self.Machine,self.State,self.PT)
s.Decode(C_i)
Fit.append(s.fitness)
best_C = None
best_fit=min(Fit)
BF.append(best_fit)
for i in range(self.Pop_size):
C_id=self.Select(Fit)
C=[C[_] for _ in C_id]
for Ci in range(len(C)):
if random.random()<self.Pc:
_C=[C[Ci]]
CHS1,CHS2=self.Crossover(C[Ci],random.choice(C))
_C.extend([CHS1,CHS2])
Fi=[]
for ic in _C:
s = Sch(self.J_num, self.Machine, self.State, self.PT)
s.Decode(ic)
Fi.append(s.fitness)
C[Ci]=_C[Fi.index(min(Fi))]
Fit.append(min(Fi))
elif random.random()<self.Pm:
CHS1=self.Mutation(C[Ci])
C[Ci]=CHS1
Fit = []
Sc=[]
for C_i in C:
s = Sch(self.J_num, self.Machine, self.State, self.PT)
s.Decode(C_i)
Sc.append(s)
Fit.append(s.fitness)
if min(Fit)<best_fit:
best_fit=min(Fit)
best_C=Sc[Fit.index(min(Fit))]
BF.append(best_fit)
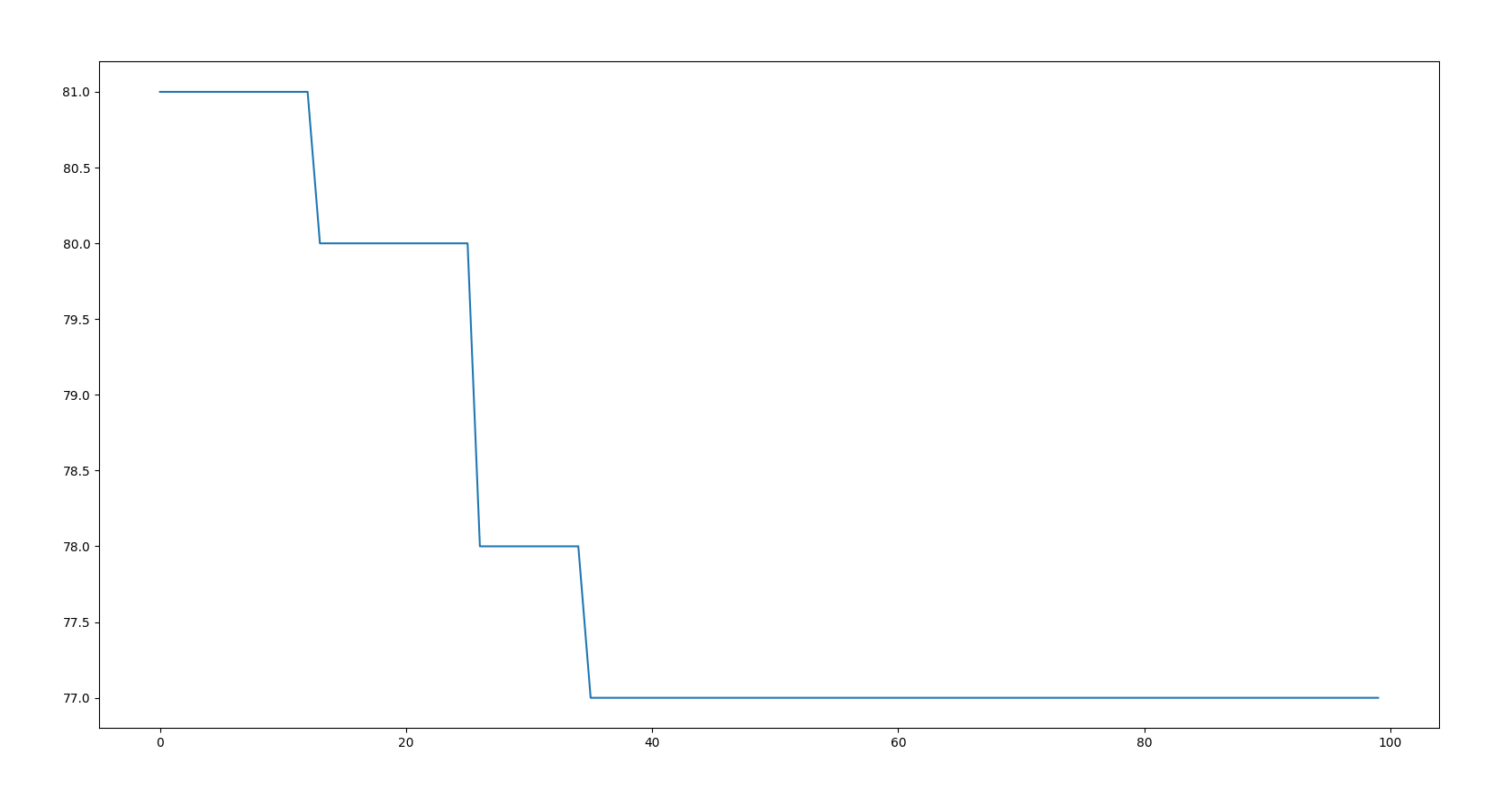
plt.plot(x,BF)
plt.show()
best_C.Gantt()
if __name__=="__main__":
g=GA(Job,State,Machine,PT)
g.main()
4 experimental results