Pytorch machine learning (VIII) -- NMS non maximum suppression and DIOU-NMS improvement in yoov5

preface

In the prediction stage of target detection, many candidate anchor box es will be output, many of which are obviously overlapping prediction bounding boxes, all around the same target. At this time, I can use NMS to merge similar bounding boxes of the same target, or retain the best of these bounding boxes.

If you don't understand IOU and other knowledge, you can see my last blog Pytorch machine learning (V) -- loss function in target detection (l2, IOU, GIOU, DIOU, CIOU)

1, NMS non maximum suppression algorithm

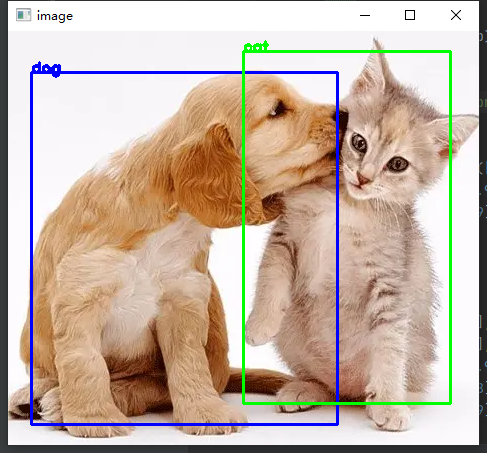
Let's take a look at the visual understanding of NMS. The left figure shows the bbox of two ground truth s, and the right figure shows the prediction box of my own analog network output.

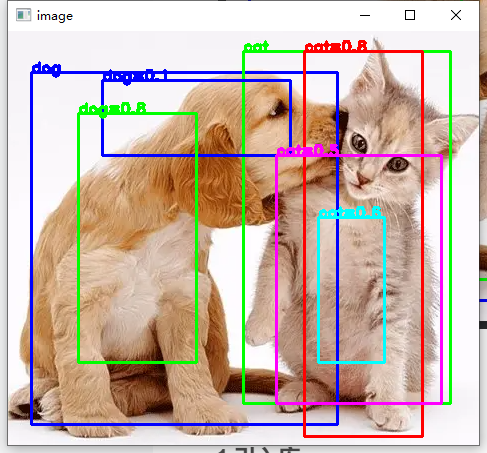
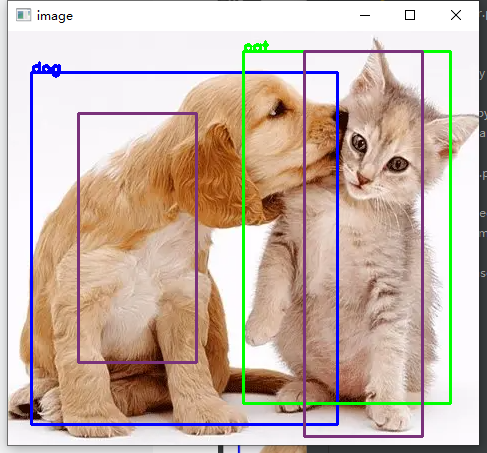
  The following figure shows the non maximum suppression I realized using the NMS officially provided by pytoch. It can be seen that the prediction frame retains the best effect and removes the redundant prediction frame after NMS.

 

  Let's talk about the flow of NMS algorithm, which is actually very simple

         1, Select the prediction bounding box B1 with the highest confidence from all candidate boxes as the benchmark, and then remove all other bounding boxes whose IOU with B1 exceeds the predetermined threshold.

(at this time, B1 is the highest confidence bounding box among all bounding boxes, and there is no bounding box too similar to it - the bounding box with non maximum confidence is suppressed)

         2, Select the bounding box B2 with the second highest confidence from all candidate boxes as a benchmark, and remove all other bounding boxes whose IOU with B2 exceeds the predetermined threshold.

        3, Repeat the above operation until all prediction boxes are used as benchmarks - at this time, no pair of bounding boxes are too similar

2, Hard NMS non maximum code

In the source code of YOLOV5, the author directly calls the official NMS API of pytoch

Non in general.py_ max_ In the suppression function

"""
among boxes by Nx4 of tensor，N Is the number of boxes, 4 is x1 y1 x2 y2
socres by N Dimensional tensor，Represents the confidence of each box
iou_thres Is in the above algorithm IOU threshold
 The return value is a list arranged in descending order according to the confidence after removing the too similar box, and we can output the prediction box according to this list
"""
i = torchvision.ops.nms(boxes, scores, iou_thres)  # NMS

In order to facilitate the subsequent improvement of other NMS, we also write an NMS algorithm ourselves, which draws lessons from Mu Shen's code b station link , you can directly change the torchvision.ops.nms above to the NMS function below in YOLOV5

def NMS(boxes, scores, iou_thres, GIoU=False, DIoU=False, CIoU=False):
    """

    :param boxes:  (Tensor[N, 4])): are expected to be in ``(x1, y1, x2, y2)
    :param scores: (Tensor[N]): scores for each one of the boxes
    :param iou_thres: discards all overlapping boxes with IoU > iou_threshold
    :return:keep (Tensor): int64 tensor with the indices
            of the elements that have been kept
            by NMS, sorted in decreasing order of scores
    """
    # Sort by conf from large to small
    B = torch.argsort(scores, dim=-1, descending=True)
    keep = []
    while B.numel() > 0:
        # Take out the one with the highest confidence
        index = B[0]
        keep.append(index)
        if B.numel() == 1: break
        # To calculate iou, you can select giou, Diou and ciou as required
        iou = bbox_iou(boxes[index, :], boxes[B[1:], :], GIoU=GIoU, DIoU=DIoU, CIoU=CIoU)
        # Found subscripts that match the threshold
        inds = torch.nonzero(iou <= iou_thres).reshape(-1)
        B = B[inds + 1]
    return torch.tensor(keep)

Here is the function for calculating IOU - bbox_iou directly refers to the code in yoov5, which succinctly integrates the calculation of giou, Diou and ciou.

def bbox_iou(box1, box2, x1y1x2y2=True, GIoU=False, DIoU=False, CIoU=False, eps=1e-9):
    # Returns the IoU of box1 to box2. box1 is 4, box2 is nx4
    box2 = box2.T

    # Get the coordinates of bounding boxes
    if x1y1x2y2:  # x1, y1, x2, y2 = box1
        b1_x1, b1_y1, b1_x2, b1_y2 = box1[0], box1[1], box1[2], box1[3]
        b2_x1, b2_y1, b2_x2, b2_y2 = box2[0], box2[1], box2[2], box2[3]
    else:  # transform from xywh to xyxy
        b1_x1, b1_x2 = box1[0] - box1[2] / 2, box1[0] + box1[2] / 2
        b1_y1, b1_y2 = box1[1] - box1[3] / 2, box1[1] + box1[3] / 2
        b2_x1, b2_x2 = box2[0] - box2[2] / 2, box2[0] + box2[2] / 2
        b2_y1, b2_y2 = box2[1] - box2[3] / 2, box2[1] + box2[3] / 2

    # Intersection area
    inter = (torch.min(b1_x2, b2_x2) - torch.max(b1_x1, b2_x1)).clamp(0) * \
            (torch.min(b1_y2, b2_y2) - torch.max(b1_y1, b2_y1)).clamp(0)

    # Union Area
    w1, h1 = b1_x2 - b1_x1, b1_y2 - b1_y1 + eps
    w2, h2 = b2_x2 - b2_x1, b2_y2 - b2_y1 + eps
    union = w1 * h1 + w2 * h2 - inter + eps

    iou = inter / union
    if GIoU or DIoU or CIoU:
        cw = torch.max(b1_x2, b2_x2) - torch.min(b1_x1, b2_x1)  # convex (smallest enclosing box) width
        ch = torch.max(b1_y2, b2_y2) - torch.min(b1_y1, b2_y1)  # convex height
        if CIoU or DIoU:  # Distance or Complete IoU https://arxiv.org/abs/1911.08287v1
            c2 = cw ** 2 + ch ** 2 + eps  # convex diagonal squared
            rho2 = ((b2_x1 + b2_x2 - b1_x1 - b1_x2) ** 2 +
                    (b2_y1 + b2_y2 - b1_y1 - b1_y2) ** 2) / 4  # center distance squared
            if DIoU:
                return iou - rho2 / c2  # DIoU
            elif CIoU:  # https://github.com/Zzh-tju/DIoU-SSD-pytorch/blob/master/utils/box/box_utils.py#L47
                v = (4 / math.pi ** 2) * torch.pow(torch.atan(w2 / h2) - torch.atan(w1 / h1), 2)
                with torch.no_grad():
                    alpha = v / ((1 + eps) - iou + v)
                return iou - (rho2 / c2 + v * alpha)  # CIoU
        else:  # GIoU https://arxiv.org/pdf/1902.09630.pdf
            c_area = cw * ch + eps  # convex area
            return iou - (c_area - union) / c_area  # GIoU
    else:
        return iou  # IoU

3, DIOU-NMS

In fact, DIOU-NMS is to change the IOU threshold in the NMS algorithm I mentioned above to DIOU, and set DIOU in the NMS code to True.

According to DIOU's paper, if NMS is simply used, that is, IOU is used as the threshold to screen out other prediction frames, when two objects are too close, it is likely that the prediction frame of the other object will be filtered out.

Like the motorcycle in the picture below. Using DIOU-NMS can improve the detection of close objects to a certain extent.

  4, Soft NMS

There is also a soft NMS algorithm on the Internet. Its idea is the traditional NMS. If other boxes are directly removed only through the IOU value, it may be inappropriate, so soft NMS is introduced.

The specific process is that we change the NMS algorithm from removing other bounding boxes to modifying the confidence of other bounding boxes.

Here is a picture of a blogger

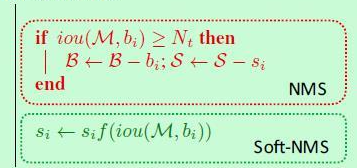
  The f () function is now a Gaussian function

si is the confidence, M is the bounding box of the current maximum confidence, and bi is other bounding boxes

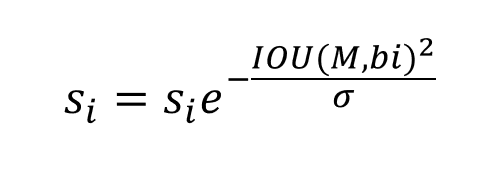
Online views on this effect are also mixed. I haven't tried it myself, but intuitively, I personally don't think the effect will be greatly improved. If you are interested, you can try it yourself.