Red black tree test connection
234 tree test link
What are the advantages of red and black trees
The query performance of the red black tree is slightly inferior to that of the AVL tree, because the red black tree is slightly unbalanced compared with the AVL tree, resulting in one more layer, that is, the query performance of the red black tree is only compared once more than that of the AVL tree with the same content. However, the red black tree can basically destroy the AVL tree in terms of insertion and deletion. Each insertion and deletion of the AVL tree will carry out a large number of balance calculations. For the red black tree, the overhead of red black transformation and rotation operations according to maintaining the red black property is much smaller than that of the AVL tree
Mapping relationship between red black tree and 234 tree
What is 234B
234 tree features:
- Strict balanced tree
- There are no child nodes or only the corresponding number of child nodes on each node
- The number of layers of the tree corresponding to each leaf node is certain
- Follow the principle of upward growth
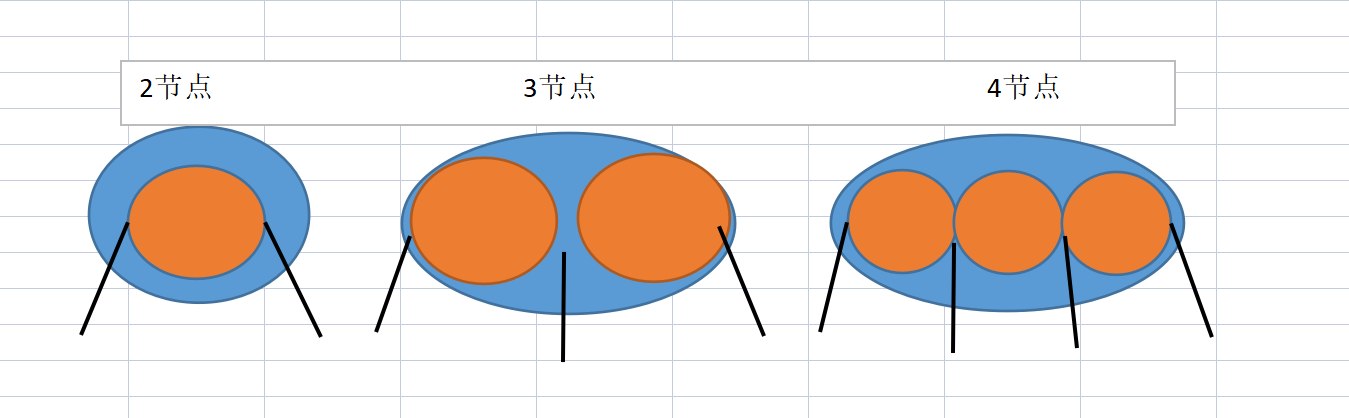
234 node correspondence
Each blue chassis is a node of a 234 tree, and each orange in each node is an element in a node. When filling 234 tree, either there is no child node or each black line in the node is filled with child nodes, otherwise the B-tree balance is not satisfied
234 tree growth
- When you add an element, you will find the appropriate location and place it on the appropriate node
- If there are four elements (5-node type) in the node after adding this element, the element in the middle of the three elements in the original node should be raised as the parent node, and the left and right elements of the original node should be taken as the left and right child nodes of the parent node respectively
- For the combination of the parent node mentioned above and the parent node element of the original node, if there are four elements after the combination, repeat step 2

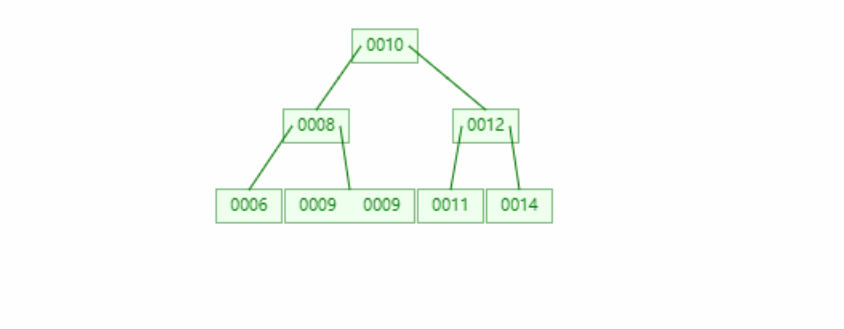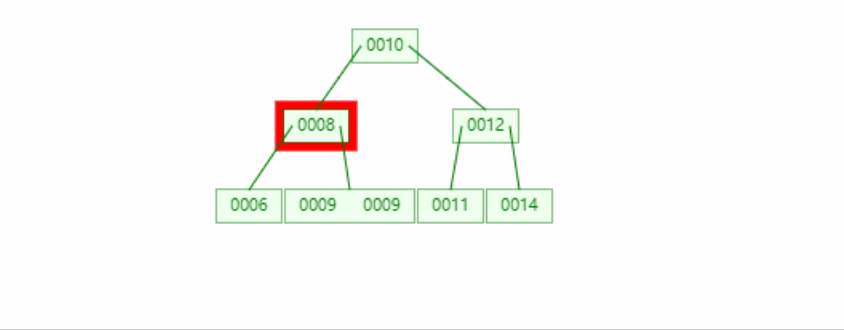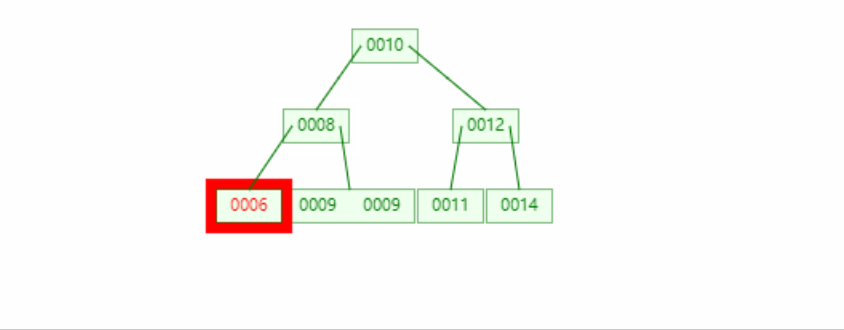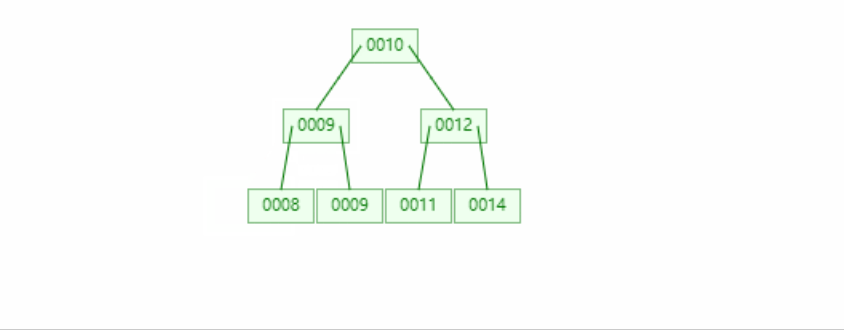
234 deletion of tree
-
Deleting a specified element in a node does not change the structure of the tree. It will be deleted directly without other operations (step 1 in the figure below)

-
If deleting a specified node will affect the node balance, it will borrow from the node of the nearest redundant node, but not directly, but indirectly through the parent node
-
If there is no node to borrow in the whole tree, the balance of input and output will be maintained by reducing the number of layers

Mapping relationship

- A red black tree only corresponds to a 234 tree, and a 234 tree may correspond to multiple red black trees.
- The red nodes of the red black tree cannot be continuous
- The node in a 234 tree corresponds to only one black node in the red black tree. Therefore, the number of black nodes in the leaf node path from any node in the red black tree to this node must be the same
Convert Test
This is a colored 234 tree:

Convert to red and black: (the label indicates that there are several black nodes on the path)

Properties of red black tree
- Nodes are red and black
- The root node is black
These two can be understood as the definition of red black tree
- All leaves are black
There may be some questions about this. In fact, when dealing with the node of the red black tree, if the node is a leaf node, two black empty nodes will be filled in the back, which is only omitted in the above example.

- There are two black nodes under the left and right red nodes
Article 3 is only valid when intervening
- The number of black nodes on the simple path from any node to all leaf nodes of this node must be certain (black balance)
According to the balance of 234 tree, each node has and only has one black node corresponding to the node of red black tree
Note: black nodes on the path cannot include empty black nodes
Node classes and basic methods
public class RBTree<K extends Comparable<K>,V>{
private RBNode root;//Define the root node first
private static final boolean BLACK=true;//Black is true
private static final boolean RED=false;//Red is false
//Get node color
private static boolean getColor(RBNode rbNode){
//It is black when the node is empty because the last layer is black
//This can avoid null pointers in subsequent complex processing
return rbNode==null?BLACK:rbNode.color;
}
//Set node color
private static void setColor(RBNode rbNode, boolean b){
if(rbNode!=null){
rbNode.color=b;
}
}
//Get parent node
private static RBNode parentOf(RBNode rbNode){
return rbNode==null?null:rbNode.parent;
}
//Get left child node
private static RBNode leftOf(RBNode rbNode){
return rbNode==null?null:rbNode.left;
}
//Get right child node
private static RBNode rightOf(RBNode rbNode){
return rbNode==null?null:rbNode.right;
}
//The node class is placed in the RBTree class as an inner class
//The generic K-key value of this class (the key in TreeMap) inherits the Comparable interface for subsequent comparison
static class RBNode<K extends Comparable<K>,V>{
K key;
V value;
private boolean color;
RBTree.RBNode parent;//Parent node
RBTree.RBNode left;//Left node
RBTree.RBNode right;//Right node
//Create constructor
public RBNode(K key, V value, RBTree.RBNode parent) {
this.key = key;
this.value = value;
this.color = BLACK;
this.parent = parent;
}
//You can display the value of the key value pair when calling the preamble traversal
@Override
public String toString() {
return "RBNode{" +
"key=" + key +
", value=" + value +
", color=" + (color?"BLACK":"RED") +
'}';
}
//Some get set methods
public RBTree.RBNode getLeft() {
return left;
}
public RBTree.RBNode getRight() {
return right;
}
public boolean isColor() {
return color;
}
public V getValue() {
return value;
}
}
}
The reason why there are these private methods is that in the subsequent process, whether it is left-right rotation or node color judgment, it will not worry about null pointer exceptions.
Left and right rotation of red and black trees
Left-handed Figure 1
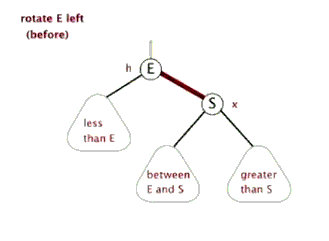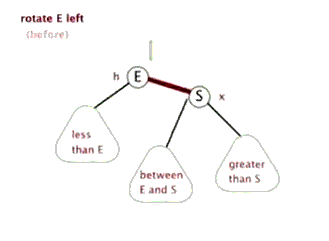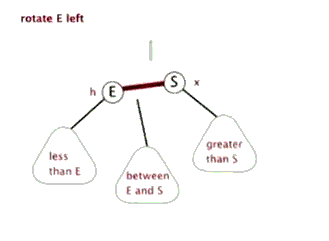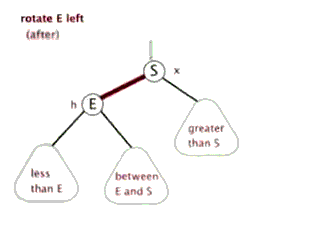
Left handed Figure 2
- The p node is the left rotation of the p node
- The blue arrow is the parent node of the subtree
- The green node is the node at the color position, which may be empty
- l is the node used to replace p

- Color P to l and set p to red

- Change the point of the parent node and give the left subtree of l to the right tree of p
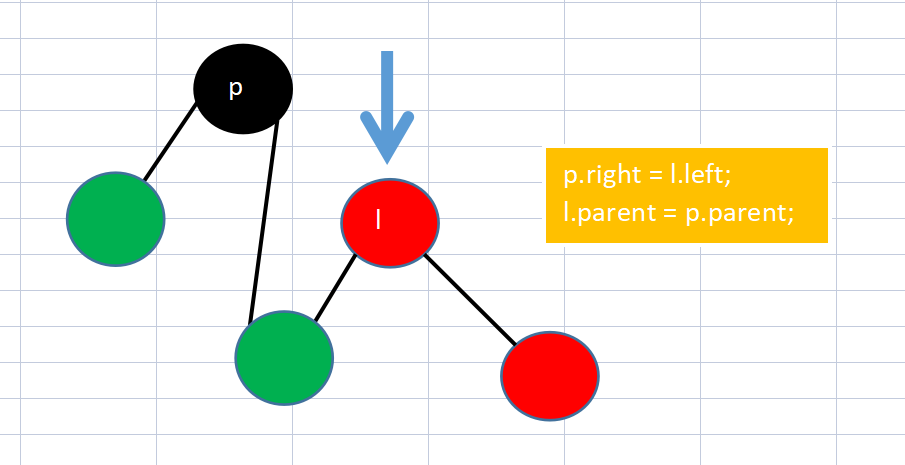
- Point the left of l to p
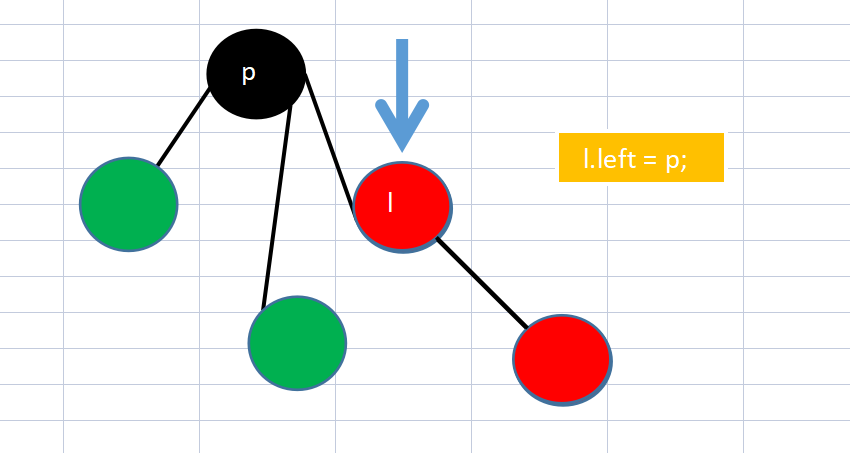
result:
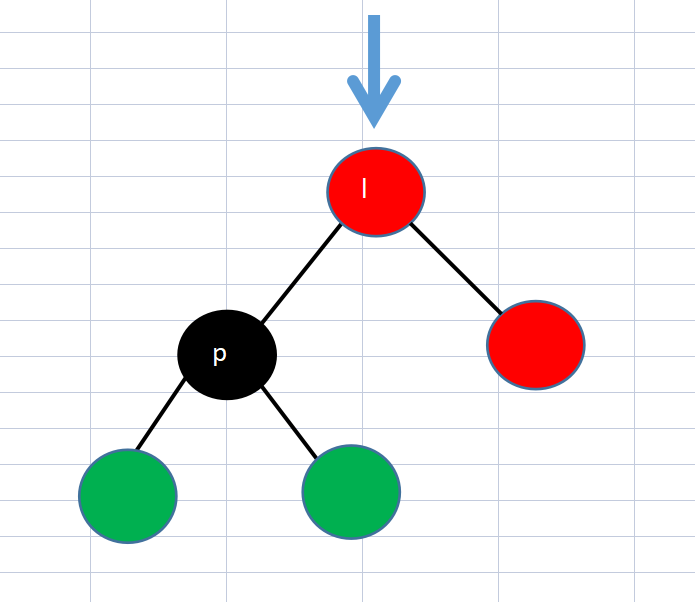
Note: every time the left and right nodes are exchanged, the direction of the parent node must be changed. At the same time, pay attention to whether the left or right of the parent node points to the child node. The above figure is omitted
So we have the following code:
Left hand code
//Take the p node as the rotation point
private void leftRotate(RBNode p) {
if(p!=null){
RBNode l=p.right;
setColor(l, p.color);
setColor(p, RED);
p.right = l.left;
//In the previous sentence, the direction is exchanged, so to modify the direction of the parent node, the direction is known
if (l.left != null) {
l.left.parent = p;
}
l.parent = p.parent;
//In the previous sentence, the direction is exchanged, so the direction of the parent node should be modified. The direction is unknown, so the direction should be judged
if (p.parent == null) {//If there is no description, the p node is the root node, and let the root node point to l
root = l;
} else if (p.parent.left == p) {//If the parent node is left
p.parent.left = l;
} else {//If it is the parent node, right
p.parent.right = l;
}
l.left = p;
//The parent node is processed and cannot be empty
p.parent = l;
}
}
Dextral diagram

Right hand code
Similarly, it is left-handed and will not be repeated
private void rightRotate(RBNode p) {
RBNode r = p.left;
setColor(r, getColor(p));
setColor(p, RED);
p.left = r.right;
if (r.right != null) {
r.right.parent = p;
}
r.parent = p.parent;
if (p.parent == null) {
root = r;
} else if (p.parent.left == p) {
p.parent.left = r;
} else {
p.parent.right = r;
}
r.right = p;
p.parent = r;
}
New node
AVL tree method search location
Create a put method in RBTree class, and find it first:
class RBTree<K extends Comparable<K>,V>{
public void put(K key,V value){
if(key==null){
throw new RuntimeException("Null pointer exception");
}
//If root is empty, it indicates the first element, and you can modify root directly
if(null == root){
//The default color is black
root=new RBNode<>(key,value==null?key:value,null);
return;
}
//com records the comparison value, which is used to record whether the position of the inserted node is left or right in the direction of the parent node
int com;
//Record the parent node of the inserted node. Because the inserted node cannot immediately become the root node (subsequent adjustments may become the parent node), the parent node must exist
RBNode parentTail;
//Start the search from the root node, followed by parentTail
RBNode tail=root;
do{
//Record parent node
parentTail=tail;
//Compare the inserted value with the value and of tail search, and record with com
com=key.compareTo((K) tail.key);
if(com<0){
//Search left
tail=leftOf(tail);
}else if (com>0){
//Search right
tail=rightOf(tail);
}else {
//If it is the same, it will directly overwrite the current value, because it does not change the balance of the tree and directly end the program
tail.value=value==null?key:value;
return;
}
}while (tail!=null);//Terminate search criteria
//Create a new section to store the incoming data
RBNode newRBNode=new RBNode<>(key,value==null?key:value,parentTail);
//The left and right assignment operations of the parent node are performed according to the com size
if (com<0){
parentTail.left=newRBNode;
}else {
parentTail.right=newRBNode;
}
}
fixAfterPut(newRBNode);
}
Do you think it's over( How can there be a code I haven't seen!!!)

Yes, yes, and the fixAfterPut function!!!
Let's take a look at all the possible results after AVL search!
Illustration of red black insertion (take the left as an example)
According to the situation that the inserted node corresponds to the 234 tree:

- The added color should be set to red first to prevent direct impact on the balance of red and black trees
- When the parent node is black, no operation is required.
- When the parent node is red, it is necessary to judge whether the uncle node exists
- If the uncle node does not exist (the third type), judge which node is the father node and make one or two rotations
- If the uncle node exists, change the color (the fourth kind), and judge the grandfather node as a new node to enter the cycle
- Root black
The second of case 3:

Case 3:

The first of case 4:
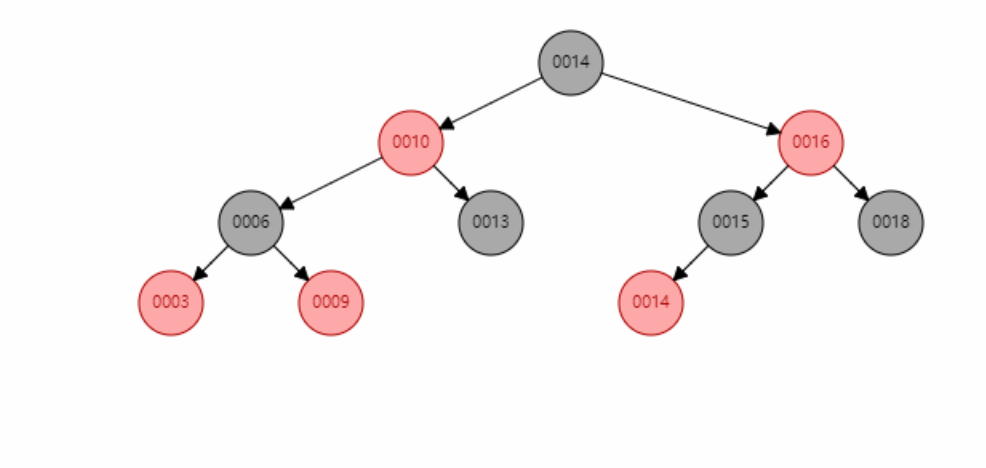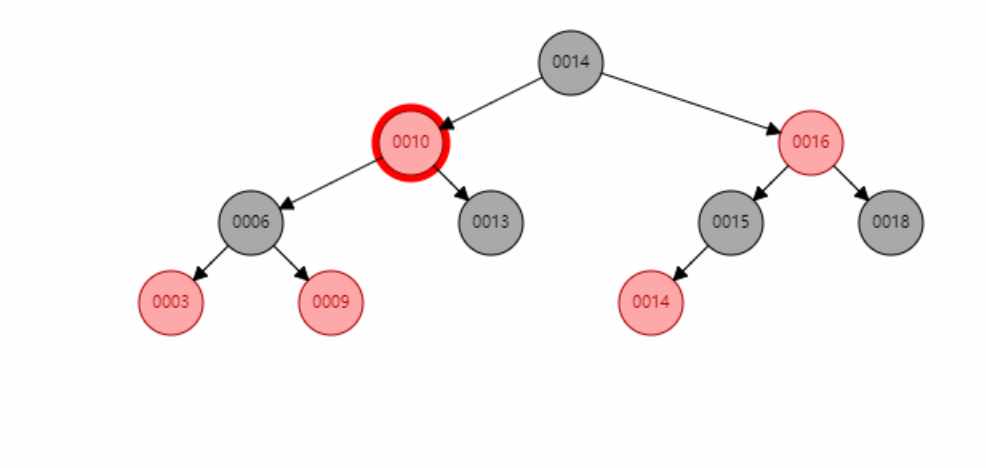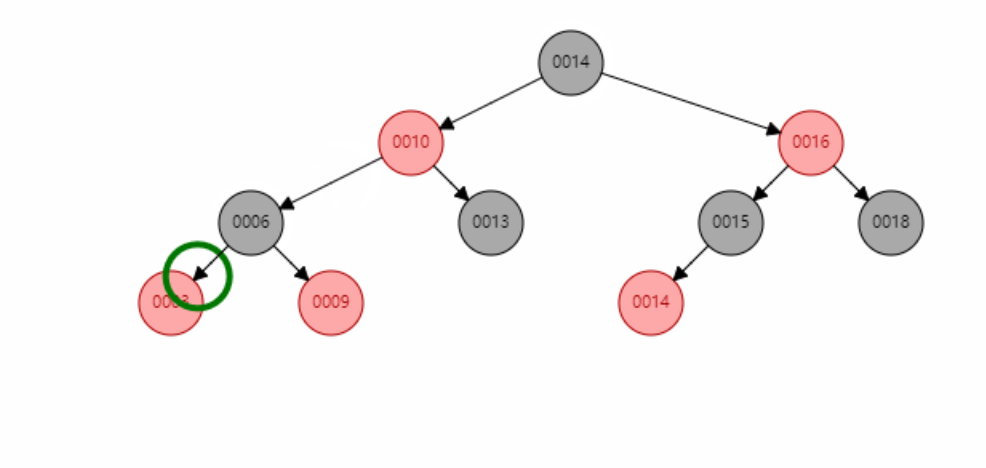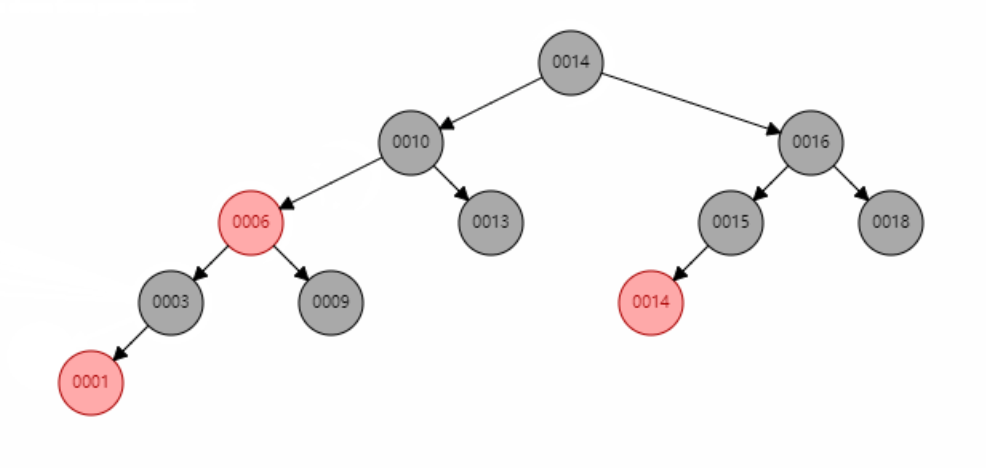
The second of scenario 4:
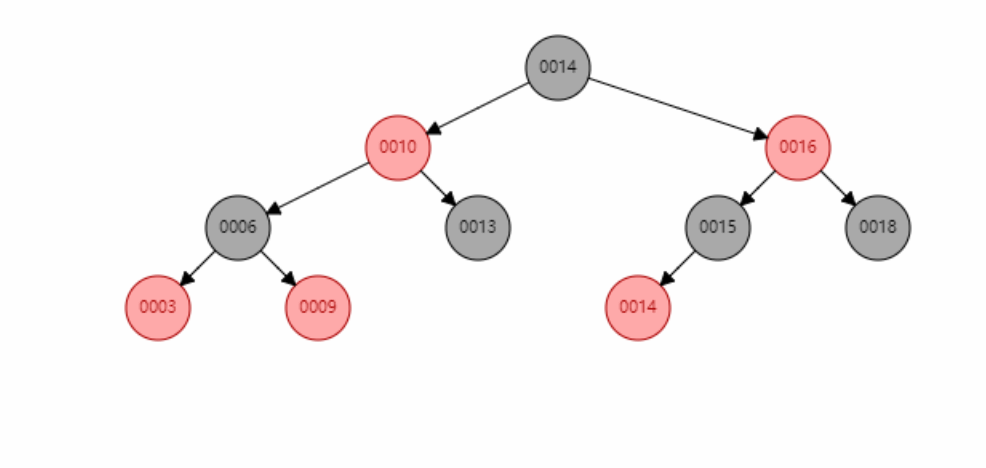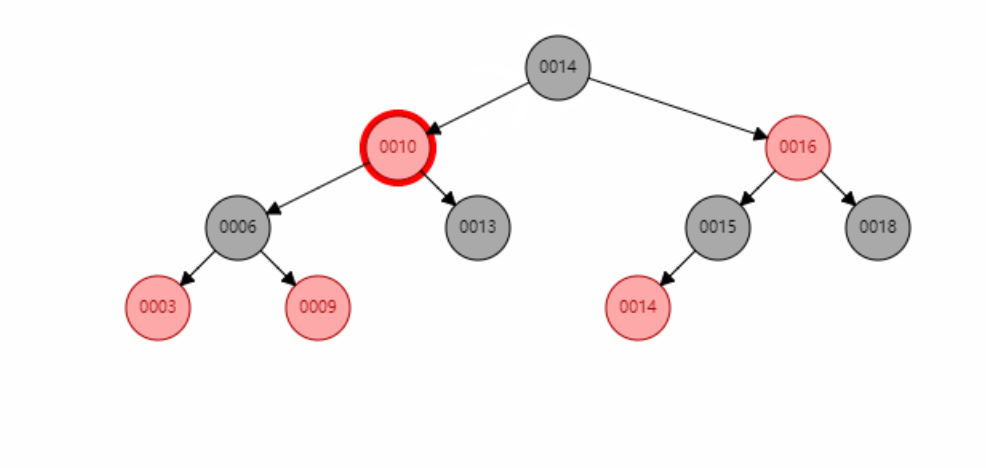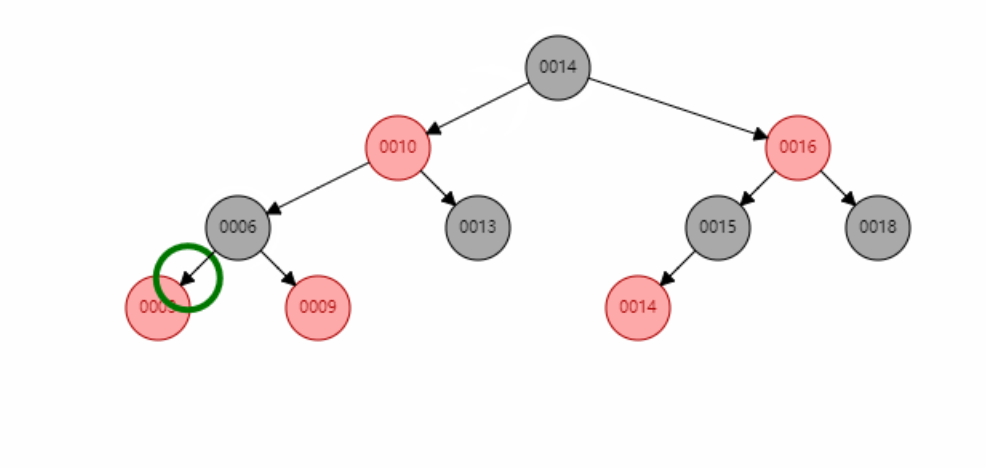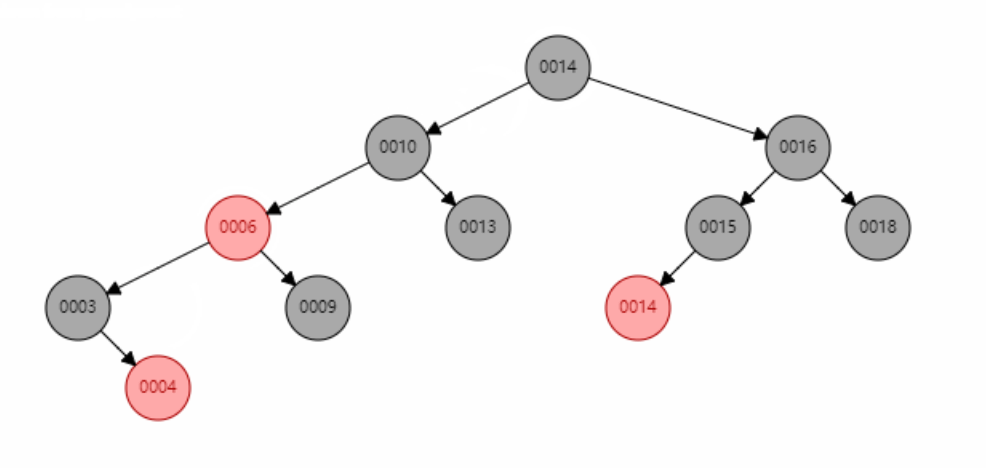
Flow chart of red black insertion
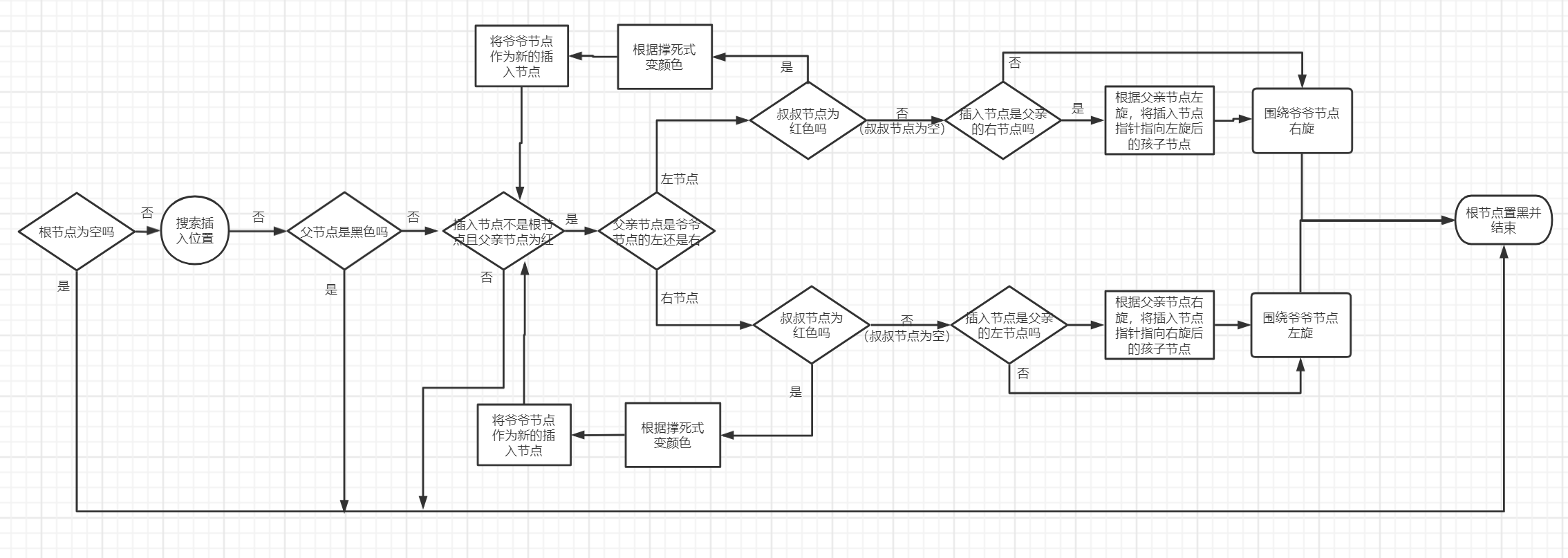
Code explanation
This case of empty root has been excluded before searching.
private void fixAfterPut(RBNode newRBNode) {
//Set the new node to red
setColor(newRBNode,RED);
//If the parent node of the new node is black, exit directly
//It's OK without this judgment, because it won't enter the cycle, but it's easy to understand
if(getColor(parentOf(newRBNode))==BLACK){
return;
}
//The new node is not the root node, and the parent node is red
//(if the parent node is red, it is used as the out of loop condition and has no effect on the first in loop
while (newRBNode != root&&getColor(parentOf(newRBNode))==RED){
//Add pointers to Grandpa and father for easy understanding
RBNode grandFather=parentOf(parentOf(newRBNode));
RBNode father=parentOf(newRBNode);
//Judge whether the father is Grandpa's left node or right node, and judge whether the uncle is around grandpa's node in turn
if(leftOf(grandFather)==father){
//Determine the uncle node, which may be null
RBNode uncle=rightOf(grandFather);
//Is the uncle node empty or red
//(it cannot be black. If it is black, the previous trees are unbalanced)
if(getColor(uncle)==RED){
//Dead change color
setColor(grandFather,RED);
setColor(uncle,BLACK);
setColor(father,BLACK);
//Replace grandpa with a new node and cycle again
newRBNode=grandFather;
}else {//Empty node:
//Do you need left-hand adjustment
if(rightOf(father)==newRBNode){
leftRotate(father);
//Point to new node location
newRBNode=father;
}
//Turn right according to the node
//After right rotation, the father of the newRBNode node is black
//There is no need to change the color manually because it has changed during rotation, but be careful to verify
rightRotate(grandFather);
}
}else {//The last code is the same
RBNode uncle=leftOf(grandFather);
if(getColor(uncle)==RED){
setColor(grandFather,RED);
setColor(uncle,BLACK);
setColor(father,BLACK);
newRBNode=grandFather;
}else {
if(leftOf(father)==newRBNode){
rightRotate(father);
newRBNode=father;
}
leftRotate(grandFather);
}
}
}
//Set the root node to black to prevent other operations from turning red
setColor(root,BLACK);
}
New code integration (put)
public void put(K key,V value){
if(null == root){
root=new RBNode<>(key,value==null?key:value,null);
return;
}
int com;
RBNode tail=root;
RBNode parentTail;
if(key==null){
throw new RuntimeException("Null pointer exception");
}
do{
parentTail=tail;
com=key.compareTo((K) tail.key);
if(com<0){
tail=leftOf(tail);
}else if (com>0){
tail=rightOf(tail);
}else {
tail.value=value==null?key:value;
return;
}
}while (tail!=null);
RBNode newRBNode=new RBNode<>(key,value==null?key:value,parentTail);
if (com<0){
parentTail.left=newRBNode;
}else {
parentTail.right=newRBNode;
}
fixAfterPut(newRBNode);
}
private void fixAfterPut(RBNode newRBNode) {
setColor(newRBNode,RED);
while (newRBNode != root&&getColor(parentOf(newRBNode))==RED){
RBNode grandFather=parentOf(parentOf(newRBNode));
RBNode father=parentOf(newRBNode);
if(leftOf(grandFather)==father){
RBNode uncle=rightOf(grandFather);
//Empty or black do not enter
if(getColor(uncle)==RED){
setColor(grandFather,RED);
setColor(uncle,BLACK);
setColor(father,BLACK);
newRBNode=grandFather;
}else {
if(rightOf(father)==newRBNode){
leftRotate(father);
newRBNode=father;
}
rightRotate(grandFather);
}
}else {
RBNode uncle=leftOf(grandFather);
if(getColor(uncle)==RED){
setColor(grandFather,RED);
setColor(uncle,BLACK);
setColor(father,BLACK);
newRBNode=grandFather;
}else {
if(leftOf(father)==newRBNode){
rightRotate(father);
newRBNode=father;
}
leftRotate(grandFather);
}
}
}
setColor(root,BLACK);
}
Delete node
To delete:
- Get the deleted node (getNode) of the corresponding Key value
- After confirming to delete a node, delete it through a function (deleteNode)
- Another function is created to adjust the balance of the red black tree after deletion (fixAfterRemove)
- Integrate the above three methods (remove)
Find the node (getNode)
The search method has no effect on the red black tree balance, so it can be queried as an AVL tree. Look directly at the code
private RBNode getNode(K key){
RBNode tail=root;//The pointer starting from the root node is used to determine the direction of subsequent searches
if(root==null){
//If root is empty, there can be no corresponding value
throw new RuntimeException("Can't be empty");
}
//If the searched node is not empty, continue to search left and right
while (tail!=null){
//The left and right positions are determined by comparison
int cmp=key.compareTo((K)tail.key);
if(cmp<0){
//Find left
tail=leftOf(tail);
}else if (cmp>0){
//Find right
tail=rightOf(tail);
}else {
//If the search result is found, the value is returned
return tail;
}
}
//Out of the loop means that there is no such value, and null is returned
return null;
}
Delete anchor node
Delete node analysis
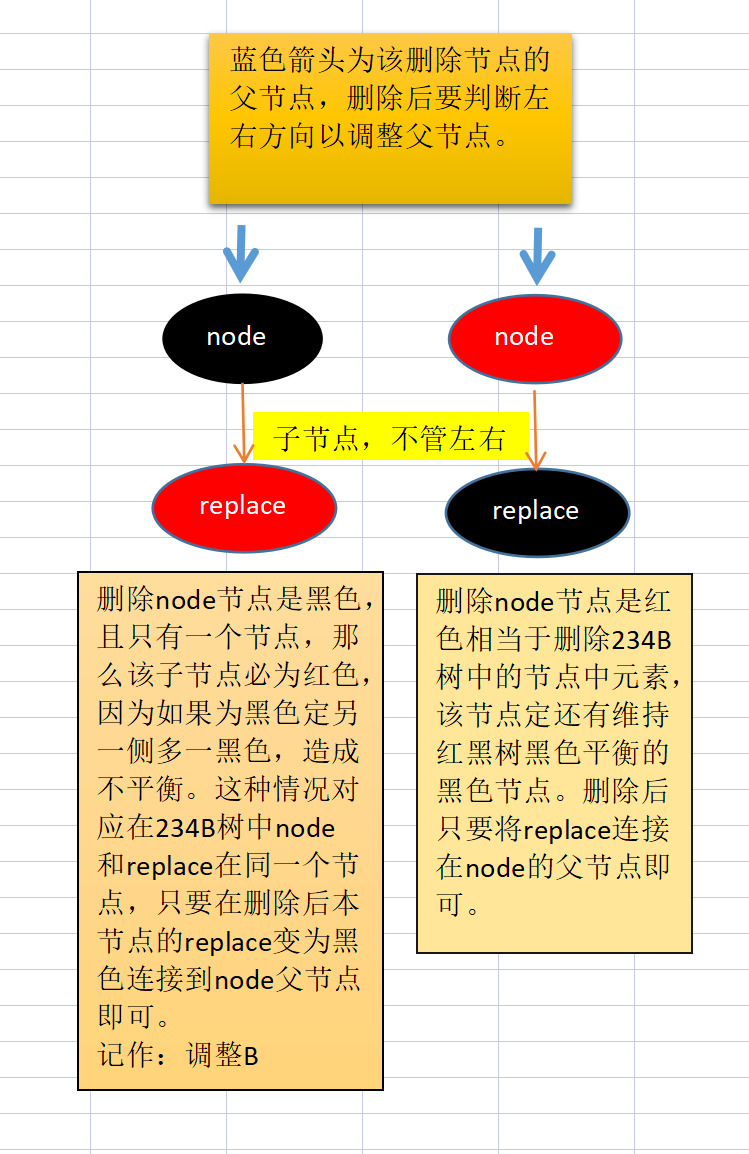
Note: node refers to the deleted node, and replace refers to the node that replaces the node after the node is deleted
Case 1: the deleted node has no child nodes

Case 2: the deleted node has a child node
Case 3: the deleted node has two child nodes
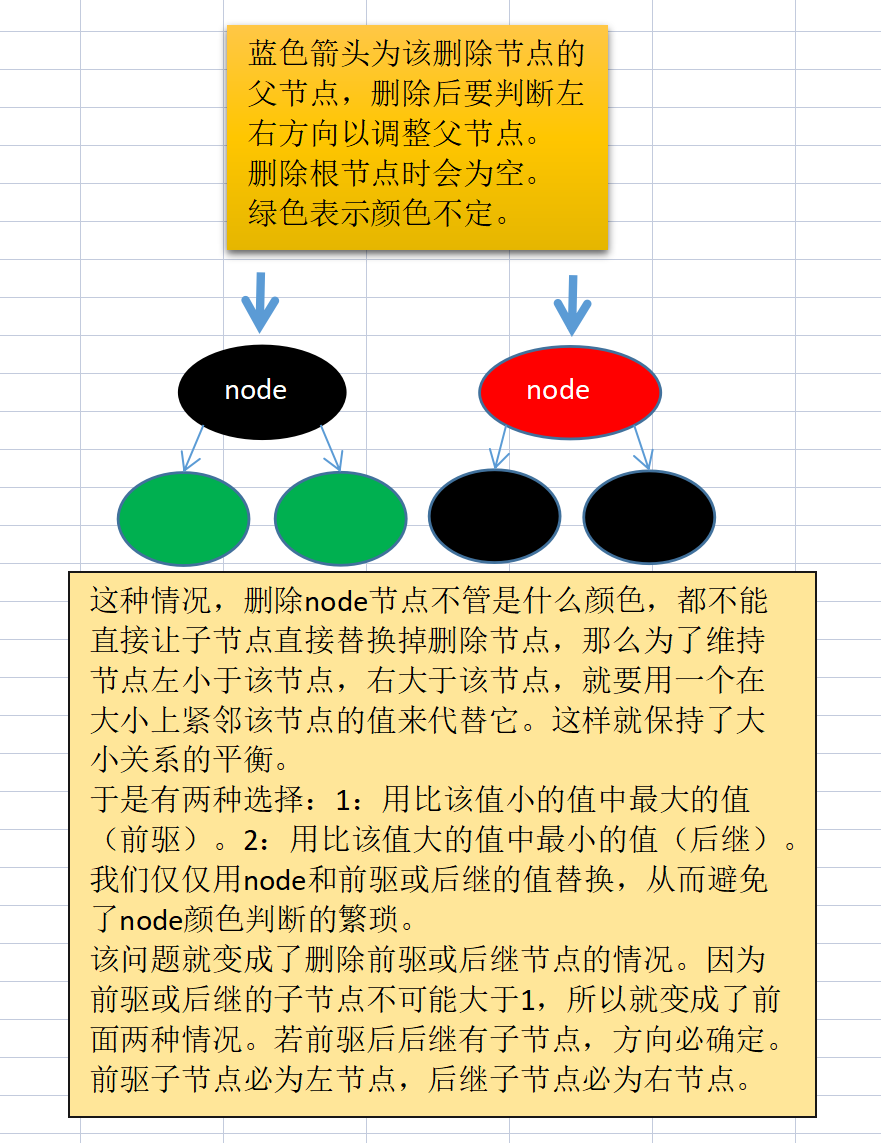
Note: in case 1 and case 2, when the deleted node node is red, it does not need to be adjusted. Only the black node can be adjusted!!!
Code decomposition
Because case 3 will eventually pass through the precursor and then go to case 1 or case 2. So we only need to discuss case 3 before case 1 and case 2.
Situation III
Precursor node
//Node is the node that needs to be deleted and looks for its precursor node.
private RBNode pre(RBNode node){
//Since those smaller than the node are on the left of the node, and those with the largest values are on the right of the left subtree of the node
//Since the node node has two child nodes, there is no need to judge whether the left node is empty
RBNode l=leftOf(node);
//Find maximum right
while (l.right!=null){
l=l.right;
}
return l;
}
Successor node
private RBNode suc(RBNode node){
//Since those larger than the node are on the right side of the node, and those with the smallest values are on the left side of the right subtree of the node
//Since the node node has two child nodes, there is no need to judge whether the right side of the node is empty
RBNode r=rightOf(node);
while (r.left!=null){
r=r.left;
}
return r;
}
Case III - > case I and II
if(leftOf(node)!=null&&rightOf(node)!=null){
RBNode pre = pre(node);//The precursor node is used here
//Assign a value. Because pre will be deleted as a new node after assigning a node, its value is not important
node.key=pre.key;
node.value=pre.value;
//The successor node acts as a new deleted node
node=pre;
}
Analysis and determination of replace
How can replace be determined as the node that replaces the node after the node is deleted?
- Point to a non empty node when the node has nodes (case 2)
- If there is no node, it points to null (case 1)
Writing method I
RBNode replace;
//When the left is empty and the right is not empty, replace points to the right (case 2)
if(leftOf(node)==null&&rightOf(node)!=null){
replace=rightOf(node);
//When the right is empty and the left is not empty, replace points to the left (case 2)
}else if (leftOf(node)!=null&&rightOf(node)==null){
replace=leftOf(node);
}else {//Both sides are empty (case 1)
replace=null;
}
/*
leftOf(node)!=null&&rightOf(node)!=null Where's the situation?
This is case 3, which has been converted to case 1 or 2, so it cannot exist
*/
Writing method 2
The code of method 1 is written as a trinocular operator, which is as follows:
RBNode replace=leftOf(node)!=null?leftOf(node):rightOf(node);
if processing II
//Now there are only cases 1 and 2. The difference between cases 1 and 2 is whether replace is null
if(replace!=null){//Case 2 entry
//Point the child node of the node parent node (whether it exists or not is uncertain, which needs to be discussed) to replace
//To achieve the effect of deleting node
replace.parent=parentOf(node);
//When the deleted node node in case 2 is the root node (case 3 is impossible, because it is impossible to convert to the deleted precursor node as the root node)
//At this time, there is only one red node under the root node, and replace is the red node
//parentOf(node) is null and replace.parent is null
//Therefore, judge whether the node is the root node, that is, judge whether parentOf(node)==null is true
if(parentOf(node)==null){
//If the root node is replaced by yong red replace, the color will be adjusted later because the deleted node is black
root=replace;
}else if(node==leftOf(parentOf(node))){//Delete the left child node whose node is the parent node
node.parent.left=replace;
}else {//Delete the right child node whose node is the parent node
node.parent.right=replace;
}
//Handle and delete all pointer relationships of node node
node.left=node.right=node.parent= null;
//❤❤❤❤❤❤❤❤❤❤❤❤❤❤❤❤❤❤ Adjustment B ❤❤❤❤❤❤❤❤❤❤❤❤❤❤❤❤❤❤
//In case 2, the deleted node is black, including the case where the deleted node is the root node
if(getColor(node)==BLACK){
//replace!= If NULL is determined to be true, the replace node must be red
//Because the original node has only one child node in one direction, this child node is replace. In order to maintain the black balance, it is red
//In fact, this situation only needs one sentence, but it is put in the function for modularity
//After entering fixAfterRemove, because replace must be red, the loop in fixAfterRemove cannot be entered (fixAfterRemove function is later)
fixAfterRemove(replace);
/*
If you enter fixAfterRemove processing, you can also directly change replace to black
Replace fixAfterRemove with the following sentence
setColor(replace,BLACK);
❤❤❤❤❤❤❤❤❤It is recommended to use setColor(replace,BLACK); This can be better understood
*/
}
}
else processing I
//Entering else means that the node to be deleted has no child nodes, which is case 1
//Since there are no child nodes, replace==null here. Just a hint seems useless
else {
//❤❤❤❤❤❤❤❤❤❤❤❤❤❤❤❤❤❤ Adjustment A ❤❤❤❤❤❤❤❤❤❤❤❤❤❤❤❤❤❤
//In red, no adjustment is required, just adjust the pointer of the child node and the parent node
//node black before entering the adjustment
if(getColor(node)==BLACK){
fixAfterRemove(node);
}
//After adjustment, the pointer of the child node and the parent node is adjusted
//But how do you know he has a parent node? So we need to discuss
if(parentOf(node)!=null) {
if (node == leftOf(parentOf(node))) {//Delete the node. The right node is the successor
node.parent.left = null;
} else {
node.parent.right = null;
}
node.parent = null;
}else {
//Node has no parent node, is the root node, and has no child nodes
//Note: to delete the root node, it must be empty directly
root=null;
}
}
Note: just put the above code in the function named deleteNode in order
Code deleteNode integration
private RBNode deleteNode(RBNode node) {
if (leftOf(node) != null && rightOf(node) != null) {
RBNode pre = pre(node);
node.key = pre.key;
node.value = pre.value;
node = pre;
}
RBNode replace = leftOf(node) != null ? leftOf(node) : rightOf(node);
if (replace != null) {
replace.parent = parentOf(node);
if (parentOf(node) == null) {
root = replace;
} else if (node == leftOf(parentOf(node))) {
node.parent.left = replace;
} else {
node.parent.right = replace;
}
node.left = node.right = node.parent = null;
if (getColor(node) == BLACK) {
fixAfterRemove(replace);
}
}
else {
if (getColor(node) == BLACK) {
fixAfterRemove(node);
}
if (parentOf(node) != null) {
if (node == leftOf(parentOf(node))) {
node.parent.left = null;
} else {
node.parent.right = null;
}
node.parent = null;
} else {
root = null;
}
}
return null;
}
Balance adjustment after deletion (fixAfterRemove)
Ha hahahahahahahaha ha the most difficult to understand red and black adjustment, it's coming!!!

remember well:
1. The deleted node is black, which is represented by yellow
2. Here is only an example of deleting a node as the left child of the parent node
3. Our code can change the color when it rotates left / right. After giving the color of the rotated node to the right / left child node, it turns red
When will it need to be adjusted?
A: the deleted node is black, and the black node has no child nodes
What is the fundamental goal of the adjustment?
A: look for nodes that can be moved (red) and turn black to make up for the black imbalance caused by deleting one side of the black node.
Brothers are black and have red child nodes 1-3
This black sibling node locates the sibling node in the 234 tree.
The sibling node has no child red node, which is discussed at the end.
The children of sibling nodes cannot be black because of imbalance.
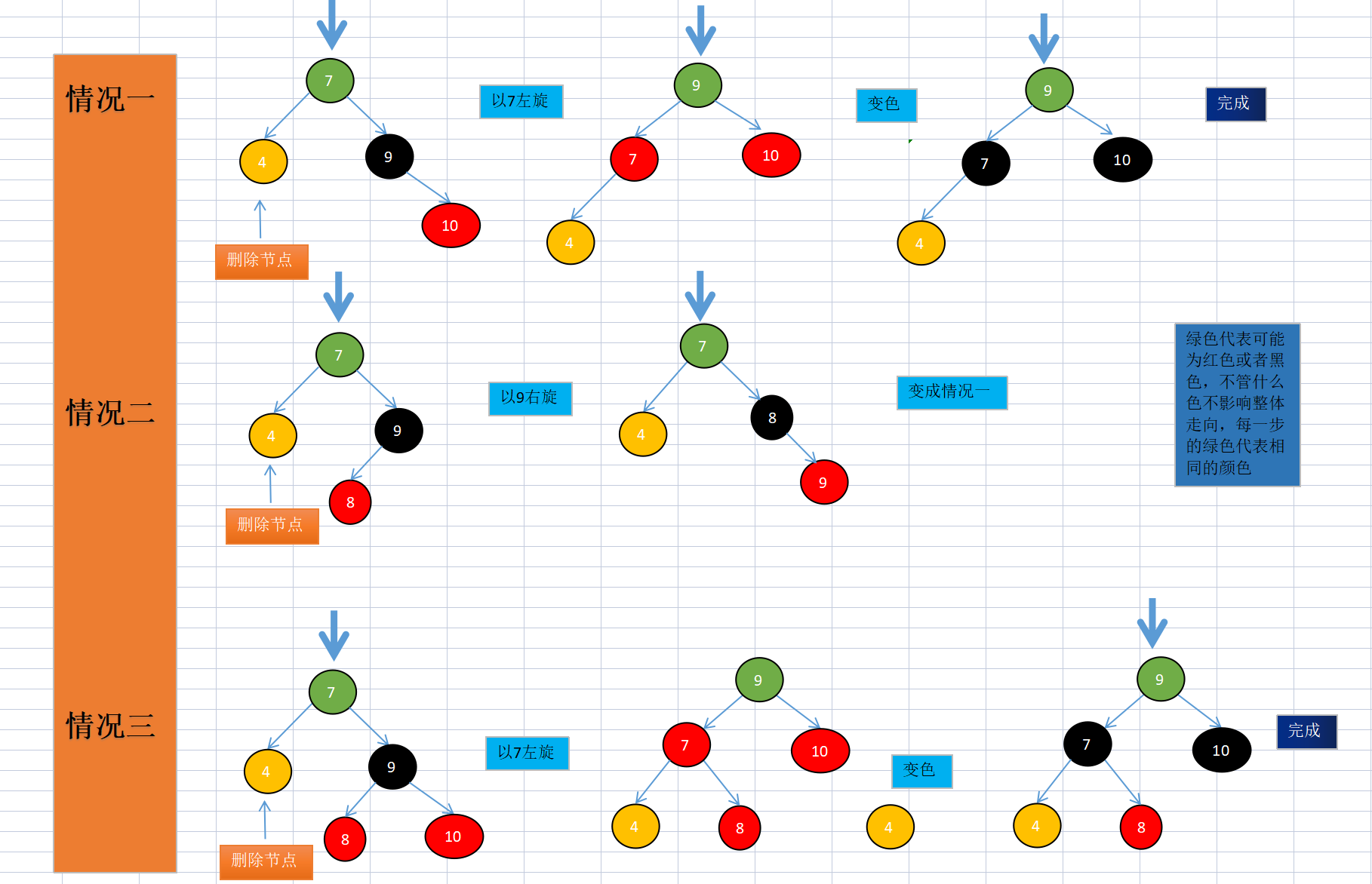
//It is assumed that the deleted node is the left of the parent node, so the brother must be the right
RBNode rBro=rightOf(parentOf(node));
//getColor(leftOf(rBro))==RED can be omitted later, because we give priority to judging that the left and right sibling nodes are black later
//BLACK is returned by default when the borrowing point is empty
if(getColor(rightOf(rBro))==BLACK&&getColor(leftOf(rBro))==RED){
//Left handed sibling node
rightRotate(rBro);
//Point the pointer to the current sibling node
rBro=rightOf(parentOf(node));
}
//Left hand rotation
leftRotate(parentOf(node));
//Balance color
setColor(parentOf(node),BLACK);
setColor(rightOf(rBro),BLACK);
(false) brother is red 4
Q: why can't the node with red brother turn to the left and turn black?
A: if the brother is red, there must be two black under the red node. If the red goes directly, the two black nodes cannot be processed, so it is necessary to turn left to turn the brother into black.
Why are they called fake brothers?
A: the red node is the parent element in the 234 tree

//Judge whether it is a real brother. The RED color is a false brother. The brother node is the father in the 234 tree
if(getColor(rBro)==RED){
//Rotate left around the parent node
leftRotate(parentOf(node));
//Adjust the pointer to true brother
rBro=rightOf(parentOf(node));
}
Brother is black without red node 5
Before we talk about this situation, we have a few thoughts:
Seven thoughts:
Think 1: when is there a situation where brothers are black and have no red nodes?
A: (false) the brother is red. After 4 rotation, the latter already exists. Therefore, the judgment must be after case 4 when the (false) brother is red
Thinking 2: what is the impact of deleting the black node on the corresponding 234 tree?
A: mapping on the 234 tree is equivalent to deleting an entire node, resulting in the imbalance of the 234 tree.
Thinking 3: what is the general idea of 234 tree processing?
A: add a node on the node path (the value of the node is indirectly from the element in the sibling node) or reduce the whole tree by one layer. 234 the nodes in the tree correspond to the black nodes in the red black tree
Thinking 4: if a node comes indirectly from a sibling node, then 4 nodes will become 3 nodes, and 3 nodes will become 2 nodes. However, the original number of child nodes of the sibling node will remain unchanged, so that the tree will not comply with the B-tree principle?
A: No, when we indirectly change the value of the sibling node to delete the tree node, the parent node of a child tree changes (note the parent node of - 76). This corresponds to left-right rotation in red black trees (not necessarily once)

Thinking 5: how to deal with the problem of adding nodes 234 tree itself?
A: look for the sibling node of the deleted node. If the sibling node is greater than 1, the sibling element (- 756) will be operated. If the sibling node is greater than 1, there are red child nodes corresponding to the sibling node in the red black tree

Think 6: what if the nearest node has no redundant elements?
A: treat the parent node as a deleted node and continue to look up in a loop, but only the sibling node and parent node of one element will be merged in the process. If the node reaches the child node of the root node, judge whether the node sibling node (the other direction of the root node) has redundant elements. If so, the value exchange will end at this time. However, if it still does not, the sibling node will be combined with the root node as the root node. In this way, the overall number of layers on the other side is reduced, that is, the balance effect is achieved by reducing the depth of the tree.

Thinking 7: what is the operation response of 234 tree in thinking 6 on red black tree?
A: before reaching the following node, the sibling nodes whose left and right child nodes are black (true black or null) will turn red (corresponding to the merging of siblings and parent nodes in 234 tree) until the child nodes of the sibling nodes are found to have red nodes. Then, according to the situation that the brothers are black and have red nodes, 1-3
Figure 1 of thinking 7:
Objective: delete node 1 (omitted from the right)
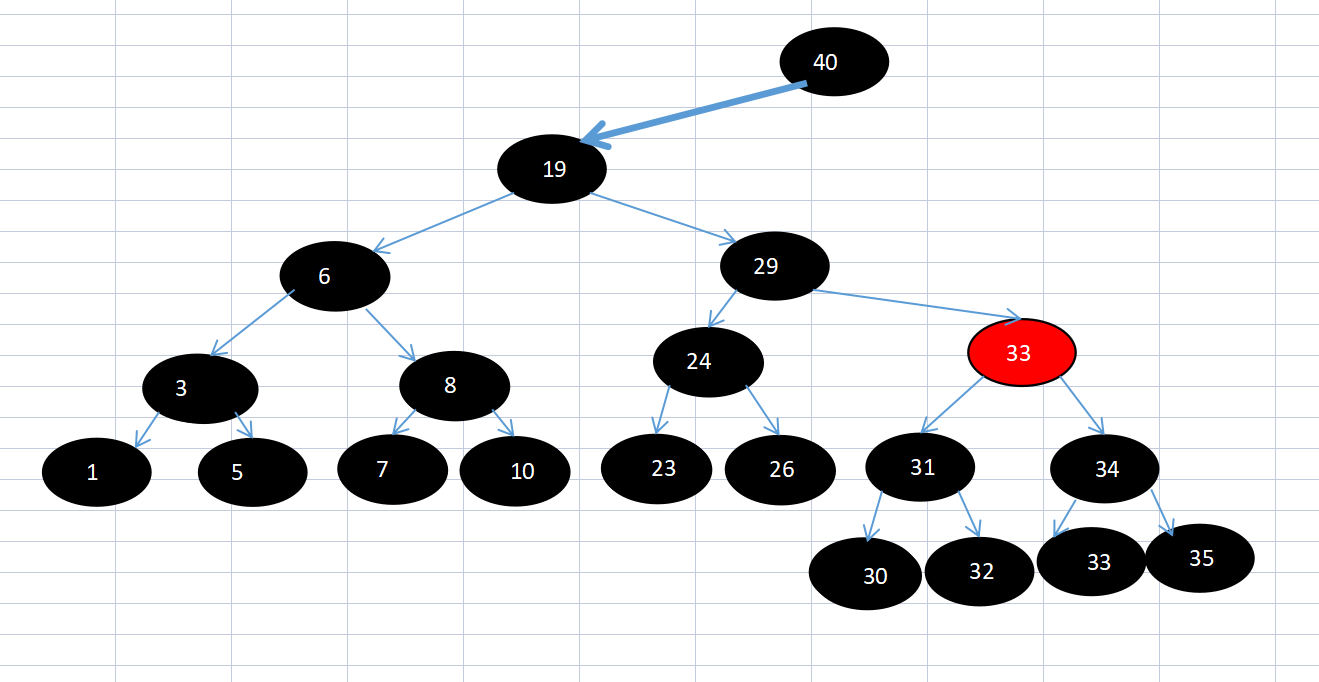
Figure 2 of thinking 7:
Because the sibling node of 1 is 5, and the left and right child nodes of 5 are empty (i.e. black), it does not meet the conversion conditions, and the sibling node 5 becomes red. The pointer points to the previous element 3.
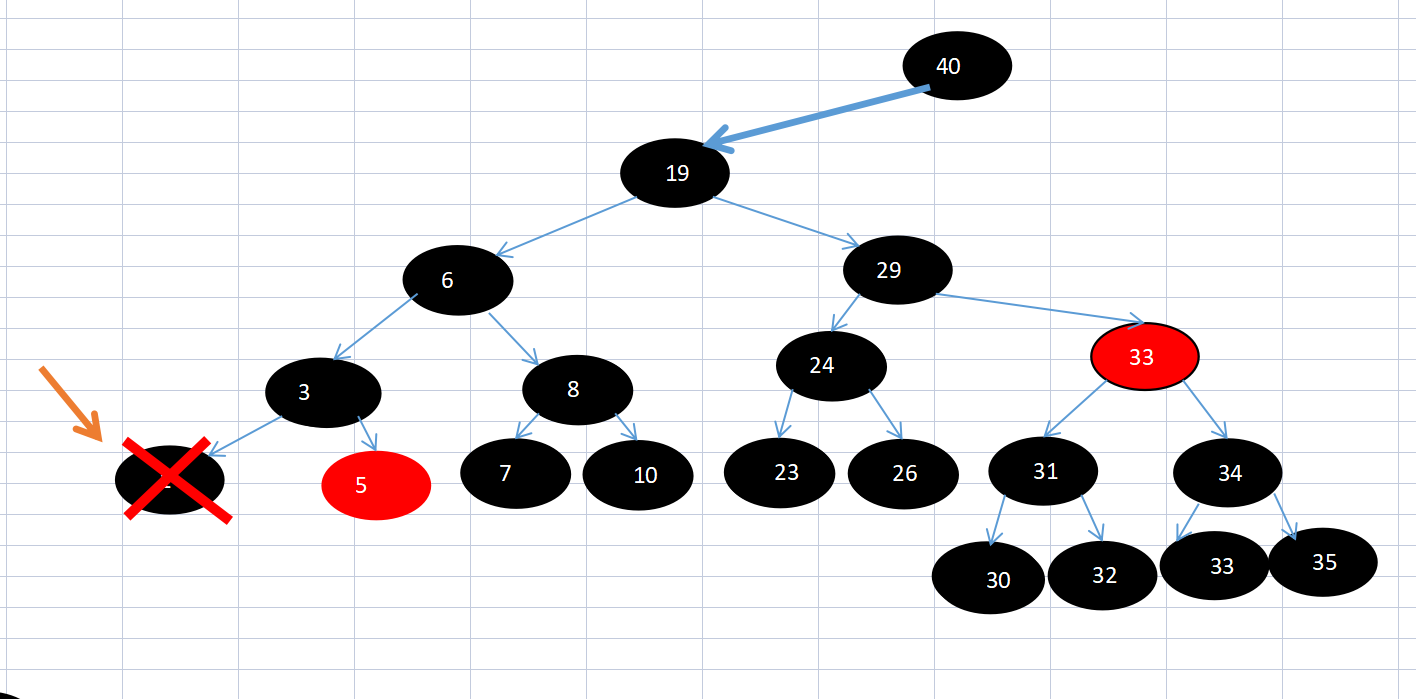
Figure 3 of thinking 7:
Because the sibling node of 3 is 8, and the left and right child nodes of 8 are black, which does not meet the conversion conditions, the sibling node 8 becomes red. The pointer points to the previous element 6.
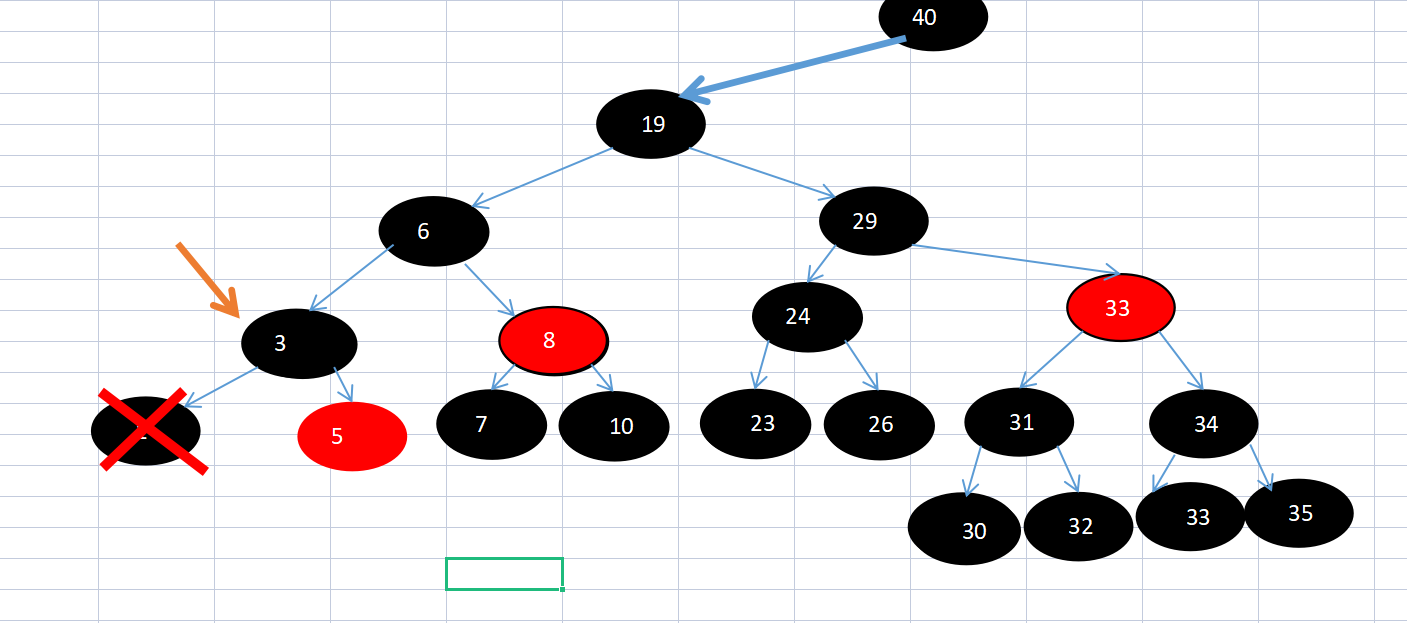
Figure 4 of thinking 7:
Because the brother node of 6 is 29, the left and right child nodes of 29 have red, which meets the conversion conditions. According to the case 1-3 where the brother is black and has red child nodes, it is sufficient to change the color after left rotation.
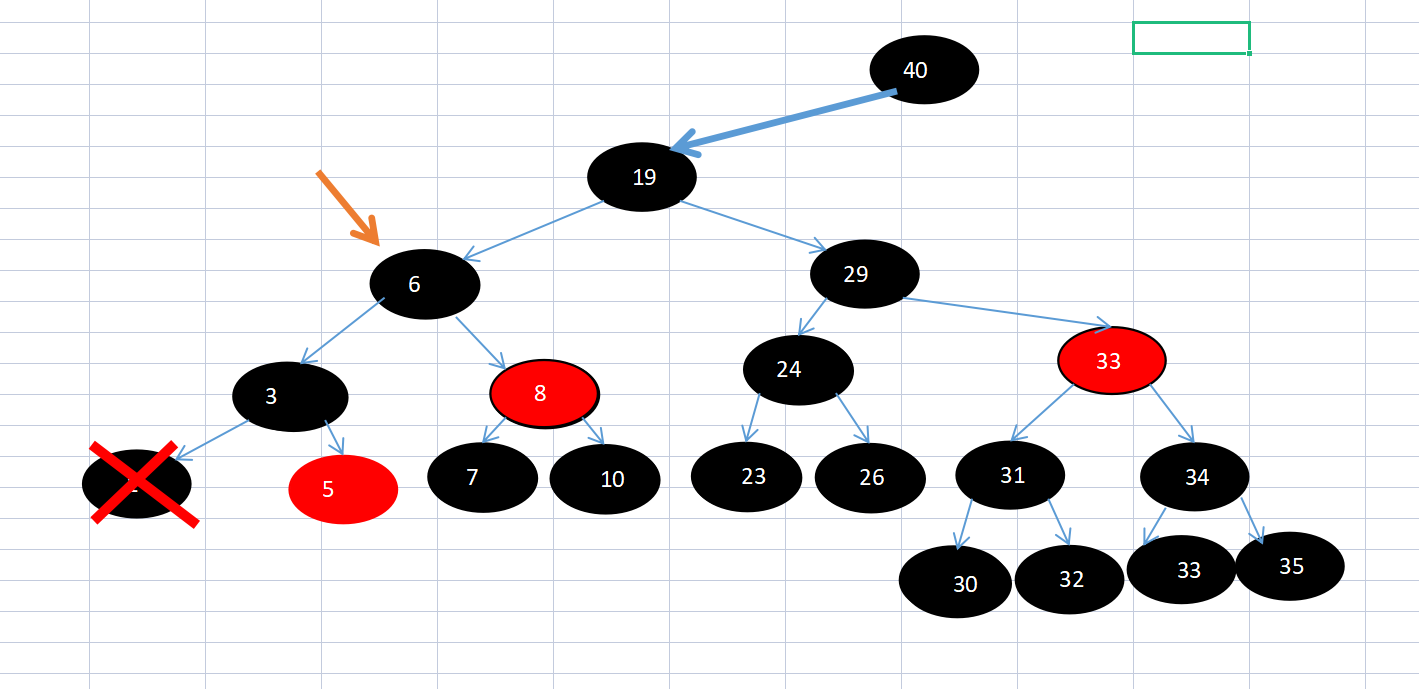
Figure 5 of thinking 7:
After left-handed rotation.

Figure 6 of thinking 7:
Change the color (set the left and right child nodes of the rotation node to black). When finished, the black balance is met

Continued thinking 7: what if you can't finish it when you reach the root node?
A: this operation must be balanced in front of the root node. Don't forget that there are two ways to become a balance tree:
First, by adding black nodes (the process of thinking about seven)
The second is to reduce the number of black layers of red black tree (corresponding to the number of node layers of 234 tree)
There are three situations near the root node:
1: The child nodes in the other direction of the root node are red:
The situation is the same as that in case 4 when the (false) brother is red
The process is the same as thinking about seven, but the parent node is the root node. When turning left and right
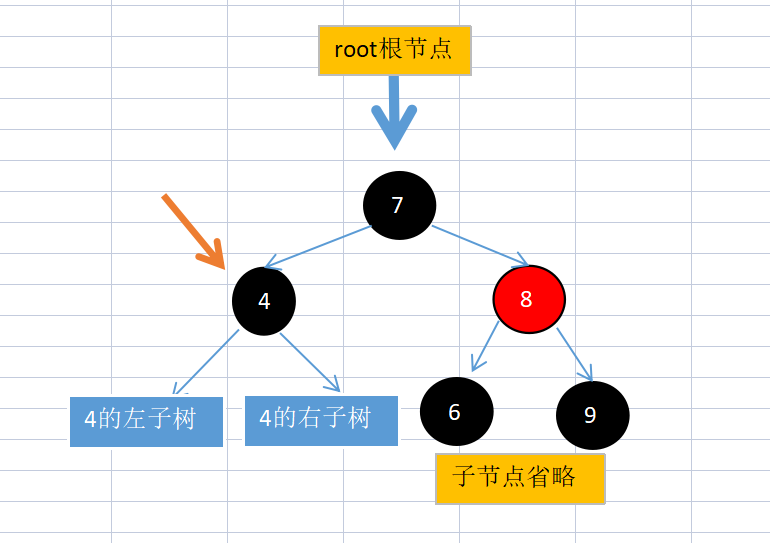
2: The child node in the other direction of the root node is black, and the black node sub node has a red node:
It is the same as the case 1-3 when the brother is black and has red child nodes
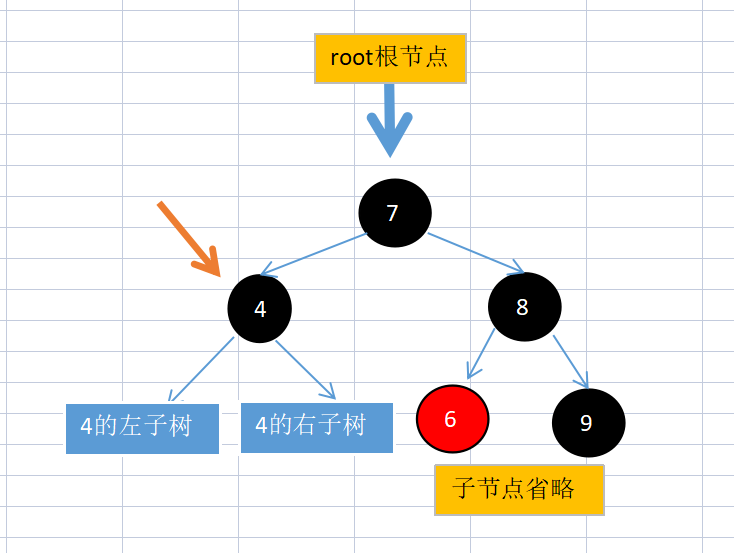
3: The child node in the other direction of the root node is black, and the black node sub node does not have a red node:
In this case, the normal program is not satisfied. 8 will be set to red, and the Yellow pointer will continue to point up to the root node. At this time, the loop will be forcibly exited.
Force it out of balance?
A: it's balanced. In the past, there was one black on the left of root node 7. At this time, 8 turns red. There is less black on the right of root node 7, so it's balanced

code
The code is the simplest, but....
//Enter the program when it is empty or two black, and directly enter the next cycle after execution
//Cyclic condition node= root&&getColor(node)==BLACK
if(getColor(leftOf(rBro))==BLACK&&getColor(rightOf(rBro))==BLACK){
setColor(rBro,RED);
node=parentOf(node);
}
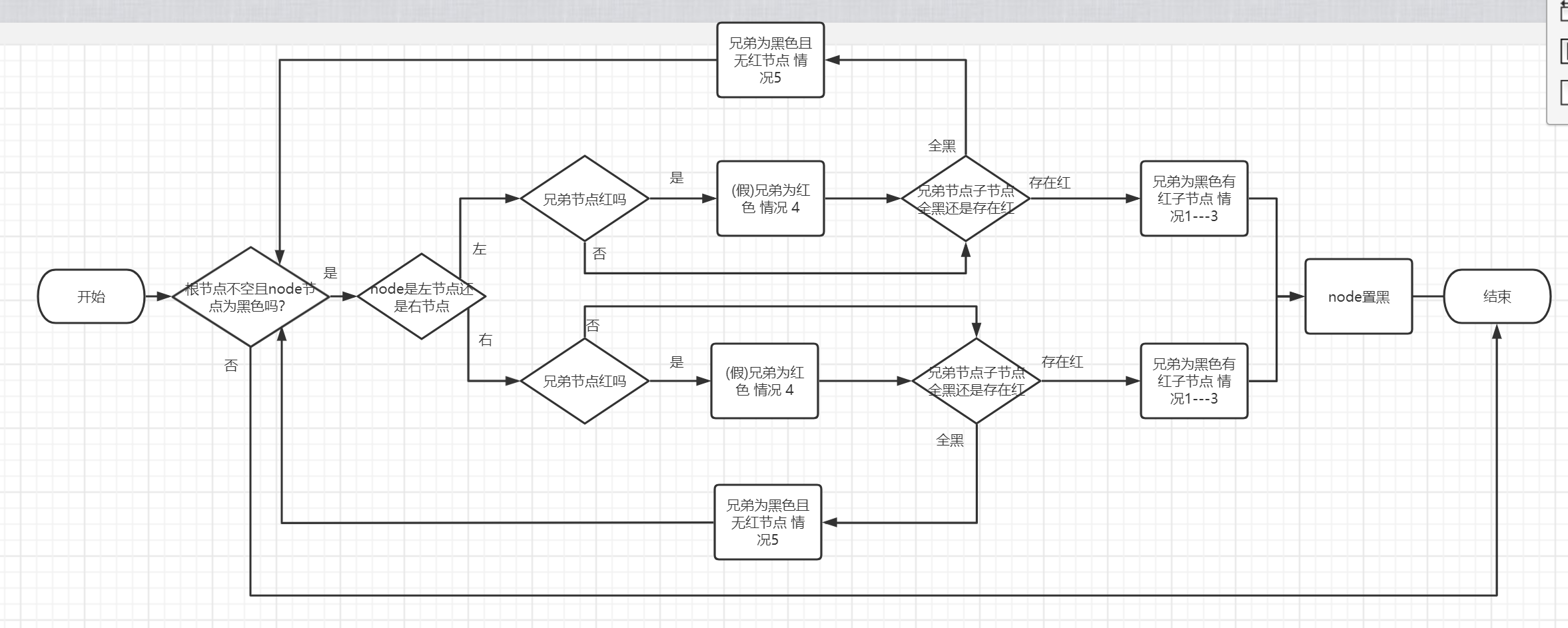
fixAfterRemove flowchart
Code for consolidation and adjustment (fixAfterRemove)
private void fixAfterRemove(RBNode node) {
while (node != root && getColor(node) == BLACK) {
//Delete the left node whose node is the parent node
if (node == leftOf(parentOf(node))) {
RBNode rBro = rightOf(parentOf(node));
//(false) brother is red, situation 4
if (getColor(rBro) == RED) {
leftRotate(parentOf(node));
rBro = rightOf(parentOf(node));
}
//Brother is black and there is no red node 5
if (getColor(leftOf(rBro)) == BLACK && getColor(rightOf(rBro)) == BLACK) {
setColor(rBro, RED);
node = parentOf(node);
} else {//Brothers are black with red nodes 1-3
if (getColor(rightOf(rBro)) == BLACK) {
rightRotate(rBro);
rBro = rightOf(parentOf(node));
}
leftRotate(parentOf(node));
setColor(parentOf(node), BLACK);
setColor(rightOf(rBro), BLACK);
break;
}
} else {//Delete the right node whose node is the parent node
RBNode lBro = leftOf(parentOf(node));
if (getColor(lBro) == RED) {
rightRotate(parentOf(node));
lBro = leftOf(node);
}
if (getColor(rightOf(lBro)) == BLACK && getColor(leftOf(lBro)) == BLACK) {
setColor(lBro, RED);
node = parentOf(node);
} else {//Two red or one red
if (getColor(leftOf(lBro)) == BLACK) {
leftRotate(lBro);
lBro = leftOf(parentOf(node));
}
rightRotate(parentOf(node));
setColor(parentOf(node), BLACK);
setColor(leftOf(lBro), BLACK);
break;
}
}
}
//The alternative borrowing point is red and directly turns black. There must be no node below this node
setColor(node, BLACK);
}
Three methods integration (remove)
public V remove(K key) {
RBNode node = getNode(key);
if (node == null) {
return null;
}
V oldValue = (V) node.value;
deleteNode(node);
return oldValue;
}
Delete code integration
public V remove(K key) {
RBNode node = getNode(key);
if (node == null) {
return null;
}
V oldValue = (V) node.value;
deleteNode(node);
return oldValue;
}
private RBNode getNode(K key) {
RBNode tail = root;
if (root == null) {
throw new RuntimeException("Can't be empty");
}
while (tail != null) {
int cmp = key.compareTo((K) tail.key);
if (cmp < 0) {
tail = leftOf(tail);
} else if (cmp > 0) {
tail = rightOf(tail);
} else {
return tail;
}
}
return null;
}
private RBNode deleteNode(RBNode node) {
if (leftOf(node) != null && rightOf(node) != null) {
RBNode pre = pre(node);
node.key = pre.key;
node.value = pre.value;
node = pre;
}
RBNode replace = leftOf(node) != null ? leftOf(node) : rightOf(node);
if (replace != null) {
replace.parent = parentOf(node);
if (parentOf(node) == null) {
root = replace;
} else if (node == leftOf(parentOf(node))) {
node.parent.left = replace;
} else {
node.parent.right = replace;
}
node.left = node.right = node.parent = null;
if (getColor(node) == BLACK) {
fixAfterRemove(replace);
}
}
else {
if (getColor(node) == BLACK) {
fixAfterRemove(node);
}
if (parentOf(node) != null) {
if (node == leftOf(parentOf(node))) {
node.parent.left = null;
} else {
node.parent.right = null;
}
node.parent = null;
} else {
root = null;
}
}
return null;
}
private void fixAfterRemove(RBNode node) {
while (node != root && getColor(node) == BLACK) {
if (node == leftOf(parentOf(node))) {
RBNode rBro = rightOf(parentOf(node));
if (getColor(rBro) == RED) {
leftRotate(parentOf(node));
rBro = rightOf(parentOf(node));
}
if (getColor(leftOf(rBro)) == BLACK && getColor(rightOf(rBro)) == BLACK) {
setColor(rBro, RED);
node = parentOf(node);
} else {
if (getColor(rightOf(rBro)) == BLACK) {
rightRotate(rBro);
rBro = rightOf(parentOf(node));
}
leftRotate(parentOf(node));
setColor(parentOf(node), BLACK);
setColor(rightOf(rBro), BLACK);
break;
}
} else {
RBNode lBro = leftOf(parentOf(node));
if (getColor(lBro) == RED) {
rightRotate(parentOf(node));
lBro = leftOf(node);
}
if (getColor(rightOf(lBro)) == BLACK && getColor(leftOf(lBro)) == BLACK) {
setColor(lBro, RED);
node = parentOf(node);
} else {//Two red or one red
if (getColor(leftOf(lBro)) == BLACK) {
leftRotate(lBro);
lBro = leftOf(parentOf(node));
}
rightRotate(parentOf(node));
setColor(parentOf(node), BLACK);
setColor(leftOf(lBro), BLACK);
break;
}
}
}
setColor(node, BLACK);
}
Complete code and testing
Create TreeMap package
There are three classes under the package:
RBTreeTest
TreeOperation
RBTree
The first two are test classes. If they are written, don't worry. Just run class RBTreeTest
RBTreeTest
package TreeMap;
import java.util.Scanner;
public class RBTreeTest {
public static void main(String[] args) {
//Test that, open that, can't open at the same time
// insertOpt(); // New node
// deleteOpt(); // Delete node
}
public static void insertOpt(){
Scanner scanner=new Scanner(System.in);
RBTree<String,Object> rbt=new RBTree<>();
while (true){
System.out.println("Please enter the node you want to insert:");
String key=scanner.next();
System.out.println();
if(key.length()==1){
key="00"+key;
}else if(key.length()==2){
key="0"+key;
}
rbt.put(key,null);
TreeOperation.show(rbt.getRoot());
}
}
public static void deleteOpt(){
RBTree<String,Object> rbt=new RBTree<>();
rbt.put("001",null);
rbt.put("002",null);
rbt.put("003",null);
rbt.put("004",null);
rbt.put("005",null);
rbt.put("006",null);
rbt.put("007",null);
rbt.put("008",null);
rbt.put("009",null);
rbt.put("010",null);
rbt.put("011",null);
TreeOperation.show(rbt.getRoot());
Scanner scanner=new Scanner(System.in);
while (true){
System.out.println("Please enter the node you want to delete:");
String key=scanner.next();
System.out.println();
if(key.length()==1){
key="00"+key;
}else if(key.length()==2){
key="0"+key;
}
rbt.remove(key);
TreeOperation.show(rbt.getRoot());
}
}
}
TreeOperation
package TreeMap;
public class TreeOperation {
public static int getTreeDepth(RBTree.RBNode root) {
return root == null ? 0 : (1 + Math.max(getTreeDepth(root.getLeft()), getTreeDepth(root.getRight())));
}
private static void writeArray(RBTree.RBNode currNode, int rowIndex, int columnIndex, String[][] res, int treeDepth) {
if (currNode == null) return;
if(currNode.isColor()){
res[rowIndex][columnIndex] = ("\033[30;3m" + currNode.getValue()+"\033[0m") ;
}else {
res[rowIndex][columnIndex] = ("\033[31;3m" + currNode.getValue()+"\033[0m") ;
}
int currLevel = ((rowIndex + 1) / 2);
if (currLevel == treeDepth) return;
int gap = treeDepth - currLevel - 1;
if (currNode.getLeft() != null) {
res[rowIndex + 1][columnIndex - gap] = "/";
writeArray(currNode.getLeft(), rowIndex + 2, columnIndex - gap * 2, res, treeDepth);
}
if (currNode.getRight() != null) {
res[rowIndex + 1][columnIndex + gap] = "\\";
writeArray(currNode.getRight(), rowIndex + 2, columnIndex + gap * 2, res, treeDepth);
}
}
public static void show(RBTree.RBNode root) {
if (root == null) {
System.out.println("EMPTY!");
System.exit(0);
}
int treeDepth = getTreeDepth(root);
int arrayHeight = treeDepth * 2 - 1;
int arrayWidth = (2 << (treeDepth - 2)) * 3 + 1;
String[][] res = new String[arrayHeight][arrayWidth];
for (int i = 0; i < arrayHeight; i ++) {
for (int j = 0; j < arrayWidth; j ++) {
res[i][j] = " ";
}
}
writeArray(root, 0, arrayWidth/2, res, treeDepth);
for (String[] line: res) {
StringBuilder sb = new StringBuilder();
for (int i = 0; i < line.length; i ++) {
sb.append(line[i]);
if (line[i].length() > 1 && i <= line.length - 1) {
i += line[i].length() > 4 ? 2: line[i].length() - 1;
}
}
System.out.println(sb.toString());
}
}
}
RBTree
package TreeMap;
public class RBTree<K extends Comparable<K>,V>{
private RBNode root;
private static final boolean BLACK=true;
private static final boolean RED=false;
public void put(K key,V value){
if(null == root){
root=new RBNode<>(key,value==null?key:value,null);
return;
}
int com;
RBNode tail=root;
RBNode parentTail;
if(key==null){
throw new RuntimeException("Null pointer exception");
}
do{
parentTail=tail;
com=key.compareTo((K) tail.key);
if(com<0){
tail=leftOf(tail);
}else if (com>0){
tail=rightOf(tail);
}else {
tail.value=value==null?key:value;
return;
}
}while (tail!=null);
RBNode newRBNode=new RBNode<>(key,value==null?key:value,parentTail);
if (com<0){
parentTail.left=newRBNode;
}else {
parentTail.right=newRBNode;
}
fixAfterPut(newRBNode);
}
private void fixAfterPut(RBNode newRBNode) {
setColor(newRBNode,RED);
while (newRBNode != root&&getColor(parentOf(newRBNode))==RED){
RBNode grandFather=parentOf(parentOf(newRBNode));
RBNode father=parentOf(newRBNode);
if(leftOf(grandFather)==father){
RBNode uncle=rightOf(grandFather);
if(getColor(uncle)==RED){
setColor(grandFather,RED);
setColor(uncle,BLACK);
setColor(father,BLACK);
newRBNode=grandFather;
}else {
if(rightOf(father)==newRBNode){
leftRotate(father);
newRBNode=father;
}
rightRotate(grandFather);
}
}else {
RBNode uncle=leftOf(grandFather);
if(getColor(uncle)==RED){
setColor(grandFather,RED);
setColor(uncle,BLACK);
setColor(father,BLACK);
newRBNode=grandFather;
}else {
if(leftOf(father)==newRBNode){
rightRotate(father);
newRBNode=father;
}
leftRotate(grandFather);
}
}
}
setColor(root,BLACK);
}
public V remove(K key) {
RBNode node = getNode(key);
if (node == null) {
return null;
}
V oldValue = (V) node.value;
deleteNode(node);
return oldValue;
}
//Get this node
private RBNode getNode(K key) {
RBNode tail = root;
if (root == null) {
throw new RuntimeException("Can't be empty");
}
while (tail != null) {
int cmp = key.compareTo((K) tail.key);
if (cmp < 0) {
tail = leftOf(tail);
} else if (cmp > 0) {
tail = rightOf(tail);
} else {
return tail;
}
}
return null;
}
private RBNode deleteNode(RBNode node) {
if (leftOf(node) != null && rightOf(node) != null) {
RBNode pre = pre(node);
node.key = pre.key;
node.value = pre.value;
node = pre;
}
RBNode replace = leftOf(node) != null ? leftOf(node) : rightOf(node);
if (replace != null) {
replace.parent = parentOf(node);
if (parentOf(node) == null) {
root = replace;
} else if (node == leftOf(parentOf(node))) {
node.parent.left = replace;
} else {
node.parent.right = replace;
}
node.left = node.right = node.parent = null;
if (getColor(node) == BLACK) {
fixAfterRemove(replace);
}
}
else {
if (getColor(node) == BLACK) {
fixAfterRemove(node);
}
if (parentOf(node) != null) {
if (node == leftOf(parentOf(node))) {
node.parent.left = null;
} else {
node.parent.right = null;
}
node.parent = null;
} else {
root = null;
}
}
return null;
}
private void fixAfterRemove(RBNode node) {
while (node != root && getColor(node) == BLACK) {
if (node == leftOf(parentOf(node))) {
RBNode rBro = rightOf(parentOf(node));
if (getColor(rBro) == RED) {
leftRotate(parentOf(node));
rBro = rightOf(parentOf(node));
}
if (getColor(leftOf(rBro)) == BLACK && getColor(rightOf(rBro)) == BLACK) {
setColor(rBro, RED);
node = parentOf(node);
} else {
if (getColor(rightOf(rBro)) == BLACK) {
rightRotate(rBro);
rBro = rightOf(parentOf(node));
}
leftRotate(parentOf(node));
setColor(parentOf(node), BLACK);
setColor(rightOf(rBro), BLACK);
break;
}
} else {
RBNode lBro = leftOf(parentOf(node));
if (getColor(lBro) == RED) {
rightRotate(parentOf(node));
lBro = leftOf(node);
}
if (getColor(rightOf(lBro)) == BLACK && getColor(leftOf(lBro)) == BLACK) {
setColor(lBro, RED);
node = parentOf(node);
} else {
if (getColor(leftOf(lBro)) == BLACK) {
leftRotate(lBro);
lBro = leftOf(parentOf(node));
}
rightRotate(parentOf(node));
setColor(parentOf(node), BLACK);
setColor(leftOf(lBro), BLACK);
break;
}
}
}
setColor(node, BLACK);
}
//precursor
private RBNode pre(RBNode node) {
RBNode l = leftOf(node);
while (l.right != null) {
l = l.right;
}
return l;
}
//Successor
private RBNode suc(RBNode node){
RBNode r=node.right;
while (r.left!=null){
r=r.left;
}
return r;
}
private void leftRotate(RBNode p) {
if(p!=null){
RBNode l=p.right;
setColor(l, p.color);
setColor(p, RED);
p.right = l.left;
if (l.left != null) {
l.left.parent = p;
}
l.parent = p.parent;
if (p.parent == null) {
root = l;
} else if (p.parent.left == p) {
p.parent.left = l;
} else {
p.parent.right = l;
}
l.left = p;
p.parent = l;
}
}
private void rightRotate(RBNode p) {
RBNode r = p.left;
setColor(r, getColor(p));
setColor(p, RED);
p.left = r.right;
if (r.right != null) {
r.right.parent = p;
}
r.parent = p.parent;
if (p.parent == null) {
root = r;
} else if (p.parent.left == p) {
p.parent.left = r;
} else {
p.parent.right = r;
}
r.right = p;
p.parent = r;
}
private static boolean getColor(RBNode rbNode){
return rbNode==null?BLACK:rbNode.color;
}
private static void setColor(RBNode rbNode, boolean b){
if(rbNode!=null){
rbNode.color=b;
}
}
private static RBNode parentOf(RBNode rbNode){
return rbNode==null?null:rbNode.parent;
}
private static RBNode leftOf(RBNode rbNode){
return rbNode==null?null:rbNode.left;
}
private static RBNode rightOf(RBNode rbNode){
return rbNode==null?null:rbNode.right;
}
public void show(){
if(root==null){
System.out.println("empty");
}else {
show(root);
}
}
private void show(RBNode tail){
if (tail.left!=null){
show(tail.left);
}
System.out.println(tail);
if (rightOf(tail)!=null){
show(rightOf(tail));
}
}
public RBNode getRoot() {
return root;
}
static class RBNode<K extends Comparable<K>,V>{
K key;
V value;
private boolean color;
RBNode parent;
RBNode left;
RBNode right;
public RBNode(K key, V value, RBNode parent) {
this.key = key;
this.value = value;
this.color = BLACK;
this.parent = parent;
}
@Override
public String toString() {
return "RBNode{" +
"key=" + key +
", value=" + value +
", color=" + (color?"BLACK":"RED") +
'}';
}
public RBNode getLeft() {
return left;
}
public RBNode getRight() {
return right;
}
public boolean isColor() {
return color;
}
public V getValue() {
return value;
}
}
}