It's not easy to create. The guests come to pay attention to it, collect it and subscribe to it three times at a time❤😜

Preface
Program = data structure + algorithm, algorithm is a mixture of mathematical theory and engineering implementation, is a very interesting and amazing knowledge.Understanding algorithms programming from another perspective will be a new feeling, if you are also learning algorithms, you might as well learn with the director of Mengxin Excellence, take the algorithm!
Catalogue of Series Articles
python daily algorithm | quick sorting with detailed illustrations, tear code by hand!
Summary
This issue introduces the Hill sorting of the Top 10 sorting algorithms. You will learn how to use python for Hill sorting and how to compare the efficiency of Hill sorting with insert sorting and heap sorting.
Catalog
Super python Daily Algorithmic Mind Map
Instance Understanding Hill Sorting
Implementation of Hill Sorting Code
Efficiency comparison of Hill sort, insert sort and heap sort
Time Complexity of Hill Sorting
Super python Daily Algorithmic Mind Map
Shell Sort
What is Hill sorting?
Shell Sort, also known as Decreasing Incremental Sort, is a grouping interpolation sort algorithm.Is a more efficient and improved version of insert ordering.However, Hill sorting is an unstable sorting algorithm.
The basic idea of Hill sorting is to divide the whole sequence of records to be sorted into several subsequences for direct insertion sorting, and then insert and sort all records in sequence directly when the records in the whole sequence are "basically ordered".
More detailed ideas are as follows:
_First take the integers d1=n/2, divide the elements into D1 groups, the distance between adjacent elements is d1, and insert directly into each group to sort;
Take the integer d2=d1/2 and repeat the grouping sorting process until di=1, that is, all elements are directly inserted into the same group to sort.
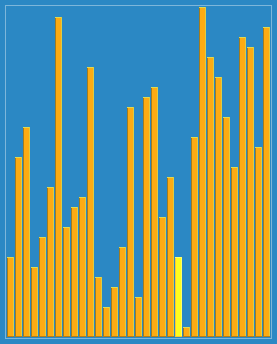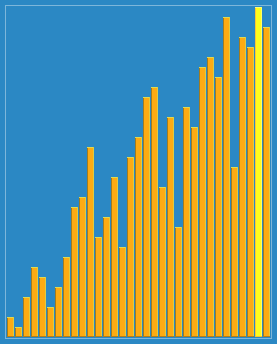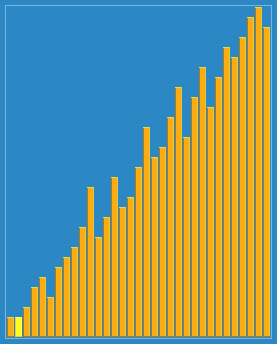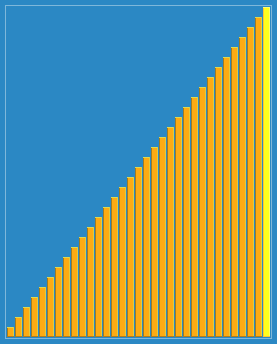
shellsort with gaps 23,10,4,1
Instance Understanding Hill Sorting
For example, we have the following list:
| 5 | 7 | 4 | 6 | 3 | 1 | 2 | 9 | 8 |
We can get d=4 (9//2), so next we'll divide the list into four groups, with four (d) locations separated into one group, so we can divide it into four groups:
| 5 | 3 | 8 |
| 7 | 1 |
| 4 | 2 |
| 6 | 9 |
Next, sort the inserts separately to get the following:
| 3 | 5 | 8 |
| 1 | 7 |
| 2 | 4 |
| 6 | 9 |
Then go back to the original list and get the following list:
| 3 | 1 | 2 | 6 | 5 | 7 | 4 | 9 | 8 |
Next d=d/2=2, divided into two groups, and inserted to sort:
| 2 | 3 | 4 | 5 | 8 |
| 1 | 6 | 7 | 9 |
Then merge:
| 2 | 1 | 3 | 6 | 4 | 7 | 5 | 9 | 8 |
Then d=d/2=1, insert the sort directly:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
This is Hill's sorting process.
Reflection:
Isn't it complicated to think that Hill sorts so many times and invokes insert sorts so many times?
Hill sorting does not order certain elements every time, is to bring the overall data closer and closer to order;Finally, the trip sorting makes all the data ordered.
Implementation of Hill Sorting Code
# Because Hill sort uses the idea of insertion sort, we can change it based on the insertion sort algorithm
def insert_sort_gap(lst,gap): # gap is d, or interval
for i in range(gap,len(lst)): # Start with gap
tmp = lst[i] #
j = i - gap # j stands for the subscript of the card in hand, replaced by Hill sort, then it is compared with the element of gap distance
while lst[j] > tmp and j >= 0:
# Explain lst[i-gap]>lst[i], that is, the case where elements need to be adjusted, such as 3 (lst[i]) and 5 (lst[i-gap]), positions 5>3 and 5 in the instance, 0
lst[j+gap] = lst[j] # So the adjustment is to assign lst[i-gap] to the new lst[i], lst[j+gap], which guarantees that the small rows are ahead and the final output is in ascending order
j -= gap
lst[j+gap] = tmp # lst[j+1] is used to store the cards to be inserted
def shell_sort(lst):
d = len(lst)//2 # Find d d d
while d >= 1: # The final d=1 makes the last loop, so d=1 makes the loop
insert_sort_gap(lst,d) # Sort inserts
d //= 2 # Generate next d
print(lst)
# Detect Hill Sort
lst1 = [i for i in range(14)]
import random
random.shuffle(lst1)
print(f"{lst1}")
shell_sort(lst1)
# Output Results
# [0, 2, 10, 7, 4, 9, 11, 6, 8, 12, 13, 1, 5, 3]
# [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13]Efficiency comparison of Hill sort, insert sort and heap sort
from runtime import * def insert_sort_gap(lst,gap): # gap is d, or interval for i in range(gap,len(lst)): # Start with gap tmp = lst[i] # j = i - gap # j stands for the subscript of the card in hand, replaced by Hill sort, then it is compared with the element of gap distance while lst[j] > tmp and j >= 0: # Explain lst[i-gap]>lst[i], that is, the case where elements need to be adjusted, such as 3 (lst[i]) and 5 (lst[i-gap]), positions 5>3 and 5 in the instance, 0 lst[j+gap] = lst[j] # So the adjustment is to assign lst[i-gap] to the new lst[i], lst[j+gap], which guarantees that the small rows are ahead and the final output is in ascending order j -= gap lst[j+gap] = tmp # lst[j+1] is used to store the cards to be inserted @runtime # Call decorator to calculate Hill sort time def shell_sort(lst): d = len(lst)//2 # Find d d d while d >= 1: # The final d=1 makes the last loop, so d=1 makes the loop insert_sort_gap(lst,d) # Sort inserts d //= 2 # Generate next d # Insert Sort @runtime # Call decorator to calculate insert sort time def insert_sort(lst): for i in range(1,len(lst)): # i denotes the subscript of the touched card tmp = lst[i] # tmp stands for the cards touched j = i - 1 # j stands for the subscript of the card in hand, which automatically has the first card in hand while lst[j] > tmp and j >= 0: # Need to move ordered blocks lst[j+1] = lst[j] j -= 1 lst[j+1] = tmp # lst[j+1] is used to store the cards to be inserted # Heap Sorting def shift(lst,low,high): # low: the position of the root node;high: the position of the last element in the heap i = low # Mark low j = 2 * i + 1 # j stands for left child position tmp = lst[low] # Store the top of the heap while j <= high: # Loop as long as there are elements in the j position if j + 1 <= high and lst[j+1] > lst[j]: # First determine if the j layer has a right child (another number of straight j+1), then the size of the j layer element. If j+1 (having children) is greater than j, J points to j+1 j = j + 1 # j Points to having children if lst[j] > tmp: # Then determine the size of J and the top of the heap element (tmp). If the j position element is larger than the top of the heap element, the top of the heap element and the J (left child) position are interchanged lst[i] = lst[j] i = j # Go on to the next level j = 2 * i + 1 else: # tmp max, put tmp at i lst[i] = tmp # Put tmp at a level break else: lst[i] = tmp # Place tmp on leaf nodes # Heap Sort Primary Function @runtime # Decorator calculates heap sorting time def heap_sort(lst): n = len(lst) # Get List Length for i in range((n-2)//2,-1,-1): # i stands for the subscript of the root of the adjustment section when building a heap, (n-2)//2 is the get position, n-1 is the subscript of the child node, (n-1-1)//2 for the subscript of the root node shift(lst,i,n-1) # i is the top of the heap, high is the last node # Heap building complete for i in range(n-1,-1,-1): # i points to the last node lst[0],lst[i] = lst[i],lst[0] # The top heap element lst[0] is interchanged with the last node location shift(lst,0,i - 1) # i - 1 for the new high # return lst # Inspection efficiency lst1 = [i for i in range(10000)] import random,copy random.shuffle(lst1) lst1_1 = copy.deepcopy(lst1) lst1_2 = copy.deepcopy(lst1) lst1_3 = copy.deepcopy(lst1) shell_sort(lst1_1) insert_sort(lst1_2) heap_sort(lst1_3) # Output Results # shell_sort execution time 0.058002471923828125s # insert_sort execution time 8.6656973361969s # heap_sort execution time 0.08600521087646484s
Time Complexity of Hill Sorting
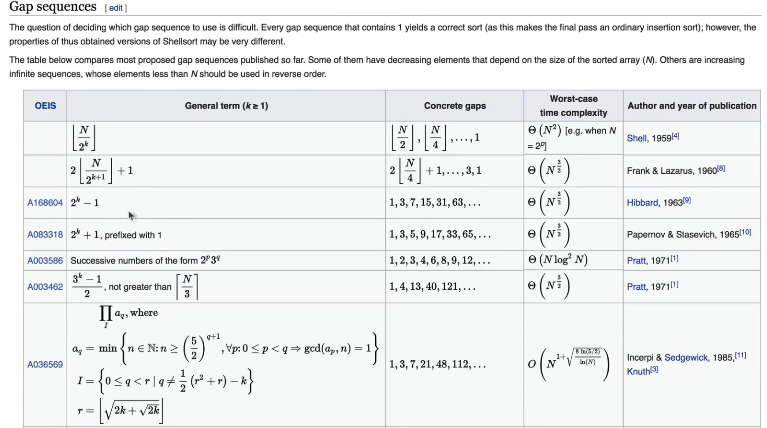
The time complexity of Hill ordering is discussed_More complex and related to the selected gap sequence, there are a lot of big guys studying the calculation of time complexity of gap values with different Hill ordering.
Super power is limited, so you are interested to explore!
It's not easy to create. Let's have a comment!Super Chao goes with you❤😜