Reference notes
https://github.com/PariseC/Algorithms_for_solving_VRP

1. Applicable scenarios

• Solve CVRP
• Single vehicle type
• The vehicle capacity shall not be less than the maximum demand of the demand node
• Single vehicle base

2. Problem analysis

The solution of CVRP problem is a set of paths of multiple vehicles that meet the needs of demand nodes.

Assuming that there are 10 customer nodes in a physical network, numbered 1 ~ 10, and a vehicle base, numbered 0, a feasible solution to this problem can be expressed as: [0-1-2-0,0-3-4-5-0,0-6-7-8-0,0-9-10-0], that is, four vehicles are required to provide services, and the driving routes of vehicles are 0-1-2-0,0-3-4-5-0,0-6-7-8-0 respectively, 0-9-10-0.

Since the capacity of vehicles is fixed and the base is fixed, the solution of the above problem can be expressed as an ordered sequence of [1-2-3-4-5-6-7-8-9-10], and then the sequence can be cut according to the capacity constraints of vehicles to obtain the driving routes of several vehicles. Therefore, the CVRP problem can be transformed into a TSP problem for solution. After obtaining the optimal solution of the TSP problem, the path cutting is carried out considering the vehicle capacity constraint to obtain the solution of the CVRP problem. Such a treatment may affect the quality of the solution of the CVRP problem, but it simplifies the difficulty of solving the problem.

3. Data format

The network data is stored in xlsx file, in which the first line is the title bar and the second line stores the depot data. In the program, vehicle base seq_ The no number is - 1, and the demand node seq_id is numbered from 0. Refer to the relevant documents on the github home page.

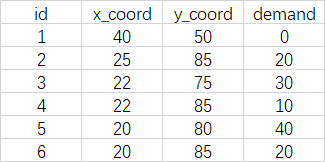
4. Step by step implementation

(1) Data structure

To facilitate data processing, Sol() class, Node() class and Model() class are defined. Their properties are shown in the following table:

• Sol() class, representing a feasible solution

attribute	describe
nodes_seq	Demand node seq_no ordered permutation set, corresponding to the solution of TSP
obj	Optimization target value
routes	Vehicle path set, corresponding to the solution of CVRP

• Node() class, representing a network node

attribute	describe
id	Physical node id, optional
name	Physical node name, optional
seq_no	Physical node mapping id, base node is - 1, and demand node is numbered from 0
x_coord	Physical node x coordinate
y_coord	Physical node y coordinate
demand	Physical node requirements

• The Model() class stores algorithm parameters

attribute	describe
best_sol	Global optimal solution, value type is Sol()
node_list	Physical node collection with value type Node()
node_seq_no_list	Set of physical node mapping IDS
depot	Depot, the value type is Node()
number_of_nodes	Number of demand nodes
opt_type	Optimization target type, 0: minimum number of vehicles, 1: minimum driving distance
vehicle_cap	Vehicle capacity
distance	Network arc distance
rand_d_max	Upper limit of random failure degree
rand_d_min	Lower limit of random failure degree
worst_d_max	Upper limit of worst damage
worst_d_min	Lower limit of worst failure degree
regret_n	Number of suboptimal positions
r1	Operator reward 1
r2	Operator reward 2
r3	Operator reward 3
rho	Operator weight attenuation coefficient
d_weight	Destruction operator weight
d_select	Number of times destruction operator is selected / round
d_score	Damage operator is rewarded with score / round
d_history_select	Total number of times destruction operator history is selected
d_history_score	Total awarded score of destruction operator history
r_weight	Repair operator weight
r_select	Repair operator selected times / round
r_score	The repair operator is rewarded with a score / round
r_history_select	Total number of times repair operator history is selected
r_history_score	Total awarded score of repair operator history

(2) File reading

def readXlsxFile(filepath,model):
    # It is recommended that the vehicle depot data be placed in the first line of xlsx file
    node_seq_no = -1#the depot node seq_no is -1,and demand node seq_no is 0,1,2,...
    df = pd.read_excel(filepath)
    for i in range(df.shape[0]):
        node=Node()
        node.id=node_seq_no
        node.seq_no=node_seq_no
        node.x_coord= df['x_coord'][i]
        node.y_coord= df['y_coord'][i]
        node.demand=df['demand'][i]
        if df['demand'][i] == 0:
            model.depot=node
        else:
            model.node_list.append(node)
            model.node_seq_no_list.append(node_seq_no)
        try:
            node.name=df['name'][i]
        except:
            pass
        try:
            node.id=df['id'][i]
        except:
            pass
        node_seq_no=node_seq_no+1
    model.number_of_nodes=len(model.node_list)

(3) Initialization parameters

The network arc distance is calculated when initializing parameters for use by subsequent operators.

def initParam(model):
    for i in range(model.number_of_nodes):
        for j in range(i+1,model.number_of_nodes):
            d=math.sqrt((model.node_list[i].x_coord-model.node_list[j].x_coord)**2+
                        (model.node_list[i].y_coord-model.node_list[j].y_coord)**2)
            model.distance[i,j]=d
            model.distance[j,i]=d

(4) Initial solution

def genInitialSol(node_seq):
    node_seq=copy.deepcopy(node_seq)
    random.seed(0)
    random.shuffle(node_seq)
    return node_seq

(5) Target value calculation

The target value calculation depends on the "splitRoutes" function to segment the TSP feasible solution to obtain the vehicle driving route and the number of vehicles required, and the "calDistance" function calculates the driving distance.

def splitRoutes(nodes_seq,model):
    num_vehicle = 0
    vehicle_routes = []
    route = []
    remained_cap = model.vehicle_cap
    for node_no in nodes_seq:
        if remained_cap - model.node_list[node_no].demand >= 0:
            route.append(node_no)
            remained_cap = remained_cap - model.node_list[node_no].demand
        else:
            vehicle_routes.append(route)
            route = [node_no]
            num_vehicle = num_vehicle + 1
            remained_cap =model.vehicle_cap - model.node_list[node_no].demand
    vehicle_routes.append(route)
    return num_vehicle,vehicle_routes
def calDistance(route,model):
    distance=0
    depot=model.depot
    for i in range(len(route)-1):
        distance+=model.distance[route[i],route[i+1]]
    first_node=model.node_list[route[0]]
    last_node=model.node_list[route[-1]]
    distance+=math.sqrt((depot.x_coord-first_node.x_coord)**2+(depot.y_coord-first_node.y_coord)**2)
    distance+=math.sqrt((depot.x_coord-last_node.x_coord)**2+(depot.y_coord - last_node.y_coord)**2)
    return distance
def calObj(nodes_seq,model):
    num_vehicle, vehicle_routes = splitRoutes(nodes_seq, model)
    if model.opt_type==0:
        return num_vehicle,vehicle_routes
    else:
        distance=0
        for route in vehicle_routes:
            distance+=calDistance(route,model)
        return distance,vehicle_routes

(6) Define destroy operator (destroy operator)

Two types of destruction are implemented here:

• random destroy: randomly remove a certain proportion of demand nodes from the current solution
• worst destroy: remove a certain proportion of demand nodes from the current solution that cause a large increase in the objective function

# define random destory action
def createRandomDestory(model):
    d=random.uniform(model.rand_d_min,model.rand_d_max)
    reomve_list=random.sample(range(model.number_of_nodes),int(d*model.number_of_nodes))
    return reomve_list
# define worse destory action
def createWorseDestory(model,sol):
    deta_f=[]
    for node_no in sol.nodes_seq:
        nodes_seq_=copy.deepcopy(sol.nodes_seq)
        nodes_seq_.remove(node_no)
        obj,vehicle_routes=calObj(nodes_seq_,model)
        deta_f.append(sol.obj-obj)
    sorted_id = sorted(range(len(deta_f)), key=lambda k: deta_f[k], reverse=True)
    d=random.randint(model.worst_d_min,model.worst_d_max)
    remove_list=sorted_id[:d]
    return remove_list

(7) Define repair operator (repair operator)

Three types of repair are implemented here:

• random repair: randomly insert the removed demand node into the allocated node sequence;
• Green repair: according to the increment size of the objective function of each possible position in the sequence of Allocated Nodes inserted by the removed demand node, select the demand node with the smallest increment of the objective function and the insertion position in turn until all the removed demand nodes are re inserted (which can be simply understood as, Select the demand node that minimizes the increment of the objective function and its optimal insertion position in turn);
  
  Among them, P P P is the unassigned demand node set, I P IP IP is a collection of locations that may be inserted, f ( s p , i ) f(s_{p,i}) f(sp,i) is the demand node p p p insert s s s i i Objective function value at i positions.
• regret repair: calculate the sum of the difference between the objective function value and the objective function value of the optimal position when the removed node is inserted back to n suboptimal positions in the allocated node sequence, and then select the demand node with the largest difference and its optimal position( It can be simply understood that n suboptimal locations and demand nodes far from the optimal location and their optimal locations are preferred.);
  
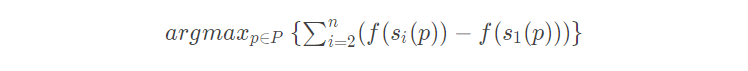
  Among them, P P P is the unassigned demand node set, f ( s i ( p ) ) − f ( s 1 ( p ) ) f(s_{i}(p))-f(s_{1}(p)) f(si (p)) − f(s1 (p)) is the demand node p p p insert s s The optimal position in s and i i i difference of objective function at suboptimal position.

def createRandomRepair(remove_list,model,sol):
    unassigned_nodes_seq=[]
    assigned_nodes_seq = []
    # remove node from current solution
    for i in range(model.number_of_nodes):
        if i in remove_list:
            unassigned_nodes_seq.append(sol.nodes_seq[i])
        else:
            assigned_nodes_seq.append(sol.nodes_seq[i])
    # insert
    for node_no in unassigned_nodes_seq:
        index=random.randint(0,len(assigned_nodes_seq)-1)
        assigned_nodes_seq.insert(index,node_no)
    new_sol=Sol()
    new_sol.nodes_seq=copy.deepcopy(assigned_nodes_seq)
    new_sol.obj,new_sol.routes=calObj(assigned_nodes_seq,model)
    return new_sol

def createGreedyRepair(remove_list,model,sol):
    unassigned_nodes_seq = []
    assigned_nodes_seq = []
    # remove node from current solution
    for i in range(model.number_of_nodes):
        if i in remove_list:
            unassigned_nodes_seq.append(sol.nodes_seq[i])
        else:
            assigned_nodes_seq.append(sol.nodes_seq[i])
    #insert
    while len(unassigned_nodes_seq)>0:
        insert_node_no,insert_index=findGreedyInsert(unassigned_nodes_seq,assigned_nodes_seq,model)
        assigned_nodes_seq.insert(insert_index,insert_node_no)
        unassigned_nodes_seq.remove(insert_node_no)
    new_sol=Sol()
    new_sol.nodes_seq=copy.deepcopy(assigned_nodes_seq)
    new_sol.obj,new_sol.routes=calObj(assigned_nodes_seq,model)
    return new_sol

def findGreedyInsert(unassigned_nodes_seq,assigned_nodes_seq,model):
    best_insert_node_no=None
    best_insert_index = None
    best_insert_cost = float('inf')
    assigned_nodes_seq_obj,_=calObj(assigned_nodes_seq,model)
    for node_no in unassigned_nodes_seq:
        for i in range(len(assigned_nodes_seq)):
            assigned_nodes_seq_ = copy.deepcopy(assigned_nodes_seq)
            assigned_nodes_seq_.insert(i, node_no)
            obj_, _ = calObj(assigned_nodes_seq_, model)
            deta_f = obj_ - assigned_nodes_seq_obj
            if deta_f<best_insert_cost:
                best_insert_index=i
                best_insert_node_no=node_no
                best_insert_cost=deta_f
    return best_insert_node_no,best_insert_index

def createRegretRepair(remove_list,model,sol):
    unassigned_nodes_seq = []
    assigned_nodes_seq = []
    # remove node from current solution
    for i in range(model.number_of_nodes):
        if i in remove_list:
            unassigned_nodes_seq.append(sol.nodes_seq[i])
        else:
            assigned_nodes_seq.append(sol.nodes_seq[i])
    # insert
    while len(unassigned_nodes_seq)>0:
        insert_node_no,insert_index=findRegretInsert(unassigned_nodes_seq,assigned_nodes_seq,model)
        assigned_nodes_seq.insert(insert_index,insert_node_no)
        unassigned_nodes_seq.remove(insert_node_no)
    new_sol = Sol()
    new_sol.nodes_seq = copy.deepcopy(assigned_nodes_seq)
    new_sol.obj, new_sol.routes = calObj(assigned_nodes_seq, model)
    return new_sol

def findRegretInsert(unassigned_nodes_seq,assigned_nodes_seq,model):
    opt_insert_node_no = None
    opt_insert_index = None
    opt_insert_cost = -float('inf')
    for node_no in unassigned_nodes_seq:
        n_insert_cost=np.zeros((len(assigned_nodes_seq),3))
        for i in range(len(assigned_nodes_seq)):
            assigned_nodes_seq_=copy.deepcopy(assigned_nodes_seq)
            assigned_nodes_seq_.insert(i,node_no)
            obj_,_=calObj(assigned_nodes_seq_,model)
            n_insert_cost[i,0]=node_no
            n_insert_cost[i,1]=i
            n_insert_cost[i,2]=obj_
        n_insert_cost= n_insert_cost[n_insert_cost[:, 2].argsort()]
        deta_f=0
        for i in range(1,model.regret_n):
            deta_f=deta_f+n_insert_cost[i,2]-n_insert_cost[0,2]
        if deta_f>opt_insert_cost:
            opt_insert_node_no = int(n_insert_cost[0, 0])
            opt_insert_index=int(n_insert_cost[0,1])
            opt_insert_cost=deta_f
    return opt_insert_node_no,opt_insert_index

(8) Random selection operator

The roulette method is used to select destruction and repair operators.

#select destory action and repair action
def selectDestoryRepair(model):
    d_weight=model.d_weight
    d_cumsumprob = (d_weight / sum(d_weight)).cumsum()
    d_cumsumprob -= np.random.rand()
    destory_id= list(d_cumsumprob > 0).index(True)

    r_weight=model.r_weight
    r_cumsumprob = (r_weight / sum(r_weight)).cumsum()
    r_cumsumprob -= np.random.rand()
    repair_id = list(r_cumsumprob > 0).index(True)
    return destory_id,repair_id

(9) Execute destroy operator

The index sequence of nodes to be removed is returned according to the selected destruction operator.

# do destory action
def doDestory(destory_id,model,sol):
    if destory_id==0:
        reomve_list=createRandomDestory(model)
    else:
        reomve_list=createWorseDestory(model,sol)
    return reomve_list

(10) Execute repair operator

Repair the current connection according to the selected repair operator.

def doRepair(repair_id,reomve_list,model,sol):
    if repair_id==0:
        new_sol=createRandomRepair(reomve_list,model,sol)
    elif repair_id==1:
        new_sol=createGreedyRepair(reomve_list,model,sol)
    else:
        new_sol=createRegretRepair(reomve_list,model,sol)
    return new_sol

(11) Reset operator score

Every pu time destruction and repair are executed, the score of the reset operator and the number of times it is selected.

# reset action score
def resetScore(model):

    model.d_select = np.zeros(2)
    model.d_score = np.zeros(2)

    model.r_select = np.zeros(3)
    model.r_score = np.zeros(3)

(12) Update operator weight

There are two strategies for updating operator weights. One is to update the weights successively every pu time destruction and repair are executed, and the other is to update the weights every time destruction and repair are executed. The former can ensure that the weight is updated in time, but it needs more calculation time; In the latter, by reasonably setting pu parameters, the calculation time is saved, and the weight update does not lag too much. The latter update strategy is adopted here.

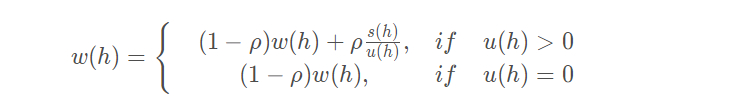
Among them, w ( h ) w(h) w(h) represents the operator weight, ρ ρ ρ Is the attenuation coefficient, s ( h ) s(h) s(h) is the total reward score of the operator, u ( h ) u(h) u(h) is the number of times the operator is selected.

# update action weight
def updateWeight(model):
    for i in range(model.d_weight.shape[0]):
        if model.d_select[i]>0:
            model.d_weight[i]=model.d_weight[i]*(1-model.rho)+model.rho*model.d_score[i]/model.d_select[i]
        else:
            model.d_weight[i] = model.d_weight[i] * (1 - model.rho)
    for i in range(model.r_weight.shape[0]):
        if model.r_select[i]>0:
            model.r_weight[i]=model.r_weight[i]*(1-model.rho)+model.rho*model.r_score[i]/model.r_select[i]
        else:
            model.r_weight[i] = model.r_weight[i] * (1 - model.rho)
    model.d_history_select = model.d_history_select + model.d_select
    model.d_history_score = model.d_history_score + model.d_score
    model.r_history_select = model.r_history_select + model.r_select
    model.r_history_score = model.r_history_score + model.r_score

(13) Draw convergence curve

def plotObj(obj_list):
    plt.rcParams['font.sans-serif'] = ['SimHei']  #show chinese
    plt.rcParams['axes.unicode_minus'] = False   # Show minus sign
    plt.plot(np.arange(1,len(obj_list)+1),obj_list)
    plt.xlabel('Iterations')
    plt.ylabel('Obj Value')
    plt.grid()
    plt.xlim(1,len(obj_list)+1)
    plt.show()

(14) Output results

def outPut(model):
    work=xlsxwriter.Workbook('result.xlsx')
    worksheet=work.add_worksheet()
    worksheet.write(0,0,'opt_type')
    worksheet.write(1,0,'obj')
    if model.opt_type==0:
        worksheet.write(0,1,'number of vehicles')
    else:
        worksheet.write(0, 1, 'drive distance of vehicles')
    worksheet.write(1,1,model.best_sol.obj)
    for row,route in enumerate(model.best_sol.routes):
        worksheet.write(row+2,0,'v'+str(row+1))
        r=[str(i)for i in route]
        worksheet.write(row+2,1, '-'.join(r))
    work.close()

(15) Main function
Two layers of loops are set in the main function. The outer loop is controlled by the epochs parameter and the inner loop is controlled by the pu parameter. The operator weight is updated every time the inner loop is executed. There are many types of acceptance criteria for new neighborhood solutions, such as RW, GRE, SA, Ta, oba and GDA. Here, the TA criterion is adopted, i.e f ( n e w x ) − f ( x ) < T f(newx)-f(x)<T Accept the new solution when f(newx) − f (x) < t, T T T according to coefficient φ φ φ Attenuation, initial T T T is the current solution * 0.2. In addition, when defining the destruction operator, there is no specific damage degree value specified here, but an interval is used to randomly select a damage degree each time to destroy the current solution. For more algorithm details, please refer to reference 1 at the end of the article. For acceleration techniques, please refer to reference 4 and 5 at the end of the article.

def run(filepath,rand_d_max,rand_d_min,worst_d_min,worst_d_max,regret_n,r1,r2,r3,rho,phi,epochs,pu,v_cap,opt_type):
    """
    :param filepath: Xlsx file path
    :param rand_d_max: max degree of random destruction
    :param rand_d_min: min degree of random destruction
    :param worst_d_max: max degree of worst destruction
    :param worst_d_min: min degree of worst destruction
    :param regret_n:  n next cheapest insertions
    :param r1: score if the new solution is the best one found so far.
    :param r2: score if the new solution improves the current solution.
    :param r3: score if the new solution does not improve the current solution, but is accepted.
    :param rho: reaction factor of action weight
    :param phi: the reduction factor of threshold
    :param epochs: Iterations
    :param pu: the frequency of weight adjustment
    :param v_cap: Vehicle capacity
    :param opt_type: Optimization type:0:Minimize the number of vehicles,1:Minimize travel distance
    :return:
    """
    model=Model()
    model.rand_d_max=rand_d_max
    model.rand_d_min=rand_d_min
    model.worst_d_min=worst_d_min
    model.worst_d_max=worst_d_max
    model.regret_n=regret_n
    model.r1=r1
    model.r2=r2
    model.r3=r3
    model.rho=rho
    model.vehicle_cap=v_cap
    model.opt_type=opt_type
    readXlsxFile(filepath, model)
    initParam(model)
    history_best_obj = []
    sol = Sol()
    sol.nodes_seq = genInitialSol(model.node_seq_no_list)
    sol.obj, sol.routes = calObj(sol.nodes_seq, model)
    model.best_sol = copy.deepcopy(sol)
    history_best_obj.append(sol.obj)
    for ep in range(epochs):
        T=sol.obj*0.2
        resetScore(model)
        for k in range(pu):
            destory_id,repair_id=selectDestoryRepair(model)
            model.d_select[destory_id]+=1
            model.r_select[repair_id]+=1
            reomve_list=doDestory(destory_id,model,sol)
            new_sol=doRepair(repair_id,reomve_list,model,sol)
            if new_sol.obj<sol.obj:
                sol=copy.deepcopy(new_sol)
                if new_sol.obj<model.best_sol.obj:
                    model.best_sol=copy.deepcopy(new_sol)
                    model.d_score[destory_id]+=model.r1
                    model.r_score[repair_id]+=model.r1
                else:
                    model.d_score[destory_id]+=model.r2
                    model.r_score[repair_id]+=model.r2
            elif new_sol.obj-sol.obj<T:
                sol=copy.deepcopy(new_sol)
                model.d_score[destory_id] += model.r3
                model.r_score[repair_id] += model.r3
            T=T*phi
            print("%s/%s:%s/%s， best obj: %s" % (ep,epochs,k,pu, model.best_sol.obj))
            history_best_obj.append(model.best_sol.obj)
        updateWeight(model)

    plotObj(history_best_obj)
    outPut(model)
    print("random destory weight is {:.3f}\tselect is {}\tscore is {:.3f}".format(model.d_weight[0],
                                                                        model.d_history_select[0],
                                                                        model.d_history_score[0]))
    print("worse destory weight is {:.3f}\tselect is {}\tscore is {:.3f} ".format(model.d_weight[1],
                                                                        model.d_history_select[1],
                                                                        model.d_history_score[1]))
    print("random repair weight is {:.3f}\tselect is {}\tscore is {:.3f}".format(model.r_weight[0],
                                                                       model.r_history_select[0],
                                                                       model.r_history_score[0]))
    print("greedy repair weight is {:.3f}\tselect is {}\tscore is {:.3f}".format(model.r_weight[1],
                                                                       model.r_history_select[1],
                                                                       model.r_history_score[1]))
    print("regret repair weight is {:.3f}\tselect is {}\tscore is {:.3f}".format(model.r_weight[2],
                                                                       model.r_history_select[2],
                                                                       model.r_history_score[2]))

reference resources

• https://oparu.uniulm.de/xmlui/bitstream/handle/123456789/3264/vts_9568_14474.pdf?sequence=1
• https://homes.di.unimi.it/righini/Didattica/AlgoritmiEuristici/MaterialeAE/15%20-%20ALNS.pdf
• https://mp.weixin.qq.com/s/fpeNCKo62d_7gqBnWd2tTw
• https://mp.weixin.qq.com/s/l7fTHRye4pPBtWrlPrZ6mA
• https://mp.weixin.qq.com/s/K6EgtMdarCgr_vK4qZfGlw https://github.com/PariseC/Algorithms_for_solving_VRP