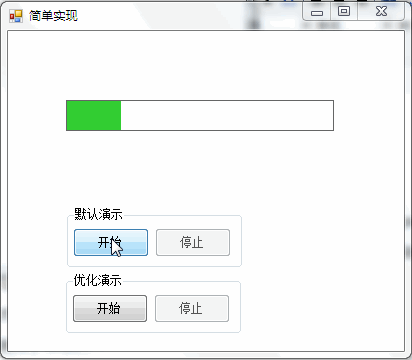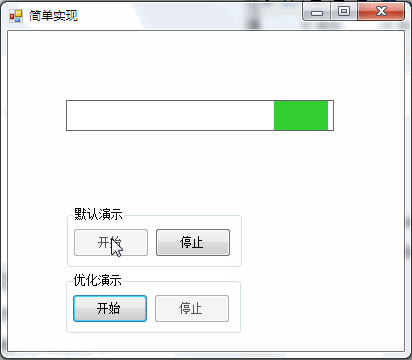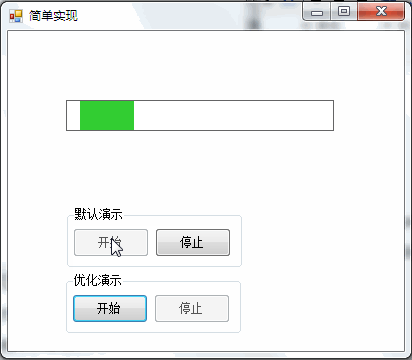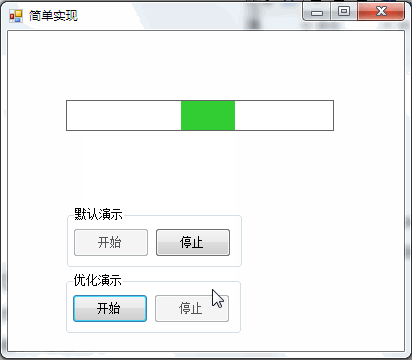
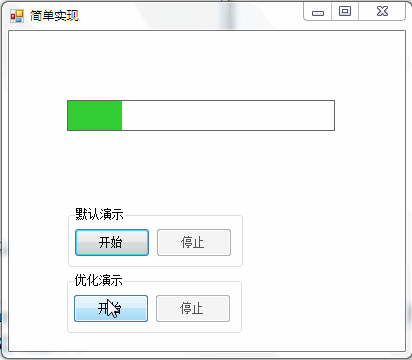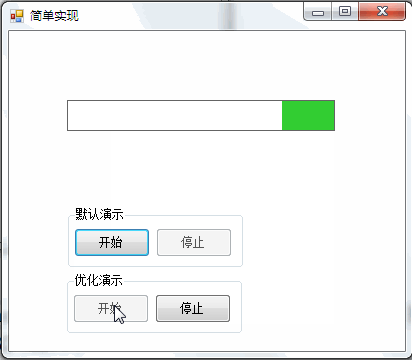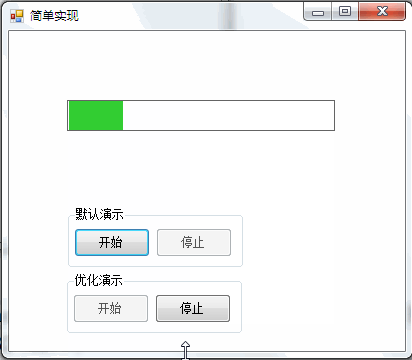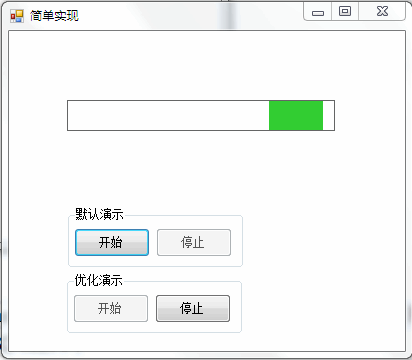
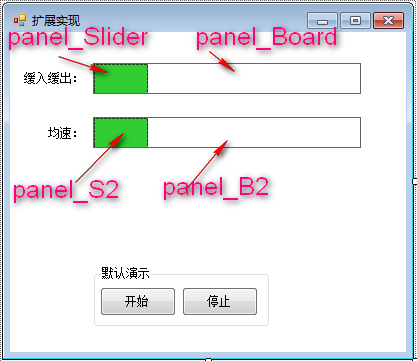
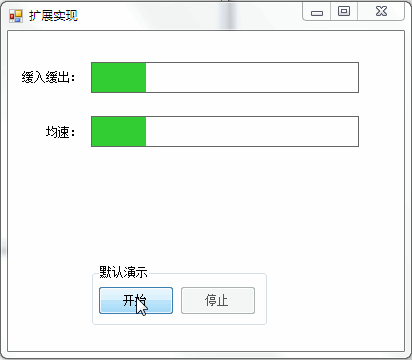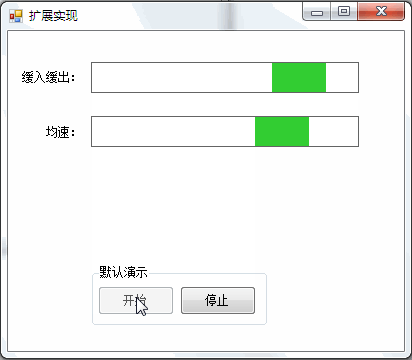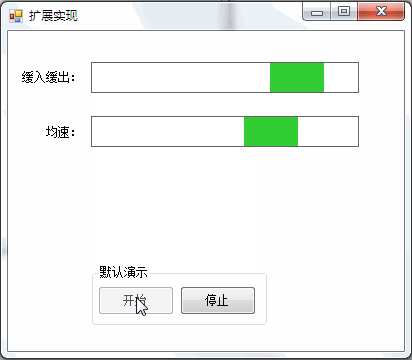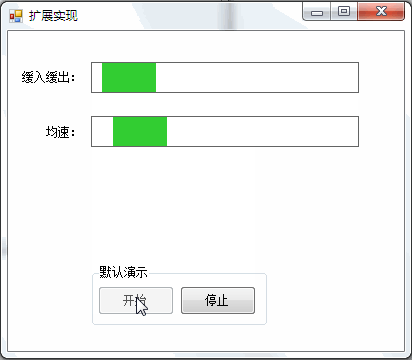
Trigonometric function and slow in and slow out animation and C ා implementation (picture and text explanation)

Keywords: C#

You can often see the animation effect of slow in and slow out, such as:

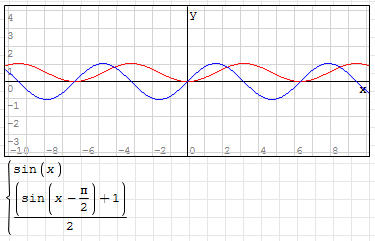
1. Scroll bar with slow in and slow out effect:

2. Breathing lamp with slow in and slow out effect:

Like the above effect, trigonometric function related knowledge is used. Next, we will explain how to achieve this effect step by step from the beginning.

 

 

1, Basic knowledge

(1) Trigonometric function

Commonly used trigonometric functions include sine function (sin), cosine function (cos), tangent function (tan). Sine function and cosine function are commonly used in animation effect. Because they can transform each other, this paper will explain them with sine function.

As shown in the figure below, the right triangle ABC:

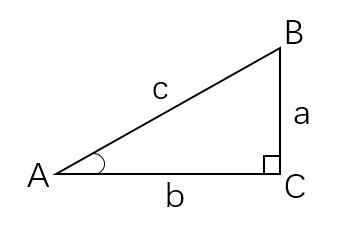
Then:

sin(A)=a/c

That is: sine value of angle A = opposite side / hypotenuse of angle A

(2) Sine curve

The trigonometric function curve is the bridge between trigonometric function and animation.

Taking sine function as an example, its sine curve formula is: y = A*sin(B*x + C) + D

Where y and x are the ordinate and abscissa respectively.

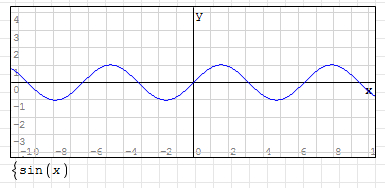
1. In the default state, i.e. y=sin(x), the curve is as follows:

2. The parameter "A" in the sine curve formula controls the amplitude of the curve. The larger the A value is, the larger the amplitude is, the smaller the A value is, and the smaller the amplitude is.

For example: y=2*sin(x), the curve is as shown in the following figure (the blue line is y=sin(x)):

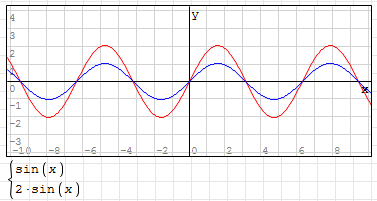
3. The parameter "B" controls the period of the control curve. The larger the value of B, the shorter the period, the smaller the value of B and the longer the period.

For example: y=sin(2x), its curve is shown in the following figure (the blue line is y=sin(x)):

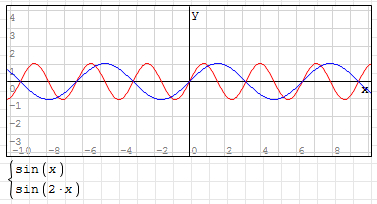
4. The parameter "C" controls the left and right movement of the control curve. The value of C is positive, the curve moves left, the value of C is negative, and the curve moves right;

For example: y=sin(x+1), the curve is as shown in the following figure (the blue line is y=sin(x)):

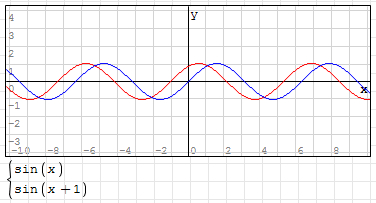
5. The parameter "d" controls the up and down movement of the control curve. D value is positive, curve moves up, D value is negative, curve moves down;

For example: y=sin(x)+1, the curve is as shown in the following figure (the blue line is y=sin(x)):

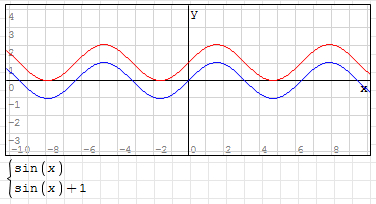
(3) Angle and radian

Because when the code is used to calculate the sine value, the unit is generally radian, like "in C" Math.Sin() "function, but the intuitive effect is angle, so we need to explain the angle and radian.

1. Angle

Definition: two rays are emitted from the center of the circle to the circumference, forming an arc with the included angle and the included angle facing each other. When the arc length is exactly equal to one of 360 minutes of the circumference of the circle, the angle between the two rays is 1 degree.

The schematic diagram is as follows:

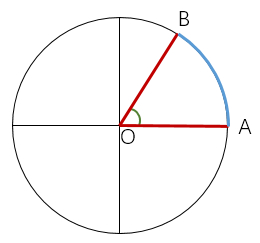
2. Radian

Definition: radian: two rays are emitted from the center of the circle to the circumference, forming an arc with the included angle and the included angle facing each other. When the arc length is exactly equal to the radius of the circle, the angle between the two rays is 1 radian.

The schematic diagram is as follows:

Where: AB=OA=r

3. Difference between angle and radian

The basic difference is that the arc length of the angle is different. Degree is equal to one of the 360 minutes of the circumference of the circle, while arc is equal to the radius.

4. Conversion of angle and radian

Because: arc angle = arc length / radius

So:

a. Circumference (360 °) = circumference / radius = 2 π r/r=2 π

b. Flat angle (180 °) = π

From b, 180 degrees = π radians

So:

c. 1 degree = π / 180 radians (≈ 0.017453 radians)
d. 1 radian = 180 / π degrees (≈ 57.3 degrees)

The conversion formula can be obtained:

Radian = Degree * π / 180
Degree = radian * 180 / π

 

3, Animation implementation

The idea of realization is simply to use the change of "y" and "x" value of sine curve. For slow in and slow out animation, it is the change of speed.

Definition and formula of velocity: the velocity is numerically equal to the ratio of the displacement of the object movement to the time of the displacement. The calculation formula of velocity is v = Δ s / Δ t

Controlling speed is nothing more than the change of distance and time.

In the implementation of applications, it is often not to change two quantities at the same time, but to fix one quantity and change one quantity.

In the actual program implementation, it is usually fixed "time", only changing "distance". Here "time" can be understood as "time interval". That is to say, when the time interval is constant, the running distance within each time interval needs to be considered.

Then the reflection on the sine curve is the value of y under equal x interval.

(1) Simple implementation

(1) Implementation ideas:

1. The curve of y=sin(x) shows that the range of y value is (- 1 ~ + 1)

2. Move the curve up by a distance of 1, i.e. y=sin(x)+1. At this time, the range of y value: (0 ~ 2)

3. To change the range of y value to (0 ~ 1), divide the function by 2, that is, y=(sin(x)+1)/2

As shown in the figure (the blue line is y=sin(x)):

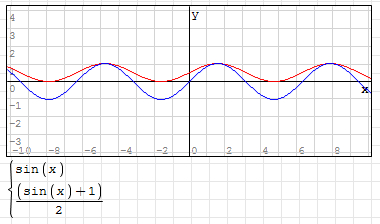
4. Multiply the y value by the swing distance of the slow in and slow out animation

(2) C. implementation:

1. Control layout and properties

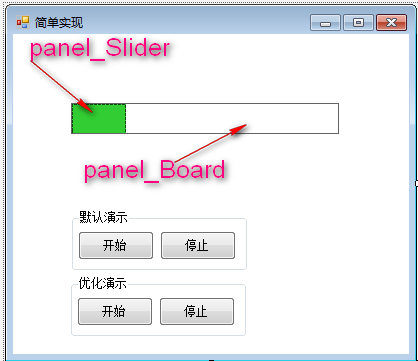
2. Core code

 1 void pShowD()
 2 {
 3     //i It's degrees, not radians
 4     int i = 0;
 5     //To move the distance, subtract the width of the slider itself
 6     double dMoveDistance = panel_Board.Width - panel_Slider.Width;
 7     while (true)
 8     {
 9         i++;
10         if (i > 360)
11         {
12             //One cycle is 360 degrees
13             i = 0;
14         }
15         //Fixed time interval
16         Thread.Sleep(10);
17         //Pass formula: radians=degree*π/180，Degree i Convert to Math.Sin()Number of radians required
18         double dz = dMoveDistance * (1 + Math.Sin(i * Math.PI / 180)) / 2;
19         pSetLeft(Convert.ToInt32(dz));
20 
21     }
22 }
23 
24 void pSetLeft(int i)
25 {
26     if (panel_Slider.InvokeRequired)
27     {
28         panel_Slider.Invoke(new Action<int>(pSetLeft), new object[] { i });
29     }
30     else
31     {
32         panel_Slider.Left = i;
33     }
34 }
Simple implementation

3. Operation effect

(2) Simple optimization

By observing the above implementation, it can be found that although the slow in and slow out effect has been achieved, the "panel" of the_ The starting position of slider) is not the leftmost, but from the middle.

It can also be seen from the above formula that when x=0, y=(sin(x)+1)/2=1/2, that is, one half of the whole swing distance.

(1) Optimization ideas

In order for the slider to start from the far left, you need to move the curve to the right by π / 2.

The curve formula becomes: y=(sin(x - π / 2) + 1) / 2

As shown in the figure (the blue line is y=sin(x)):

(2) C ා implementation

1. The layout is the same as above.

2. Core code

 1 void pShowD2()
 2 {
 3     //i It's degrees, not radians
 4     int i = 0;
 5     //The moving distance subtracts the width of the slider itself
 6     double dMoveDistance = panel_Board.Width - panel_Slider.Width;
 7     while (true)
 8     {
 9         i++;
10         if (i > 360)
11         {
12             //One cycle is 360 degrees
13             i = 0;
14         }
15         //Fixed time interval
16         Thread.Sleep(10);
17         //Pass formula: radians=degree*π/180，Degree i Convert to Math.Sin()Number of radians required
18         //because i It's degrees, so it's( i-90)
19         double dz = dMoveDistance * (1 + Math.Sin((i-90) * Math.PI / 180)) / 2;
20         pSetLeft(Convert.ToInt32(dz));
21 
22     }
23 }
24 
25 void pSetLeft(int i)
26 {
27     if (panel_Slider.InvokeRequired)
28     {
29         panel_Slider.Invoke(new Action<int>(pSetLeft), new object[] { i });
30     }
31     else
32     {
33         panel_Slider.Left = i;
34     }
35 }
Simple implementation (optimization)

3. Operation effect

(3) Extended implementation

In practice, animation often needs to be completed in a fixed time.

Take the previous implementation as an example to fix the time for the slider to slide from the left end to the right end to 1 second. How to achieve it?

(1) implementation ideas

There is no big difference between the whole idea and the previous one. It is still a fixed "time" and a "changing" distance ".

Based on the previous "simple implementation (optimization)", the following modifications and supplements need to be added:

1. If the "time Interval" is: Interval, it will change (Step=1/Interval) times in the specified 1 second.

2. Then, the degree of each change is no longer "1", another cycle is the slider back and forth, so the degree of the second change is: Per=2 π / 2*Step=180/Step.

(2) C ා implementation

In the implementation, the constant speed contrast is added.

1. Layout and properties

2. Core code

 1 void pShowD2()
 2 {
 3     //Current slider position
 4     double d = 0;
 5     //true/false: Slide right/Slide left
 6     bool bToRight = true;
 7     //Time interval, unit: ms
 8     int iInterval = 10;
 9     //Total time required from left to right, unit: ms
10     int iAnimateTime = 1000;
11     //The moving distance subtracts the width of the slider itself
12     double dMoveDistance = panel_Board.Width - panel_Slider.Width;
13     //Number of changes required
14     double dStep = Convert.ToDouble(iAnimateTime) / iInterval;
15     //Increased distance per change
16     double dPerX = dMoveDistance / dStep;
17     while (true)
18     {
19         d = bToRight ? d + dPerX : d - dPerX;
20         if (d > dMoveDistance)
21         {
22             bToRight = false;
23         }
24         if (d < 0)
25         {
26             bToRight = true;
27         }
28 
29         Thread.Sleep(iInterval);
30         int iZ = Convert.ToInt32(d);
31         pSetLeft2(iZ);
32 
33     }
34 }
35 void pSetLeft2(int i)
36 {
37     if (panel_S2.InvokeRequired)
38     {
39         panel_S2.Invoke(new Action<int>(pSetLeft2), new object[] { i });
40     }
41     else
42     {
43         panel_S2.Left = i;
44     }
45 }
1. Uniform speed 
 1 void pShowD()
 2 {
 3     //d It's degrees, not radians
 4     double d = 0;
 5     //Time interval, unit: ms
 6     int iInterval = 10;
 7     //Total time required from left to right, unit: ms
 8     int iAnimateTime = 1000;
 9     //The moving distance subtracts the width of the slider itself
10     double dMoveDistance = panel_Board.Width - panel_Slider.Width;
11     //Number of changes required
12     double dStep = Convert.ToDouble(iAnimateTime) / iInterval;
13     //Degrees increased per change
14     double dPer = 180.0 / dStep;
15     while (true)
16     {
17         d += dPer;
18         if (d > 360)
19         {
20             //One cycle is 360 degrees
21             d = 0;
22         }
23         //Fixed time interval
24         Thread.Sleep(iInterval);
25         //Pass formula: radians=degree*π/180，Degree i Convert to Math.Sin()Number of radians required
26         double dz = dMoveDistance * (1 + Math.Sin((d - 90) * Math.PI / 180)) / 2;
27         pSetLeft(Convert.ToInt32(dz));
28 
29     }
30 }
31 
32 void pSetLeft(int i)
33 {
34     if (panel_Slider.InvokeRequired)
35     {
36         panel_Slider.Invoke(new Action<int>(pSetLeft), new object[] { i });
37     }
38     else
39     {
40         panel_Slider.Left = i;
41     }
42 }
2. Slow in and slow out

3. Operation effect

 

 

4, Conclusion

This article mainly talks about trigonometric function and slow in and slow out animation, but trigonometric function is not only used in animation, such as drawing wave effect by directly using the shape of sine curve - this effect can be used in charging, progress bar and other places.

And knowing the function of curves in animation, we can achieve different animation effects through different function curves, such as another very useful "Bezier curve", which can achieve more complex and elegant animation effects.

 

If there are any mistakes and shortcomings, you are welcome to criticize and correct.

Posted by dunnsearch on Sat, 20 Jun 2020 02:06:21 -0700

Hot Keywords

©2025 Programmer Group