Problem Description:
The largest k-th element was found in the unsorted array. Note that you need to look for the k-th largest element after array sorting, not the k-th different element.
It is one of the questions often asked in interview. At the same time, it is also a good question to investigate the calculation of time complexity due to its numerous solutions.
1. Select Sorting
By using selection sorting, the largest element in the array is placed at the front end of the array, and then the largest element selected for the k-th time is the k-th largest element, and the result can be returned directly according to the index.
public class Select { public static void main(String[] args) { int[] arr = new int[]{5,3,2,1,4,7,8,10,6,9}; System.out.println(findKthLargest(arr, 3)); } private static int findKthLargest(int[] arr, int k){ if(k <= 0 || k > arr.length) throw new IllegalArgumentException("k error"); for(int i = 0; i < k; ++i){ int maxNum = Integer.MIN_VALUE; int maxIndex = -1; for(int j = i; j < arr.length; ++j){ if(arr[j] > maxNum){ maxNum = arr[j]; maxIndex = j; } } swap(arr, maxIndex, i); } System.out.println(Arrays.toString(arr)); return arr[k-1]; } private static void swap(int[] arr, int i, int j){ int temp = arr[i]; arr[i] = arr[j]; arr[j] = temp; } }
Results:
[10, 9, 8, 1, 4, 7, 2, 5, 6, 3] 8
We can see that after the array is sorted, the first three elements are the largest of the three selections, and the elements that directly return the k-1 index position are the K-largest elements.
Time complexity O(n*K), after K times of selection, each selection must traverse n elements.
2. Sorting optimization
The essence of the previous method is actually to sort the whole array, and then get the answer according to the index position. Based on this situation, we can use some faster sorting methods, such as selecting sorting or merging sorting, to achieve a tie time complexity of O(nlogn)
public class Sort { public static void main(String[] args) { int[] arr = new int[]{5,3,2,1,4,7,8,10,6,9}; System.out.println(findKthLargest(arr, 2)); } private static int findKthLargest(int[] arr, int k){ if(k <= 0 || k > arr.length) throw new IllegalArgumentException("k error"); Arrays.sort(arr); System.out.println(Arrays.toString(arr)); return arr[arr.length-k]; } }
Results:
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10] 9
Time complexity O(nlogn). The worst time complexity is different according to different sorting methods. Fast sorting is O(n^2), and merging sorting is O(nlogn).
3. Heap (priority queue)
The idea is to create a minimum heap, add all the elements in the array to the heap, and keep the heap size less than or equal to K. In this way, the first k largest elements remain in the heap. In this way, the element at the top of the heap is the correct answer.
public class Heap { public static void main(String[] args) { int[] arr = new int[]{5,3,2,1,4,7,8,10,6,9}; System.out.println(findKthLargest(arr, 3)); } private static int findKthLargest(int[] arr, int k){ if(k <= 0 || k > arr.length) throw new IllegalArgumentException("k error"); PriorityQueue<Integer> queue = new PriorityQueue<>((a,b)->{ return a-b; }); for(int num:arr){ queue.offer(num); if(queue.size() > k) queue.poll(); } return queue.peek(); } }
The time complexity is O (n logK), the time complexity of adding or deleting elements to the heap of size k is O(logk), traversing n elements, so the total time complexity is O(nlogk)
4. Quick selection
Based on the idea of quick arrangement, select a datum element, and divide the array into two parts. The elements on the left side are larger than the datum elements, and the elements on the right side are smaller than the datum elements. If the index of the datum element is exactly equal to k-1, that is to say, the datum element is the element with the largest K, otherwise, select it on the left or right side according to the position of the datum element.
import java.util.PriorityQueue; import java.util.Random; public class QuickSelect { public static void main(String[] args) { int[] arr = new int[]{5,3,2,1,4,7,8,10,6,9}; System.out.println(findKthLargest(arr, 10)); } private static int findKthLargest(int[] arr, int k){ if(k <= 0 || k > arr.length) throw new IllegalArgumentException("k error"); return quickSelect(arr, 0, arr.length-1, k); } private static int quickSelect(int[] arr, int left, int right, int k){ if(left == right) return arr[left]; Random random_num = new Random(); int pivotIndex = left + random_num.nextInt(right - left); pivotIndex = partition(arr, left, right, pivotIndex); if(pivotIndex == k-1){ return arr[pivotIndex]; }else if(pivotIndex < k-1){ return quickSelect(arr, pivotIndex+1, right, k); }else{ return quickSelect(arr, left, pivotIndex-1, k); } } private static int partition(int[] arr, int left, int right, int pivotIndex){ int pivot = arr[pivotIndex]; swap(arr, pivotIndex, right); int l = left, r = right; while(l < r){ while(l < r && arr[l] >= pivot) l++; if(arr[l] < pivot) swap(arr, l, r); while(l < r && arr[r] <= pivot) r--; if(arr[r] > pivot) swap(arr, l, r); } return l; } private static void swap(int[] arr, int i, int j){ int temp = arr[i]; arr[i] = arr[j]; arr[j] = temp; } }
Here we choose the random value in an array as the reference value. If every time exactly half of the elements are divided, then t (n) = n + n / 2 + n / 4 + n / 8 + n / 16 +... = 2n, that is, the time complexity of O(n).
However, if each selected element is exactly the minimum value, the time complexity will be reduced to O(n^2)
However, the average time complexity is O(n), which is strictly proved in the introduction of the algorithm.
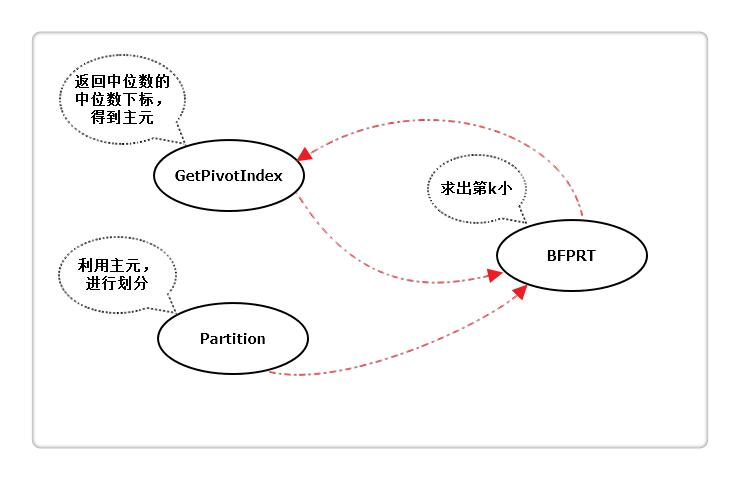
5,BFPRT
In BFPRT algorithm, we only change the selection of pivot value in the quick sorting section. In the quick sorting, we always choose the first or last element as pivot, while in BFPTR algorithm, we choose the median of the quintile as pivot every time, so as to make the division more reasonable and avoid the worst-case. The algorithm steps are as follows:
- Divide the n elements of the input array into n/5 groups with 5 elements in each group, and at most one group consists of the remaining n%5 elements.
- Find the median of each group in n/5 groups, first insert and sort the elements of each group, and then select the median from the sorted sequence.
- For the n/5 median found in 2, recursively carry out steps 1 and 2 until only one number is left, that is, the median of the n/5 elements. After finding the median, find the corresponding subscript p.
- In the partition process, the pivot element subscript in the partition is p.
- Just judge the high and low areas
The worst-case time complexity of the algorithm is O(n). It is worth noting that the array is divided into two parts according to the K-small (large) elements by BFPTR algorithm, and the high and low parts are not necessarily orderly. Generally, we do not need to find out the order, but only need to find the K-large or K-small.
public class BFPRT { public static void main(String[] args) { int[] arr = new int[]{3,2,3,1,2,4,5,5,6}; System.out.println(findKthLargest(arr, 4)); } private static int findKthLargest(int[] arr, int k){ if(k <= 0 || k > arr.length) throw new IllegalArgumentException("k error"); return quickSelect(arr, 0, arr.length-1, k); } private static int findMedian(int[] arr, int l, int r){ int i = l, index = 0; for(; i + 4 <= r; i += 5, index++){ sort(arr, i, i + 4); swap(arr, l + index, i + 2); } if(i <= r){ sort(arr, i, r); swap(arr, l+index, i + (r-i+1) / 2); //If the last array element is even, choose the smaller one index++; } if(index == 1) return l; else return findMedian(arr, l, l+index-1); } private static int quickSelect(int[] arr, int left, int right, int k){ if(left == right) return arr[left]; // Random random = new Random(); // int pivotIndex = left + random.nextInt(right - left); int pivotIndex = findMedian(arr, left, right); pivotIndex = partition(arr, left, right, pivotIndex); if(pivotIndex == k-1){ return arr[pivotIndex]; }else if(pivotIndex < k-1){ return quickSelect(arr, pivotIndex+1, right, k); }else{ return quickSelect(arr, left, pivotIndex-1, k); } } private static int partition(int[] arr, int left, int right, int pivotIndex){ int pivot = arr[pivotIndex]; swap(arr, pivotIndex, right); int l = left, r = right; while(l < r){ while(l < r && arr[l] >= pivot) l++; if(arr[l] < pivot) swap(arr, l, r); while(l < r && arr[r] <= pivot) r--; if(arr[r] > pivot) swap(arr, l, r); } return l; } private static void swap(int[] arr, int i, int j){ int temp = arr[i]; arr[i] = arr[j]; arr[j] = temp; } public static void sort(int[] arr, int l, int r){ for(int i = l; i <= r; i++){ for(int j = i+1; j <= r; j++){ if(arr[j] < arr[i]) swap(arr, i, j); } } } }