Maximum spacing

1. Title

Given an unordered array, find out the maximum difference between adjacent elements after sorting.
Returns 0 if the number of array elements is less than 2.

Example 1

Example 2

explain:

• You can assume that all elements in an array are non negative integers and that the values are in the 32-bit signed integer range.
• Please try to solve this problem under the condition of linear time complexity and space complexity.

Topic template

/**
 * @param {number[]} nums
 * @return {number}
 */
var maximumGap = function(nums) {

};

2. Thought analysis

Traditional method: sort first, then traverse again, and find the maximum difference in the process of traversal
After upgrade: find the maximum difference during sorting

3. Methods used

See explanation

4. Problem solving and optimization

Traditional approach:

let maximumGap = (nums) => {
  let maxGap = 0
  if (nums.length < 2) return maxGap
  // sort
  for (let i = nums.length - 1; i > 0; i--) {
    for (let j = 0; j < i; j++) {
      [nums[j], nums[j + 1]] = nums[j] > nums[j + 1] ? [nums[j + 1], nums[j]] : [nums[j], nums[j + 1]]
    }
  }
  nums.reduce((pre, cur) => {
    maxGap = cur - pre > maxGap ? cur - pre : maxGap
    return cur
  })
  return maxGap
}

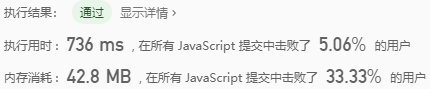
Cache maximum spacing during sorting:

  let maxGap = 0
  if (nums.length < 2) return maxGap
  if (nums.length === 2) return nums[1] - nums[0] > maxGap ? nums[1] - nums[0] : maxGap
  // sort
  for (let i = nums.length - 1; i > 0; i--) {
    for (let j = 0; j < i; j++) {
      [nums[j], nums[j + 1]] = nums[j] > nums[j + 1] ? [nums[j + 1], nums[j]] : [nums[j], nums[j + 1]]
    }
    if (i < nums.length - 1) maxGap = nums[i + 1] - nums[i] > maxGap ? nums[i + 1] - nums[i] : maxGap
  }
  return maxGap

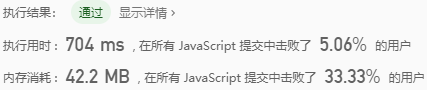
The result was not satisfactory

Use cardinality sort

let maximumGap = (nums) => {
  let maxGap = 0
  if (nums.length < 2) return maxGap

  let mod = 10 // Base / radix, usually with Radix as variable name
  let dev = 1 // It is used to get the base data
  let maxDigit = Math.max(...nums).toString().length // Maximum number of digits
  let counter = []
  for (let i = 0; i < maxDigit; i++, dev *= 10, mod *= 10) {
    for (let j = 0; j < nums.length; j++) {
      // Extract the data of the corresponding base bit (bits / tens / hundreds...), which is equivalent to the number of buckets sorted
      let bucket = Math.floor((nums[j] % mod) / dev)
      // Initialize statistics array
      if (counter[bucket] == null) {
        counter[bucket] = []
      }
      // Corresponding to group joining (this is equivalent to sorting), use LSD (secondary priority) to sort the cardinality
      counter[bucket].push(nums[j])
    }
    let pos = 0
    for (let j = 0; j < counter.length; j++) {
      let value = null
      if (counter[j] != null) {
        while ((value = counter[j].shift()) != null) {
          nums[pos++] = value
        }
      }
    }
    // console.log('nums', nums) / / here you can get the results sorted by bit, ten bit
  }
  nums.reduce((pre, cur) => {
    maxGap = cur - pre > maxGap ? cur - pre : maxGap
    return cur
  })
  return maxGap
}

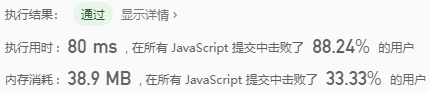
Not bad

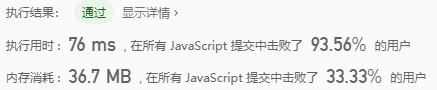
Combined with barrel sorting and pigeon cage principle:

let maximumGap = (nums) => {
  if (nums.length < 2) return 0
  let min = Math.min(...nums) // minimum value
  let max = Math.max(...nums) // Maximum
  if (max - min === 0) return 0
  let gap = Math.ceil((max - min) / (nums.length - 1)) // Average difference (the average value of the two differences is rounded down)
  // Lower limit of barrel (interval) and upper limit of barrel (interval) (the purpose of filling is to skip empty barrel (interval))
  let bucketsMin = new Array(nums.length - 1).fill(max) // Number.MAX_SAFE_INTEGER
  let bucketsMax = new Array(nums.length - 1).fill(min)
  for (let i = 0; i < nums.length; i++) {
    if (nums[i] === min || nums[i] === max) continue // Maximum and minimum two values are not allowed in the barrel
    let idx = Math.floor((nums[i] - min) / gap) // Positioning the correct barrel
    // Core steps: only the upper and lower limits of the bucket (interval) are left in the statistical process, and other unrelated intermediate elements are removed (the maximum spacing must be greater than the average difference, and it must be generated between the differences of the edge values)
    bucketsMin[idx] = Math.min(nums[i], bucketsMin[idx]) // Lower limit of statistical barrel (interval)
    bucketsMax[idx] = Math.max(nums[i], bucketsMax[idx]) // Upper limit of statistical barrel (interval)
  }
  let maxGap = 0 // Storage maximum interval
  let pre = min
  for (let i = 0; i < nums.length - 1; i++) {
    if (bucketsMax[i] === min) continue // Skip empty bucket (interval)
    // Core step: count the maximum value of the difference between the edge values (another step is outside the loop)
    maxGap = Math.max(maxGap, bucketsMin[i] - pre) // The maximum value of the difference between the lower limit of this interval and the upper limit of the previous interval (the difference between the lower limit of the first interval and the minimum value is also under comparison)
    pre = bucketsMax[i]
  }
  maxGap = Math.max(maxGap, max - pre) // Finally, the difference between the lower limit and the maximum value of a non empty interval is also included in the comparison
  return maxGap
}

Suppose there is a bucket for any element in the array, then each element occupies exactly one bucket. Now, if we increase the number of buckets, there must be at least one bucket that is empty. Then the difference between the two elements near the empty bucket is the result we want

In the code, two maximums are placed in the bucket on the two sides, and the number of array elements is - 1 bucket. During the process of element entering the bucket, there will be multiple elements entering a bucket. Therefore, only the maximum and minimum values (upper and lower limits of the interval) belonging to the bucket are placed in the bucket, and then the process of finding the empty bucket is as follows:

• The maximum value of the difference between the lower limit of this interval and the upper limit of the previous interval (the empty interval is omitted)
• The difference between the lower limit of the first interval and the minimum value is also under comparison
• Finally, the difference between the lower limit and the maximum value of a non empty interval is also included in the comparison

It can be understood that the maximum interval must be greater than the average interval ((max − min)/(n − 1)(max-min)/(n-1)(max − min)/(n − 1)), and the average interval is the capacity of the barrel.

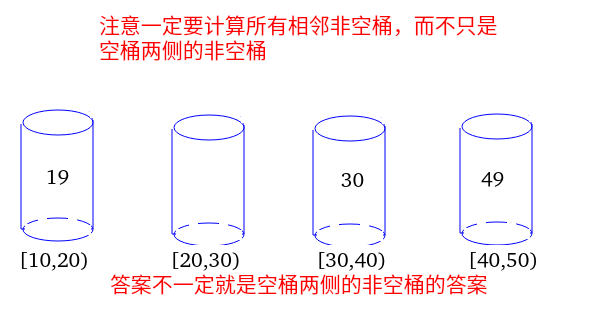
Image from: Leetcode-164.maximumgap (maximum spacing)
-----—