1, Background

Divide and conquer algorithm is one of the five algorithms commonly used in computer, and also one of the algorithms often used in JAVA programming. For the understanding of divide and conquer algorithm, often stay in some boring concepts, such as "divide and conquer", "problem atomic decomposition", etc. This paper will start with a number guessing game, and lead to the thinking of the basic idea of divide and conquer algorithm.

2, Figure guessing game

2.1 rules of the game

• Generate a random integer between [1-100] by computer;
• Human beings can only guess one number per round;
• The computer feeds back on the numbers given by humans:
  --If the number given by human is larger than that given by computer, the feedback is "larger than this number";
  --If the number given by human is smaller than that given by computer, the feedback is "smaller than this number";
  --If the number given by human is equal to that given by computer, the feedback is "guessed".
• Unlimited number of guesses, whichever is right

2.2 guess the source code of digital game

• According to the rules of the game, we first form the code:

/**
 * Figure guessing game
 *
 * @author zhuhuix
 * @date 2020-06-11
 */
public class Guess {

    public static void main(String[] args) throws IOException {
        int num = generateRandomInteger(1, 100);
        int guessNum = 0;
        BufferedReader bufferedReader = new BufferedReader(new InputStreamReader(System.in));
        System.out.println("A [1] has been generated-100]Please start to guess...");
        while (num != guessNum) {

            String s = bufferedReader.readLine();
            if (!s.matches("[0-9]+")) {
                System.out.println("Please enter an integer..");
                continue;
            }
            guessNum=Integer.parseInt(s);
            if (guessNum > 100 || guessNum < 1) {
                System.out.println("Please enter a [1-100]integer..");
                continue;
            }
            if (guessNum<num){
                System.out.println("Sorry,It's bigger than that. Please continue...");
            }
            if (guessNum>num){
                System.out.println("Sorry,It's smaller than this number. Please continue...");
            }

        }

        System.out.println("Congratulations, you guessed it!!!");

    }

    /**
     * Generate a random number within the specified range
     *
     * @param left  Start number
     * @param right Termination number
     * @return random number
     */
    private static int generateRandomInteger(int left, int right) {
        Random random = new Random();
        return left + random.nextInt(right - left + 1);
    }
}

2.3 number guessing skills

• Let's see how humans guess:
  --Do you find any rules?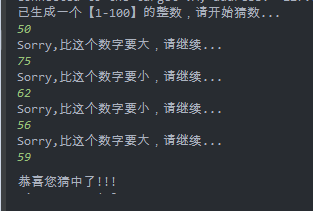
  
• The skill of human guessing numbers:
  --Guess the median of 50,
  --Split the digital range in half according to the computer's "large" or "small" feedback
  --Repeat the above decomposition process until the corresponding number is found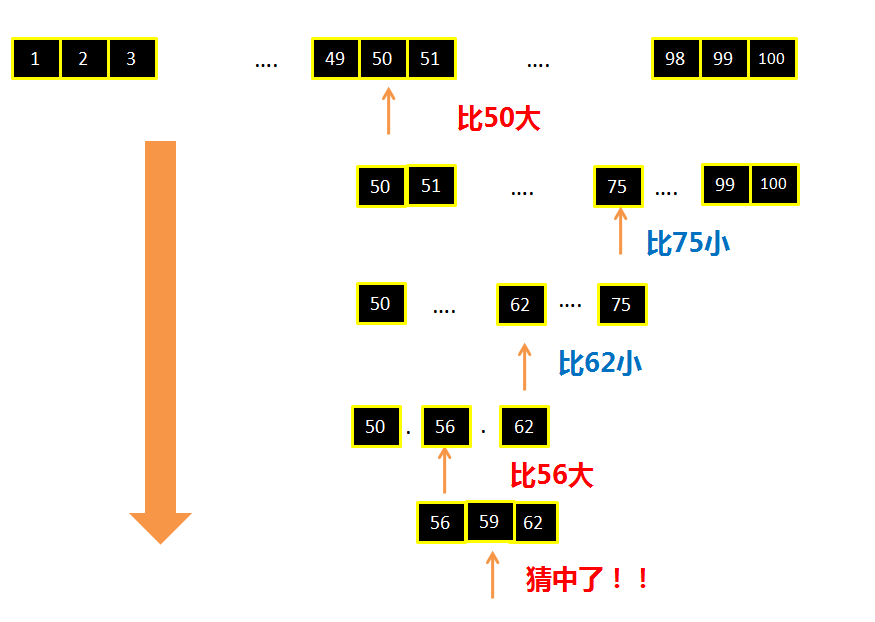
  

3, Divide and conquer algorithm

3.1 ideas and Strategies

• Note: it's the same problem. Just like the number guessing game, the original problem is the number of [1-100], divided into [1-49], [50-100], [50-75]... These numbers have reduced the scale, and the nature of the problem has never changed.

3.2 applicable characteristics

• If the problem is reduced to a certain scale, it will be easy to solve: for example, if the number range of the number guessing game is reduced from [1-100] to [56-62], it will be easy to guess.
• The sub problems formed after the reduction of the scale of the problem are independent of each other.
• No matter how small the scale of the problem is, its nature cannot be changed.
• The solution of the subproblem decomposed by the problem can be combined into the solution of the problem

3.3 typical application of divide and conquer algorithm

3.3.1 principle of merging and sorting

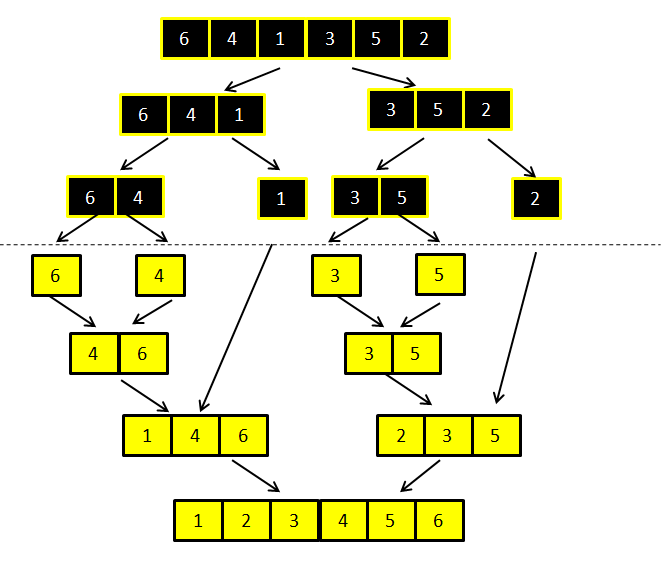
3.3.2 source code of top-down merging and sorting

/**
 * Unified interface definition of integer array sorting
 *
 * @author zhuhuix
 * @date 2020-06-06
 */
public interface Sort  <T extends Comparable<? super T>> {

    /**
     * Integer sort
     * @param arr Array to sort
     */
   void sort(T[] arr);
}

/**
 * Merge sort
 *
 * @author zhuhuix
 * @date 2020-06-11
 */
public class MergeSort<T extends Comparable<? super T>> implements Sort<T> {
    @Override
    public  void sort(T[] arr) {
        mergeSort(arr,0,arr.length-1);
    }

    private void mergeSort(T[]arr,int l,int r){
    	// Recursive exit condition: until the minimum scale
        if (r-l<=0){
            return;
        }
        // Take the median of the current scale
        int mid = (l+r)/2;
       // Left recursive decomposition of median
        mergeSort(arr,l,mid);
        // Right recursive decomposition of median
        mergeSort(arr,mid+1,r);
        // Sort merge
       if (arr[mid].compareTo(arr[mid + 1]) > 0) {
            merge(arr, l, mid, r);
        }
    }

    private void merge(T[]arr,int l,int mid,int r){
        T[]aux=Arrays.copyOf(arr,r-l+1);
        for (int i = l; i <= r; i++) {
            aux[i - l] = arr[i];
        }
        int i = l, j = mid + 1;
        for (int k = l; k <= r; k++) {

            if (i > mid) {
                arr[k] = aux[j - l];
                j++;
            } else if (j > r) {
                arr[k] = aux[i - l];
                i++;
            } else if (aux[i - l].compareTo(  aux[j - l])<0) {
                arr[k] = aux[i - l];
                i++;
            } else {
                arr[k] = aux[j - l];
                j++;
            }
        }
    }

 }

4, Summary

1. The difficulty of divide and conquer algorithm is "how to divide": each sub problem decomposed must exist independently; for example, when sorting an integer array, it needs to divide from N numbers to 1 number
2. Divide and conquer algorithm usually involves recursive program;
3. In the process of merging small-scale problems into large-scale problems, the divide and conquer algorithm generally needs to open up auxiliary space for processing.